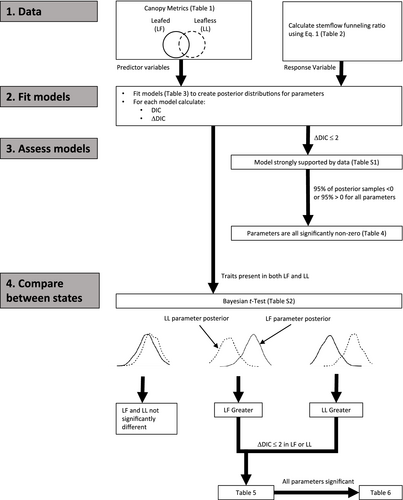
Canopy structure metrics governing stemflow funnelling differ between leafed and leafless states: Insights from a large-scale rainfall simulator
Abstract
An increasing number of studies have examined the effects of various biotic and abiotic factors on stemflow production. Of those that have ascribed the importance of canopy structure to stemflow production, there has been a bias towards field studies. Coupling Bayesian inference with the NIED (National Research Institute for Earth Science and Disaster Resilience, Tsukuba, Japan) large-scale rainfall simulator, this study leveraged a unique opportunity to control rainfall amounts and intensities to pinpoint the canopy structural metrics that differentially influence stemflow funnelling ratios for three common tree species between leafed and leafless canopy states. For the first time, we examined whether canopy structure metrics exert a static control on stemflow funnelling ratios or whether different elements of canopy structure are more or less important under leafed or leafless states, thereby allowing us to determine if tacit assumptions about the static influence of canopy structure on stemflow production (and funnelling) are valid (or not). Rainfall simulations were conducted at 15, 20, 30, 40, 50, and 100 mm h−1 under both leafed and leafless tree conditions (12 simulations in total) to detect any differential effects on the presence or absence of foliage on stemflow funnelling ratios. For leafed conditions, the highest percentages of best-fitting models (ΔDIC ≤2) indicated that stemflow funnelling ratios were mainly controlled by total dry aboveground biomass (Ball), diameter at breast height (DBH), total dry foliar biomass (Bf), tree height (H), and woody to foliar dry biomass ratio (BR). Whilst for the leafless state, the highest percentages of best-fitting models (ΔDIC ≤2) indicated that total dry branch biomass (Bbr) was relatively dominant as was the interaction effects between crown projection area and species (CPA:species). These results compel us to reject any assumption of a static effect of different elements of canopy structure on stemflow funnelling.
1 INTRODUCTION
The importance of canopy interception to the water balance has been well established at multiple spatial scales, ranging from local (i.e., watersheds) (Carlyle-Moses & Gash, 2011; Helvey, 1967; Iida et al., 2017) to continental (Wallace et al., 2013) to global (Miralles et al., 2010). For example, satellite-derived global estimates of canopy interception loss are notable, ranging from 13% to 22% of incoming rainfall for different forest types (Miralles et al., 2010). In drylands, average canopy interception accounted for 24% of incident rainfall for both trees and shrubs (Magliano et al., 2019), whereas average annual interception loss for a 50-year old Sitka spruce forest in Scotland was 28% of incoming rainfall (Johnson, 1990). Similarly, the routing of water through forest canopies via throughfall and stemflow are a maturing subject of inquiry (Levia et al., 2011; Levia et al., 2020; Yue et al., 2021), with many studies focusing on the influence of various biotic or abiotic factors on throughfall and/or stemflow inputs to illustrate the importance of precipitation redistribution in wooded ecosystems (e.g., Cayuela et al., 2018; Gonzalez-Ollauri et al., 2020; Iida et al., 2017; Levia et al., 2019; Tanaka et al., 2017; Yuan et al., 2016; Zhang, Wang, et al., 2020; Zimmermann et al., 2008). Much has been learned from these earlier works, including the importance of antecedent canopy wetness on throughfall chemistry (Zimmermann et al., 2008), the substantial influence of air mass provenance on particulate fluxes in throughfall and stemflow (Cayuela et al., 2019), and the importance of the length of the antecedent dry period to stemflow funnelling from desert shrubs (Zhang, Wang, et al., 2020).
With specific regard to canopy structure (e.g., branch inclination angle, projected crown area, tree height), stemflow amounts have been long known to be larger for deciduous tree species in the leafless period as opposed to the leafed period (e.g., Frost & Levia, 2014; Helvey & Patric, 1965; Staelens et al., 2011). From a biogeochemical standpoint, even the molar ratios of Ca/Al were lower in stemflow of American beech during the leafed period than the leafless period (Levia, Shiklomanov, et al., 2015). For Fagus sylvatica L. (European beech) saplings, those trees with steeper primary branch angles (39.3 vs. 30.2°), higher branch counts per unit projected crown area, fewer leaves per unit projected crown area, straighter boles, and larger woody to foliar biomass ratios (86.8 vs. 15.1 g g−1) produced the most stemflow (Levia, Michalzik, et al., 2015). Similarly, for three sycamore trees in Scotland, branch angle, leaf number, and stem basal diameter were found to affect stemflow amounts (Gonzalez-Ollauri et al., 2020). Yue et al. (2021) even concluded that relative stemflow inputs were more influenced by plant traits (e.g., crown height: width ratio, basal area) than meteorological conditions. These findings dovetail well with other work by Aboal et al. (1999), Yuan et al. (2019), and Cayuela et al. (2018), amongst others, who have documented the effects of canopy structure on stemflow yield. Nonetheless, a deeper process-based understanding of the hydrologic cycle of forested ecosystems could be gained by utilizing an array of novel environmental sensing technologies as well as open source code in the study of canopy interception, throughfall, and stemflow, as exemplified by Tanaka et al. (2015, 2017) and Gonzalez-Ollauri et al. (2020) who used open source boosted regression trees (BRT) code (Elith et al., 2008) to delve into the relative effects of various abiotic and biotic factors on throughfall and stemflow.
The utilization of environmental sensing technologies for precipitation partitioning studies can range from tree-level accelerometers to measure canopy interception (Selker et al., 2020; van Emmerik et al., 2017) and stemflow collection devices (Turner et al., 2019) to continental scale monitoring networks, such as the Trans-African Hydrometeorological Observatory (TAHMO) (Selker et al., 2020), and large scale rainfall simulators (Levia et al., 2019; Nanko et al., 2008). With specific regard to stemflow, Turner et al. (2019) developed an automated Arduino-based hardware sampling system that enabled precise, high-resolution temporal measurements of stemflow inputs from a small green ash tree. Essentially, beyond the collar device, the sensor package consisted of a wetness sensor and ultrasonic rangefinder to record the start and end of stemflow and to continuously record stemflow volume inputs at 10 s intervals. Moving from tree-scale to plot-scale environmental sensor technologies, the NIED (National Research Institute for Earth Science and Disaster Resilience, Tsukuba, Japan) large-scale rainfall simulator permits researchers to hold rainfall intensities constant, thereby allowing the study of canopy structure on rainfall partitioning. For example, Nanko et al. (2008) found that throughfall drop volume proportions increased as the crown thickness, which is the difference between tree height and the height of the base of the live crown, decreased.
In our specific case utilizing the NIED large-scale rainfall simulator, we sought to examine any difference in the canopy structure metrics that affect stemflow input from three tree species (one deciduous and two coniferous) under leafed and leafless conditions, thereby allowing us the ability to ascribe differences in stemflow funnelling to specific canopy structure metrics. Thus, the primary aim of the present study is to examine whether the effects of specific canopy structure metrics, such as branch inclination angle or projected crown area, on stemflow production and funnelling are constant over time or whether their relative importance differs between leafed and leafless periods. Such an understanding is important since canopy structure metrics are sometimes implicitly assumed to exert the same impact on stemflow regardless of leaf state. Hence, it would be useful to pinpoint and quantify any differences in the relative importance (i.e., frequency of predictor variables) of specific canopy structure metrics between leafed and leafless periods. Knowledge of differential importance of various canopy structure metrics on stemflow funnelling between leafed and leafless periods would permit more accurate estimates of the timing and seasonality of water and solute inputs at the tree base, which is necessary to develop a better understanding of the nature of hot spots in the proximal areas of tree stems, especially when considered in conjunction with tree and stand-scale stemflow funnelling infiltration ratios (Carlyle-Moses et al., 2018; Levia & Germer, 2015) or network modelling of stemflow solute transport (Tucker et al., 2020).
2 MATERIALS AND METHODS
2.1 Rainfall simulator and stemflow measurements
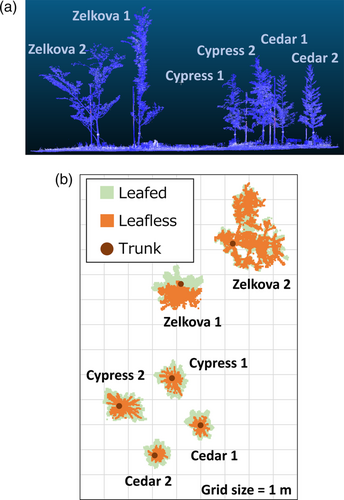
The NIED large-scale rainfall simulator is positioned on a track system so that it can be positioned over five different experimental plots. It has the following dimensions: 76 m length × 49 m wide × 21 m height and is constructed with retractable sidewalls (Nanko et al., 2008). Simulated rainfall is produced from 2176 nozzles at 16 m above the ground to permit falling raindrops to reach the floor at terminal velocity. The rainfall simulator is capable of producing rainfall intensities from 15 to 300 mm h−1 within the entire footprint of the simulator. Six young trees, representing three different tree species and the two most common in Japan (Japanese cedar (Cryptomeria japonica D. Don) and Japanese cypress (Chamaecyparis obtusa [Siebold & Zucc.] Endl.)), were planted within the rainfall simulator as follows: two Japanese cedar, two Japanese cypress and two Japanese zelkova (Zelkova serrata Thunb.). Thus, all six trees experienced the same rain intensity during a set simulation run.
Based on a 3-year record of rainfall measurements in the Tsukuba Experimental Watershed, Japan (Iida et al., 2017), the 10-min and hourly maximum intensity of rainfall was 22.8 mm 10 min−1 (corresponding to 136.9 mm h−1) and 73.5 mm h−1, respectively. Considering natural rainfall conditions, we conducted the rainfall simulations at 15, 20, 30, 40, 50, and 100 mm h−1. The simulation durations were 120 min for experiments with intensities of 15, 20, 30 and 40 mm h−1, and 90 min for 50 and 100 mm h−1. We applied longer duration rains for the lower intensity simulations of 15, 20, 30 and 40 mm h−1 to obtain fully wetted canopies amongst the six trees at the end of each simulation. Rainfall simulations were run once per day and the tree surfaces were permitted to dry for at least 24 h with exposure from the outside since the simulator sidewalls were opened after each experimental run.
To detect any differential effects on the presence or absence of foliage on stemflow funnelling, we carried out the set of rainfall simulations under both leafed and leafless tree conditions (so 12 simulations in total). The experimental trees were manually defoliated at the conclusion of the leafed experimental simulations with the leafless simulations starting immediately thereafter. Since moribund and dead trees remain standing for years in a leafless state, and rates of tree mortality are growing due to biotic attack, climate change, and other mutually interactive stressors (McDowell et al., 2020), we specifically chose to examine the stemflow funnelling from leafless conifers as well as leafless deciduous trees.
We individually collected stemflow from all six trees using a urethane mat affixed to the tree stem at a height of approximately 60 to 70 cm above the ground, and measured stemflow intensity using tipping-bucket flow metres (one tip volume is 50 ml; type KST-50, Uizin Co., Ltd, Tokyo, Japan). The total number of accumulated tips was recorded at 1-min intervals with a datalogger (type CR1000, Campbell Scientific Inc., Logan, Utah). It is recognized that the tipping-bucket flow metres systematically underestimate the inflow of water because the buckets do not capture water during each tip (e.g., Edwards et al., 1974). To correct the systematic biases of measured data of stemflow intensity, we applied the static and dynamic calibration for all tipping-bucket flow metres employed in the experiments (Iida et al., 2012; Iida et al., 2018; Iida et al., 2020).
2.2 Metrics of tree canopy structure
At the conclusion of the rainfall simulations under leafed and leafless conditions, the canopy structure of each tree was assessed and quantified via LiDAR and then destructive sampling once all simulations were completed. We used a ScanStation C10 (Leica Geosystems AG, Heerbrugg, Switzerland) to scan trees. Point cloud data were analysed in R statistical software (version 3.4.1; R Core Team, 2017) with the ‘VoxR’ package version 0.5.1 (e.g., Lecigne et al., 2018) to quantify crown projection area (CPA) for both leafed and leafless tree conditions, crown projection area with foliage (CPALF) and without foliage (CPALL), respectively. The point cloud data was separated into 0.01 m voxels, which is an analogue of a pixel for the two-dimensional images. LiDAR was also used as a cross-cheque of a manual measurements of tree height (H) and trunk lean from the vertical (L). Diameter at tree base (DTB) and diameter of breast height (DBH) were measured using standard diameter tapes. Tree height (H) was measured with a measuring tape, whilst L was measured with a pocket transit. Primary branch count (Nbr) were carefully and manually tabulated and summed. Mean primary branch angle from the horizontal (Abr) was manually determined from transit angle measurements of all primary branches on a tree. The foliar and woody biomass from the destructively sampled experimental trees were oven-dried for 48 h at 80°C. Total dry branch biomass (Bbr), total dry trunk biomass (Btr), total dry woody biomass (Bw), total dry foliar biomass (Bf), total dry aboveground biomass (Ball), and woody to foliar dry biomass ratio (BR) were determined using standard weighing scales.
2.3 Bayesian statistical analysis
| Species | Healthy | DTB | DBH | CPALF | CPALL | H | L | Nbr | Abr | Bbr | Btr | Bw | Bf | Ball | BR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R or M | (cm) | (cm) | (m2) | (m2) | (m) | (°) | (n) | (°) | (g) | (g) | (g) | (g) | (g) | (g g−1) | |
| Cedar1 | R | 5.2 | 2.2 | 0.73 | 0.21 | 2.9 | 3.5 | 44 | 30.6 | 149 | 261 | 410 | 442 | 853 | 0.9 |
| Cedar2 | R | 4.7 | 2.6 | 0.73 | 0.20 | 3.4 | 10.1 | 53 | 36.2 | 125 | 350 | 475 | 464 | 938 | 1.0 |
| Zelkova1 | R | 6.0 | 3.8 | 1.60 | 1.12 | 5.8 | 2.6 | 49 | 45.5 | 556 | 1648 | 2204 | 191 | 2395 | 11.5 |
| Zelkova2 | R | 7.2 | 5.1 | 4.02 | 3.54 | 4.2 | 10.0 | 34 | 37.1 | 1359 | 1839 | 3198 | 277 | 3475 | 11.5 |
| Cypress1 | M | 4.7 | 2.9 | 1.07 | 0.32 | 3.1 | 6.4 | 44 | 22.6 | 163 | 415 | 578 | 957 | 1535 | 0.6 |
| Cypress2 | M | 5.8 | 3.8 | 1.47 | 0.56 | 3.5 | 7.1 | 63 | 17.6 | 294 | 769 | 1063 | 1064 | 2128 | 1.0 |
- Abbreviations: Abr, mean angle of primary branches; Ball, total dry aboveground biomass; Bf, total dry foliar biomass; Bbr, total dry branch biomass; Btr, total dry trunk biomass; Bw, total dry woody biomass; BR, woody to foliar dry biomass ratio; CPALF, crown projection area of leafed state; CPALL, crown projection area of leafless state; DBH, diameter at breast height; DTB, diameter at tree base; H, tree height; L, tree lean; Nbr, number of primary branches, M, moribund; R, robust.
Based on the deviance information criterion (DIC; Spiegelhalter et al., 2002), we define the ΔDIC as the absolute difference between the minimum DIC for the given leaf state (i.e., leafed or leafless) and the DIC for each fitted model, such that the best-fit model has a ΔDIC of 0, and less well fitting models have ΔDIC >0 (Levia, Shiklomanov, et al., 2015). Similar to Levia, Shiklomanov, et al., (2015), we determined that a model is more strongly supported by the data compared to the others when ΔDIC is ≤2. Additionally, for the models with ΔDIC values ≤2 we examined if the parameter posteriors were significantly different from zero (i.e., if the 95% credible intervals were either ≤0 or >0).
All Bayesian statistical analyses were performed using R statistical software. Bayesian analyses were carried out by the ‘R2jags’ package version 0.5–7. We set number of Markov chains to 3, the number of total iterations per chain as 100 000, and length of burn as 50 000. The Markov Chain Monte Carlo (MCMC) analyses were confirmed by the potential scale reduction factors for all predictor variables, which are ≤1.1 (e.g., Gelman et al., 2013). Interested readers are referred to Fer (2020) for a comprehensive introduction to Bayesian analyses and their application to forest-water interactions.
To investigate whether any influencing canopy structure metrics differed significantly between leafed and leafless conditions, we conducted Bayesian t-tests on the leafed and leafless posterior distributions of the effect parameters of each metric for each model that had a ΔDIC ≤2 for either the leafed or leafless states (but usually not both states). For example, in the model that had two parameters of CPA and CPA:Cedar, the posteriors of the effect parameters for CPA and CPA:Cedar in the leafed models were compared to those in the leafless models. If over 95% of the differences between the samples of the two posteriors (leafless - leafed) were ≤0, the effect of the metric was determined to be significantly lower for the leafless state than the leafed state (and vice versa). We also examined how often the different canopy structure metrics had greater effects in the leafed than in the leafless states and vice versa in the models that had high explanatory power (i.e., ΔDIC ≤2) in at least one of the states.
3 RESULTS
3.1 Tree metrics
As expected, CPA for individual trees was markedly lower under leafless conditions as compared to leafed conditions (Table 1; Figure 2). The DTB was more or less the same amongst the experimental trees with a range of only 2.5 cm (Table 1). Japanese zelkova had steeper branch inclination angles on average than either Japanese cedar or Japanese cypress (Table 1). Bbr was much larger for zelkova than either coniferous species being more than double in all cases (Table 1). In contrast, Bf was much larger for Japanese cypress than Japanese cedar or zelkova (Table 1). The BR was an order of magnitude higher for zelkova than cedar or cypress (Table 1). In fact, both cedar and cypress had one tree each with woody to foliar dry biomass ratios of <1 and one tree each at unity (Table 1).
3.2 Stemflow volumes and tree-scale funnelling ratios
On the whole, mean stemflow volumes were lowest for Japanese cypress and larger for zelkova and Japanese cedar (Table 2). The overall largest mean stemflow volume was produced by zelkova tree (Zelkova2, 24 114 cm3) and the smallest by Japanese cypress tree (Cypress2, 2861 cm3). For zelkova, mean stemflow volumes were larger for leafless conditions than leafed conditions, whereas the opposite was true for Japanese cedar (Table 2). No clear pattern for stemflow volumes generated were apparent between leafed and leafless conditions for the two Japanese cypress trees (Table 2). The overall tree-scale funnelling ratios were largest for Japanese cedar and smallest for Japanese cypress. Cedar funnelling ratios were 4–5 times larger than the averaged value of cypress trees (Table 2). Japanese cedar had the largest funnelling ratios under leafed conditions, in contrast to Japanese cypress which had the smallest (Table 2). Under leafless conditions, Zelkova2 had the largest mean tree-scale funnelling ratio (181.1) (Table 2). In general, for most trees, a slight increase in stemflow volumes were found with increased rainfall intensity from 50 to 100 mm h−1. However, no discernable species-specific pattern of stemflow volume was evident for most of the rainfall intensities examined (i.e., between 15–40 mm h−1), with individual trees exhibiting different stemflow production responses in relation to rainfall intensities in this range (Table 2).
| Total amount of stemflow at the end of experiments (cm3) | Funnelling ratio | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Condition | Rainfall intensity (mm h−1) | Total amount of rainfall (mm) | Cedar1 | Cedar2 | Zelkova1 | Zelkova2 | Cypress1 | Cypress2 | Cedar1 | Cedar2 | Zelkova1 | Zelkova2 | Cypress1 | Cypress2 |
| Leafed (LF) | 15 | 30 | 1765 | 1770 | 709 | 11 066 | 324 | 1523 | 154.8 | 111.1 | 20.8 | 180.6 | 16.3 | 44.8 |
| Leafed | 20 | 40 | 3013 | 20 792 | 2082 | 12 639 | 787 | 6833 | 198.1 | 979.0 | 45.9 | 154.7 | 29.8 | 150.6 |
| Leafed | 30 | 60 | 8647 | 9688 | 4130 | 18 923 | 2087 | 2260 | 379.1 | 304.1 | 60.7 | 154.4 | 52.7 | 33.2 |
| Leafed | 40 | 80 | 12 680 | 12 655 | 8106 | 28 375 | 4520 | 10 328 | 417.0 | 297.9 | 89.3 | 173.6 | 85.5 | 113.8 |
| Leafed | 50 | 75 | 10 157 | 18 388 | 4445 | 20 558 | 1903 | 6965 | 356.3 | 461.8 | 52.3 | 134.2 | 38.4 | 81.9 |
| Leafed | 100 | 150 | 27 236 | 41 595 | 15 222 | 42 748 | 6902 | 12 994 | 477.7 | 522.3 | 89.5 | 139.5 | 69.7 | 76.4 |
| Mean | 10 583 | 17 481 | 5782 | 22 384 | 2753 | 6817 | 330.5 | 446.0 | 59.8 | 156.2 | 48.7 | 83.4 | ||
| (±1 SD) | 9172 | 13 595 | 5262 | 11 738 | 2500 | 4456 | 126.9 | 298.1 | 26.5 | 18.3 | 25.8 | 43.6 | ||
| Leafless (LL) | 15 | 30 | 523 | 454 | 3104 | 12 581 | 462 | 2789 | 45.9 | 28.5 | 91.2 | 205.3 | 23.3 | 82.0 |
| Leafless | 20 | 40 | 905 | 2329 | 4745 | 14 850 | 833 | 3585 | 59.5 | 109.6 | 104.6 | 181.7 | 31.5 | 79.0 |
| Leafless | 30 | 60 | 2629 | 4264 | 10 245 | 23 902 | 3582 | 6034 | 115.3 | 133.9 | 150.6 | 195.0 | 90.4 | 88.7 |
| Leafless | 40 | 80 | 8410 | 6985 | 12 377 | 34 461 | 5887 | 8877 | 276.5 | 164.5 | 136.4 | 210.9 | 111.4 | 97.8 |
| Leafless | 50 | 75 | 4080 | 6080 | 6676 | 20 692 | 1623 | 3647 | 143.1 | 152.7 | 78.5 | 135.1 | 32.8 | 42.9 |
| Leafless | 100 | 150 | 10 603 | 12 875 | 20 134 | 48 581 | 5430 | 7832 | 186.0 | 161.7 | 118.4 | 158.5 | 54.8 | 46.0 |
| Mean | 4525 | 5497 | 9546 | 25 844 | 2969 | 5460 | 137.7 | 125.2 | 113.3 | 181.1 | 57.4 | 72.7 | ||
| (±1 SD) | 4121 | 4335 | 6219 | 13 552 | 2349 | 2512 | 85.6 | 51.6 | 27.3 | 29.3 | 35.9 | 22.9 | ||
| Overall mean | 7554 | 11 489 | 7664 | 24 114 | 2861 | 6138 | 234.1 | 285.6 | 86.5 | 168.6 | 53.1 | 78.1 | ||
| (±1 SD) | 7481 | 11 476 | 5833 | 12 222 | 2316 | 3521 | 144.2 | 264.0 | 38.0 | 26.7 | 30.1 | 33.7 | ||
3.3 Stemflow Bayesian analyses: Relative influence of canopy structure metrics
Table 3 shows the number of parameters and the total number of models used to predict tree-scale funnelling ratios with and without interactions terms for both leafed and leafless conditions. The inclusion of interaction terms increased the number of combinations to examine the funnelling ratio. All models with ΔDIC ≤2 are given in Table S1. The frequency and percent of occurrence of predictors with ΔDIC ≤2 and that had all effect parameters be significantly non-zero for both leafed and leafless conditions are listed in Table 4. In the leafed state, Ball and DBH appeared the most in the 31 models that best described stemflow funnelling ratios, followed by Bf, H, and BR (Table 4). For the seven models in the leafless state, Bbr and the interaction term CPA:species appeared in the models most frequently (Table 4). Whether in the leafed or leafless state, compared to canopy structure metrics, RI was not an important factor in our simulation experiment, never appearing in a single model (Table 4). Table 4 is noteworthy in that it shows that the Bayesian generalized modelling of stemflow funnelling ratios was different for leafed and leafless conditions. Specifically, the variables most often appearing in models during leafed conditions (most prominently Ball, DBH, Bf, H, and BR) were different than those under leafless conditions (Bbr and CPA:species most frequent) (Table 4).
| Without interaction terms | Including interaction terms | |||
|---|---|---|---|---|
| Leafed condition | Leafless condition | Leafed condition | Leafless condition | |
| Number of parameters | 14 | 11 | 19 | 14 |
| Total models | 16 369 | 2036 | 524 268 | 16 369 |
| Leafed condition: Total 31 models were fitted in ΔDIC ≤2 | ||
|---|---|---|
| Potential parameters | Frequency of appearance | Appearance rate (%) |
| Ball | 16 | 51.6 |
| DBH | 15 | 48.4 |
| Bf | 10 | 32.3 |
| H | 9 | 29.0 |
| BR | 9 | 29.0 |
| CPA | 8 | 25.8 |
| Bbr | 8 | 25.8 |
| L | 7 | 22.6 |
| Nbr | 7 | 22.6 |
| Bw | 7 | 22.6 |
| Abr | 6 | 19.4 |
| Btr | 5 | 16.1 |
| DTB | 4 | 12.9 |
| Abr:species | 1 | 3.2 |
| BR:species | 1 | 3.2 |
| RI | 0 | 0 |
| Leafless condition: total 7 models were fitted in ΔDIC ≤2 | ||
|---|---|---|
| Bbr | 3 | 42.9 |
| CPA:species | 3 | 42.9 |
| DTB | 2 | 28.6 |
| DBH | 2 | 28.6 |
| Nbr | 2 | 28.6 |
| Abr | 2 | 28.6 |
| CPA | 1 | 14.3 |
| H | 1 | 14.3 |
| Btr | 1 | 14.3 |
| Bw | 1 | 14.3 |
| L | 0 | 0 |
| RI | 0 | 0 |
- Abbreviations: Abr, mean angle of primary branches; Ball, total dry aboveground biomass; Bbr, total dry branch biomass; Bf, total dry foliar biomass; Btr, total dry trunk biomass; Bw, total dry woody biomass; BR, woody to foliar dry biomass ratio; CPA, crown projection area; DBH, diameter at breast height; DTB, diameter at tree base; H, tree height; L, tree lean; Nbr, number of primary branches; RI, rainfall intensity. Expressions of :species indicate interaction terms between factors and tree species.
3.4 Bayesian t-test comparison of metric effect parameters between leafed and leafless states
All models compared between leafed and leafless states are given in Table S2. For a subset of best-fitting models (ΔDIC ≤2 in the leafed or leafless states), the number of instances where the effects of canopy structure metrics on stemflow funnelling differed significantly between the two states are given in Table 5. It is important to note that Table 5 does not include all of the models that were included in the Table S1 (which included all models that had ΔDIC ≤2) because not all canopy metrics were measured for both leafless and leafed states and, thus, could not be compared between the two states (Figure 1). In this subset of models, the interaction term between CPA:Cedar always had a greater effect on stemflow funnelling in the leafed state versus leafless state; however, the effect of neither CPA nor CPA:Zelkova differed significantly between states in any of the models (Table 5). Nbr and Abr had a significantly greater effect on stemflow funnelling in the leafless state than the leafed state in the best-fitting models (Table 5). In around half of the best-fitting models that included DBH, it had a significantly greater effect on stemflow funnelling in the leafed condition, but not when CPA:Cedar was also included in the models (Table S2). Additionally, in half of the best-fitting models that included H, it had a significantly greater effect in the leafed state than the leafless state, but showed the opposite effect (leafed < leafless) in two other models (Table S2). It is worth noting that RI was not a significantly greater differentiator of stemflow funnelling in the leafed or leafless states (Table 5). This is perhaps the reason it was not included in any of the better fitting models (Table 4) as compared to the canopy structure metrics, which were found in the best-fitting models. Seven models had ΔDIC ≤2 for either leafed or leafless states and had effects of all included metrics significantly differ between the two states (Table 6).
| Metric (parameter) | Total count | LF greater | LL greater |
|---|---|---|---|
| CPA:Cedar | 30 | 30 | 0 |
| Bbr | 19 | 0 | 6 |
| H | 16 | 8 | 2 |
| Abr | 16 | 0 | 12 |
| Nbr | 16 | 0 | 16 |
| L | 14 | 0 | 2 |
| Btr | 11 | 2 | 0 |
| DBH | 9 | 5 | 0 |
| Bw | 9 | 1 | 0 |
| CPA | 7 | 0 | 0 |
| DTB | 7 | 0 | 2 |
| Abr:Cedar | 6 | 0 | 0 |
| CPA:Zelkova | 4 | 0 | 0 |
| Abr:Zelkova | 3 | 0 | 0 |
| RI | 2 | 0 | 0 |
- Abbreviations: Abr, mean angle of primary branches; Bbr, total dry branch biomass; Btr, total dry trunk biomass; Bw, total dry woody biomass; CPA, crown projection area; DBH, diameter at breast height; H, tree height; L, tree lean; Nbr, number of primary branches; RI, rainfall intensity. Expressions of :Cedar and :Zelkova indicate interaction terms between factors and tree species of Japanese cedar and Japanese zelkova, respectively.
| Metric 1 | Metric 2 | Metric 3 | Metric 4 | β0 | β1 | β2 | β3 | β4 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LF | LL | LF | LL | LF | LL | LF | LL | LF | LL | ||||
| CPA | CPA:Cedar | - | - | 72.41 ± 29.81 | 91.82 ± 10.26 | 39.28 ± 26.81 | 43.23 ± 8.94 | −446.45 ± 72.96 | −102.90 ± 28.98 | - | - | - | - |
| H | Nbr | Abr | - | 187.35 ± 23.57 | 114.49 ± 9.34 | −219.95 ± 36.22 | −14.58 ± 14.48 | 77.12 ± 26.85 | −13.57 ± 10.60 | 224.10 ± 39.57 | 31.13 ± 15.86 | - | - |
| DBH | Nbr | Bbr | - | 187.07 ± 24.96 | 114.55 ± 7.89 | −532.35 ± 108.40 | −121.51 ± 34.50 | 188.57 ± 57.03 | 38.93 ± 17.93 | 556.73 ± 131.25 | 162.13 ± 41.36 | - | - |
| DTB | Abr | Btr | - | 187.23 ± 24.94 | 114.42 ± 8.06 | 195.12 ± 65.50 | 76.26 ± 21.06 | 157.32 ± 34.70 | 42.23 ± 10.82 | −335.54 ± 74.61 | −72.76 ± 23.88 | - | - |
| Nbr | Abr | Bbr | Btr | 186.96 ± 22.89 | 114.50 ± 8.40 | 114.78 ± 38.20 | 13.73 ± 14.25 | 181.02 ± 33.25 | 36.79 ± 12.32 | 312.13 ± 73.99 | 80.55 ± 27.71 | −407.48 ± 70.28 | −67.11 ± 26.34 |
| DTB | DBH | H | L | 187.36 ± 22.66 | 114.30 ± 8.28 | 266.67 ± 66.54 | 101.16 ± 23.96 | −429.47 ± 78.50 | −101.67 ± 28.66 | 85.98 ± 36.00 | 21.98 ± 13.42 | 176.31 ± 34.62 | 36.00 ± 12.79 |
| DBH | L | Nbr | Bbr | 187.26 ± 22.00 | 114.53 ± 8.08 | −507.57 ± 100.25 | −121.68 ± 34.90 | −65.80 ± 24.03 | 1.22 ± 8.56 | 167.60 ± 57.62 | 38.51 ± 18.14 | 500.02 ± 123.01 | 161.80 ± 42.73 |
- Abbreviations: Abr, mean angle of primary branches; Bbr, total dry branch biomass; Btr, total dry trunk biomass; CPA, crown projection area; DBH, diameter at breast height; DTB, diameter at tree base; H, tree height; L, tree lean; Nbr, number of primary branches. Expression of :Cedar indicates interaction term between factor and tree species of Japanese cedar.
4 DISCUSSION
4.1 Stemflow funnelling and experimental findings in a larger context
Canopy structure is known to influence stemflow production and stemflow funnelling ratios (Aboal et al., 1999; Levia & Germer, 2015; Tanaka et al., 2017; Zhang, Levia, et al., 2020). For example, tree size and differences in bark water storage capacity were found to affect stemflow amounts and the timing of stemflow production within individual rain events (Levia et al., 2010). Cayuela et al. (2018) found that tree size, trunk lean, bark water storage capacity and other canopy structural factors all effect stemflow funnelling and stemflow yield. The dramatic shift from higher to lower funnelling ratios for Japanese cypress at 9 years of age was attributed to a change in branching architecture (Murakami, 2009). Tree height and canopy leaf area index (LAI) as well as leaf state (leafed/leafless) were important factors affecting funnelling ratios in teak (Tanaka et al., 2017). Moreover, Levia, Michalzik, et al. (2015) found a strong influence of woody to foliar biomass ratio on stemflow yield from European beech. Further, the amount of stemflow for mature Japanese cedar has been correlated with DBH and crown thickness (Iida et al., 2010), whereas stemflow from deciduous trees in Cambodian dry tropical forests had a linear relationship with crown projection area unshaded by neighbouring trees (Iida et al., 2011). Our findings on the influence of various canopy structural metrics on stemflow production and funnelling ratios are consistent with these prior studies. Table 4 clearly showed that many canopy structure metrics affect the funnelling ratio, and the stemflow funnelling process is not governed by any single specific metric (e.g., Gonzalez-Ollauri et al., 2020; Levia, Michalzik, et al., 2015). For leafed conditions, the funnelling ratio was mainly controlled by Ball, DBH, Bf, H and BR (Table 4). Whilst for the leafless state, the effects by Bbr and the interaction term CPA:species are relatively dominant (Table 4). Rainfall intensity was not a good differentiator of stemflow funnelling between leafed/leafless trees, in contrast to some canopy structure metrics (Table 5). This is probably partly attributable to the variable nature of stemflow generation between 15 and 40 mm h−1 in the simulator and to our minimum RI of 15 mm h−1, which is relatively large compared with natural rainfall conditions and is enough to wet the branch and stem surfaces and expand the stemflow pathway to the tree base (e.g., Dunkerley, 2014; Iida et al., 2017).
The changing frequency in model appearance of any given canopy structure metric on stemflow funnelling between leafless and leafed periods indicates that the influence of specific canopy structure metrics, for example, Nbr and Abr, fluctuate with the presence or absence of foliage. This is a novel finding. This study has definitively shown that canopy metrics that explain stemflow funnelling are not constant throughout the year between leafed and leafless periods, indicating that different metrics account for stemflow funnelling to greater or lesser degrees whether there is foliage on the trees (Table 5). This is to say that the effects of canopy structure on stemflow funnelling are not static and one cannot assume that the influence is constant over time. Indeed, Table 5 highlights the fact that the woody frame of the tree has a greater impact on funnelling ratios in the leafless period than the leafed period with Nbr, Abr, Bbr, and to a lesser extent, L all appearing in more models in the leafless period than the leafed period. In contrast, CPA:Cedar, H, and DBH appeared in more models in the leafed period (Table 5). Lager amounts of stemflow have been reported during leafless (dormant) period as compared to the leafed period (Brown Jr & Barker Jr, 1970; Mużyło et al., 2012; Neal et al., 1991; Staelens et al., 2008). In the case of dryland shrubs in China, however, Yuan et al. (2017) found that stemflow amount was larger in the leafless period than the leafed period for one shrub species but not another. No significant differences in stemflow amounts were reported between leafed and leafless periods for other shrub species in the Chihuahuan desert of North America (Martinez-Meza & Whitford, 1996). The findings derived from this study indicate that unsheltered branches play a dominant role in stemflow funnelling in the absence of foliage and that the role of the woody frame of the tree is dampened when foliage is present. These results align with findings of Frost and Levia (2014) who found that stressed American beech trees, with fewer leaves than their live, healthy counterparts, had a higher median funnelling ratio (40.4 vs. 34.1) (Frost & Levia, 2014) and Levia, Michalzik, et al. (2015) who found that lower leaf numbers increased stemflow yield for European beech saplings. Gonzalez-Ollauri et al. (2020), however, found that stemflow yield increased with leaf number for three sycamore trees. Regardless of the effect of leaf number on stemflow yield or funnelling, based on our Bayesian analysis, we conclude that any implicit assumption that canopy structure metrics are equally important throughout the year should be rejected, especially for trees whose leaf status changes due to annual senescence and subsequent leaf fall, biotic attack, or any other stressor.
The results of this study have implications for stemflow-soil interactions as the overall mean funnelling ratios range from 53.1 to 285.6 for Cypress1 and Cedar2, respectively (Table 2). For example, working with European beech and sycamore maple, Tischer et al. (2020) found that the both the routing of stemflow on the tree trunk and its infiltration at the trunk base were spatially heterogeneous. Moreover, in conjunction with many other studies (Carlyle-Moses et al., 2020 and those cited therein), they reported that stemflow infiltration areas into the soil were small, with maximum areas ranging from 0.04144 m2 for maple and 0.02262 m2 at the soil surface for beech (Tischer et al., 2020). These areas were found to be even smaller in the mineral soil than the surface with the areas for maple and beech decreasing to 0.03696 and 0.02002 m2, respectively (Tischer et al., 2020). Similar to findings by Spencer and van Meerveld (2016) and Guo et al. (2020), they observed preferential flow of stemflow along coarse roots. Thus, our results which demonstrate the efficient funnelling of stemflow on the aboveground vegetative surfaces along with the findings of these studies support the double-funnelling concept of Johnson and Lehmann (2006) that has been observed for some shrub species in drier regions (Li et al., 2009).
4.2 Limitations of the large-scale rainfall simulator and directions for future work
This study was able to isolate the effects of canopy structure on stemflow funnelling due to the control of rainfall intensity within the rainfall simulator. Whilst there are differences between natural rainfall and simulated rainfall, the simulated rates of rainfall and the control over rainfall intensity has permitted some useful insights into stemflow funnelling in relation to leaf state and other canopy structure metrics. Nonetheless, a rainfall simulator is an artificial environment and the experimental trees were not subject to the solar radiation inputs and winds that can affect evaporative losses from vegetative surfaces in forests. Per the study objectives, the experimental trees were isolated and their crowns did not overlap so that differences in stemflow funnelling could be attributed to the canopy structures of specific trees. It is unclear how the study results might change for trees with overlapping crowns. These differences, in addition to the artificial rainfall, need to be kept in mind when interpreting our results. Finally, one should be cognizant of our relatively small sample size, which was partly due to tree spacing within the rainfall simulator as well as the manual labour needed for defoliation.
Future work should be extended to other tree species to examine whether the findings in this study hold for other species. Since deciduous trees go through leafless, leafing/emergence, full growth, and senescence phenophases, and the biophysical properties of foliar surfaces (e.g., surface microrelief) can change with phenophase (Campellone et al., 2020), future work could examine stemflow funnelling during emergence and senescence as well. Finally, given the increased stress to many coniferous tree species, such as mountain pine beetle (e.g, Hélie et al., 2005), pine wilt disease (e.g., Tamai et al., 2020), and fire (e.g, Mayor et al., 2007), it is likely that the woody crowns of dead leafless coniferous trees can persist in watersheds for years. This is the precise reason as to why this study also examined the stemflow funnelling from leafless conifers (manually defoliated). The leafless coniferous trees facilitated the isolation of the effects of woody structure on stemflow (Mitsudera et al., 1984; Tiedemann et al., 1980; Williams et al., 2019), possibly serving as an analogue for when these trees experience dieback and mortality from stressors. With stress on forests mounting worldwide (Harvey, 2016; Seidl et al., 2017), it is important to begin to establish a database that may be useful in the face of increasing tree mortality.
5 CONCLUSIONS
This study has revealed the most influential canopy structural factors governing stemflow generation under a wide range of rainfall intensities for both leafed and leafless canopy states. For leafed trees, Bayesian analyses demonstrated that the total dry aboveground biomass (Ball) and the diameter at breast height (DBH) appeared the most in the models that best described stemflow funnelling ratios, followed by the total dry foliar biomass (Bf), the tree height (H), and the woody to foliar dry biomass ratio (BR) and, thus, were the most important elements of canopy structure affecting stemflow funnelling. In contrast, the total dry branch biomass (Bbr) and the interaction term between crown projection area and tree species (CPA:species) were the most influential predictors of stemflow funnelling for the leafless state. These results lead to the conclusion that any implicit assumption(s) about a static effect of different elements of canopy structure on stemflow funnelling should be rejected. Moreover, the results of this study can inform the experimental design of future studies which seek to examine the interrelationships amongst canopy phenophase, stemflow funnelling, and the magnified delivery of water and solutes to near-trunk soils.
ACKNOWLEDGEMENTS
D.F.L. and K.N. gratefully acknowledge the support of the Japan Society for Promotion of Science for the award of an Invitation Fellowship for Research in Japan (Ref. No. S16088) that made this study possible. K.I.W. acknowledges support under the United States National Science Foundation Graduate Research Fellowship Program (Ref. No. 1247312). The researchers also recognize Takanori Shimizu, Takafumi Katsushima, and Nathaniel Levia for their assistance with the experiments.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




