Objective assessment of the evolutionary action equation for the fitness effect of missense mutations across CAGI-blinded contests
Contract grant sponsors: National Institutes of Health (GM079656 and GM066099; U41 HG007446 and R13 HG006650); National Science Foundation (DBI-1062455 and CCF-0905536).
For the CAGI Special Issue
Abstract
A major challenge in genome interpretation is to estimate the fitness effect of coding variants of unknown significance (VUS). Labor, limited understanding of protein functions, and lack of assays generally limit direct experimental assessment of VUS, and make robust and accurate computational approaches a necessity. Often, however, algorithms that predict mutational effect disagree among themselves and with experimental data, slowing their adoption for clinical diagnostics. To objectively assess such methods, the Critical Assessment of Genome Interpretation (CAGI) community organizes contests to predict unpublished experimental data, available only to CAGI assessors. We review here the CAGI performance of evolutionary action (EA) predictions of mutational impact. EA models the fitness effect of coding mutations analytically, as a product of the gradient of the fitness landscape times the perturbation size. In practice, these terms are computed from phylogenetic considerations as the functional sensitivity of the mutated site and as the magnitude of amino acid substitution, respectively, and yield the percentage loss of wild-type activity. In five CAGI challenges, EA consistently performed on par or better than sophisticated machine learning approaches. This objective assessment suggests that a simple differential model of evolution can interpret the fitness effect of coding variations, opening diverse clinical applications.
1 INTRODUCTION
Numerous computational methods seek to predict the impact of genetic variations on fitness (Cardoso, Andersen, Herrgård, & Sonnenschein, 2015; Jordan, Ramensky, & Sunyaev, 2010; Katsonis et al., 2014). Most of them focus on protein-coding variants, which are single-nucleotide substitutions that change an amino acid in the encoded protein. Although protein-coding genes only constitute less than 2% of the human genome, it is estimated that they harbor 85% of disease-related mutations (Choi et al., 2009). Several methods rely purely on homology information, estimating whether a given substitution fits with the amino acid differences observed in other species at that same residue position (Choi, Sims, Murphy, Miller, & Chan, 2012; Ng & Henikoff, 2001; Reva, Antipin, & Sander, 2007; Reva, Antipin, & Sander, 2011; Stone & Sidow, 2005). However, the vast majority of the methods also apply machine learning techniques, trained over large datasets and numerous features that may include sequence conservation, functional site information, solvent accessibility, secondary structure, crystallographic B factors, local sequence environment, and intrinsic disorder, among others (Adzhubei et al., 2010; Bromberg & Rost, 2007; Capriotti et al., 2013; Carter et al. 2013; Fariselli, Martelli, Savojardo, & Casadio, 2015; Karchin et al., 2005; Kircher et al., 2014; Li et al., 2009; Liu, Jian, & Boerwinkle, 2011; Niroula et al., 2015; Schwarz et al., 2014; Wei et al., 2013; Yue & Moult, 2006). Although some studies support clinical value (Chan et al., 2007), the performance of these methods is generally mixed with limited agreement to each other (Castellana & Mazza, 2013) and with clinical or experimental data (Flanagan, Patch, & Ellard, 2010; Miosge et al., 2015; Tchernitchko, Goossens, & Wajcman, 2004; Walters-Sen et al. 2015). A common problem, for example, is that performance is sensitive to the availability of sufficient protein homology and structure information (Hicks, Wheeler, Plon, & Kimmel, 2011; Marini, Thomas, & Rine, 2010). A deeper problem is that the integrative modeling of the multiscale impact of a mutation from the protein to the pathway, to the network and on to a cell, a tissue, and an organism appears far too complex for current tools. In search of an alternative approach that focuses on overall fitness effect, we derived an evolutionary action (EA) equation for the fitness effect of coding genetic changes (Katsonis & Lichtarge, 2014). EA is the product between the functional sensitivity (i.e., importance) of the mutated protein sequence position and the size of the mismatch introduced by the amino acid switch. As such, EA requires no specific training. Its performance was evaluated against large mutagenesis study datasets (Katsonis & Lichtarge, 2014), but the CAGI challenges provided a unique opportunity for independent, objective assessment.
The community of Critical Assessment of Genome Interpretation (CAGI) aims to objectively assess computational methods for predicting the phenotypic impact of genomic variations. Until now, CAGI has organized four contests in 2010, 2011, 2013, and 2015 that involved a total of 37 challenges. Only nine of these challenges asked predictors to estimate the fitness effect of single genetic variants and were suited for EA. The rest of the challenges focused on whole-exome sequencing data interpretation of complex traits or on specific tasks that a fitness impact predictor cannot address directly, such as case-control distributions and activity restoration, among others. We applied EA to seven of these fitness effect challenges, as the EA method was unavailable during the first CAGI experiment and a deadline for the NPM-ALK challenge in CAGI 4 was missed. Here, we report on five challenges, after we excluded two. First, the BRCA challenge of CAGI 3 (2013) because the variant classification was not robust, leaving 52 of 62 missense variants (more than 80%) annotated as variants of unknown significance, and then the SCN5A challenge of CAGI 2 (2011) because it only involved three variants, too few to drive conclusions. In order to assess the methods objectively, CAGI assigned independent assessors to each challenge, often from the team that provided the experimental data. Assessors had freedom to choose any assessment tests and strategy. Most often, assessors used multiple tests that evaluate either the rank of the predictions or their proximity to experimental values. Predictions that perform well in tests of the first type may not necessarily perform well in the tests of the other type, and vice versa. Also, there may be tradeoff between some tests, such as between precision and recall (Buckland & Gey, 1994), since the choice of a cutoff may favor performance in one test at the expense of the performance in the other test. Therefore, integrating multiple tests into one overall score has been a common practice in CAGI challenges. Some assessors avoided highlighting one of the methods as the winner, but they rather presented a comprehensive view of the strengths and weaknesses of the submitted methods, often of those with the best performances.
We used our EA method to address CAGI challenges that asked for predictions of the functional and clinical impact of missense mutations. Specifically, we participated in three challenges of CAGI 4 (SUMO ligase, pyruvate kinase, and N-acetyl-glucosaminidase [NAGLU]), in one challenge of CAGI 3 (p16), and one challenge of CAGI 2 (cystathionine beta-synthase [CBS]). In each case, the EA scores ranked the amino acid substitutions by their predicted impact on fitness, so that substitutions with larger fitness changes had high scores (see Methods). Since EA scores have already been shown to correlate with the fraction of deleterious mutations in four different experimental systems (Katsonis & Lichtarge, 2014), these EA scores, here, were treated as the probability of a substitution to be deleterious for the protein function. The final predicted values were modified specifically to match the experimental scales of each challenge with simple linear transformations. This last choice is simple, but potentially introduces errors if the assay sensitivity was nonlinear.
Briefly, the EA method was based on the hypothesis that protein evolution proceeds in infinitesimal fitness steps (Fisher 1930; Orr, 2005) and so can be described by a continuous and differentiable evolutionary function that links genotype and phenotype. If so, a mutation can be viewed as a perturbation of the genotype and its effect on the phenotype should be given by differentiating the evolutionary function. This leads to the action of a single missense mutation as a product of the gradient of the evolution function and the magnitude of the mutation. The gradient can be understood as the sensitivity of a protein sequence position to amino acid substitution, that is, the importance of the genotype position as measured by the evolutionary trace (ET) algorithm (Lichtarge & Wilkins, 2010; Lichtarge, Bourne, & Cohen, 1996; Mihalek, Res, & Lichtarge, 2004). The magnitude of the amino acid change can be approximated with context-dependent log odds. Together, these terms yield the EA scores. Of note, the ET algorithm, aka the gradient of the evolutionary function, has been used in broad applications, such as to identify functional sites and allosteric pathway residues (Yao et al., 2003), guide mutations that block or reprogram function (Rodriguez, Yao, Lichtarge, & Wensel, 2010), and define structural motifs that predict function on large scale (Erdin, Ward, Venner, & Lichtarge, 2010; Ward et al., 2009), such as substrate specificity (Amin, Erdin, Ward, Lua, & Lichtarge, 2013). Also, the use of amino acid substitution log odds is a well-established measure of amino acid similarity (Henikoff & Henikoff, 1992) and its context dependence is well known (Overington, Donnelly, Johnson, Åali, & Blundell, 1992), although a dependence on predicted functional importance was first used in calculating the EA scores (Katsonis & Lichtarge, 2014). In that same study, EA was predictive on large data sets of experimental assays of molecular function, clinical associations with human disease, and population allelic frequency of human polymorphisms, so that the EA equation matched positive controls and was validated across multiple biological scales.
Here, we reviewed the performance of EA on the CAGI challenges. For each challenge, first, we examined qualitatively the relationships between the experimental values and the EA scores by binning the data points according to the experimental or the predicted values. Then, we presented the objective assessments of the CAGI assessors and provided details on what assessment tests were used and whether an overall ranking that weighs multiple tests have been provided by the assessor. Last, for all challenges, we showed the performance of the submissions according to Pearson's correlation coefficient and receiver operating characteristic plots that were performed by the authors in order to compare performance between different challenges. We also calculated these two tests for two well-established methods, PolyPhen2 (Adzhubei et al., 2010) and SIFT (Ng & Henikoff, 2001), as points of reference (details on using these predictors can be found in Methods). Depending on the dataset availability, we also examined whether the submitted predictions performed better on subsets of mutations that had low standard deviation of experimental replicates and therefore higher confidence for the experimental values.
1.1 EA Approach
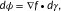 (1)
(1)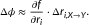 (2)
(2)This is the EA equation, which states that a missense mutation displaces fitness from its equilibrium position by an amount that is proportional to the evolutionary fitness gradient at that site and the magnitude of the amino acid change. Critically, although the function f is unknown, the terms of expression (Equation 2) may nevertheless be approximated from empirical data on protein evolution.
We approximated the evolutionary fitness gradient ∂f/∂ri with the relative importance ranks of the ET method (Lichtarge & Wilkins, 2010; Lichtarge et al., 1996; Mihalek et al., 2004). The gradient represents the displacement of the fitness phenotype for an elementary genotype change. We hypothesized that evolution proceeds in infinitesimal steps (Orr, 2005), so any spontaneous amino acid change in protein evolution is an elementary genotype change that adapts fitness in the genetic and environmental context the protein operates (Coyne & Orr, 1998). We also hypothesized that f is continuous and differentiable, so the gradient equals to the difference in fitness phenotype caused by an elementary genotype change. Together, these two hypotheses suggest that the gradient can be measured by quantifying the correlation of amino acid variation and phylogenetic branching, such as the ET algorithm does (Lichtarge et al., 1996). In the extreme cases, invariant sequence positions yield the maximum evolutionary fitness gradient because any genotypic change can displace fitness beyond any homologous protein, whereas positions that vary even between the closest homologous sequences yield the minimum evolutionary fitness gradient.
To measure the magnitude of a substitution (Δri,X→Y), we used the odds of observing each substitution in homologous proteins (Henikoff & Henikoff, 1992; Overington et al., 1992). For example, the amino acid alanine is substituted to serine more often than to aspartate, in line with greater biophysical and chemical similarities to the former. However, we found that the substitution odds also depend on the evolutionary gradient of the substituted position. For example, the alanine to valine substitution odds form a bell-shaped distribution as the evolutionary gradient at the mutated position varies from maximum to minimum; those of alanine to threonine begin flat and then tail off, whereas those of alanine to aspartate decay steadily (Katsonis & Lichtarge, 2014). Similarly, differences in the substitution odds were found depending on structural features (Overington et al., 1992). Therefore, we approximated Δri,X→Y by substitution odds that depend on the evolutionary importance and on protein structure features of the residue.
2 METHODS
2.1 Calculation of the EA
EA scores were calculated according to the public Web server available for nonprofit use at the URL: mammoth.bcm.tmc.edu/uea, where the human protein name and the amino acid substitution may be used as input. Briefly, the EA Δφ of each mutation was the product of the evolutionary gradient ∂f/∂ri and the perturbation magnitude of the substitution, Δri,X→Y. These two terms, ∂f/∂ri and Δri,X→Y, were measured by percentile ranks of ET scores and of amino acid substitution odds, respectively, as described previously (Katsonis & Lichtarge, 2014). All terms, including the EA scores, have been used in the form of percentile ranks, such that high or low scores indicated high or low impact of the genetic variation, respectively. For example, an EA of 68 implied that the impact was higher than 68% of all possible amino acid substitutions in a protein.
2.2 Calculation of other predictors of mutation impact
SIFT predictions were obtained using “SIFT BLink” (http://sift.jcvi.org/), where we provided the GI number of the query protein. Specifically, we used the GI numbers of 4557415 (CBS), 4502749 (p16), 4507785 (SUMO ligase), 32967597 (pyruvate kinase), and 66346698 (NAGLU). The result was a score between 0 (deleterious) and 1 (neutral) for each possible amino acid substitution within the sequence. SIFT scores were treated as the fraction of the remaining protein function over the wild-type function of the protein (0 means 0% and 1 means 100% function).
PolyPhen2 predictions were obtained using the default parameters (HumDiv classifier) of the batch query tab of PolyPhen2 server (http://genetics.bwh.harvard.edu/pph2/), where we provided the NP identifier of the query protein, the protein residue number, and the wild type and substitute amino acids. We used the NP identifiers of NP_000062 (CBS), NP_000068 (p16), NP_003336 (SUMO ligase), NP_870986 (pyruvate kinase), and NP_000254 (NAGLU). We used the “pph2_prob” value as the prediction score, which ranges between 0 (neutral) and 1 (deleterious), to scale it between 0% and 100% loss of the wild-type function of the protein.
2.3 Statistical tests
2.3.1 Area under the curve of receiver operating characteristic
The area under the curve of the receiver operating characteristic (ROC) plots were calculated using in-house algorithms. The experimental values were transformed to binary values (0 or 1). Typically, the cutoff value was set to 50% of the wild-type protein function, whereas for the p16 challenge we used a cutoff of 75 (experimental values ranged from 50 to 100), as suggested by the bimodal distributions of the experimental values. Multiple cutoffs were also studied when the challenge provided a sufficient number of experimental values of experimental values.
2.3.2 Pearson's correlation coefficient
It was calculated using the built-in function of Microsoft Office Excel.
3 RESULTS
The EA method to estimate the functional and clinical impact of missense mutations was evaluated in five CAGI challenges. In each one, we tested whether the experimental and the predicted values were correlated linearly, or through a more complex dependence, by plotting the average experimental values as a function of the EA scores and the average EA scores as a function of the experimental values. In order to calculate these relationships, we binned the data, often by every 20 or 10 variants when the dataset had more or less than 200 variants. Datasets with less than 20 variants were not binned, whereas coarse binning was used when the experimental values were unevenly distributed. Then, we presented the independent and unbiased assessment of the performance of each submitted prediction, according to the summary of the CAGI assessor. Finally, we presented two widely used statistical tests (the ROC curves and Pearson's correlation coefficient test), as calculated by the authors, in order to provide common ground on comparing performances across different CAGI challenges. We also applied these two tests on predictions from the two most cited mutation impact prediction methods, PolyPhen2 (Adzhubei et al., 2010) and SIFT (Ng & Henikoff, 2001).
3.1 SUMO ligase (CAGI 4 - 2016)
A large library of missense mutations in human SUMO ligase was assessed for competitive growth in a high-throughput yeast-based complementation assay, by the laboratory of Professor F. Roth at University of Toronto (Weile et al., in preparation). The challenge was to predict the effect of mutations on ligase activity, experimentally determined by the change in fractional representation of each mutant clone in the competitive yeast growth assay relative to wild-type clones. Specifically, predictors were asked to submit scores between 0 (no growth) and 1 (wild-type growth) for detrimental mutations, and more than 1 for mutants with better than wild-type growth. Data were divided into three subsets of mutants. Subset 1 contained 219 single amino acid variants, each represented by at least three independent barcoded clones and therefore they were assessed with high accuracy (each barcoded clone represented an individual mutant yeast strain). Subset 2 contained 463 additional single amino acid variants, each represented by fewer than three independent barcoded clones. Subset 3 contained 4,427 alleles corresponding to clones containing two or more amino acid variants.
The EA submission (one prediction attempt) treated EA scores as fitness differences. A priori, these differences were assumed to be mostly detrimental, consistent with the nearly neutral theory of molecular evolution (Ohta, 1992). To account for gain-of-function (GOF) variants, however, we then hypothesized that substitute amino acids seen more often than the wild-type amino acid in the homolog sequences alignment could be beneficial, so we assigned negative (“not detrimental”) sign of EA scores for those variants. Since EA scores vary between 0 (wild type) and 100 (loss of function), the activity of SUMO ligase mutants we submitted to CAGI was: submitEA = 1-EA/100. Next, to combine the effect of multiple mutations (M1, M2, …, MN) on the same allele, we multiplied the effect of each mutation, as: submitEA = (1-EAM1/100)·(1-EAM2/100)·…·(1-EAMN/100). When we plotted the average EA scores for bins of 20 variants with similar experimental growth scores (Fig. 1A), we noted that (1) GOF variants had similar EA scores to variants with nearly wild-type activity, (2) variants with experimental growth score between 0 and 1 showed a good correlation with EA scores, and (3) variants with negative experimental growth scores had lower EA impact than variants with zero growth scores, suggesting that these variants may have some activity against the function measured by the assay. On the other hand, when we plotted the average experimental growth scores for decile bins of EA scores (Fig. 1B), we noted linear correlations for each subset, the best of which was for the subset 1 (R2 = 0.88) that had the highest experimental growth accuracy. This correlation was consistent to the correlations in E. coli lac repressor (Markiewicz, Kleina, Cruz, Ehret, & Miller, 1994), HIV-1 protease (Loeb et al., 1989), and human p53 (Kato et al., 2003) mutations, that were used to validate the performance of EA (Katsonis & Lichtarge, 2014).
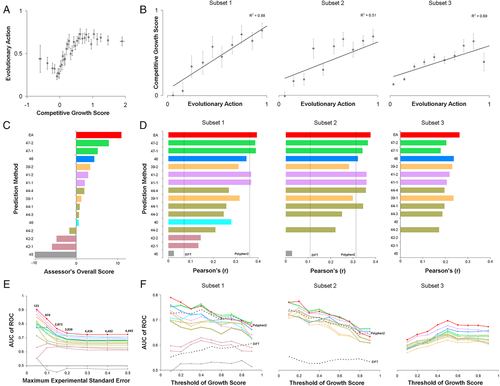
The CAGI assessor for this challenge carefully examined the results by using 18 different assessment metrics to compare the performance of the submissions in each subset. These metrics measured correlations of the experimental growth scores with (1) the original prediction values, (2) the ranks of the predicted values, and (3) a transformation guided by experimental values for the submitted values. Then, as an overall assessment, the CAGI assessor calculated an integrative score for each of these groups of tests and for each data subset, which yielded an overall sum and an overall rank for each method. By this process to define an overall performance score, EA ranked at the top (Fig. 1C). To be clear, the difference between EA and the second best method was small and not necessarily significant. However, all the other methods relied on machine learning and training sets, whereas EA used only the EA equation. Moreover, EA was the only submission with a better overall performance score than a simple conservation-based model developed by the CAGI assessor as a standard of success. To better understand performance, we calculated the Pearson's correlation coefficient and the ROC curves. EA's Pearson's correlation coefficients were only 0.39, 0.38, and 0.26 for the subsets 1, 2, and 3, respectively (Fig. 1D). But these were the best in each data set, including compared with SIFT and PolyPhen2 (which did not participate in the challenge). We note that the area under the ROC curve (AUC) for EA in the three subsets of this challenge was 0.73, 0.72, and 0.70, respectively, for experimental value cutoff of 0.5. These AUC values were also better than the other prediction methods, but they were below the AUC of EA in other datasets (Katsonis & Lichtarge, 2014). To understand this discrepancy, we tested whether the low performance in the ROC metric could be due to experimental uncertainty (Gallion et al., 2017). Indeed, when we restricted the analysis to only account for alleles, in any subset, that had low standard error (SE < 0.05) in the experiments, the AUC rose dramatically, reaching up to AUC of 0.9 (Fig. 1E). We also calculated the AUC of all predictions for nine different thresholds of the growth scores, between 0 and 1. For single mutants, the AUC of most methods increased for low thresholds, suggesting that the computational prediction could separate the partial-function variants from nonfunctional variants better than from the variants with wild-type activity (Fig. 1F). For the multivariant alleles of the subset 3, the cutoff of 0.5 appears to be optimum in separating functional from nonfunctional variants for most submitted predictions.
3.2 Pyruvate kinase (CAGI 4 - 2016)
A large set of amino acid changing mutations of the pyruvate kinase had been assayed in E. coli extracts for their effect on the enzymatic activity and the allosteric regulation of the liver isozyme (L-PYK), by the laboratory of Professor Aron W. Fenton at University of Kansas Medical Center. One subchallenge was to predict the effect of mutations on L-PYK enzyme activity, which was measured as a binary assay result (0, inactive; 1, active). A second subchallenge was to predict the ratios of equilibrium constants for the inhibition of the enzyme by alanine and of the activation of the enzyme by fructose 1,6 bisphosphate. While the first subchallenge is directly relevant to predictions made by EA, addressing the second challenge may require computational analysis beyond the scope of EA. Therefore, here, we focus on predicting the enzymatic activity of L-PYK. Data were split into two experiment subsets: (1) 113 substitutions in nine residue positions, and (2) 430 alanine-scanning mutations.
We used EA to address the enzymatic activity of L-PYK and we submitted one prediction file. EA scores vary between 0 (wild type) and 100 (loss of function), so we treated EA as the probability for a variant to be inactive and we submitted scores calculated as: submitEA = 100-EA. The average activity predicted by EA for active and inactive variants was 30 versus 54 for subset 1 (Mann–Whitney U P value = 7∙10−6) and 34 versus 59 for subset 2 (Mann–Whitney U P value = 10−8), respectively (Fig. 2A). When we binned every 20 mutants with similar EA scores, we noted that variants with EA-predicted activity of more than half of the wild-type activity were active in their vast majority, whereas for the rest bins the fraction of active mutants changed almost linearly with the EA prediction (Fig. 2B). This dependence is similar to that of the T4 lysozyme dataset, which we had attributed to sensitivity of the experimental assay (Katsonis & Lichtarge, 2014).
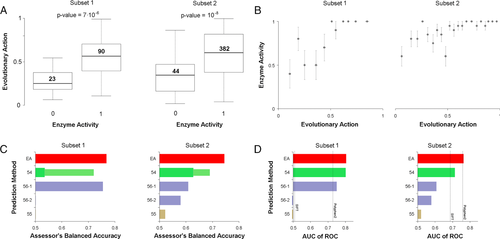
The CAGI assessor of this challenge used the balanced accuracy (BACC) metric to compare the performance of the submitted predictions, for each experimental set. The BACC is given by the average of sensitivity (true-positive rate) and specificity (true-negative rate), which require to set a cutoff for the submitted predictions. The CAGI assessor tested either using as cutoff the value of 0.5, or they calculated the optimum cutoff for each method. For the EA submitted prediction, the value of 0.5 was found to be the optimum cutoff. For each of the two experimental sets, the CAGI assessor found that EA had the top performance according to BACC, even when they optimized the cutoff for the other submitted predictions (Fig. 2C). We reached ourselves the same conclusion when we calculated the AUC of ROC, where EA had AUC of 0.8 and 0.76 in the two subsets, respectively, which were higher than the AUC values of the other submitted predictions as well as of SIFT and PolyPhen2, which did not participate in the challenge (Fig. 2D).
3.3 NAGLU (CAGI 4 - 2016)
The enzymatic activity of NAGLU for 165 missense mutations, which were exclusively found in the ExAC dataset (Lek et al., 2016), was assessed as the percentage of the wild-type NAGLU activity by BioMarin Pharmaceutical, Inc. The challenge was to predict NAGLU activity, submitting scores between 0 (no activity) and 1 (wild-type level of activity), or higher than 1, when the mutation effect was predicted to be detrimental or beneficial. Similar to the pyruvate kinase challenge, we used EA and we submitted one prediction file with scores calculated as: submitEA = 1-EA/100. When we binned every 10 variants with similar enzymatic activity, small enzymatic activities (less than half of the wild type) correlated with the average EA prediction values, but large enzymatic activities (more than half of the wild type) had similar EA scores (Fig. 3A). On the other hand, when we binned every 10 variants with similar EA scores, the average enzymatic activity correlated linearly (R2 = 0.90) with EA scores (Fig. 3B).
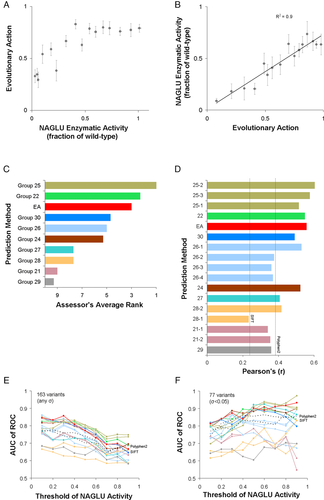
The CAGI assessor of the NAGLU challenge used three tests to compare the performance of the submissions, the root-mean-square deviation (RMSD), the Pearson product-moment correlation coefficient, and the Spearman's rank correlation coefficient. The assessor did not use the well-established ROC test in their overall rank calculation, because they found that the top five submissions, which included EA, had essentially identical performance with AUC values slightly greater than 0.8. In the overall rank, the assessor included only the best performing submission from each predictor group when a group submitted multiple versions, due to redundancy. According to this overall rank, EA had the third best performance (Fig. 3C). The Pearson's correlation coefficient of EA was 0.54, which was the second highest and better than SIFT and PolyPhen2 (Fig. 3D). We also calculated the AUC of ROC for nine different threshold values of the enzymatic activity between 0 and 1 (Fig. 3E). Most predictions had their maximum AUC at small thresholds, where EA did particularly well with AUC of 0.86 for the threshold of enzymatic activity at 0.3, which was the highest AUC value achieved by any prediction method at any cutoff. We also tested the ROC performance when the analysis was limited to variants with small experimental standard deviations (77 variants had SD below 0.05). Indeed, there was improvement in AUC for almost all predictions, but only for large enzymatic activity thresholds, since variants with low enzymatic activity very often had low standard deviations (Fig. 3F). EA reached a maximum AUC of 0.93 for the threshold of enzymatic activity at 0.9, suggesting strong performance when the experimental measurements were very consistent. The facts that no method had consistently the best AUC of ROC at each threshold and that the relative ranks changed when the analysis was restricted to variants with consistent experimental measurements, support the conclusion of the CAGI assessor that the AUC performance was indistinguishable for the top performing methods.
3.4 P16 (CAGI 3 - 2013)
The ability of 10 p16 variants (CDKN2A gene) to block cell proliferation was tested by Maria Chiara Scaini, at Veneto Institute of Oncology of Padova (Scaini et al., 2014). The p16 variants, like the controls of wild-type p16 (negative) and EGFP vector (positive), were expressed in a p16-null-human osteosarcoma cell line and their proliferation rate was recorded for 9 days. The challenge was to predict the proliferation rate of each p16 mutant cell line relative to the positive control, given that the proliferation rate of the wild-type p16 cells was approximately 50% of the proliferation rate of the positive control cells. We used EA to estimate the impact of p16 mutations, and then we predicted that the proliferation rate would be: submitEA = 50+EA/2. Although the correlation of the experimental and predicted values was very strong, with a Pearson's r of 0.84 (Fig. 4A), the formula we used to calculate the proliferation rate from the EA scores was subpar. Setting submitEA = EA would have yielded a much better agreement to the experimentally measured values.
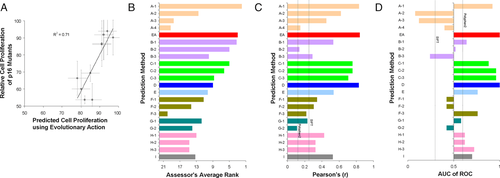
The CAGI assessor of this challenge used four tests to compare the performance of the submitted predictions: Kendall's tau coefficient (τ), RMSD, ROC, and overlap within 10%. The CAGI assessor calculated an overall score from the average rank of these four tests, where EA ranked second out of 22 submissions (Fig. 4B). Of note is that the best submission came from a machine learning method trained with evolutionary and structural features, but the same research group submitted three additional predictions on the same challenge that were trained on different combination of features, and these submissions had intermediate or very poor performance. The EA submission had higher Pearson's correlation coefficient (r = 0.84) than the other submissions and than SIFT and PolyPhen2 (Fig. 4C). Also, the EA submission had perfect ROC, with AUC = 1 in separating the proliferation rate of the variants that had a bimodal distribution (Fig. 4D). The poor performance of SIFT and PolyPhen2 in this challenge was due to predicting maximum impact for almost all of these variants. The best performance of EA on Pearson's coefficient and ROC metrics was consistent between our calculations and the calculations of the CAGI assessor.
3.5 CBS (CAGI 2 - 2011)
The functionality of 84 single amino acid CBS variants, found in homocystinuria patients, was tested in an in vivo yeast complementation assay, by the laboratory of Professor J. Rine, at UC Berkeley. The human CBS clone was expressed and functionally complemented in yeast cells that had the orthologous yeast gene CYS4 removed from the chromosome. In that assay, growth was dependent upon the level of mutant human CBS function, and the rates were expressed as a percentage relative to wild-type (human protein) growth. Two concentrations of pyridoxine, high (400 ng/ml) and low (2 ng/ml), were used. The challenge was to submit predictions on the effect of the variants in the function of CBS in both cofactor concentrations. To address this challenge, we used EA to estimate the loss of CBS activity. At high cofactor concentration, we simply set: submitEA = 100-EA. At low cofactor concentration, we scaled the EA scores to yield lower CBS activities, guided by the test data, such that an EA of 70 will yield 10% CBS activity instead of 30% (linear scaling without changing the extremes, so EA of 0 and 100 will still yield 100% and 0% CBS activity, respectively). Since most CBS variants were found to be experimentally inactive, we binned the variants into those with 0%, 0%–50%, 50%–100%, and more than 100% of the wild-type activity. As expected, the average EA score was higher for the bins of the higher relative growth rate (Fig. 5A). On the other hand, binning every 10 CBS variants by their EA scores yielded strong linear correlations between growth rate and EA (Fig. 5B; R2 was 0.87 and 0.93 for high and low cofactor concentration, respectively).
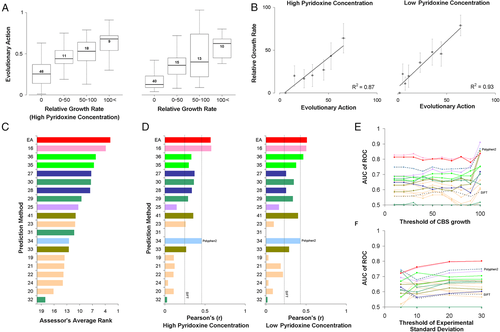
The CAGI assessor of this challenge used nine different tests for each subset of high and low pyridoxine concentration to compare the performance of the submitted predictions, including precision, recall, accuracy, RMSD, Spearman's rank correlation coefficient, F-score, and ROC, among others. Out of 20 submissions, the EA submission had the best performance in nine of the 18 tests, including those of accuracy, RMSD, and F-score, in both datasets. EA was also the best method according to the average rank of all 18 metrics used by the CAGI assessor (Fig. 5C). According to our calculations of the Pearson's correlation coefficients, the EA predictions were the best and the second best method at low and high cofactor concentrations, respectively (Fig. 5D). According to our calculation of the ROC test, EA was the second best method at both cofactor concentrations, with only a marginal difference from the top method (Fig. 5E). When the analysis was restricted to variants with low thresholds of standard deviation, to our surprise, the AUC for almost all predictions dropped, suggesting that lower standard deviations do not imply more accurate experimental measurements in this particular data set (Fig. 5F).
4 DISCUSSION
Following objective assessments across diverse challenges, these data demonstrate that the EA is a robust, state-of-the-art method to estimate the mutational harm of protein-coding variations with consistent tendency to perform best, or nearly so. Out of the five CAGI challenges EA participated in predicting the impact of genetic variations, three times EA was ranked as the top submission as measured by overall score or by the average rank of metrics chosen by the independent CAGI assessors. The other two times, EA ranked as second and third best out of 16 submitted predictions per challenge, on average. Of note, the CAGI challenges were very competitive, with many submissions performing better than PolyPhen2 and SIFT, which are well-known methods, routinely used in the literature to estimate the impact of genetic variations, but which did not participate in the recent CAGI contests. The typical ROC performance of EA was AUC higher than 0.8. An EA AUC below 0.8 seemed to associate with experimental inaccuracies. Conversely, highly accurate experimental data were associated with AUC values above 0.9. This is consistent with the view that experimental gold standards can themselves be fraught with uncertainties, as discussed elsewhere (Gallion et al., 2017).
Whether a method achieves a top ranking or not may often be overinterpreted. Of equal or greater value is whether a method adds orthogonal information and techniques that enrich the domain. In that respect, it is critical to stress that EA is far different from other submissions. It follows a compact and simple mathematical logic, lifted directly from elementary calculus. In so doing it factors in homology and phylogenetic information, explicitly. It sets its parameters (the magnitude of a substitution) over the evolutionary history of all proteins, and reflects the specific protein and residue of interest through the evolutionary gradient, which is computed through a set algorithm and requires no training. Still, EA tended to perform on par or better than most machine learning approaches. These approaches, in contrast to EA, were trained on mutation data, structural stability information, physicochemical properties, and functional site annotation (e.g., known functional motifs, interaction sites, and allosteric sites) in addition to homology data. Moreover, many machine-learning approaches trained to further integrate the combined outputs from many stand-alone mutation impact predictors.
The good performance of the EA equation in CAGI challenges therefore supports the fundamental hypotheses underlying the EA theory. That is, genotype–phenotype evolution in the fitness landscape may be described by a fundamental differential equation, reminiscent of those seen in physics. This is surprising for many reasons. Clearly, the genetic code changes discretely, not smoothly. Also, far from being “infinitesimal,” some mutations bring a heavy toll on patients. More broadly, EA hinges on an evolutionary function f that is never explicitly defined. Lastly, EA is an essentially untrained expression that apparently is unaware of important details, such as a protein's structure, functions, or interactions. Despite this, CAGI objectively shows through its blind contests assessed by independent judges that EA is an effective, accurate, robust, and generally that performs on par or better than sophisticated and powerful statistical and artificial intelligence techniques trained on large data sets.
These apparent paradoxes can be resolved, however, by examining the formal variables EA uses. First, EA models the impact of genetic variations—the central feature of evolution—by applying basic calculus to Sewall's fitness landscape: a mutation causes a fitness displacement equal to the perturbation size times the local fitness sensitivity, that is, the gradient of the mutated position. To estimate this gradient, EA looks at evolutionary history: when this position varied among species, did their fitness change much or little? The answer is taken directly from evolutionary trees, or more accurately from the fundamental equivalence between sequence distances and fitness distance between their species (Lichtarge et al., 1996). Thus, only the evolutionary tree and its record of distances between sequences are needed to estimate f’; f itself is never required. Critically, f’ implicitly accounts for structural, dynamical, functional, and other interaction constraints that guide fitness response to point mutations. Although no statistical training is present, the gradient f’ is specific to each protein and its context. Finally, the EA equation reflects the perturbation on the species, since the evolutionary tree comparisons are between species. As such, a mutation that is deadly to an individual is in fact absent from the evolutionary records of species. By the same token, discrete mutations among individuals become melded into a slow continuous diffusion process along an evolutionary trajectory over geological time scale.
EA currently uses only first-order terms, which were approximated by terms that imply the context. The higher-order terms of the EA equation would account for the epistatic interactions of the residues within a protein or across different proteins, and they may well improve predictions, so residue coupling information would be a valuable improvement in future developments of computing EA (Marks et al., 2011). However, for now, the first differential term of the evolutionary equation by itself has broad practical applications in identifying key functional determinants with which to predict, redesign, or mimic function and specificity (Amin et al., 2013; Rodriguez et al., 2010; Yao et al., 2003). Now, when used as part of the EA equation, it helps interpret the impact of genetic variations to prioritize mutations (Mullany et al., 2015; Rababa'h et al., 2013), assess the quality of exomic data (Koire, Katsonis, & Lichtarge, 2016), stratify head and neck cancer patient outcome (Neskey et al., 2015), and predict their response to treatment (Osman et al., 2015a; Osman et al., 2015b).
In summary, CAGI is an important community exercise that objectively compares and illustrates the relative contribution of diverse methods to interpret mutations. In that light, it appears that the performance of EA is as good on prospective datasets as it was on retrospective datasets (Katsonis & Lichtarge, 2014). Arguably, strengths of the EA approach are its simplicity combined with its generality. That is, EA is not trained, but rather relies on first principles of protein evolution. As such, EA differs profoundly from other CAGI submissions and leading methods to evaluate mutations. Moreover, it is widely applicable to any proteins, since it is impervious to differences between de novo mutations and polymorphisms, to the eukaryotic, prokaryotic, or viral origin of the proteins, and to the enzymatic or multifunctional proteins. As with all homology-based methods, the number and diversity of the available homologous sequences necessary to build a sufficiently deep evolutionary tree remain a limitation, as is the absence, for now, of the second-order terms in the computation of EA. However, the mathematical framework of EA is universal and robustly recognizes the telltale patterns of evolutionary constraints. This robustness, which was shown in the CAGI contests, should make EA, and the associated server, a valuable tool for the functional and clinical interpretation of genetic variations.
Disclosure statement
The authors declare no competing financial interests.




