Longitudinal variability of geomorphic response to floods
Abstract
Morphodynamic response of channels and floodplains to flooding reflects interactions of erosive and resistive forces with sediment transport capacity and supply at multiple scales. Monotonic relationships between reach-scale response to floods with independent variables such as flood stream power and channel confinement can be confounded by longitudinal variations in these variables at longer scales. In these cases, channel response depends on both local and upstream drivers. Using high resolution pre- and post-flood digital elevation models, we calculate reach-scale (0.5 to 1 km) and segment scale (10 km) longitudinal variations in channel widening and sediment balance. We relate these responses to longitudinal variations of unit stream power and channel confinement for selected streams impacted by the 2013 Colorado Front Range regional flood event. These streams transition from steep and relatively confined in the canyons of the foothills to less steep and unconfined on the high plains. The channel widening response is more closely linked with reach scale gradients in unit stream power: abrupt widening typically occurred within reaches where a large drop in unit stream power occurred relative to upstream. Sediment balance followed segment scale trends in unit stream power, exhibiting a net erosional trend within the foothills that switches to a net depositional trend within the transition to the plains. These findings indicate that unit stream power gradients mediate channel response at reach to segment scales. Predictive modeling of stream response to floods and fluvial hazards assessments that only consider absolute values of reach-scale stream power may under-estimate fluvial hazards in some settings by ignoring unit stream power gradients. © 2018 John Wiley & Sons, Ltd.
Introduction
The relationship between magnitude of geomorphic response to floods and the driving and resisting variables that mediate this response has proven challenging to predict in a quantitative manner. Channels and floodplains respond to floods in complex ways involving vertical and lateral erosion and deposition. These processes are mediated by the hydraulic erosivity of the flood event; the erodibility of the channel, floodplain, and valley margins; and the balance between upstream and local sediment supply and transport capacity. Flood erosivity is a function of discharge magnitude, channel and valley slope, and confinement of the channel by the valley margins (Nanson and Croke, 1992). The caliber and cohesivity of the channel and floodplain sediment, the density and character of vegetation along channel banks and floodplain surfaces, and the composition and slope of valley margins all influence erodibility. Erosivity and erodibility both influence the supply of sediment a stream receives and is able to transport downstream during a flood event. Additional sediment contributed to a stream may be derived from uplands via overland flow and debris flows. Longitudinal variability between sediment supply and transport capacity also play a role in geomorphic response to floods (Gartner et al., 2015).
The first predictive frameworks linking geomorphic response with drivers relied upon qualitative relationships with a single hydraulic variable such as total stream power or stream power normalized by channel or valley width: unit stream power (ω) (Graf, 1983; Miller, 1990; Magilligan, 1992; Costa and O'Connor, 1995). With the rise of geospatial information systems and high-resolution data such as digital aerial imagery and LiDAR-derived digital elevation models, additional variables have been identified as mediating geomorphic response to floods. These include channel confinement by valley margins, degree of coupling with hillslopes, channel radius of curvature, and presence of vegetation along the channel among others (Nanson and Croke, 1992; Buraas et al., 2014; Nardi and Rinaldi, 2015; Fryirs et al., 2016). With these new data, more quantitative predictions based on these relationships are now possible. Researchers can evaluate channel response to floods and a host of other variables that mediate it on both larger (Buraas et al., 2014; Rinaldi et al., 2016) and smaller scales (Lea and Legleiter, 2015; Tamminga et al., 2015) than previously possible. This, in turn, allows for large spatial datasets characterizing geomorphic response to floods with the potential for a better understanding of the relationship between geomorphic response to floods and its drivers.
Recent work has been conducted focusing on predicting the location and magnitude of channel response to floods (Aggett and Wilson, 2009; Krapesch et al., 2011; Vocal Ferencevic and Ashmore, 2012; Buraas et al., 2014; Nardi and Rinaldi, 2015; Parker et al., 2015; Yochum et al., 2017) with the aim of better characterizing (i.e. mapping) fluvial hazard zones and informing the management of infrastructure in stream corridors (Piégay et al., 2005; ASFPM, 2016). These studies often rely on ω as a primary variable in predicting channel response metrics like widening, sediment flux, or response severity class. Mechanistic modeling relating hydraulic variables such as ω or bed shear stress at flood discharges to observations of channel response may improve our ability to predict the magnitude and location of flood response (Aggett and Wilson, 2009; Gartner et al., 2015; Tamminga et al., 2015). However, the predictions may be limited at small spatial units of analysis (Lea and Legleiter, 2015; Tamminga et al., 2015). Consideration of appropriate mechanisms and scales is important in predicting channel response to floods and was achieved well by Gartner et al. (2015) who provide a quantitative and mechanistic framework for relating estimates of sediment flux resulting from various flood events to longitudinal variation or gradients in stream power at reach (0.5 to 1 km) and segment (1 to 10 km) scales. Though the linkage between these two variables is presented qualitatively, the patterns are clear and predictable. Sediment flux gradients as a driver of channel adjustment to floods and not just a response is understood to be important, but had not been thoroughly studied due to lack of adequate data.
Other studies have documented that erosive and depositional forms and responses to large flood events correlate with longitudinal variations in ω and channel confinement, defined as the ratio of valley bottom width to channel width. For example, Wohl (1992), Cenderelli and Wohl (2003), Hauer and Habersack (2009), and Thompson and Croke (2013) all found that erosive responses dominated in steeper, confined reaches and depositional responses dominated less confined and milder sloped reaches in both alluvial and bedrock streams. In a hydraulic modeling study, Miller (1995) found that the greatest erosional forces associated with valley morphology occurred at valley expansions. Though not a flood response study, Parker et al. (2015) found that the ratio of up to downstream ω, a metric of ω gradient, predicted erosion- vs deposition-dominated segments at the 1–10 km length scale. Lea and Legleiter (2015) and Tamminga et al. (2015) found weak relationships between ω and channel response to floods at smaller scale units (50 to 100 m), although these studies did not consider relationships over longer scales. In the present study, we evaluate the ability of ω gradient and channel confinement metrics to predict quantitative channel response metrics over reach (~ 1 km) to segment (~ 10 km) scales.
Along with ω, channel confinement by resistant valley or terrace margins has been thought to play a dominant role in channel and floodplain morphology and adjustability (Nanson and Croke, 1992; Brierley and Fryirs, 2005; Fryirs et al., 2016). Channel confinement acts as a primary influence on channel response to floods by limiting lateral adjustment and eliminating or minimizing floodplain presence. Such floodplains distribute flood waters over wider areas, resulting in opportunities for sediment deposition and associated geomorphic response (i.e. channel avulsion, lateral migration, and braiding; Fryirs et al., 2016).
Though broadly transferable methods for quantitative prediction of channel response to flooding are not described in the literature, modeling frameworks and thresholds for predicting channel change have been developed. These include monotonic relationships evaluated with linear regression models to predict continuous response variables, such as channel widening (Krapesch et al., 2011; Nardi and Rinaldi, 2015; Surian et al., 2016); binary categorical response variables modeled using logistic regression (e.g. single thread or braided channel, Bledsoe and Watson, 2001); as well as ordinal thresholds and categorical response variables modeled using a cumulative logit framework (Yochum et al., 2017). Predicting patterns of channel response and predicting qualitative response variables has proven fruitful and can provide actionable results for floodplain management (Gartner et al., 2015; Yochum et al., 2017); however, our ability to quantitatively predict the absolute magnitude of geomorphic response variables remains limited.
- characterize longitudinal patterns of channel response (channel widening and erosion and deposition) at multiple scales, over multiple watersheds and valley types;
- evaluate which driving variables most influence channel response at different scales; and
- identify where within a watershed major channel adjustment can be expected from a flood based on the above relationships.
The result of this study is a semi-mechanistic and semi-quantitative framework for evaluating reach- and segment-scale geomorphic response to floods where sediment supplies during floods and gradients in channel slope and confinement are large.
Data and Methods
Study area
From September 9–16 2013, an exceptional amount of precipitation fell along the Colorado Front Range within a corridor nearly 250 km in length, with periods of high intensity rainfall from September 11–13. Maximum depths greater than 450 mm – in excess of average annual rainfall depths for the region – were recorded over the foothills north of Denver resulting in extreme and widespread flooding in over a dozen stream basins (Gochis et al., 2015). Large flood flow magnitudes and durations resulted in extensive geomorphic work (cf. Costa and O'Connor, 1995). Estimates of peak discharge annual exceedance probabilities in the primary flood-impacted areas ranged from 25% to < 0.5% (25 to > 200-year recurrence intervals, Yochum et al., 2017). Over 1000 debris flows were documented in the foothills (Coe et al., 2014), many of which delivered hillslope debris and sediment directly to flooding creeks and streams to be transported downstream (Anderson et al., 2015; Rathburn et al., 2017). The floods initiated in steep and confined streams within the foothills and transitioned to unconfined settings within the plains downstream. Major geomorphic change within stream corridors resulted, concentrated within the foothills and along the transition to the plains.
Our study area lies within the foothills and high plains along the Colorado Front Range. Upper reaches within the foothills run through canyons composed of granite, granodiorite and biotite gneiss, which transition to partially-confined alluvial valleys set within sandstone and shale formations. These give way to alluvium in the plains (Green, 1992). All study reaches lie downstream of the Front Range ‘knickzone’, a steep region demarking the front of bedrock incision migrating upstream over geologic timescales (Anderson et al., 2006). Downstream of the knickzone, canyon and valley walls are typically steeper than those above the knickzone resulting in a greater susceptibility of landslides and debris flows (Anderson et al., 2015).
We consider the relationship between hydraulic variables describing the erosive power of the floods as well as the reach- to landscape-scale geomorphic setting. We then relate these variables to various metrics measuring physical channel response. These data are collected in a sample of flood-affected watersheds: the Big Thompson River (BT), including a portion of the north fork, Saint Vrain Creek (SV), including the middle and south forks of Saint Vrain Creek, the North Fork of Saint Vrain Creek (NSV), and Left Hand Creek (LH) including James and Little James Creeks (Figure 1, Table 1). Not all watersheds within the footprint of the September 2013 rain event were impacted equally, though our study watersheds contain some of the largest geomorphic changes documented from this event. Within the study area, rainfall was concentrated over the foothills. Discharge peaked near or at the outlet of the canyons to the foothills where the rate of increasing drainage area in the downstream direction begins to decrease and where flood waters are able to spread out over unconfined floodplains and attenuate. The drainage areas of the study reaches range from 20 to 1500 km2 and slopes range from 0.003 to 0.08 m/m. Our study basins are similar to each other in that the study reaches within them begin in steep, confined canyons of the foothills and transition to the unconfined, more mild-sloped reaches of the plains. We begin and end the geographic scope of our analyses based on the extent of available data, which is typically limited by the availability of peak discharge estimates. As such, the upstream and downstream analysis extents vary from watershed to watershed in terms of drainage area and distance downstream from the continental divide.
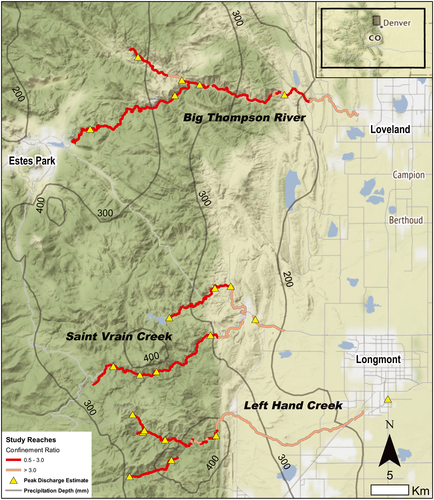
| Watershed | Stream | Length | Number of reaches | Debris flow density | Drainage area | Slope range | Peak discharge | Flood recurrance interval | Unit stream power |
|---|---|---|---|---|---|---|---|---|---|
| (km) | (#/km2) | (km2) | (m/m) | (m3/s) | (yr) | (W/m2) | |||
| Big Thompson R. | N. Fork Big Thompson R. | 8.4 | 15 | 0.04 | 190-220 | 0.01-0.05 | 167-272 | > 100 | 300-6700 |
| Big Thompson R. | 42.6 | 58 | 430-1500 | 0.003-0.065 | 263-538 | 100 | 100-7500 | ||
| St. Vrain Ck. | N. Fork St. Vrain Ck. | 15.0 | 22 | 0.04 | 260-320 | 0.008-0.03 | 283-385 | - | 200-4300 |
| S. Fork St. Vrain Ck. | 22.7 | 41 | 0.50 | 170-240 | 0.01-0.07 | 50-264 | - | 200-8000 | |
| St. Vrain Ck. | 4.2 | 7 | 560-570 | 0.007-0.01 | 699 | >200 | 100-900 | ||
| Left Hand Ck. | James Ck. | 8.8 | 21 | 1.27 | 23-48 | 0.03-0.08 | 51-122 | - | 1000-2900 |
| Left Hand Ck. | 31.9 | 66 | 46-180 | 0.004-0.06 | 38-199 | > 200 | 100-4600 |
We divide the study reaches into two major landscape units (Brierley and Fryirs, 2000): foothills and plains. Foothills reaches tend to be much steeper and more confined than plains reaches. Within the foothills the 1st and 3rd quartiles of reach-averaged slope span 0.02 to 0.036 and those of the confinement ratios (valley floor width/channel top width) span 1.2 to 2.3. Areas of less confinement – floodplain pockets – exist within the foothills, usually at and downstream of major confluences as well as within sharp meander bends within the canyons. Foothills reaches transition to partially confined reaches in alluvial valleys formed within less-resistant sedimentary units. Entering the plains, the 1st and 3rd quartiles of slope for these reaches span 0.007 to 0.013 m/m and those of the confinement ratio span 6 to 29.
Floods along the Front Range below an elevation of approximately 2300 m are dominated by two distinct types of flood events: frequent, less intense snowmelt flooding; and infrequent and intense rainfall-driven floods (Jarrett and Costa, 1988). The latter typically occur in the late summer and fall, though rain-on-snow flood events sometimes occur in the spring. High-intensity, rainfall-driven floods tend to result in greater and more damaging geomorphic change than snow-melt-driven floods but also tend to be more localized. The 2013 flood was an exception to the typically isolated geographic scale of late summer floods and resulted in intense rainfall in many watersheds well above 2300 m in elevation.
Reach delineation
We evaluated geomorphic, hydraulic, and channel response metrics at the reach scale. Reaches were delineated manually and comprise geomorphically-distinct stretches of stream with relatively uniform slope, confinement, and flood response following the concepts of Rinaldi et al. (2013). Reach lengths range from 150 m to 1300 m and average 575 m. Our study includes 230 reaches totaling 133 km in length. Values of all hydraulic and geomorphic variables were assigned to the midpoint of each reach for longitudinal analyses.
We did not include segments of stream that were abutted on both sides by bedrock canyon walls and lacked visible alluvial margins (i.e. non-deformable) as well as reaches in the plains whose response to the flood was altered by substantial floodplain encroachment (such as gravel mining operations). Avulsions, erosion, and deposition responses were substantially influenced in these areas resulting in an incompatibility in reach response between these reaches and those upstream. We did include segments of stream adjoining rip-rapped road embankments in confined reaches that shared the valley floor with roadways. In many cases this rip-rap failed and roadways were washed out, but this bank armoring probably limited lateral channel response in other cases. Small levees and armored banks also existed along some plains reaches. Given the variability in the geographic extent of peak discharge estimates and of the floodplain encroachment along the plains reaches, our analysis extends varying distances from the canyon outlets into the plains for each watershed (10–30 km). Our analysis of NSV ends at the confluence with SV and SV ends at the first gravel pond downstream of this confluence. We end the analysis of BT at the first gravel pond encountered downstream as well. Our analysis of LH extends much further into the plains due to a lack of gravel mining, ending just upstream of where it becomes channelized and enters a fully urbanized area.
Channel confinement
Channel confinement was evaluated by taking the ratio of valley bottom width to pre-flood channel top-of-bank width (Wohl, 2010). Pre-flood top-of-bank widths were sampled for each reach using LiDAR-derived hillshade images and aerial photography. Within the foothills, the majority of reach-scale valley bottom width estimates were generated from a GIS-based tool relying on a 10 m digital elevation model (DEM) (Carlson, 2009). Where this data product was not available, valley bottom width was estimated by identifying the toe of the valley or lowest terrace wall within cross sections cut from pre-flood LiDAR-derived DEMs, which we defined as the ‘valley bottom margin’ (Fryirs et al., 2016). An average of five channel width and valley cross-section measurements were collected for each reach. We defined confined channels as those having confinement ratios ≤ 3, and unconfined channels with ratios > 3. This threshold categorizes semi confined reaches within the foothills (i.e. floodplain pockets) as unconfined. Creating an intermediate confinement category (e.g. 3 < confinement index ≤ 7) did not add to this study as these reaches behaved similarly to those with a confinement index > 7.
Channel confinement largely tracked with landscape unit: confined channels were mostly located within the foothills region, less confined channels in the wider valleys immediately downstream of the canyons in the transition to the plains, and unconfined channels were located within the plains region. Confinement and slope tend to track together as well: average channel slope is greatest for confined channels and is smaller for unconfined channels.
Unit stream power
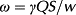 (1)
(1)Channelized flow width was defined by the post-flood width measured between discernable tops of channel banks (i.e. top-of-bank width). Peak discharge values were compiled from several sources by Yochum et al. (2017) using a variety of methods described in Moody (2016). In some cases, multiple independent estimates were co-located for comparison. In cases of disagreement, we chose the estimate that provided for the best continuity of increasing discharge in the downstream direction within the foothills, or decreasing in peak discharge due to floodplain attenuation in the plains (e.g. LH). Peak discharge values were linearly interpolated using distance between two measurements that lacked major intervening tributary inputs. Reaches were excluded from analysis below confluences downstream of which a measurement was lacking. Nevertheless, a high density of peak discharge estimates along the Front Range provided for a continuous set of peak discharge estimates in our study basins (Figure 1).
Channel discharge values were estimated from the total peak discharge values for confined reaches. In unconfined reaches with substantial floodplain flow, the portion of the flow within the channel used to estimate ω was evaluated using a one-dimensional hydraulic model (HEC-RAS v.4.1). Hydraulic models were created from post-flood LiDAR-derived digital elevations models. See Yochum et al. (2017) for more details on the hydraulic modeling methods. A reach averaged slope was calculated using the elevations at the up- and downstream ends of each reach sampled from a pre-flood LiDAR-based DEM. Therefore, reach-scale ω estimates are not based on a uniform length scale as reach lengths are not uniform.
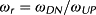 (2)
(2)Erosion and deposition
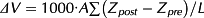 (3)
(3)The sediment balances reported here are not closed because they start at arbitrary locations within each watershed at the upstream-most extent of data availability and do not account for debris flow inputs. Debris flow occurrences over the 2013 flood mapped by Coe et al. (2014) were used to indirectly estimate hillslope sediment supply to the study reaches. Debris flow density per unit watershed area was calculated for each major reach and is reported in Table 1.
Fluvial disturbance width
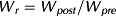 (4)
(4)Statistical analysis
We rely on non-parametric tests of differences in median values of channel response metrics among various groupings of categorical predictor variables due to unequal variances among these groups as well as non-normality. As such, we used the Wilcoxon rank sum test for difference in medians using the base stats package in R (R Core Team, 2016). For comparing more than two groups, we used a non-parametric multiple comparisons test following a Kruskal-Wallis test with a critical p-value of 0.05 using the pgirmess package in R (Siegel and Castellan, 1988; Giraudoux, 2016). Quantile regression of Wr and ωr was performed using the quantreg package in R (Koenker, 2016). Monotonic trend tests were performed using the Kendall τ statistic for heteroscedastic data using the Kendall package (McLeod, 2011).
Results
Longitudinal variability in channel response
In all streams, ω values begin relatively low in the headwaters region reaching a maximum within the middle portion of the foothills (where precipitation maxima were also observed). Unit stream power sharply reduces at the transition from the canyons to alluvial valleys and plains. Large fluctuations in ω are observed within the middle portion of the foothills where steep, confined canyons resulting in local maxima of ω transition to less confined ‘floodplain pockets’ where confinement and slope decrease resulting in local minima of ω. Here, local widening maxima occur at local ω minima or troughs as well as toes in the downstream ω pattern (Figure 2(A) and Figure 3(A), BR at river kilometer (RK) 16, 19, and 27). Toes occur in reaches located at the base of large drops in ω, where ω values remain low in the downstream direction for some distance such as in the transition from the canyons to alluvial valleys and plains (e.g. Figure 3(A), BT at RK 32 and SV at RK 19). Note that the values of all reach-scale variables are plotted at the midpoints of each reach in Figures 3 and 4.
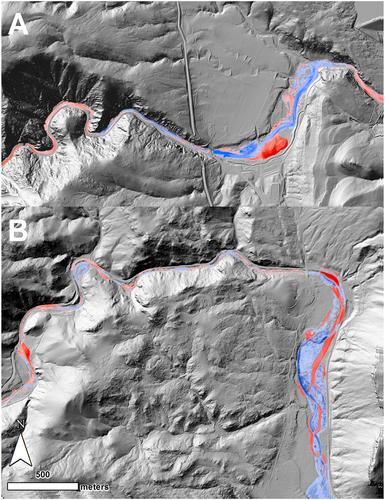
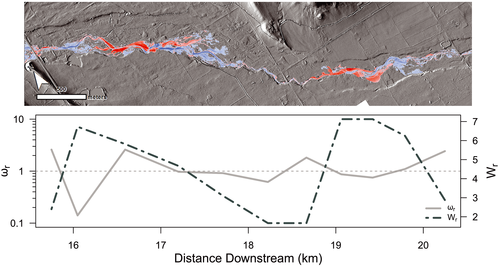
The fluvial disturbance width jumps at the transition from the foothills to the plains where confinement and slope (and hence ω) both decrease concurrently within the transition to less confined valleys (Figures 2(B) and 3(A)). In the transition out of the foothills, these valleys give way to the plains where channels are largely unconfined. In some cases, this jump in channel widening occurs immediately downstream of the outlet of the canyons of the foothills (e.g. BT) denoted as vertical blue lines in Figure 3. In other cases, a lag ranging from 1 to 4 km is observed before a jump in Wr occurs downstream of the canyon outlets (Figure 3(A), NSV, SV, and LH). Elevated Wr values continue downstream for 3 to 8 km before declining again. In the plains region, Wr is high but oscillates from reach to reach due to cycles of channel avulsion and then re-concentration of flow in the original channel (Figure 3, LH, NSV, and SV; Figure 4). In Figure 4, peaks of Wr values coincide or immediately follow troughs in the longitudinal pattern of ωr, which is potentially driven by reach-averaged slope oscillating between approximately 0.02 and 0.01 m/m. Channel confinement by the valley margin does not vary along this particular stream segment.
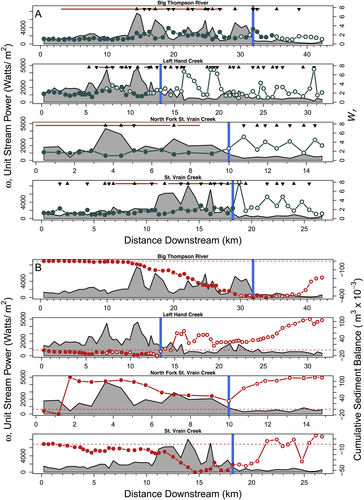
Cumulative sediment balance summed longitudinally shows net degradation within the foothills region transitioning to net aggradation in the plains (Figure 3(B)). Steep negative trends in sediment balance are observed for most streams in the middle reaches within the foothills where precipitation was concentrated, slopes are high, and channels are confined, all of which result in large values of ω. This erosional trend changes to a net depositional trend at the outlet of the canyons and in the transition to the plains where slopes are milder, the channels less confined, and ω reduces compared with the foothills. Channel widening and braiding are often associated with this depositional trend within the first approximately 10 km from the canyon outlets.
Though sediment balance appears more responsive to segment-scale rather than reach-scale patterns in ω, locations of punctuated aggradation are observed at or downstream of substantial decreases in ω (ωr ≪ 1). For example, a large step in net aggradation occurred on LH from kilometers 14–15 after a sharp decrease in ω upstream at kilometers 11–12 (Figure 3(B)). Longer lag distances between these two phenomena are observed on BT and SV, while no lag is observed at NSV. On NSV, rapid rates of sediment deposition continue two to four kilometers downstream and then level off. Note that a sharp increase in sediment volume change occurs within the foothills on NSV (RK 2) where a large quantity of sediment filled a run-of-river diversion dam.
Fluvial disturbance width
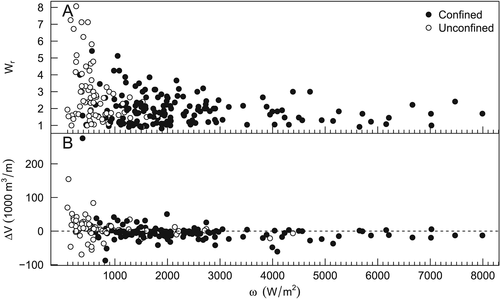
Reach-scale Wr appears to be a decreasing function of ω (Kendall τ = –0.18, p = 3.6E-5), though heteroscedasticity is noted for this relationship (Figure 5). For confined reaches, Wr is not a significant function of ω (τ = –0.09, p = 0.1) and is a weakly significantly decreasing function of ω for unconfined reaches (τ = –0.15, p = 0.05). The negative correlation between Wr and ω is probably related to the largest observed ω values occurring in steep, confined reaches within the foothills where widening was geologically limited. Indeed, nearly 68% of confined reaches by length experienced widening that extended from valley margin to valley margin, which in many cases included the roadway embankments (Figure 3(A) and Figure S3 in Supplemental materials). Noise in these relationships can be explained in part by the influence of stream power gradient (ωr), especially at smaller values of ω for which a wide range of ωr is observed.
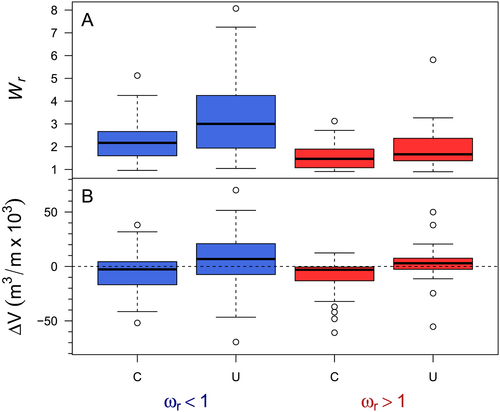
The central tendency of Wr is mediated by ωr and confinement. Confined reaches have a significantly different median Wr value (1.8 ± 0.1, ± one standard error of the median, Table 2) compared with unconfined reaches (2.3 ± 0.3). Unconfined reaches with negative ω gradient exhibit the largest fluvial disturbance width response with a median Wr value of 3.0 ± 0.4 (Table 3). Reaches with negative ω gradients have statistically significant larger Wr, regardless of confinement setting, compared with reaches with positive ω gradients (Figure 6(A), Tables 2 and 3).
| Median Wr | P-value | Median ∆V | P-value | |
|---|---|---|---|---|
| ωr > 1 | 1.6 | 4.4E-09 | –2.1 | 4.0E-03 |
| ωr < 1 | 2.3 | –0.8 | 0.5 | |
| C | 1.8 | 1.3E-05 | –3.0 | 1.8E-05 |
| U | 2.3 | 4.6 | 1.0E-02 |
| Width ratio, Wr | Unit volume change, ∆V | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ω Gradient | ωr > 1 | ωr < 1 | ωr > 1 | ωr < 1 | |||||||
| Confinement | C | U | C | U | C | U | C | U | |||
| Median | 1.5 | 1.7 | 2.2 | 3.0 | Median | -3.0 | 2.9 | -2.7 | 6.8 | ||
| ωr > 1 | C | 1.5 | X | X | –3.0 | X | X | ||||
| U | 1.7 | X | 2.9 | ||||||||
| ωr < 1 | C | 2.2 | –2.7 | X | |||||||
- Note: Median values of Wr and ΔV are provided with units of m/m and m3/m × 103, respectively. X denotes significant differences between pairs.
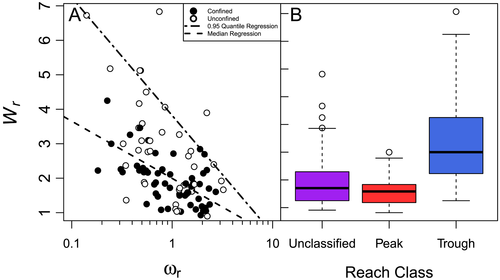
For ωr < 1 (negative ω gradient), much larger and more variable values of Wr exist in the continuous relationship between Wr and ωr (Figure 7(A)). Values of Wr are the highest for reaches with the most negative ω gradients found at troughs or toes in the downstream longitudinal pattern of ω compared with all other reaches (Figure 3(A) and 7(B)). No divergent relationship is observed between Wr and ωr for unconfined versus confined reaches, though the response for unconfined reaches is more variable. Quantile regressions of the relationship between width ratio and the logarithm of ωr evaluated at median and 0.95 quantile values indicate a decreasing relationship. The intercepts for both models are significant (p < 1E-5 for both) and slope is significant for the median regression model (p = 9E-5) but not the 0.95 quantile model (P = 0.14, Figure 7(A)). The 95th quantile regression was performed to quantify an upper envelope of observed width ratio as a function of log10(ωr).
Erosion and deposition
Net erosion and deposition do not vary systematically with absolute values of ω at the reach scale (Figure 5(B)). Reaches with very large values of ω (> 3000 W/m2) are nearly uniformly erosional and reaches with relatively lower values of ω (< 1000 W/m2) exhibit wide ranges of deposition and erosion. Nor is ΔV very sensitive to reach-scale longitudinal variation in ω (Figure 3(B)). Confined reaches tend to be erosional and unconfined reaches depositional regardless of ω gradient (Table 2, Figure 6(B)). This relationship largely reflects the segment scale pattern of net erosion in the foothills, where streams are primarily confined, and net deposition in the plains where streams are primarily unconfined.
Stream power gradient (ωr) more weakly influences ΔV compared with confinement or landscape unit (foothills or plains, Figure 6(B), Tables 2 and 3). The median value of ΔV of reaches with positive gradients is significantly erosional, whereas the median values of ΔV for reaches with negative gradient is not significantly different from zero (Table 3). However, there are notably more confined reaches with positive values of ΔV where ωr < 1 than there are where ωr > 1, indicating that stream power gradient plays a role in sediment erosion and deposition patterns even in confined reaches (Figure 6(B)). As with the widening response, reaches with negative ω gradients result in larger variability in ΔV response. Unconfined reaches with negative ω gradients have the widest spread in ΔV response (including some net erosional values). These reaches also demonstrate greater absolute values of net deposition than unconfined reaches with positive gradients.
There was not a detectable relationship between the fluvial disturbance width and erosion and deposition status at the reach scale. We did not find a significant difference in median widening ratios between net depositional versus net erosional reaches (p = 0.93). Channel widening can result from erosion of the channel margins, a process that dominated in the foothills region, as well as deposition, a process that dominated in the transitional valleys and plains region. The much larger widening ratios observed in the plains occurs as a result of channel avulsion and braiding responses and lack of confinement by valley margins.
Discussion
Drivers and scale of channel response to floods
The fluvial disturbance width and patterns of erosion and deposition are influenced differently by the independent variables studied and their responses occur over different length scales. Of the variables studied, reach-scale Wr is most influenced by ωr followed by confinement, whereas reach-scale ΔV is most influenced by confinement followed by ωr (Figure 6, Tables 2 and 3). Unconfined reaches with negative ω gradients exhibited greater values of Wr and were more depositional than erosional compared with confined reaches with positive ω gradients. Erosion and deposition trends are less sensitive to reach-to-reach variability in ω. Rather, they follow segment-scale trends in ω and confinement from the foothills to the plains with a net erosional trend in the foothills that transitions to a net depositional trend in the plains.
Reach-scale estimates of Wr are sensitive to reach-to-reach scale changes in ω especially at troughs and toes in the longitudinal pattern of ω where negative ω gradients are the strongest and Wr values are the greatest (Figure 7(B), S7). Reach-scale Wr is a decreasing function of ωr; however, much variability exists in this relationship making ωr an imperfect continuous predictor of Wr (Figure 7(A)). Rather, ωr performs well as a categorical covariate used to discriminate between positive and negative ω gradients (Figure 6(A)). The variability in this relationship is reduced when Wr and ωr are evaluated over longer reaches encompassing consistent rising, falling, and constant trends of the longitudinal pattern of ω.
Channel widening via erosional processes (bank erosion and hillslope mass wasting) typically occurred in confined channels with very large values of ω (e.g. Figure 3(A), BT: RK 14–20). The widening response in these reaches was smaller compared with unconfined reaches due to geologic constraints of bedrock and colluvial valley margins. Nevertheless, some 68% of confined reaches by length experienced fluvial disturbance across the entire width of the valley. In some discrete areas the valley was widened due to hillslope failure caused by the flood. Widening due to depositional processes (braiding and avulsion) and channel migration typically occurred for unconfined channels with much lower values of ω (e.g. Figure 3(A), LH: RK 15–20). Regardless of confinement, local maxima in the longitudinal pattern of Wr occurred at troughs or toes of ω where the ω gradient is most strongly negative. The majority of these ω trough and toe reaches were erosional in the foothills and depositional in the plains, following the segment-scale trends of ΔV previously noted (Figure S7).
Erosion of lateral channel margins was the primary source of sediment exported downstream in a study on the NSV upstream of our study area, though debris flows were also important contributors of sediment (Rathburn et al., 2017). Though the longitudinal sediment balances reported in Figure 3(B) are not complete, the surpluses of sediment seen in several streams (LH, NSV, SV) indicate that sediment supplied from hillslopes via debris flows and landslides augmented the supply of sediment in transport beyond what was eroded from channel margins (Anderson et al., 2015). The large coarse sediment loads associated with this flood event played a large role in geomorphic response to the floods within the alluvial valley and plains reaches.
Both the magnitude and gradient of ω are important mediators of channel response. Yochum et al. (2017) presented ω thresholds for categories of geomorphic response to floods (monotonic relationships between channel response and ω) and noted that these apply to segments of stream where channel confinement and ω gradient are relatively uniform. Where substantial transitions of channel confinement and slope exist along a stream, monotonic relationships between ω and channel response tend to not hold. Yochum et al. (2017) did not investigate Wr as an explanatory variable, but rather evaluated geomorphic adjustment based on a semi-quantitative visual assessment of change using ordinal categories of response. Unit stream power peaked in the canyons of the foothills where bedrock and colluvial valley margins confined the channels and limited Wr values. There we documented many reaches in which the fluvial disturbance width extended to the valley margins (Figure S3). These two factors help explain the seemingly decreasing relationship between Wr and ω (Figure 5(A)). Normalizing Wr values by valley width or considering the ratio between valley width and pre- and post-flood channel width might improve the comparison of fluvial disturbance width between confined and unconfined reaches.
The interaction between stream power, stream power gradient, confinement, and channel response to floods has been observed extensively (Wohl, 1992; Cenderelli and Wohl, 2003; Hauer and Habersack, 2009; Thompson and Croke, 2013; Nardi and Rinaldi, 2015; Surian et al., 2016). Nanson and Croke (1992), use confinement along with stream power and grain size as dominant variables in floodplain and disturbance regime classification (i.e. response to floods). By definition, less confined reaches have more degrees of freedom to adjust than confined reaches because less of their length is in contact with resistant valley margins and are therefore more responsive to a variety of disturbances, including floods (Fryirs and Brierley, 2010; Fryirs et al., 2016).
In the companion study, channel confinement ratio and category (i.e. confined and unconfined) were significant predictors of ordinal channel response category (Yochum et al., 2017). There, we found that for a given values of ω, a more severe channel response was generally observed in unconfined vs confined channels. This relationship is observed in the present study as well (Figure 5). Fryirs et al. (2016) distinguish confinement of channels by contact with resistant margins and channel constriction. Both aspects of confinement are at play in channel response in our study. Less resistant boundaries along reaches within the alluvial valleys and plains allowed for a more extreme widening response and a sudden reduction in channel constriction (along with a decrease in slope) resulted in major deposition. Unit stream power gradient integrates how changes in both slope and confinement result in longitudinal changes of channel response.
Qualifications and knowledge gaps
In this study, we focus on metrics of channel confinement and stream power gradient as primary predictors of channel response. We do not emphasize quantitative linkages between the independent and response variables we studied due to the large uncertainty in the relationships (i.e. Figure 7(a)). Rather, we focus on the qualitative patterns and statistically significant differences between response variables and categories of independent variables (Tables 2 and 3). Though statistically significant, much scatter exists in the relationships we report implying that other variables not quantified in this study also play a role in channel response.
Boundary resistance, an important variable in channel response, was not evaluated. The influence of vegetation, bed and bank armoring, and the inherent resistance of boundary materials due to size or composition were also not evaluated. Most similar studies do not explicitly account for boundary resistance either (Surian et al., 2009; Krapesch et al., 2011; Gartner et al., 2015). Nardi and Rinaldi (2015) did consider the influence of percentage of vegetated banks on channel widening. They found that the presence of vegetation did not reduce channel widening response and may have enhanced it in some cases with the hypothesis that flow resistance from vegetation may aid in deposition and avulsion responses during floods. The overall lack of characterization of boundary resistance in flood response studies is a shortcoming of this type of study and reflects the more field intensive nature of defining resistance variables such as bed and material sampling and characterizing vegetation density. Surficial geology maps, which can inform boundary material composition, are readily available though at coarse scales (Green, 1992). Riparian vegetation may also be mapped using remotely-sensed data as in Nardi and Rinaldi (2015), though the limited resolution of these data make them hard to employ for small streams and in confined settings like the foothills of the Colorado Front Range.
Resistant granite and associated colluvium form the lateral boundaries of the majority of confined channels in the foothills (Green, 1992). Pockets of partially-confined reaches contain stores of more erodible alluvium. Moving downstream to the partially-confined alluvial valleys, which are set within sandstone and shale formations along with alluvium, and the plains, dominated by alluvium, lateral resistance to erosion decreases. The increased channel response observed in alluvial valley and plains reaches may in part be due to this reduction in lateral resistance to erosion. The reduction in sediment transport capacity and subsequent deposition of sediment in transport also played a large role in mediating channel response in these areas.
Sediment inputs to the study reaches during the flood include the channel and valley margins, measured in the ΔV calculations, as well debris flows, which were not evaluated. Nevertheless, inputs from debris flows may have influenced channel response at the site of and downstream of these. In a study of 120 debris flows resulting from this flood, Anderson et al. (2015) did not observe widespread evidence of debris fans below debris flow runouts. Rathburn et al. (2017), found that landslides and debris flows on hillslopes accounted for approximately 40% of sediment eroded in the upper North Fork St. Vrain Creek watershed, which is located entirely within the footills, and channel margins contributed the remaining 60%. Nearly 60% of this sediment was delivered to a downstream reservoir and 40% was stored in channel margins that had widened as a result of the flood. Both of these studies indicate that the majority of debris flow supplied sediment was transported downstream during this flood event. We did not find a strong relationship between density of debris flow events and geomorphic response at the scale in which we conducted our observations. Large point inputs of sediment to a stream likely do enhance channel response at the source and for some distance downstream. Debris flows also amplify the volume of runoff as well as its density, potentially increasing the erosive energy of the flood (Kean et al., 2016). The relationship between point sources of sediment from debris flows and channel flood response, as well as the role of sediment flux on channel response is a ripe area for further research.
Finally, we evaluated reach-averaged values of ω based on our manually-delineated, geomorphically-distinct reaches. These reaches did not have uniform lengths because we delineated reaches within relatively homogenous valley types, adjacent land uses, and geomorphic responses to the flood. Elsewhere, ω has been evaluated as a continuously-sampled variable over uniformly-spaced intervals (Gartner et al., 2015; Lea and Legleiter, 2015). Gartner et al. (2015) discuss the importance of choosing an appropriate length scale for smoothing ω values to better discern longitudinal trends. We lumped reaches that were part of segments of continuous longitudinal ω trends (increasing, flat, decreasing) to evaluate how averaging ω and channel responses over longer distances would influence the results. This lumping exercise resulted in largely similar results to not lumping in terms of the longitudinal relationships between channel response metrics and ω (Figure 4) along with the influence of ω gradient and confinement on channel response metrics (Figure 6).
The accuracy of predicting channel response to floods using similar metrics has been demonstrated to increase with the scale of analysis domain. Poor relationships have been observed between channel response metrics and stream power metrics at smaller scales (60 m) (Lea and Legleiter, 2015) and within individual reaches (Tamminga et al., 2015). Clearer relationships were found between stream power gradient metrics averaged over longer reach scales and erosion and deposition responses (100 to 1000 m: Gartner et al., 2015; 1 to 10 km: Parker et al., 2015) and channel widening responses (10 to 50 km: Krapesch et al., 2011). In the present study, the variability in the decreasing relationship between Wr and ωr decreased when variables were averaged over longer reaches within similar increasing, decreasing, and steady longitudinal trends of ω.
Applications
We observed a maximum Wr of 8.0 in the plains and 5.6 in the foothils study. The largest Wr value within the plains occurred in an unconfined reach with relatively mild slope and a strongly negative stream power gradient (Figure 3(A), SV: RK 19, ωr = 0.23). Here, downstream channel migration and avulsion contributed to the large width of disturbance. Channel widening ratio is a decreasing function of ωr, and is typically lower in confined reaches. A wider hazardous zone may exist along reaches with values of ωr that are much lower than unity, low absolute values of ω, and lack of confinement. These reaches are typically located at troughs or toes in the downstream longitudinal pattern of ω, located in floodplain pockets within the foothills and in the alluvial valleys immediately downstream of the foothills within the transition to the plains. However, steep, confined reaches have their own hazards. In many cases Wr was limited by bedrock valley margins and streams widened to occupy the entire, albeit narrow, width of the valley bottom (including paved roads with armored embankments). Nearly 68% of these reaches by length experienced fluvial disturbance that extended across the entire valley (Figures 3(A) and S3). Channel incision and subsequent hillslope mass wasting along with the erosion of channel margins all contribute to highly hazardous fluvial environments in steep, confined reaches.
Large increases in channel widening began zero to four kilometers downstream of the canyon outlets and continued to be high, though oscillatory, for two to eight kilometers downstream. The downstream length of widening response on the Big Thompson River was notably less than the other study reaches. This is likely not explained by a difference in upstream sediment supply as much sediment was eroded from the valley bottom upstream on this stream. Rapid sediment deposition began from zero to eight kilometers downstream of canyon outlets and continued for two to six kilometers. Reach-scale widening and sediment deposition are not coupled as elevated widening typically began closer to canyons outlets and the net depositional trend began further downstream. At the canyon outlets, ω decreased due to milder slope and wider floodplains even though flood discharges generally peaked just upstream and attenuated as the flood moved downstream through the plains. Rainfall was concentrated over the foothills for this flood event. Greater rainfall over the plains might have extended this zone of elevated widening and deposition farther downstream by providing enchanced transport capacity within plains reaches.
In Figure 8, we present a conceptual model of generalized channel response to floods, in terms of Wr and ΔV, as one moves from the foothills to the plains. In the foothills, channel widening and bed incision produce a net erosional response over segment length scales. Channel widening can influence the entire valley bottom in this region, making it highly hazardous, though Wr is smaller in the foothills than in downstream reaches due to channel confinement. Within the alluvial valleys and transition to the plains, Wr increases and the net erosional signal begins to transition to net depositional, often abruptly. Avulsion and braiding dominate the channel response and Wr values peak here. Moving into the plains, net deposition occurs and the widening response diminishes as the coarse sediment load drops out of transport, flood flows spread out over wide valleys, and ω gradients diminish. Note that the downstream extent of elevated Wr values varies greatly among our study streams.

Our study area is a semi-arid environment that receives periodic extreme precipitation events due to the interaction of humid air currents with orographic lift from a mountain range (Gochis et al., 2015). In addition to the hydroclimatology of the region, a sharp transition between steep, confined channels to less steep and unconfined channels from the foothills to the plains results in large gradients in transport capacity over short distances. During the 2013 flood, large quantities of sediment, sourced from debris flows and eroded channel margins were in transport within the steep, confined reaches of the foothills (Anderson et al., 2015; Rathburn et al., 2017). As indicated in our DoD analysis, the increased channel response (i.e. Wr) observed in areas of negative stream power gradient resulted from this sediment load via depositional processes. In terms of predicting the potential for and direction of channel response to floods, our findings may apply to other regions where longitudinal variations of channel confinement and slope interact with one another in similar manners. However, the magnitude of channel response is highly contextual resulting from the interaction of sediment and wood loads during flood events and boundary material resistance.
Reach-scale longitudinal patterns of ω, as well as ω gradient, can be evaluated for a channel network a priori for any frequency of flood using a DEM and a regional regression equation relating flood frequency and magnitude to remotely sensed variables, namely drainage area. Gartner et al. (2015) provide detailed methods for doing so. Channel confinement ratio can be evaluated manually using existing aerial imagery and DEMs. Data products and automated tools for delineating valley bottom width exist (Carlson, 2009; Roux et al., 2015; Gilbert et al., 2016), as well as other definitions of confinement ratio that may influence the relationship between channel confinement and flood response (Fryirs et al., 2016). In sum, the data and tools required to evaluate the variables necessary to determine ω, ωr, and confinement ratio are readily available. These can be used to identify mild-sloped reaches with strongly negative stream power gradients (troughs and toes) as well as steep and confined reaches with elevated values of ω where major geomorphic response to floods can be expected. Quantitative predictions of, for example, Wr, based on similar independent variables are not yet operational given the large variability in response and uncertainty associated with empirical models. However, upper bounds of response may be informative for floodplain management.
Conclusions
We measured channel width change (Wr) and net erosion and deposition (ΔV) at the reach (0.5 to 1 km) and segment scales (10 km) over 133 km of stream in three different basins impacted by the Colorado Front Range flood of 2013. These basins were all similar in that they transition from steep and confined headwaters reaches in the foothills to mild and unconfined mainstem reaches in the plains. This flood transported large sediment loads – sourced from debris flows and channel margins – from the foothills to the plains. We compared channel response metrics to estimates of flood peak unit stream power (ω), the ratio of downstream to upstream reach average ω (ωr), and channel confinement by valley margins to evaluate how these variables influenced channel response. Based on our analysis and observations, we conclude that unit stream power gradient and channel confinement are significant predictors of reach-scale (0.5 to 1 km) and segment-scale (10 km) channel response to floods. However, the great variability in the relationships characterized herein highlights the existence and influence of other factors not incorporated into the present study. These include the inherent resistance of channel and valley margins to erosion as well as the role of vegetation in mediating channel response.
At the reach scale, we found that reductions in unit stream power in the downstream direction, or negative ω gradient (primary) and less channel confinement (secondary) are correlated with increases in the relative fluvial disturbance width. Less channel confinement (primary) and negative ω gradient (secondary) result in a net depositional response; whereas more channel confinement and positive ω gradient result in a net erosional response. However, ΔV was less sensitive to reach-scale ω gradient and followed segment-scale trends of net erosion in the foothills transitioning to net deposition in the plains. The largest channel response in terms of Wr and ΔV occurred in the transition from foothills (steep, confined) to plains (mild, unconfined) with a lag effect of elevated channel response up to 10 km downstream of the outlet of the canyons within the foothills. Spikes in Wr occurred at troughs and toes in the downstream longitudinal pattern of ω where the ω gradient is most strongly negative. There, relatively large widths of fluvial disturbance occurred at relatively low absolute values of ω. Away from these troughs and toes in ω, reach-scale ωr values were less predictive of Wr.
Monotonic relationships between ω and channel response to floods do not apply within stream segments where substantial fluctuations in channel confinement and slope – and hence strongly negative ω gradients – exist. Relying on threshold values of ω, above which dramatic geomorphic response is expected, do not apply in these cases. Rather, consideration of the gradient of ω at the reach and segment scale is important for predicting channel response within these transitions. Future research should work to characterize the role of boundary resistance as well as sediment supply and transport capacity in mediating channel response to floods. Utilizing mechanistic sediment yield and transport models with field-based observational studies of extreme floods will aid in disentangling the complex responses that flood inevitably create.
Acknowledgements
We thank two anonymous reviewers for constructive reviews that substantially improved the manuscript. Discussions with Sara Rathburn and Melissa Foster helped provide geological context to this study. Joel Sholtes and Brian Bledsoe gratefully acknowledge support from the Colorado Water Institute and the Colorado Water Conservation Board as well from a US Forest Service Challenge Cost Share agreement.




