Engineering Reports
Volume 5, Issue 3 e12544
PERSPECTIVE
Open Access

Applying a unified process kinetic equation to advanced materials process analysis: Characterization of the kinetics of isothermal microwave-assisted chemical syntheses

Boon Wong, 

Corresponding Author

Boon Wong

Materials Scientist (Retired), California, USA

Correspondence

Boon Wong, Materials Scientist (Retired), Torrance, CA 90503, USA.

Email: [email protected]

Contribution: Conceptualization (lead), Data curation (lead), Formal analysis (lead), Funding acquisition (lead), ​Investigation (lead), Methodology (lead), Project administration (lead), Resources (lead), Supervision (lead), Validation (lead), Visualization (lead), Writing - original draft (lead), Writing - review & editing (lead)

Search for more papers by this author
First published: 20 June 2022
https://doi.org/10.1002/eng2.12544

Abstract

Rate-enhancement of any isothermal, isobaric chemical synthesis conducted under resonant microwave (RM) irradiation versus the same process activated by conventional field-free heating has been attributed to a reduction in activation enthalpy of the process. This report applies a unified process kinetic equation (UPKE) to demonstrate and characterize non-thermal microwave effects (NTME) on kinetics-enhancements observed in isothermal microwave-assisted chemical syntheses (IMACS). The UPKE, derived from a mesoscopic irreversible thermodynamic model, pinpoints that the rate of any high-affinity chemical reaction is effectively independent of the affinity of the process as described by the mass-action rate law. Energetically, activation enthalpy reduction observed in IMACS is considered the major NTME, which causes dominant process-rate enhancements. This NTME results from RM-induced enthalpy variation during the reaction: RM energy-input first promotes the molar enthalpy of the irradiated reactant(s) at temperature, which consequently motivates an activation enthalpy reduction for rate-enhancement. Conversely, frequency coefficient lowering is another common NTME occurring in IMACS, causing an adverse yet compensable setback to process-kinetics as predicted by the UPKE. Applicability of the UPKE-proposed rationale and methodology for IMACS kinetic characterization is fully confirmed by relevant data in the literature.

1 INTRODUCTION

Since the beginning of this century, microwave-augmented heating has been widely and successfully applied to create novel engineered materials. Compared to conventional heating, this advanced heating technology produces innovative, significantly better-quality materials within much less time at notably lower temperatures.1-8 Initially inspired by the demonstrations of the high novelty and wide-ranging applicability of non-thermal microwave effects (NTME) in materials processing at the first microwave processing symposium sponsored by the Materials Science & Technology (MS&T) Forum in 2009, this author also learned that the underlying science required to guide further development of this novel processing technology was then quite preliminary.9, 10 Since then, numerous rationale and theories of NTME in microwave processing were advanced and refined in the materials community, but with limited applications.11-19 For instance, the conception on ponderomotive action of a microwave-field (MF) may merely provide a rationale of materials transformation/transport enhancements in ionic crystalline solids12-14; while the hypothesis of MF-induced acoustic (hypersound) energy, which augments mass transports and chemical reactions, may only hold for NTME creation in piezoelectric materials.11 Application of the sphere-on-plate sintering-couple model in simulating powdered compact densification motivated by a MF is restricted to a semiquantitative description of the initial-stage densification acceleration of the process in ceramics.15 The theoretical atomistic approach using Heisenberg simulation for dielectric and magnetic materials characterization in microwave heating remains conceptual theoretical work to be completed and validated to engineering use.16 The most recently proposed MF-enhanced surface-charge mobility theory was specifically formulated to comprehend the reactivity and diffusion enhancements of electrically conductive solids in microwave heating.17 While these theories have promoted the understanding of the NTME in microwave materials processing, their validities remain limited to certain specific materials systems and processing conditions.11-19

Using a first-principles approach, this author has been exploring the attribute of NTME, first formulating a unified perspective that incorporates equilibrium thermodynamics, resonant electromagnetics, and classical kinetic theories to comprehend the causes of NTME and their potential influences on materials kinetics in resonant microwave-fields (RMF). Although this unified phenomenological perspective may successfully provide a qualitative rationale of most observed NTME on materials processing enhancements, its assumed equilibrium thermodynamic formalism nature restricts its further quantitative applications onto any real (irreversible) microwave-enhanced process-kinetics analysis.20-25

In order to develop a more realistic methodology that may quantitatively describe any material (matter) transformation or transport process under RMF and field-free conditions, this author recently adopted an irreversible (nonequilibrium) thermodynamic approach to pinpoint and formulate the significance and contribution of NTME to materials energetics and kinetics. Irreversible thermodynamics applies the first principles and methods of thermodynamics to describe energetics and kinetics of transformation/transport processes in systems that are not in overall equilibrium; yet, its formalism is independent of any specific kinetic theory or model. In accordance with irreversible thermodynamics and resonant electromagnetics, this author then derived and published a unified process kinetic equation (UPKE) for isothermal materials processes conducted under field-free, conventional heating and resonant wave-field heating conditions.26-28 The UPKE, derived from a mesoscopic irreversible thermodynamic model accounting for NTME, has been successfully applied to characterize kinetics of both low and high-affinity ceramic processes in the presence or absence of a resonant wave-field.26-28

Since novel chemical syntheses are vital to advanced materials development, this report extends the applications of the UPKE to comprehend and characterize the kinetics-enhancements widely observed in isothermal microwave-assisted chemical syntheses (IMACS). Proposed rationale of microwave-enhanced chemical kinetics suggested by the UPKE is subsequently confirmed with relevant data documented in the literature.

2 UNIFIED PROCESS KINETIC EQUATION (UPKE) – A CRITICAL OVERVIEW

Unified comprehension on isothermal materials process-kinetics stemming from a mesoscopic irreversible thermodynamic model was recently proposed.26-28 This model envisions that kinetically, any materials process should obey Onsager's phenomenological rate law; while energetically, matter transformation or transport occurring during the process should proceed along an activated, Prigogine-type internal coordinate.29-31 The validity of this mesoscopic irreversible thermodynamic model holds for most activated materials processes except for those with an abnormally low energy of activation, that is, processes with an energy barrier less than the product of the gas constant (R) and environmental temperature (T).29 Accordingly, a unified process kinetic equation (UPKE) was derived. Rationale and predictions of this equation not only are highly compatible and consistent with findings inferred by classical kinetic theories of mass transport32, 33 and mass action,29, 31 its applications may also provide a unified comprehension and approach in characterizing isothermal kinetics of most materials processes, either diffusion- or reaction-controlled.26-28

Within the proposed mesoscopic irreversible thermodynamic framework, the steady-state rate of any activated materials process occurring inside a nonequilibrium condensed system, which converts an ideal reacting mixture31, 34, 35 at its initial α-state into a product at the final β-state, may be approximately expressed as26-28
ρ ≈ RT Щ c α δ − 1 × { exp [ − Æ / ( RT ) ] } × { 1 − exp [ − A / ( RT ) ] } = R K × { exp [ − Æ / ( RT ) ] } × c α × { 1 − exp [ − A / ( RT ) ] } = k a × c α × Φ IT , ()
where ρ: global steady-state process-rate (mol m−2 s−1), R: gas constant (8.314 J mol−1 K−1), T: thermodynamic temperature (K), Щ: molar mobility of the reacting species (m mol s−1 N−1), cα: concentration of the ideal reacting mixture at the initial α-state (mol m−3), δ: length of the mesoscopic process path between the initial α-state and the final β-state (m), Æ: activation enthalpy for the isothermal, isobaric materials process (J mol−1), with its magnitude greater than RT – the thermal energy provided by the surroundings, A ≡ −Δrμ = [μ(α)−μ(β)]: affinity (J mol−1), that is, difference between the totaled chemical potentials, μ, at the initial reactant-state, α, and final product-state, β, of the isothermal process, ka ≡ {RTЩδ−1} × {exp[−Æ/(RT)]} = {RK} × {exp[−Æ/(RT)]}: a highly temperature-dependent kinetic factor of the process, containing an activation enthalpy exponential term, {exp[−Æ/(RT)]}, and a pre-exponential frequency coefficient, RK ≡ {RTЩδ−1}, ΦIT ≡ {1−exp[−A/(RT)]}: general driving force of any isothermal materials process—a nonlinear function of the affinity, A, of the process.

Equation (1), the UPKE, predicts that isothermal process-kinetics is generally characterized and controlled by four process parameters: the pre-exponential frequency coefficient, RK, the activation enthalpy, Æ, the initial-state (reactant) concentration, cα, and the affinity, A. Given that both cα > 0 and A ≡ [μ(α)−μ(β)] = −Δrμ > 0 hold for any spontaneous isothermal, isobaric process, the driving force, ΦIT ≡ {1−exp[−A/(RT)]}, for the process is thus positive and finite. Consequently, the forward-process-rate as per Equation (1) is also finite. On the other hand, either when the initial-state (reactant) concentration, cα, or the affinity, A, vanishes, the rate, ρ, in Equation (1) becomes zero, that is, the process stops.

As previously proposed26 and demonstrated in Figure 1, dependence of the isothermal process-rate, ρ, on affinity, A, as per the UPKE, that is, Equation (1), may be practically categorized into three main kinetic domains. Domain 1: near-linear domain, within which ρ is almost linearly proportional to A, as occurring in scenarios of low-affinity processes with [A/(RT)] < 10−2. Domain 2: nonlinear domain, within which the dependence of ρ on A gradually diminishes with increasing A, as occurring in scenarios of medium-affinity processes with [A/(RT)] between 10−2 and 10. Domain 3: independent domain, within which the dependence of ρ on A virtually vanishes, as occurring in scenarios of high-affinity processes with [A/(RT)] > 10. Since kinetics of medium-affinity processes described in Domain 2 is not commonly encountered in daily materials processing, merely the applicability and limitations of the kinetics described in Domain 1 and Domain 3 for materials process characterization are elaborated below.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
A schematic illustrating the UPKE-predicted isothermal process-kinetics as a function of affinity. For practical process characterization, three main kinetic domains are categorized.

2.1 Approximated form of the UPKE for low-affinity (Domain 1) process-kinetics

In scenarios of very low-affinity or near-equilibrium, Domain 1, processes with A/(RT) = [μ(α)−μ(β)]/(RT) < 10−2, for example, solidification/melting, polymorphic transformations, glass-devitrification, precipitate coarsening, grain growth, sintering, high-temperature diffusional creep, and many other diffusion-controlled processes commonly encountered in the materials industry,26-28, 36 their rates could be approximated using Equation (1):
ρ = R K × { exp [ − Æ / ( RT ) ] } × c α × { 1 − exp [ − A / ( RT ) ] } ≈ R K × { exp [ − Æ / ( RT ) ] } × c α × 1 − 1 + AR − 1 T − 1 − AR − 1 T − 1 2 / 2 + AR − 1 T − 1 3 / 6 − ⋯ . $$ {\displaystyle \begin{array}{cc}& \rho =\left\{{}^{\mathrm{R}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{1-\exp \left[-A/(RT)\right]\right\}\\ {}& \kern1.55em \approx \left\{{}^{\mathrm{R}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{1-1+{AR}^{-1}{T}^{-1}-{\left({AR}^{-1}{T}^{-1}\right)}^2/2+{\left({AR}^{-1}{T}^{-1}\right)}^3/6-\cdots \right\}.\end{array}} $$
Since A/(RT) = AR−1T−1 < 10−2 for low-affinity processes, the low-affinity process-rate, Lρ, may practically be written as
L ρ = R K × { exp [ − Æ / ( RT ) ] } × c α × AR − 1 T − 1 = R KR − 1 T − 1 × { exp [ − Æ / ( RT ) ] } × c α × { A } = L K × { exp [ − Æ / ( RT ) ] } × c α × { A } = k l × c α × Φ L , $$ {\displaystyle \begin{array}{cc}& {}^{\mathrm{L}}\rho =\left\{{}^{\mathrm{R}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{{AR}^{-1}{T}^{-1}\right\}\\ {}& \kern1.05em =\left\{{}^{\mathrm{R}}{KR}^{-1}{T}^{-1}\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{A\right\}\\ {}& \kern1.05em =\left\{{}^{\mathrm{L}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{A\right\}={k}_{\mathrm{l}}\times {c}_{\upalpha}\times {\varPhi}_{\mathrm{L}},\end{array}} $$ ()
where kl ≡ {LK} × {exp[−Æ/(RT)]}: temperature-dependent kinetic factor of any low-affinity process, LK ≡ {RKR−1T−1} = {Щδ−1}: pre-exponential frequency coefficient for any low-affinity process, ΦL ≡ A = −Δrμ = [μ(α)−μ(β)]: approximated driving force for low-affinity process-kinetics.

In addition to its exponential dependencies on activation enthalpy and temperature, Equation (2), in the spirit of Fick's law, also predicts that the rate of any low-affinity process is approximately linearly proportional to its affinity. However, the applicability of this approximated form of the UPKE only holds for kinetic analysis of low-affinity processes, for example, a diffusion-controlled process or near-equilibrium (chemical) reaction whose driving force for process-kinetics can be approximated as the affinity of the process. This approximated driving force is, in fact, consistent with the driving force for reactions perceived in classical (equilibrium) thermodynamics.37-43 From the standpoint of either current irreversible-thermodynamic-derived UPKE or recently proposed mass-action (chemical) kinetic expression (see the Appendix), the traditionally perceived driving force for reactions—directly taken as the affinity itself, has validity limitations on kinetic studies of processes particularly with relatively high affinities, that is, processes with A/(RT) > 10−2.

2.2 Degenerate form of the UPKE for high-affinity (Domain 3) process-kinetics

In scenarios of high-affinity, Domain 3, processes with A/(RT) > 10, the term exp[−A/(RT)] in Equation (1) becomes numerically negligible comparing to unity. The UPKE then degenerates and may be simply expressed as
ρ R = R K × { exp [ − Æ / ( RT ) ] } × c α × { 1 − exp [ − A / ( RT ) ] } ≈ R K × { exp [ − Æ / ( RT ) ] } × c α × { 1 − 0 } = R K × { exp [ − Æ / ( RT ) ] } × c α = k a × c α . $$ {\displaystyle \begin{array}{cc}& {}^{\mathrm{R}}\rho =\left\{{}^{\mathrm{R}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{1-\exp \left[-A/(RT)\right]\right\}\\ {}& \kern1.15em \approx \left\{{}^{\mathrm{R}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}\times \left\{1-0\right\}\\ {}& \begin{array}{c}\kern1.15em \\ {}=\left\{{}^{\mathrm{R}}K\right\}\times \left\{\exp \left[-\AE /(RT)\right]\right\}\times \left\{{c}_{\upalpha}\right\}={k}_{\mathrm{a}}\times {c}_{\upalpha}.\end{array}\end{array}} $$ ()
Equation (3) predicts that the rate, Rρ, of any high-affinity process, for example, a reaction-controlled process, is virtually independent of the affinity of the process. Consequently, kinetics of most chemical reactions encountered in the materials industry is solely governed by two properties of the process: (1) the kinetic factor, ka, and (2) the reactant concentration, cα, as in the spirit of the mass-action rate law. On the other hand, the kinetic factor, ka, is a product of the pre-exponential frequency coefficient, RK, and the temperature-activation enthalpy exponential term, {exp[−Æ/(RT)]}, in compliance with the Arrhenius equation.31, 43

3 CHARACTERIZING THE KINETICS OF IMACS USING THE DEGENERATE UPKE

Chemical reactions in condensed state are usually categorized as high-affinity (Domain 3) processes with A/(RT) > 10. Therefore, the degenerate UPKE, that is, Equation (3), may be appropriately applied for an efficient kinetic characterization of most reaction-controlled processes commonly encountered in materials processing. On the other hand, to apply this equation to master chemical kinetics requires quantification of two characteristic parameters of the process: activation enthalpy, Æ, and pre-exponential frequency coefficient, RK.

In the field of microwave-augmented chemistry, rate-enhancements of isothermal chemical (inorganic, organic, or polymeric) syntheses conducted under resonant microwave (RM) irradiation versus their counterpart processes activated by conventional (field-free) heating have been widely recognized. Typical kinetic data obtained from syntheses under both conventional field-free heating and RMF heating conditions are tabulated and compared in Table 1.18, 44-52 Evidently, kinetics-enhancements of chemical reactions conducted under

TABLE 1. Characteristic parameters of typical reaction kinetics measured under field-free and RMF heating conditions
Under field-free Under RMF
Chemical synthesis RKo (s−1) Æo (kJ mol−1) RKRM (s−1) ÆRM (kJ mol−1)
Copper oxide reduction18, 44 > RKRM 328 < RKo 117
Carbon oxidation45 1.6 × 100 118.4 1.1 × 10−3 38.5
Fullerol formation46 5.0 × 103 38.0 1.9 × 10−1 10.5
Ammonium salt synthesis47 2.7 × 104 61.21 2.0 × 102 41.44
Polyamid acid synthesis48 6.6 × 104 46.37 2.2 × 104 38.67
Carvone isomerization49 2.2 × 109 89 3.6 × 108 83
Acrylic acid polymerization50 2.0 × 102 29.5 9.1 × 101 18.6
Epoxy hardening w/amine51 1.1 × 105 48.0 9.0 × 103 44.1
Epoxy hardening w/MHHPA51 1.1 × 107 65.9 2.0 × 105 58.8
Solution imidization52 2.6 × 1010 105 4.4 × 105 57

RMF heating were attributed to a significant reduction in activation enthalpy, Æ, of each individual process. Nonetheless, the pre-exponential frequency coefficients, RKRM, of all syntheses conducted under RMF heating were also reported to be, at various extents, lower than their counterparts, RKo, the pre-exponential frequency coefficients obtained under conventional field-free heating. These two kinetics-related parametric reductions observed under RMF heating in the activation enthalpy and pre-exponential coefficient are considered NTME occurring in chemical reactions conducted under RM irradiation. In order to aptly apply the degenerate UPKE—Equation (3)—to evaluate and characterize the kinetics-enhancements in IMACS, these two NTME must be first comprehended and quantified.

3.1 Reduction in activation enthalpy—The major NTME in IMACS

Energetically, promotion of enthalpy of a chemical system under RM irradiation may not only augment the isothermal thermodynamics (instability) of the system, it may also simultaneously enhance the isothermal kinetics of any macro-process occurring within the affected nonequilibrium chemical body via an activation enthalpy reduction. Figure 2 illustrates the enthalpy variations along the mesoscopic paths of any isothermal chemical reaction under both field-free and RMF heating conditions. As demonstrated in the figure, activation enthalpy of the RM-assisted process is ÆRM = Æo−hF(α), where Æo: activation enthalpy of the field-free heating process, hF(α): initial-state enthalpy gain per mole of the reacting species due to RMF work input. In scenarios of dielectric reactant(s) under RM irradiation, hF(α) is the sum of the time-average, RM-induced polarization and magnetization energy inputs to each mole of the reactant(s), Ω(α) < ∫E(α)dP(α) >RM and Ω(α) < μο∫H(α)dM(α) >RM, respectively, where Ω(α): molar volume of the reactant(s), E(α), H(α): electric and magnetizing fields of the RM irradiation applied onto the reactant(s), respectively, P(α), M(α): resonant polarization and resonant magnetization of the irradiated reactant(s), respectively, μo: permeability of vacuum.26-28 Since hF(α) > 0 under RM irradiation, ÆRM is always lower than its field-free counterpart, Æo. This thermodynamics-based rationalization, therefore, explains and substantiates the occurrence of the major NTME, activation enthalpy reduction, in reactions under RM irradiation as presented in Table 1. Reduction in activation enthalpy will significantly enhance process-kinetics as predicted by the degenerate UPKE, that is, Equation (3).

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
A schematic showing the enthalpy variations along the mesoscopic paths, ξ, of any isothermal chemical reaction under field-free and RMF heating conditions.

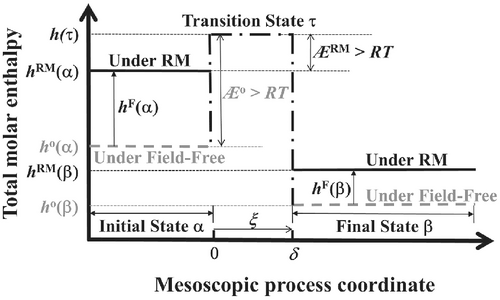
3.2 Decrease in pre-exponential frequency coefficient—Another NTME in IMACS

For a given reactant concentration, cα, the pre-exponential coefficient, RK ≡ {RTЩδ−1}, in the degenerate UPKE dictates the upper limit for the rate of a reaction. From the view of chemical dynamics, magnitude of RK is dominated by Щ, the molar mobility of the reacting species which, in general, governs the molecular collision-attempt frequency of the reacting species during a reaction. Given that in condensed state, vibration is the basic mode of molecular motion, molar mobility, Щ, of the reacting species is thus expected to be proportional to both frequency, ν, and modes, M, of molecular vibration; mathematically, Щ ˜ ν × M, where ˜ denotes “proportional to”.

Under conventional field-free heating, typical magnitude of thermally-induced vibrational frequency of any molecule in a system, νo, within the normal processing temperature range (250 K ≤ T ≤ 2500 K) is from 5 × 1012 Hz to 5 × 1013 Hz as per the Debye-Eyring frequency expression31, 32, 43; its vibrational modes, Mo, particularly for organic molecules, could be multiple: stretching, bending, rocking, wagging, twisting and so forth.53 On the other hand, frequency of molecular vibration under RMF heating is synchronized by the applied RMF frequency in the range of 109 Hz < νRM < 1011 Hz; the vibrational mode, MRM, is usually restricted by the uniform RMF direction as well. From the above molecular dynamic standpoint, one may realize that the molar mobility under RMF heating, ЩRM ˜ (νRM × MRM) < (νo × Mo) ˜ Щo, the molar mobility under conventional field-free heating in any condensed-state reaction at a given temperature.

Consequently, RKRM, which is proportional to ЩRM, is expected to be less than RKo, which is proportional to Щo at temperature. Depending on nature of material and processing condition, RKo of a given chemical synthesis under conventional field-free heating, accordingly, could be up to four to five orders of magnitude higher than its counterpart, RKRM, under RMF heating. This anticipation fully confirms the pre-exponential frequency coefficient measurements obtained from various IMACS studies (Table 1).

3.3 Commentary on IMACS kinetics-enhancements

Originally derived from mesoscopic irreversible thermodynamics, the degenerate UPKE, that is, Equation (3), states that for a given reactant concentration, cα, isothermal reaction kinetics is exponentially related to the activation enthalpy, Æ, and at the same time it is also linearly proportional to the pre-exponential frequency coefficient, RK. Physically, activation enthalpy, Æ, dictates whether the colliding reacting species during reaction have sufficient energy to overcome the required threshold energy barrier for molecular bonding rearrangement to form the product. Accordingly, reduction in Æ of any reaction will result in a remarkable (exponential) population augmentation of the successfully activated reactant-interactions at temperature, thereby greatly increasing the process-rate. In contrast, lowering the RK may also suggest a reduction in frequency and/or possible modes of the reactant collisions during reaction, thus inducing an adverse, but to certain extent compensable setback to the kinetics.

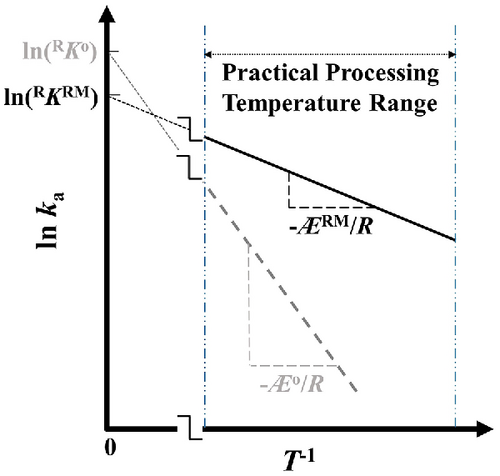
Since most chemical reactions encountered in the materials industry are considered highly-activated processes possessing Æ > > RT, the populations of successful reactant interactions forming products during reaction at nominal processing temperatures are dominantly determined by the Æ-exponential term in Equation (3). For this reason, the enormous (exponentially dependent) impact on kinetics-acceleration in any IMACS caused by the reduced activation enthalpy would far exceed and effectively compensate the relatively minor (linearly dependent) kinetic setback initiated by the decreased pre-exponential frequency coefficient. Consequently, kinetic factor, ka, of any chemical synthesis conducted in a RMF within its practical processing temperature range is anticipated to be significantly greater than the kinetic factor of the same synthesis conducted under conventional heating as schematically illustrated in Figure 3. According to Equation (3)—the degenerate UPKE—one may further predict: at a given reactant concentration, the rate, Rρ, of any isothermal microwave-assisted chemical synthesis is notably higher than the rate of the same synthesis under conventional field-free heating.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Characterization of reaction kinetics under field-free and RMF heating conditions using a UPKE-derived Arrhenius diagram.

Proposed rationale, analysis and conclusions on kinetics-enhancements in IMACS are fully supported by relevant process-kinetics data obtained from various types of microwave-assisted syntheses: (1) inorganic syntheses—copper oxide reduction,18, 44 carbon oxidation,45 (2) organic syntheses—fullerol formation,46 quaternary ammonium salt synthesis,47 polyamid acid synthesis,48 and (3) polymeric syntheses—carvone isomerization,49 acrylic acid crosslinking/polymerization,50 epoxy resin curing,51 and solution imidization.52

4 CONCLUDING REMARKS

This report applies the proposed unified process kinetic equation (UPKE) to demonstrate non-thermal microwave effects (NTME) on kinetics-enhancements observed in isothermal microwave-assisted chemical syntheses (IMACS). It also confirms that the use of a UPKE-derived Arrhenius diagram is adequate to fully characterize and compare macroscopic kinetics of a chemical reaction conducted under RMF heating versus the same process conducted under conventional heating.

According to mesoscopic irreversible thermodynamics, reduction in activation enthalpy of a reaction under RM irradiation is considered the major NTME, which dominantly enhances the process-rate in IMACS. This NTME is initiated from a RM energy-induced promotion of the total molar enthalpy of the irradiated reacting species at temperature. Conversely, another NTME—decrease of the pre-exponential frequency coefficient—may also occur in IMACS, which from a chemical dynamics view, is attributed to restrictions of vibrational frequency and modes of the reacting species during the reaction under RMF heating conditions.

Nevertheless, the proposed degenerate UPKE predicts that the tremendous impact of reduced activation enthalpy on the kinetics-enhancement of a highly-activated chemical process conducted under RM irradiation could normally far exceed and amply compensate the adverse kinetic setback initiated by its decreased pre-exponential frequency coefficient. As a consequence, at a given reactant concentration, global process-rate of any IMACS with a reduced activation enthalpy is expected to be significantly higher than the rate of the same synthesis conducted under conventional heating condition. Proposed rationale and conclusions on kinetics-enhancements in IMACS are fully supported by the experimental findings documented in the literature.

ACKNOWLEDGMENTS

To my family for their invaluable encouragement and support on my lifelong research efforts. Dr. Eileen A. Wong kindly reviewed and provided editorial comments on the manuscript. This study was self-motivated and self-sponsored by the author.

    CONFLICT OF INTEREST

    The author declares no financial/commercial conflicts of interest.

    AUTHOR CONTRIBUTIONS

    Boon Wong: Conceptualization (lead); data curation (lead); formal analysis (lead); funding acquisition (lead); investigation (lead); methodology (lead); project administration (lead); resources (lead); supervision (lead); validation (lead); visualization (lead); writing – original draft (lead); writing – review and editing (lead).

    APPENDIX A: Reaction-kinetics quantification—Compatibility of mesoscopic irreversible thermodynamic approach with mass-action kinetic approach

    The UPKE derived from mesoscopic irreversible thermodynamics stated in Equation (1) is
    ρ = RTЩ c α δ − 1 × { exp [ − Æ / ( RT ) ] } × { 1 − exp [ − A / ( RT ) ] } = R K × { exp [ − Æ / ( RT ) ] } × c α × { 1 − exp [ − A / ( RT ) ] } = k a × c α × { 1 − exp [ [ μ ( β ) − μ ( α ) ] / ( RT ) ] } , ()
    where A ≡ [μ(α)−μ(β)] and ka ≡ {RTЩδ−1} × {exp[−Æ/(RT)]} = {RK} × {exp[−Æ/(RT)]}: a highly temperature-dependent kinetic factor of the process, cα: concentration of the ideal reacting mixture at the initial α-state.
    According to classical thermodynamics of ideal condensed solutions/mixtures, cα may be expressed as31, 34, 37-43
    c α ≈ c αø × exp μ ( α ) − μ ø ( α ) / ( RT ) , $$ {c}_{\upalpha}\approx \left\{{c}_{\upalpha \mathrm{\o}}\right\}\times \left\{\exp \left[\left[\mu \left(\upalpha \right)-{\mu}_{\mathrm{\o}}\left(\upalpha \right)\right]/(RT)\right]\right\}, $$ ()
    where cαø, μø(α): standard concentration and standard chemical potential of the initial-state reactant, α, respectively.
    Combining Equations (A1) and (A2), one obtains:
    ρ ≈ k a × c αø × exp μ ( α ) − μ ø ( α ) / ( RT ) × { 1 − exp [ [ μ ( β ) − μ ( α ) ] / ( RT ) ] } = k a × c αø × exp − μ ø ( α ) / ( RT ) × { exp [ μ ( α ) / ( RT ) ] − exp [ μ ( β ) / ( RT ) ] } = k b × { exp [ μ ( α ) / ( RT ) ] − exp [ μ ( β ) / ( RT ) ] } , $$ {\displaystyle \begin{array}{cc}& \rho \approx \left\{{k}_{\mathrm{a}}\right\}\times \left\{{c}_{\upalpha \mathrm{\o}}\right\}\times \left\{\exp \left[\left[\mu \left(\upalpha \right)-{\mu}_{\mathrm{\o}}\left(\upalpha \right)\right]/(RT)\right]\right\}\times \left\{1-\exp \left[\left[\mu \left(\upbeta \right)-\mu \left(\upalpha \right)\right]/(RT)\right]\right\}\\ {}& \begin{array}{c}\kern0.55em \\ {}=\left\{{k}_{\mathrm{a}}\right\}\times \left\{{c}_{\upalpha \mathrm{\o}}\right\}\times \left\{\exp \left[-{\mu}_{\mathrm{\o}}\left(\upalpha \right)/(RT)\right]\right\}\times \left\{\exp \left[\mu \left(\upalpha \right)/(RT)\right]-\exp \left[\mu \left(\upbeta \right)/(RT)\right]\right\}\end{array}\\ {}& \begin{array}{c}\kern0.55em \\ {}=\left\{{k}_{\mathrm{b}}\right\}\times \left\{\exp \left[\mu \left(\upalpha \right)/(RT)\right]-\exp \left[\mu \left(\upbeta \right)/(RT)\right]\right\},\end{array}\end{array}} $$ ()
    where kb ≡ {ka} × {cαø} × {exp[−μø(α)/(RT)]}: a combined kinetic factor of the process.

    The reaction-kinetics expression, derived from mesoscopic irreversible thermodynamics, as stated in Equation (A3), is similar to Pekař's chemical kinetic expression recently reported using a mass-action kinetic approach involving rational thermodynamics of linear fluid mixtures.54, 55 In spite of their differences in perspective and rationale, both approaches result in an almost identical kinetic form and recognize the same proper driving-force expression for chemical kinetics. Compared to the traditionally-perceived driving force for chemical reactions, simply taken as the affinity, or the chemical potential difference between initial and final states,37-43 this proper driving force, governing the global chemical kinetics during the entire reaction, is identified as the difference between the exponentials of the summed chemical potentials at the initial-state α and final-state β of the process. Mathematically, it is equal to {exp[μ(α)/(RT)]−exp[μ(β)/(RT)]}, as expressed in Equation (A3).

    Biography

    • Boon Wong is a retired Materials Scientist. After earning his Ph.D. degree in Materials Science at UC Berkeley in 1975, he became Assistant Professor in Materials Engineering at Virginia Tech. Two years later, he left academia for industry. During his 37-year service in industry, he spearheaded and conducted materials and process (M&P) technology development in fields including microelectronics, photovoltaics, electrodynamics, and fracture mechanics. He has held several technical positions in industry including Technical Fellow at the Boeing Company and Chief Technologist at L-3 Communications. Since his retirement, he has been pursuing self-sponsored research in innovative M&P thermodynamics.

    DATA AVAILABILITY STATEMENT

    Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.