Seismic Fragility of Medium-Rise Soft Story SMRF Building Under Near Field, Fling Step, and Far Field Excitations

1 Introduction

Neighborhoods that are near active faults observe intense ground shaking due to near field effects. Furthermore, anomalous ground shaking can be observed in particular locations if the energy released during an earthquake propagates following forward directivity. Historical earthquakes such as the Eastern Nepal (1934), Landers (1992), Erzincan (1992), Northridge (1994), Kobe (1995), Kocaeli (1999), Duzce (1999), Chi-Chi (1999), South Iceland (2008), Gorkha (2015), among others have shown distinct features of forward directivity. For instance, during the 2015 Gorkha earthquake in Nepal, intense damage was particularly concentrated along east-west projecting stretch. The detrimental consequences of forward directivity in building structures have been recognized for quite some time now; however, quantification of seismic performance, especially in terms of seismic vulnerability, is not adequately studied so far. Bertero et al. [1] highlighted that large deformation should be attributed to the near field excitation. They recommend the incorporation of substantial ground velocity in elastic design spectra. Chopra and Chintanapakdee [2] depicted that the acceleration sensitive and displacement sensitive regions of near field records to be much wider when compared to the narrow velocity sensitive region that shifts to longer periods. They also concluded that the near field excitation demands much larger strength demand. Alavi and Krawinkler [3] demonstrated that buildings with longer periods when exposed to near field pulse like excitation reflect early yielding in upper stories. Similarly, the ductility demand is found to be gradually increased in the lower stories. Kalkan and Kunnath [4] estimated greater median maximum demands and dispersion due to the near field shaking. They highlighted that cyclic demands are more prominent in the far field strong motions which get dissipated earlier. The fling step records excite the structures in the fundamental modes, whereas the near field records with forward directivity also excite higher modes [4]. Rupakhety and Sigbjörnsson [5] outlined the contribution of higher modes in the peak inter story drift demands in tall buildings. However, they denounce the adequacy of equivalent pulses that are considered equivalent to the near field records, citing evidence of underestimation of the peak drift demand by a factor of 1.4 [5]. Sehhati et al. [6] showed that the pulse like near field forward directivity strong motions possess greater ductility demand than their far field counterparts. Sharma et al. [7] performed fragility analysis of semi-rigid steel moment frame buildings under near field and far field strong motions using incremental dynamic analysis and inferred that the peak ground velocity (PGV) to peak ground acceleration (PGA) ratio in the case of forward directivity dominantly affects the exceedance probabilities, particularly in the higher damage states. Although several studies considered near field and far field records to assess seismic performance of buildings (reinforced concrete [RC]/steel frame), seismic fragility functions are barely compared so far for soft story RC frames. The codal spectra based on stochastic process are fundamentally meant to represent the long period ground motion so they primarily represent the far field excitation [4]. Meanwhile, Alavi and Krawinkler [3] confirmed that the medium period structures can result in greater inelastic demand under high velocity pulses. Although recognized for several decades now, literature pertaining to near field effects in medium-rise RC buildings located in high seismic regions has not gotten sufficient attention so far. Several other researchers have addressed the issues of near field seismic excitation and its possible implication in various structural systems (see e.g., [8-11]).

RC construction is dominantly adopted throughout the world due to instant availability of materials and easy construction techniques. Almost all RC buildings are provided with infill walls to fulfill functionality requirements. Despite functionality demarcation, infill walls are nowadays widely recognized to provide stiffness to the structural system that checks the deformation as concluded by many researchers (see e.g., [12-22]). It is common to observe medium to high rise RC buildings with open ground stories either for shop outlets or parking purposes. Thus, due to the lack of infill masonry in one story leads to the development of soft story mechanism. The Indian Standard (IS) 1893 (Part1): 2016 defines soft story as the one with lateral stiffness less than 70% of the story above or less than 80% of the average lateral stiffness of the three stories above [23]. Soft story damage was observed in many medium to high rise RC buildings during the 2015 Gorkha earthquake [24] due to lack of adequate stiffness as largest seismic demand is expected in the same story.

Medium to high rise RC buildings are mainly constructed for residential and commercial purpose in Nepal [25]. To accommodate the growing parking demand as well as providing a wider shop outlet display, most of such buildings are constructed as soft story constructions. The same case is also widely observed in many parts of the world. In the highly active seismic regions such as the Himalayas, both near field and far field earthquakes are expected to excite these buildings. Thus, to quantify seismic vulnerability of soft story medium-rise RC frame buildings, seismic vulnerability under near field, fling step, far field, and mixed strong ground motions is quantified in terms of fragility functions.

2 Materials and Methods

2.1 Prototype Building

A seven story RC frame building adhering to a typical medium-rise construction in Nepal is considered for seismic vulnerability analysis. Both Nepal Building Code (NBC) and Indian Standard (IS) Code of Practice are used to design such buildings. All medium-rise SMRF buildings constructed after legal enforcement of NBC in Nepal in 2003 are engineered constructions. Notably, by-laws were in use to design similar buildings before legal enforcement [24, 26]. Generally, site investigation is done before designing such buildings. The geometrical details of the case study structure and loading considerations are summarized in Table 1. The exterior walls are provided with 230 mm thick double wythe brick masonry infills in cement mortar (1:4). A typical plan of the case study building is shown in Figure 1. Similarly, sectional details of beams and columns are presented in Figures 2 and 3, respectively.

Table 1. Geometrical features, loading consideration, and structural details of the case study building.

Component	Description	Details
Frame	Type	Special moment resisting frame (SMRF)
	No. of stories	7
	No. of bays in X-direction	4
	No. of bays in Y-direction	5
	Story height	3.2 m
	Total width along X-axis	20.55 m
	Total width along Y-axis	25.59 m
	Size of beam	350 × 550 mm
	Size of column	500 × 500 mm
	Thickness of slab	125 mm solid RC slab
	Isolated square footing	3.4 × 3.4 m, 3.1 m below the plinth level
Load	Live load at floor slab	2 kN/m2
	Live load at roof	1.5 kN/m2
	Staircase load	3 kN/m2
	External wall load	For 230 mm thick brick masonry wall: 13.5 kN/m (no opening) and 10.8 kN/m (with openings)
	Internal wall load	10.8 kN/m
Material	Grade of concrete	M-25 (28 days cube compressive strength of 25 MPa)
	Grade of reinforcement	Fe-500 (yield strength: 500 MPa)
	Brickwork	10 MPa bricks in 1:4 cement sand mortar for 230 mm thick solid brick walls

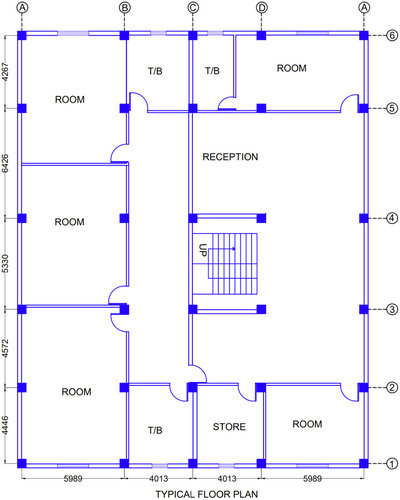
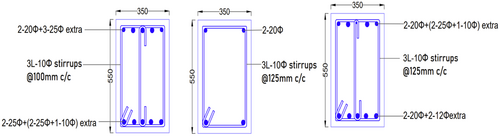
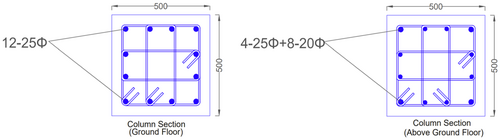
2.2 Infill Wall Modeling

The properties of masonry infill walls vary per the type of masonry units and mortar joints. Two numerical modeling techniques are widely adopted to model infill walls in RC buildings: micro models (plane finite element) and macro model (equivalent strut model). The first one is based on continuum theory, which provides accurate results of both material and geometrical aspects of infill panels. However, micro modeling is usually executed in component modeling since it is computationally expensive [27]. On the other hand, macro models use equivalent diagonal struts. Equivalent struts are relatively easy to model, especially when mechanical properties are not readily available. Due to the lack of experimentally identified mechanical properties, we also adopted macro modeling approach in this study. First class solid bricks with 10.8 kN/m³ unit weight, 10 MPa compressive strength, and H2 mortar type are considered to estimate properties of the equivalent struts (Figure 4). The width of the equivalent strut (W_ds) per the IS 1893–2016 [23] can be estimated as:

$$W_{\mathit{ds}}=0.175{\alpha }_h^{-0.4}{L}_{\mathit{ds}}$$()

$${\alpha }_h=h\times \left(4\sqrt{\frac{E_{m}t\sin 2\theta }{4E_t{I}_{c}h}}\right)$$()

where E_m is the modulus of elasticity of the infill material, E_t is the elastic modulus of the RC frame, I_c is the moment of inertia of the adjoining column, t is the thickness of the infill wall, $h$ is the height of the wall, and θ is the angle of the diagonal strut with the horizontal. The length of the equivalent diagonal strut (L_ds) is calculated as:

$$L_{\mathit{ds}}=\sqrt{{\left(L_w\right)}^2+{\left(h_c\right)}^2}$$()

where, $L_w$ is the length of infill wall and $h_c$ is the clear height of column. Per Paulay and Priestly [28], the width of the unreinforced masonry infill wall with openings can be estimated as:

$$W_{\mathit{do}}={\rho }_w{W}_{\mathit{ds}}$$()

where, ${\rho }_w=1-2.5A_r$, where $A_r$ is the opening percentage in the wall.

The modulus of the elasticity of the infill masonry is considered as:

$$E_m=550f_m$$()

where, the compressive strength of masonry prism ($f_m$) is given as follows:

$$f_m=0.433f_b^{0.64}{f}_{m0}^{0.36}$$()

where, f_b is the compressive strength of brick and f_mo is the compressive strength of mortar.

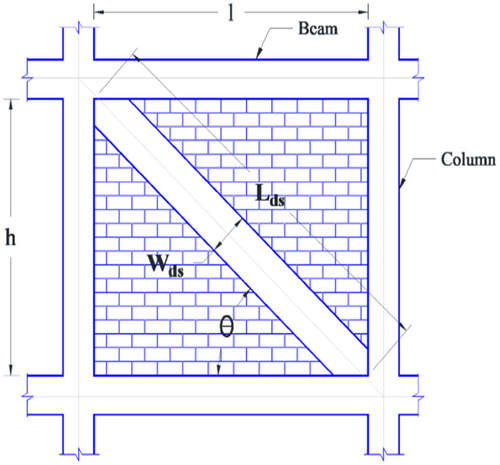
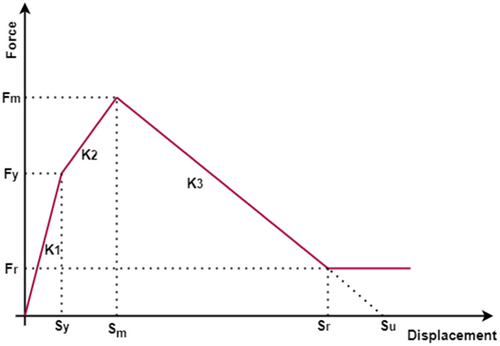
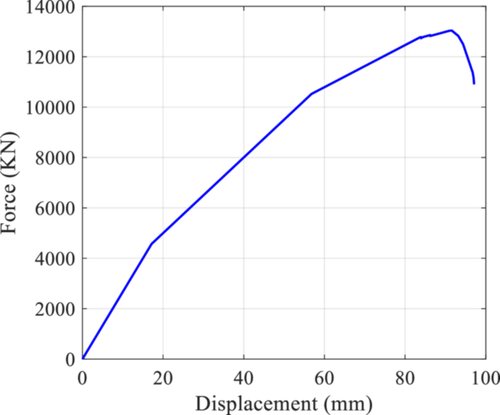
Equivalent diagonal struts are assigned using link elements for 230 mm thick walls, whereas 115 mm thick partition walls are considered for dead load contributions only. Nonlinear behavior of masonry infill wall is modeled using the properties estimated from the empirical formulations proposed by Panagiotakos and Fardis [29]. An example of multilinear force-displacement plot for masonry infill wall is shown in Figure 5. The four segments of the multilinear curve respectively represent the uncracked panel, separation of diagonal strut from the panel, softening of infill wall once the critical displacement (S_m) is achieved, and zero residual strength segment (S_u). There are several approaches to incorporate infill walls in numerical modeling including the equivalent viscous damping approach [30, 31]. The choice of modeling approach is mainly based on the availability of variable values. Considering the availability of variable values, we selected the approach proposed by Panagiotakos and Fardis [29].

2.3 Numerical Modeling

Beams and columns are modeled using one-dimensional line elements. Slab sections are modeled using thin shell elements, considering only in-plane stiffness by assigning rigid floor diaphragm. 230 mm thick infill masonry walls are modeled using multilinear plastic compression only link elements. To replicate the soft story mechanism, the ground story is modeled as a bare frame system. The numerical model is created in ETABS v18.1.1 [32]. The three-dimensional numerical model is shown in Figure 6. Nonlinear hinges are assigned to incorporate nonlinearity in the frame elements at 10% of their respective lengths as per the FEMA-306 provisions [33]. Static nonlinear analysis (pushover analysis) is carried out to assess the capacity of the structure. Similarly, nonlinear time history analysis is carried out using the direct integration method to predict displacement demands under three types of strong motions as detailed in the next section.

2.4 Strong Motion Records

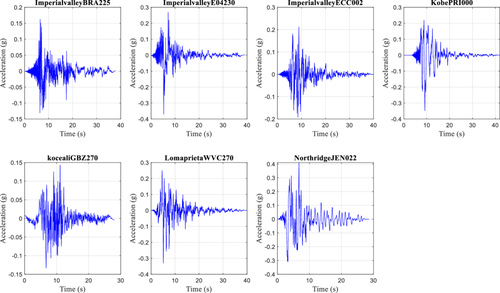
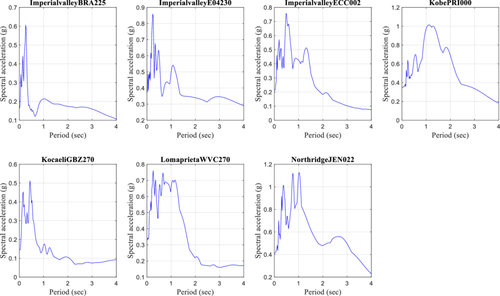
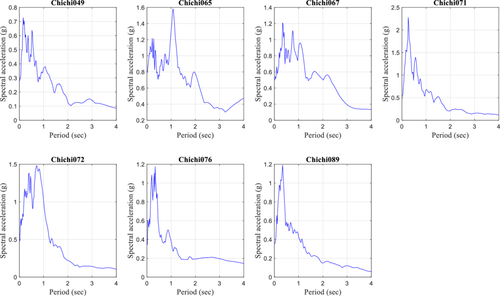
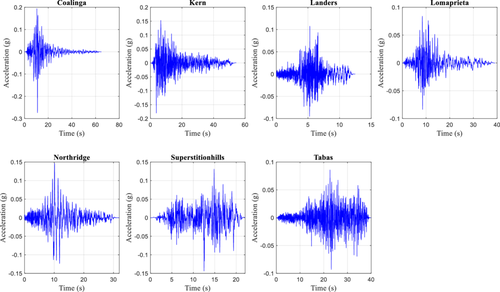
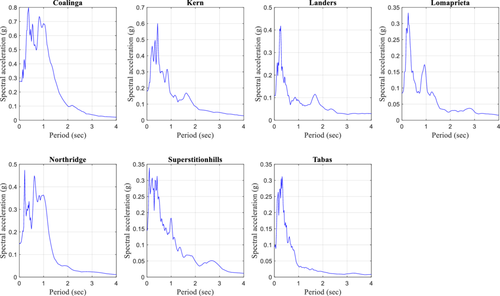
To quantify seismic response of the building, three types of strong motion records were selected. The first is near field record, which is select based on the Joyner-Boore distance (R_jb) less than 10 km as shown in Table 2. The near field records are also plotted in Figure 7 and the respective 5% damped response spectra are shown in Figure 8. Forward directivity occurs due to the rupture propagation direction toward the site with relatively similar shear wave velocity and rupture velocity. Forward directivity is characterized by long period pulse in the initial shaking phase due to the occurrence of elastic energy intensely in a congregated form [34]. The rupture mechanism can lead to the residual deformation that occurs from tectonic displacement and gives rise to a unidirectional large amplitude velocity pulse together with the displacement time history comprising monotonic step [4]. The fling step strong motions as used by Kalkan and Kunnath [4] also used in this study. Details of fling step strong motion records are presented in Table 3. The fling step accelerograms used in this study are also shown in Figure 9 and the respective 5% damped response spectra are plotted in Figure 10. Notable impacts of fling step shaking were recognized during the 1994 Northridge earthquake [34]. Permanent displacement during the near field earthquake is caused by permanent fault translation undergirded by step displacement and unidirectional velocity pulse. In fling step strong motions, displacement and directivity effects are coupled in the same direction [34]. Far field shaking is contributed by the surface waves and characterized by the long period motion. Far field excitations are known to affect mostly the long period structures. Far field excitation must pass through both path and site effects thus yields destructive consequences in particular structural forms even in distant locations. For far field effects, strong motion records having R_jb > 15 km were considered. The details of the select far field records are shown in Table 4. Time history records used for far field excitation are shown in Figure 11 and the respective 5% damped response spectra are plotted in Figure 12. Since it is voluminous to present all the strong motion records used in analytical modeling, we have provided the file name in the first column of each table so that interested readers may seamlessly download from the PEER database. Separate interpretations regarding each type of strong motion can be found in standard literature elsewhere.

Table 2. Near field strong motion records [35].

Strong motion component	Moment magnitude (MW)	Rjb (km)	PGA (g)	PGV (cm/s)	PGV/PGA
Kobe (1995) PRI000	6.90	3.31	0.33	82.18	249.03
Koceali (1999) GBZ270	7.51	7.57	0.14	27.46	196.14
Imperial Valley (1979) BRA225	6.53	8.54	0.16	36.60	228.75
Imperial Valley (1979) ECC002	6.53	7.31	0.23	41.97	182.47
Imperial Valley (1979) E04230	6.53	4.90	0.39	76.99	197.41
Loma Prieta (1989) WVC270	6.93	8.48	0.39	60.50	155.12
Northridge (1994) JEN022	6.69	0.0	0.43	83.72	194.69

Table 3. Fling step strong motion records [35].

Strong motion component	Moment magnitude (MW)	Rjb (km)	PGA (g)	PGV (cm/s)	PGV/PGA
Chi-Chi (1999) TCU049-E	7.62	3.76	0.28	38.98	139.21
Chi-Chi (1999) TCU065-E	7.62	0.57	0.83	140.59	169.38
Chi-Chi (1999) TCU067-E	7.62	0.62	0.51	102.42	200.82
Chi-Chi (1999) TCU071-E	7.62	0.0	0.53	45.30	85.47
Chi-Chi (1999) TCU072-E	7.62	0.0	0.50	61.21	122.42
Chi-Chi (1999) TCU076-E	7.62	2.74	0.29	62.28	214.75
Chi-Chi (1999) TCU089-E	7.62	0.0	0.33	30.58	92.66

Table 4. Far field strong motion records [35].

Strong motion component	Moment magnitude (MW)	Rjb (km)	PGA	PGV	PGV/PGA
Northridge (1994) LV5000	6.69	37.47	0.15	14.98	99.86
Tabas (1978) FER-L1	7.35	91.14	0.09	5.14	57.11
Kern (1952) TAF111	7.36	38.42	0.18	16.89	93.83
Coalinga (1983) H_H-Z14090	6.36	28.11	0.27	30.90	114.44
Superstition Hills-02 (1987) B_B-BRA225	6.54	17.03	0.15	10.70	71.33
Loma Prieta (1995) SUF090	6.93	47.41	0.08	7.74	96.75
Landers (1992) BAK050	7.28	87.94	0.12	9.88	82.33

3 Results and Discussions

The modal analysis resulted in the first two modal frequencies of 1.31 and 1.53 Hz, respectively along X- and Y-directions (see Figure 6). The corresponding mass participation ratios are 0.872, and 0.893. The pushover curve for the prototype building is shown in Figure 13. The yield displacement and ultimate displacement are defined based on the approach proposed by Elnashai and di Sarno [40] through graphical interpretations. Once capacity limits for each damage state are defined, fragility functions are derived using displacement demands obtained from nonlinear time history analysis.

Fragility functions for medium-rise soft story RC frame building for near field, fling step, far field, and mixed strong ground motion scenarios are constructed using the capacity and demand values. Three IMs: PGA, PGV, and spectral acceleration (S_a) are considered to develop fragility functions. Figure 14 shows fragility functions considering PGA as IM. The NBC 2020 recommends 0.4 g as the maximum considered earthquake (MCE) PGA for many locations across the country. Thus, the maximum PGA line is also drawn together with the fragility functions for comparison and interpretation. Figure 14a shows fragility functions for medium-rise soft story SMRF building under near field excitation. The exceedance probabilities of slight, moderate, extensive, and collapse damage states are respectively ~85%, 40%, ~25%, and ~10% at 0.2 g, which can be considered as the design basis earthquake (DBE) PGA. The exceedance probabilities of slight, moderate, extensive, and collapse damage states at 0.4 g are respectively ~98%, ~85%, ~75%, and ~55%. This indicates that when PGA equivalent to the MCE PGA occurs, significant number of soft story SMRF buildings are expected to collapse, otherwise a large portion of such buildings will be unoccupiable as demonstrated by the exceedance probability of the extensive damage state. It should be noted that almost all medium-rise soft story buildings will observe considerable damage at MCE PGA.

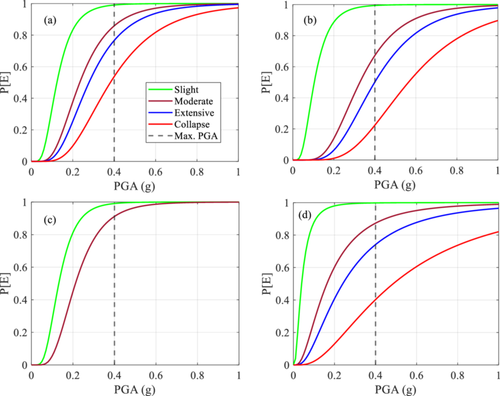
Figure 14b shows fragility functions for medium-rise soft story buildings under fling step excitation. At 0.2 g, exceedance probabilities of slight, moderate, extensive, and collapse damage states are estimated as ~90%, ~15%, ~10%, and ~2%, respectively. The exceedance probabilities outline that the fling step excitation causes slight damage almost equally as that by near field excitation. However, for the other damage states, near field shaking gives rise to higher exceedance probabilities than the fling step. At 0.4 g, the exceedance probabilities for slight, moderate, extensive, and collapse damage states are respectively ~99%, ~65%, ~50%, and ~20% under fling step excitation. It is evident that even at the MCE PGA, near field excitation will reflect more damage probabilities for moderate, extensive, and collapse damage states than that by the fling step excitation. The probability of collapse of medium-rise soft story SMRF buildings is almost 2.5 times higher due to the near field excitation when compared to the fling step excitation at 0.4 g.

Figure 14c shows the fragility functions for medium-rise soft story SMRF buildings under far field excitation. As confirmed by the demand to capacity ratio, far field excitations triggered only slight and moderate damage states. Thus, fragility functions are developed for only two damage states. It is worth noting that the 2015 Gorkha earthquake PGA was around 0.2 g in Kathmandu Valley. Many medium-rise soft story buildings used for residential, commercial, or residential cum commercial (ground story as commercial space) observed minor to moderate damage due to the Gorkha earthquake; basically, reflecting damage to infills and other nonstructural components. Although some medium-rise buildings collapsed during the Gorkha earthquake or sustained extensive damage state in the Kathmandu Valley [24], such buildings were not fundamentally the SMRF constructions. Almost all collapsed or extensively damaged medium-rise buildings in Kathmandu Valley during the Gorkha earthquake were buildings with added stories and substandard construction systems without proper design and detailing.

Figure 14d shows the fragility functions for medium-rise soft story SMRF buildings when mixed ground motion records are used. All three batches of the ground motions were used to derive fragility functions for medium-rise soft story SMRF building. As shown in Figure 14d, lower damage states are more constrained by far field records, whereas higher damage states (extensive and collapse) are more aligned toward near field and fling step excitations. Since both near field and fling step excitations occur near the fault rupture, near field and fling step excitations govern the higher damage states accordingly. It should be noted that the collapse damage state is underestimated if ground motions are mixed to construct fragility functions. For example, the exceedance probability of collapse damage state under near field excitation is ~55%, whereas that under mixed ground motion excitation is ~40% only at 0.4 g. It should be noted that medium-rise soft story SMRF buildings situated in near field regions may show a deviation in collapse statistics if fragility functions developed using mixed ground motions are used in pre-earthquake seismic risk studies. If only fling step ground motions are used to develop fragility functions for medium-rise soft story SMRF buildings, they will reflect conservative estimates for moderate, extensive, and collapse damage states when compared with mixed ground motions. For example, the exceedance probabilities of moderate, extensive, and collapse damage states are respectively ~65%, ~50%, and ~20% at 0.4 g under fling step excitation. On the other hand, the mixed ground motion fragility functions indicate ~85%, ~75%, and ~40% respectively for moderate, extensive, and collapse damage states at 0.4 g. This indicates that moderate and extensive damage states are dominated by near field strong motion than any other type of shaking. Meanwhile, slight damage state is more precisely characterized by the fling step excitation when fragility functions based on mixed ground motions are constructed. Although mixed ground motion excitation nearly averages the exceedance probabilities between the near field and fling step excitations for collapse damage states, the use of collapse fragility function derived from fling step excitation should be cautiously interpreted since the occurrence of near field shaking without fling step may readily alter the damage scenario.

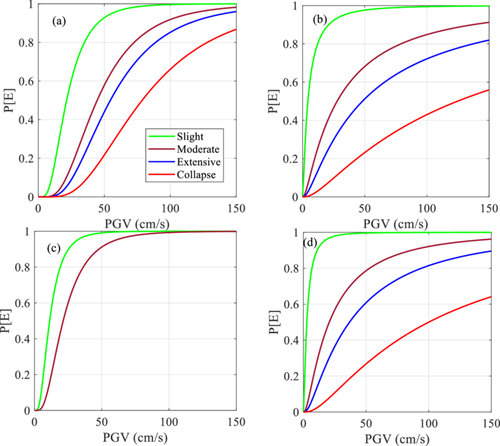
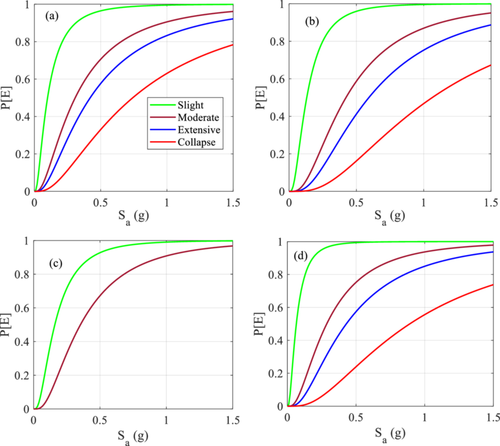
Figure 15 shows the fragility functions for medium-rise soft story SMRF buildings considering PGV as IM under near field, fling step, far field, and mixed strong motion excitations. Similarly, Figure 16 shows the fragility functions for medium-rise soft story SMRF building considering spectral acceleration (S_a) as IM under near field, fling step, far field, and mixed strong motion excitations. Both Figures 15 and 16 closely resemble Figure 14. This indicates that the fragility function is seldom affected by the choice of IMs between PGA, PGV, and Sa. The trend in terms of greater or lesser exceedance probabilities under various types of excitations is identical in all three IMs. The two sets of fragility functions presented in Figures 15 and 16 could serve as reference fragility functions in the future. For example, the velocity records from seismometers can be used to compare or calibrate the analytical fragility functions using the future earthquake damage data. Also, spectral acceleration at fundamental vibration period is widely used in structural engineering. In this case, Figure 16 can be used as a reference fragility function under various excitation schemes. Since there is no direct conversion scheme between PGA, PGV, and S_a, respective fragility functions can be used based on intended IM value.

4 Conclusions

Medium-rise soft story SMRF buildings are dominantly constructed in high seismic regions for residential and commercial purposes. Due to the lack of infill walls on ground story, the stiffness deficit transforms such structures into soft story constructions. Considering the lesser attention toward seismic vulnerability of medium-rise SMRF buildings, fragility functions for near field, fling step, far field, and mixed earthquake excitations are developed. Starting from the performance scenario of similar building class during the 2015 Gorkha earthquake in Nepal, three sets of fragility functions considering PGA, PGV, and Sa are derived. The results highlight that the conventional mixed strong motion fragility functions will not be representative enough for the near field excitations. Similarly, fling step fragility functions are found to be conservative in representing the higher damage states when compared to the near field scenario. In addition, the far field excitation was found to be incapable of triggering higher damage states (extensive and collapse) in medium-rise soft story SMRF buildings, although the occurrence of lower damage states is relatively high. Such nonoccurrence is supported by the demand to capacity ratio less than 1 in any of the strong motion records deployed in time history analyses. Since ductility of the case study building that typically represents medium-rise SMRF construction is greatly contributed by thorough ductile detailing and well-sized structural members, nonoccurrence of the higher damage states under far field excitation is rationally justified. In the case of the occurrence of the PGA equivalent to the MCE PGA (0.4 g), a vast majority of medium-rise soft story SMRF buildings will not be usable due to the occurrence of higher damage states (extensive and collapse) under near field and fling step ground excitations. If one has to assess seismic vulnerability of medium-rise soft story SMRF buildings in near field regions, only near field records are recommended to be used rather than mixed strong ground motions. Improvements are deemed achievable by conditioning and updating fragility functions when experimental or empirical data are available.

Conflicts of Interest

The authors declare no conflicts of interest.