The Impact of Flow Velocity on Environmental DNA Detectability for the Application in River Systems
Funding: This study was part of the project ‘DECODE-bioDivErsity estimate for aquatiC ecOsystems aDopting eDNA’ (TU09) which was funded by the ‘Topconsortium voor Kennis en Innovatie’ (TKI). The authors additionally acknowledge support from TU Delft internal funds through the Delta Transport Processes Laboratory.
ABSTRACT
Organisms perpetually release genetic material in their surroundings, referred to as environmental DNA (eDNA), which can be captured and subsequently analyzed to detect biodiversity across the tree of life. In lotic, dynamic environments, little is known about the specific factors that affect the concentration of eDNA between release by the host and its dissemination into the environment. This gap in knowledge introduces significant uncertainty when applying eDNA as a monitoring tool. Our objective is to provide insight on the factors that affect the eDNA concentrations in ecosystems representative of rivers and streams. To this end, we conducted a series of laboratory experiments in a rotating circular (annular) flume, which allows for extended degradation experiments under conditions of flow. Here, we show that flow velocity impacts the observed eDNA concentration over time. Our results suggest that flow-induced transport keeps eDNA in suspension, reducing eDNA removal from the water column, which increased the observed concentration of eDNA. We observed a temporary increase in eDNA concentration over the early phase of the flume experiment with the highest flow velocity. This increase in eDNA concentration seems to be due to a combination of low eDNA degradation rates and high shear stress, which fragment and subsequently homogenize eDNA particles over the water column. The results of our study show the importance of better understanding and assessing the detection probability of eDNA, both in controlled laboratory and larger-scale environmental conditions.
1 Introduction
Over the past decades, freshwater ecosystems have been exposed to numerous human-induced stressors, such as pollution, land use change, and overexploitation (Dudgeon et al. 2006). As a result of these stressors, freshwater biodiversity has disproportionately faced population declines and risks of species extinction compared to its marine and terrestrial counterparts (Strayer and Dudgeon 2010; Reid et al. 2019; WWF 2022). River restoration is an established method to combat the current decline of freshwater biodiversity and to ultimately rehabilitate river ecosystems (WWF 2022; Wohl et al. 2005). Restoration campaigns require the collection of monitoring data to evaluate the efficacy of varying restoration practices. So far, a minority of restoration projects has been evaluated through monitoring (England et al. 2021).
The capture of genetic material from a subject species' environment, followed by genetic testing, is a means to monitor a species' presence. Organisms perpetually produce and release genetic material in their environment, which is known as environmental DNA, or eDNA. This material is either free-floating or encapsulated in the form of cells, tissues, gametes, or organelles (Pawlowski et al. 2020). The analysis of eDNA as a biomonitoring tool has gained enormous traction over the last decades, as it may allow for rapid standardized biomonitoring across the tree of life (Avó et al. 2017; Ruppert et al. 2019). eDNA-based biomonitoring can provide a solution to the restoration-related challenges raised above, as it is less dependent on taxonomic expertise for species identification and is cheaper than traditional monitoring methods (Lugg et al. 2018). However, a remaining obstacle for the adoption of eDNA-based monitoring in cases of river restoration is the lack of knowledge on processes that impact eDNA decay rates between the moment of release by its source organism and its dissemination into the environment. For the monitoring of rivers and streams (i.e., lotic ecosystems), understanding how eDNA moves after release (i.e., the transport of eDNA) and how eDNA degrades (i.e., the fate of eDNA) is especially relevant (Barnes and Turner 2016).
After release, the transport of eDNA results in a spatial discrepancy between the genetic signal and its point of release. The extent of this discrepancy is determined by both the rate of eDNA transport and the rate of eDNA degradation. Previous studies on the transport of eDNA in river systems have shown that, depending on the monitored system, the maximum travel distance ranges from meters (Pilliod et al. 2014) to kilometers (Deiner and Altermatt 2014; Pont et al. 2018; van Driessche et al. 2023). River discharge has a significant positive relation with eDNA transport distance (Jane et al. 2015; Wilcox et al. 2016) and therefore is a key consideration when approximating transport distance (Carraro et al. 2018). Both the transport and degradation of eDNA depend on the interaction between the state of the eDNA particle and the environmental conditions. For example, Jane et al. (2015) argued that partial, whole, and clumped cells might settle more quickly under low flow velocities, whereas these particles may remain in suspension due to turbulent mixing at high flow velocities, resulting in an increased eDNA transport distance. As another example, mineral particles efficiently adsorb extracellular eDNA, effectively changing the state of these eDNA particles (Sand et al. 2024). The adsorption efficiency of nucleic acids is influenced by the mineral surface charge, the mineral surface composition, and the pH, salinity, and composition of the surrounding solution (Feuillie et al. 2015). Upon adsorption, the lifespan of the extracellular eDNA is significantly increased, and its advection-driven mode of transport likely changes to align with the mineral's transport pathways. Likewise, the fate or degradation of eDNA is driven by multiple environmental conditions. For instance, moderately high temperatures (Strickler et al. 2015; Jo et al. 2019, 2020), as well as low pH, accelerate degradation (Strickler et al. 2015; Kagzi et al. 2022; Zhao et al. 2023), and contradictory evidence has been found on the impact of ultraviolet B radiation (UV-B) on degradation rates (Strickler et al. 2015; Mächler et al. 2018). With regard to dynamic environments, Shogren et al. (2018) tested whether flow velocity impacts eDNA persistence in artificial recirculating streams. With flow velocity impacting the degradation rate for only a few of the tested markers, the authors concluded flow to have little effect. In contrast, research for wastewater treatment purposes shows that shear stress in turbulent flows affects the particle shape and size of human feces (Davies et al. 1997; Penn et al. 2019), as well as activated sludge flocs, i.e., aggregates of microbes and suspended solids (Li and Leung 2005; Yuan and Farnood 2010). Given these results, we hypothesize that the observable concentrations of environmental DNA, a component of both fecal material and activated sludge, are affected by flow. So far, eDNA degradation experiments have mostly been performed in ponds and static controlled (mesocosm or laboratory) setups (e.g., Kagzi et al. 2022; Wood et al. 2020). At this time, the impact of flow on environmental DNA concentrations remains an understudied topic, which needs to be investigated further for its application in lotic systems.
This study focuses on the temporal change of eDNA concentrations under the dynamic conditions of flow present in rivers and streams. To this end, a set of laboratory experiments was conducted employing a rotating circular (i.e., annular) flume, simulating the simplified condition of constant flow velocity.
2 Materials and Methods
2.1 Experimental Setup
The rotating annular flume allowed for the performance of multi-day eDNA degradation experiments at a constant flow velocity, without introducing, e.g., paddles, wheels, or pumps that might influence the observed eDNA concentrations while the water is recirculated. The annular flume featured counter-rotating top lid and bottom components in order to minimize the formation of secondary flow cells which commonly occurs in curved systems. The flume diameter to the middle of the channel was equal to 3.7 m, channel width 0.3 m, channel and flow depth equal to 0.2 m, and water volume equal to 700 L. A tangential velocity ratio () was adopted following past hydraulic investigations in this setup to minimize the formation of the secondary flow (Booij 1994). We performed eDNA degradation experiments under four flow rates, each lasting for 7 days (Figure 1). Although sediment is typically present in natural lotic systems, this was not included in the experiment. By doing so, the complexity of data acquisition and its subsequent interpretation was reduced. Prior to each experiment, the flume was cleaned with commercial 5% bleach and rotated at a low velocity ( m s−1) for 30 min. The flume was subsequently rinsed to remove traces of bleach and refilled with potable tap water 60 min before the initiation of each experimental run. During the daytime, the experimental setup was primarily illuminated by artificial lighting, which was on daily from around 06:45 to 23:00, while sunlight provided a minor indirect and scattered source of light. At night, an LED spotlight was used to illuminate the flume for safety reasons.
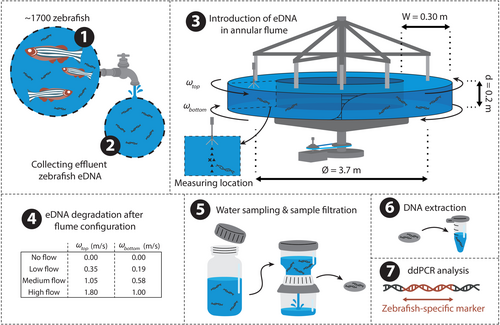
The source of eDNA was wildtype zebrafish (Danio rerio) rearing water, collected at the zebrafish facility of Leiden University. The source population consisted of roughly 1750 individuals, which spent the majority of their lives in a total volume of 500 L of water (spread across 50 tanks of 10 L each). All tanks drained through a single pipe, where approximately 60 L of mixed outflowing rearing water was collected 60 min before initiation of each experiment and added to the flume 15 min before initiation of each experiment. The flume was rotated at low velocity ( m s−1) for 15 min to homogenize the eDNA throughout the flume, after which each experiment was initiated. Four experiments were conducted, each with a constant flow velocity for seven consecutive days. The respective rotation velocities of the top lid of the four experiments were 0.00, 0.35, 1.05, and 1.80 m s−1, which will hereafter be referred to as ‘no flow’, ‘low flow’, ‘medium flow’, and ‘high flow’ respectively. Daily sample and evaporation volume were estimated to be 1%–2% of total volume and were replaced with potable tap water.
2.2 Particle Analysis
In order to characterize the size of the introduced eDNA particles, a particle size distribution (PSD) analysis was performed on two water samples of 1 L retrieved from the zebrafish culturing facility at Leiden University using a Malvern Master Sizer 2000 (Malvern Panalytical, Almelo, the Netherlands). The water samples were placed in a glass beaker. Samples were suspended in the beaker using a paddle and pumped through the Malvern Master Sizer back into the mixing beaker using a peristaltic pump. To further examine the structure of the eDNA source material, solid particles were collected from the bottom of the zebrafish culturing containers. Particles were subsequently examined (Figure 2) under a VHX-5000-series digital microscope (KEYENCE, Mechelen, Belgium), and maximum particle diameter and particle surface area were recorded (see Figure S1). These microscopy particle measurements were used to inform the particle bonding strength model as described in Section 2.4.

2.3 Experimental Conditions
Temperature (G 1720 thermometer; Greisinger, Regenstauf, Germany), pH (G 1501 pH meter; Greisinger, Regenstauf, Germany), and electrical conductivity (GMH 3431 conductivity meter; Greisinger, Regenstauf, Germany) were measured to characterize the experimental conditions. These measurements were conducted in triplicate and at equally spaced locations across the annular flume after the collection of the water samples at each time point. Temperature (15.3°C ± 1.1°C), pH (8.1 ± 0.3), and electrical conductivity (527 ± 7 μS cm−1) were consistent between experimental runs and are comparable to measured values in river systems globally (Virro et al. 2021).
The shear stresses to which the eDNA was subjected were approximated by measuring vertical profiles of horizontal flow velocity using an acoustic doppler velocimeter (ADV; Nortek Vectrino). The ADV was positioned laterally in the middle of the flume, 15 cm from either side wall. We suspended 185 mL of glass seeding (Ø = 30 μm; ρ = 1001 kg m−3) to introduce a retrievable signal for the ADV. Settings were the following: sampling rate equal to 100 Hz, transmit length was 1.8 mm, sampling volume equal to 2.5 mm, and the speed of sound was set to 1480 m s−1. Velocity measurements with corresponding signal-to-noise ratios below 5 dB or above 25 dB, or with normalized correlation values below 70% were discarded. The ADV could not measure the upper 6 cm of the water column due to its focal point being located 5 cm away from the transducers, as well as mounting constraints. The velocity measurements were compared with measurements from a previous annular flume investigation under near-identical conditions (Booij 1994).
2.4 Hydrodynamic Analysis

2.5 Water Sampling and DNA Extraction
We collected eDNA through water sampling from the annular flume using 50 mL BD Plastipak sterile syringes (VWR International, Radnor, PA, USA) at six longitudinally evenly spaced locations in the annular flume. The six subsamples were combined, of which 300 mL was filtered through a Whatman glass microfiber filter (Ø = 47 mm, pore size of 1.2 μm) in a sterile Nalgene filter column, using a vacuum pump. Samples were collected in triplicate at 0, 3, 6, 12, 24, 36, 48, 72, 144, and 168 h after initiation, for a total of 30 samples per experimental run, with the 0-h measurement representing the initial concentration after introduction into the flume. Filters were halved (one half for extraction, and one half was kept as a backup) and individually stored in 2 mL DNase/RNase-free Eppendorf tubes at −80°C until extraction. DNA was extracted from each sample using the DNA/RNA Mini Prep Plus Kit (Zymo Research, Irvine, CA) including the optional DNase I treatment, while making use of QIAshredders (Qiagen, Venlo, the Netherlands), as described in Marshall et al. (2021). The following minor modifications were implemented: samples were gently shaken at 350 rpm during initial incubation (55°C for 60 min), 700 μL of each sample-lysis buffer mixture (out of a total volume of 1900 μL) was added to the Spin-Away Filters (Zymo Research, Irvine, CA), and final elution was done in 55 μL DNase/RNase-free water at 16,000×g for 1 min. A negative extraction control was processed along with each set of extractions to test for contamination. We stored the purified DNA at −80°C awaiting amplification.
2.6 ddPCR Analyses
| Sequence name | Sequence (5′–3′) | Length (bp) | Amplicon length (bp) | ddPCR annealing temperature (°C) |
|---|---|---|---|---|
| ZebCO1-17F | F: GGTGCTTGAGCCGGAATAGT | 20 | 73 | 55 |
| ZebCO1-89R | R: GTGCTCCTGGTTGGCTAAGT | 20 | ||
| ZebCO1_41P | FAM-ACCGCATTAAGCCTCTTAATCCGA-BHQ1 | 24 |
2.7 Statistical Analyses
3 Results
Digital microscope images suggested that particles contained varying degrees of leftover fecal matter, food pellets, and microorganisms. Particles were heterogeneous in size (ranging from microns to hundreds of microns), shape, and composition (Figure 2). Visual inspection of these suspended particles further revealed the presence of intact Ciliophora. These microorganisms were omitted from the microscopic measurements of particle diameter and surface area. Their presence implies that the introduced zebrafish water did not contain strictly zebrafish-related eDNA particles, which potentially biases the indiscriminate PSD output. The bulk of the particles measured on the Malvern Master Sizer 2000 were of the order of 100–1000 μm (Figure 3C). The calculated bonding strength of these eDNA aggregates ranged between 4.8 × 10−3 and 8.6 × 10−2 Pa, assuming that the primary particles in a given eDNA aggregate were closely spaced (0.01 μm apart).
Implemented negative extraction and amplification control samples produced an average of 0 (±0) and 0 (±1) positive droplets in the ddPCR analyses, with a total of 14,725 (±2112) and 16,637 (±1601) accepted droplets respectively. eDNA was detected in all samples regardless of the time of sampling and yielded an average of 35 (±23) positive droplets in an average of 14,403 (±1849) total droplets. Under conditions without flow (Figure 4A), at the start of the experiment (t = 0 h in Figure 4A), eDNA concentration ranged between 6 and 9 copies mL−1, then reduced to 2–7 copies mL−1 at the 72 h mark and then remained constant at 3–5 copies mL−1, with a decay rate constant of 0.0033 h−1. For low flow conditions (Figure 4B), concentrations remained constant at 2–10 copies mL−1 throughout the run ( = −0.000086 h−1). According to the post hoc Tukey's test, the estimated degradation rate for the low flow treatment was statistically indistinguishable from zero, as the 95% confidence interval ranged between −0.002 and 0.003. For the medium flow conditions (Figure 4C), eDNA concentrations ranged between 3 and 10 copies mL−1 and remained constant for the full duration of the experiment ( = 0.0023 h−1), although it was distinguishable from zero according to Tukey's test. In the case of the high flow conditions (Figure 4D), eDNA concentrations ranged between 10 and 20 copies mL−1 at the start of the experiment and proceeded to increase to 20–50 copies mL−1 at the 48 h mark. Afterwards, eDNA concentrations decreased to 4–5 copies mL−1 at the end of the experiment ( = 0.0049 h−1). Overall, the slope of the eDNA time series curves increased (became less negative) in the low and medium flow runs compared to the no flow run.
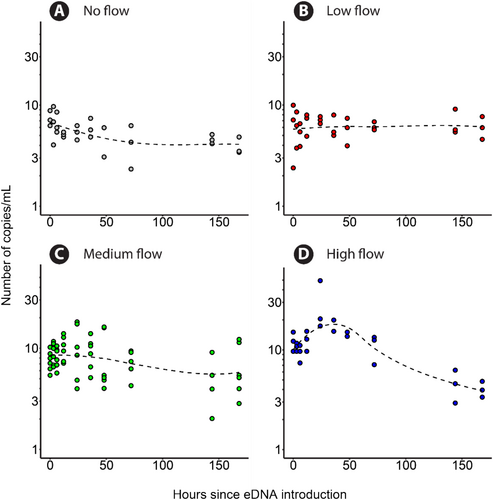
The linear regression model explained 42% of the variance in eDNA concentration (R2 = 0.44; adjusted R2 = 0.42). The model results showed a significant negative effect of time in the case of the low flow treatment (p = 0.019) on eDNA concentration. The initial eDNA concentrations were significantly different for both the medium flow (p = 0.0014) and high flow (p < 0.001) treatments when compared to the no flow treatment. The high flow treatment exhibited a significant interaction with time (p = 0.0099) when compared to the no flow treatment. Similarly, in the pairwise comparison, the high flow treatment exhibited a significantly steeper decline in eDNA concentration compared to the no flow (p = 0.0482), low flow (p < 0.001), and medium flow (p = 0.017) treatments. Pairwise comparisons indicated no significant differences between the no flow, low flow, and medium flow treatments.
4 Discussion
4.1 Low Rate of eDNA Degradation
The observed decay rate represents the rate at which measured eDNA concentrations change over time. This observed decay rate encompasses not only the degradation process, but also incorporates methodological factors (e.g., sample volume and PCR efficiency) and changes in the spatio-temporal distribution of eDNA. The no flow run provided a baseline for the level of eDNA degradation throughout the duration of the experiment. Notably, the overall degradation in this study is low relative to other published works (e.g., Kagzi et al. 2022; Wood et al. 2020). For instance, decay rate constants published by Kagzi et al. (2022) ranged between 0.0203 and 0.0348 h−1 (pH 7–10), whereas our no flow run presented an observed decay rate constant of 0.0033 h−1 over the total time series. The low level of degradation is unlikely to be an artifact of contamination, since the hydraulic laboratory does not house zebrafish, and both the extraction and amplification controls displayed negligible levels of contamination. As such, we speculate that the low level of degradation likely stems from a combination of factors.
Firstly, the low level of degradation may have been due to low microbe-mediated degradation resulting from our use of potable tap water. Microbial activity and abundance are known to play a significant role in the breakdown of eDNA (Strickler et al. 2015; Zhao et al. 2023). Potable tap water is known to contain low levels of bacterial diversity and low bacterial cell counts compared to surface water (Vargha et al. 2023). Similarly to the current study, Saito and Doi (2021) have previously noted significantly lower eDNA degradation rates when monitoring eDNA in purified water versus in sea or pond water.
Secondly, the low level of degradation may be due to the fact that the water temperature was relatively low (around 15°C) compared to previous eDNA degradation experiments (McKnight et al. 2024; Eichmiller et al. 2016), which may have decreased microbial metabolism. Temperature and eDNA degradation are positively correlated: microbial metabolism increases with increasing temperature (Strickler et al. 2015; Corinaldesi et al. 2008).
Thirdly, the low level of degradation may be associated with the relatively small assayed fragment sizes. This is because DNA damage follows a random Poisson process, causing decay rates to exponentially increase with increasing fragment size (Jo 2023). The selected COI marker (73 bp) is on the short end of the recommended size range of ddPCR assays (60–200 bp). The impact of target size on decay rates is still subject to further research, with studies showing both the impact of target size (e.g., Mikutis et al. 2019; Jo et al. 2017) or the absence thereof (e.g., Bylemans et al. 2018).
A fourth reason for the relatively low level of degradation could be the fact that smaller-sized ‘free’ extracellular eDNA particles, associated with higher degradation rates (Zhao et al. 2021), may have flushed through the filter pores. The filters utilized here selected for eDNA particles larger than 1.2 μm. Together, the listed reasons likely contributed to the reduced level of eDNA degradation. It is due to this reduced level of degradation that other mechanisms became more influential in the observed change in eDNA concentration over time.
4.2 Mechanisms That Govern the Observed eDNA Decay Rate
The statistical analysis of eDNA decay suggested a significant interaction between sampling time and the high flow treatment on the measured concentrations of eDNA. In addition, the post hoc Tukey's test found the high flow run to have a significantly higher observed decay rate constant compared to each of the other experimental runs. These differences cannot be attributed to methodological choices, since sampling strategies and analytical procedures were consistent between treatments. We hypothesize two main categories of mechanisms that may reduce or increase the observed eDNA concentration over time (Figure 5A). Mechanisms that may reduce the observed eDNA concentration over time (Figure 5B) include the dilution of the sampled section, eDNA degradation, eDNA particle aggregation, and the displacement of eDNA out from the sampled section.

Dilution is a significant factor for eDNA monitoring in river sections near tributaries and confluences. Dilution effects were nearly absent in our experimental runs. As mentioned before, only slight changes in experimental water volume occurred as a result of water sampling and evaporation, as well as the replacement of this water. eDNA degradation decreases the probability of recovery, as damage accumulates on the DNA strands. Assuming the eDNA degradation rate did not vary between the experimental runs, the lower level of eDNA degradation in our experiments increased the prominence of other mechanisms that affect the observed eDNA decay rate constant. The displacement of eDNA away from the sampled section may occur through either longitudinal, vertical, or transverse transport, or a combination thereof. Even though the eDNA was displaced longitudinally, the enclosed and circular nature of the flume ensured that eDNA could not be longitudinally displaced out of the sampled section. Any longitudinal discrepancies in eDNA distribution were covered by the longitudinally spaced subsampling strategy. The flume was well mixed laterally (Booij 1994), and displacement of eDNA due to lateral transport out of the sampled section is therefore considered to be unlikely. Displacement due to vertical transport, however, may have influenced our results, as water samples were consistently taken at half of the flow depth, which may overlook material settled at the flume bottom.
In the low flow run, eDNA was likely kept in suspension, leading to an observed decay rate constant that is indistinguishable from zero, aligning with the findings of Jane et al. (2015). Their experiment showed that higher flow rates were accompanied by higher eDNA concentrations over distance from the source. The authors argued that genetic material settles when exposed to low flow rates, decreasing the amount of available genetic material. Conversely, at high flows, genetic material was kept in suspension by upward, turbulent forces, keeping it available when sampling the water column. However, whereas Jane et al. (2015) found eDNA decay over distance to decrease with increasing flow, we observed a significant increase in the observed decay rate constant for the high flow run compared to each of the other cases.
A peak in eDNA concentration was observed during the first 48 h of the high flow experiment. Mechanisms that may increase the observed eDNA concentration over time (Figure 5C) include eDNA production, the reintroduction of eDNA into the sampled section through displacement (e.g., resuspension), elution of the sampled section, and fragmentation of eDNA particles. In our experiments, eDNA production was not a factor, as zebrafish were absent from the annular flume. Elution is also unlikely to have caused the peak, as the evaporation rate was too marginal to significantly impact the observed eDNA concentration over time. Displacement of eDNA into the sampled section may have occurred due to turbulence, causing upward movement of the eDNA particles. However, since the resuspension of organic matter typically occurs over the span of minutes, the extended duration of the peak suggests that it cannot be solely attributed to particle suspension.
Lastly, eDNA particle fragmentation pertains to the breakage of clusters of genetic material into smaller particles, followed by the dispersion or scattering of these fragmented particles across the experimental volume. We attribute this mechanism to shear stress acting upon eDNA particles under conditions of flow. This results in smaller and more uniformly distributed eDNA particles over the experimental volume, which increases the probability of eDNA detection. A first condition for eDNA particle fragmentation to lead to an increase in the observed eDNA concentration over time is a heterogeneous distribution of this material (e.g., Jerde et al. 2016; Nathan et al. 2014). A second condition is for the particles to have a size that is equal to or greater than the smallest scales of turbulent flow (i.e., the Kolmogorov length scale) in the system. This second condition was met in our experiments, as the approximated Kolmogorov length scales (47–152 μm; Section 2.3) were on the same scale or smaller than the majority of the measured particle sizes in the system (100–1000 μm; Section 3.1). A third condition is for the shear stress to be greater than the bonding strength of the relevant particles. The shear stress (0.1–2 Pa; Section 2.3) indeed exceeded the bonding strength (4.8 × 10−3 and 8.6 × 10−2 Pa; Section 3) of the eDNA particles in our experiments according to the model from Xiao et al. (2015). As a result, the particles could theoretically be sheared down to the Kolmogorov length scale.
It should be noted that the calculated bonding strength, however, is associated with uncertainty in capturing the bonding strength of eDNA aggregates. The model from Xiao et al. (2015) assumes a particle that is homogeneous in composition and structure, which our observations do not support. Furthermore, the model requires the identification of a representative primary particle size, as well as a fractal dimension in a given aggregate. The selection of such a representative primary particle size is challenging given the diverse states of eDNA (e.g., dissolved, particle bound, intraorganellar/-cellular).
van Driessche et al. (2023) and Stoeckle et al. (2021) have similarly observed a peak in eDNA concentrations under field conditions and have likewise attributed these peaks to the homogenization of eDNA (van Driessche et al. 2023; Stoeckle et al. 2021). Additional examples of increased particle detection frequencies can be found in other fields of research, where, for instance, organic matter (i.e., activated sludge) with particles sized between 150 and 180 μm broke down when subjected to similar levels of shear stress (~1–5 Pa) (Yuan and Farnood 2010). As reasoned above, due to the absence of alternative explanations, we suspect the dominant mechanisms in our experiments to have been the vertical displacement of eDNA, as well as the fragmentation of eDNA particles.
4.3 eDNA Decay Rates Under Field Conditions
The planning, execution, and analysis of these laboratory experiments involved various assumptions and abstractions that may limit their extrapolation to field scenarios. For the sake of simplicity, features of lotic systems such as variable flow rates and the presence of substrate were not included in our experiments. Lotic systems typically transport a broad range of particles alongside eDNA. Various studies have reported that the presence of particles with affinity to DNA molecules reduces their degradation rate and thereby extends their presence. This suggests that in field scenarios, the presence of, e.g., mineral particles would have likely influenced the results of this study. Moreover, these experiments made use of potable tap water as a medium. Potable tap water is known to house a microbial community that is poorer in abundance and diversity than riverine water. In our analysis, we also assumed similar degradation rates among our experimental runs. Yet, the flow rate is known to affect the composition and abundance of the microbial community. As a result, the rate of degradation may vary between runs and differ from rates of degradation in the field. The limited availability of natural light likely implies that UV-B radiation was reduced compared to field conditions, which could affect eDNA degradation rates. Finally, our results focus on a single species and therefore may not be applicable to species with different modes of eDNA shedding.
Considering the limitations mentioned above, our results indicate that observed eDNA decay rates retrieved from static controlled (laboratory or mesocosm) experiments do not represent the observed eDNA decay rates in highly dynamic environments. The applied flow velocities, pH, and temperature all fell within ranges that are present in field conditions. Given the investigated flow velocity range, our results indicate that eDNA particles may fragment under conditions of flow, a phenomenon that may also be found under field conditions. This change in the state of eDNA particles may have implications for the interpretation of eDNA detection. For instance, biomass approximations in dynamic environments based on detected eDNA quantities need to account for the case-specific hydrodynamics and eDNA degradation, as well as eDNA particle fragmentation due to shear stress. These findings encourage eDNA-based surveyors to account for spatial variability in eDNA signals, for instance by sampling across space.
5 Conclusion
Based on annular flume experiments under varying flow velocities, we find that flow-induced eDNA transport may increase the observed eDNA concentrations due to turbulent fluctuations that keep eDNA particles in suspension. A temporary peak in eDNA concentration was observed in the highest flow velocity experiment. This suggests that eDNA particles are fragmented and become more homogenized when subjected to conditions of shear stress.
Moreover, our findings show that eDNA decay rates retrieved from static mesocosm experiments do not represent the decay rates from dynamic environments. In our annular flume experiments, we observe that under high flow conditions, eDNA concentrations were likely affected by particle fragmentation. Therefore, an improved eDNA particle bonding strength model which captures the heterogeneous state of eDNA particles is of relevance for future studies on the impact of shear stress on eDNA detection probability. We encourage research on the stability of eDNA-mineral complexes under realistic shear stress ranges. Neglecting the heterogeneous distribution of eDNA may lead to inaccurate biomass estimations in river systems. Therefore, we recommend eDNA-based biomass estimates to account for the spatial heterogeneity in eDNA fragment distribution under conditions of flow.
Acknowledgments
This study was part of the project ‘DECODE-bioDivErsity estimate for aquatiC ecOsystems aDopting eDNA’ (TU09) which was funded by the ‘Topconsortium voor Kennis en Innovatie’ (TKI). The authors additionally acknowledge support from TU Delft internal funds through the Delta Transport Processes Laboratory. We thank the technicians of the Delft University of Technology for their support in the repair of the annular flume, as well as their support in the safe performance of the experiment. We would also like to thank the technicians of the zebrafish facility of Leiden University, specifically Guus van der Velden and Ulrike Nehrdich, for their assistance in the retrieval of the zebrafish rearing water.
Conflicts of Interest
The authors declare no conflicts of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




