Despite the close of a tumultuous 2020 and the start of 2021, connected devices will continue to shape the future of numerous industries, and businesses are confident that the Internet of Things (IoT) will play a key role in the future success of their trade. The growing Internet of Things (IoT) is connecting devices to a variety of sensors, applications, and other IoT elements to automate business processes and support human efficiencies in business and the home. WSN along with node localization algorithms can play a critical role in IoT applications. Nevertheless, in IoT applications, the context of real-time location-based services is gaining an overwhelming interest. To do this, several approaches are proposed in the recent literature based mainly on computational intelligence algorithms. This paper proposes a node localization algorithm based on swarm intelligence algorithms, that is, a hybrid Harris Hawks optimization based on differential evolution (HHODE).HHODE algorithm relies on Euclidian Distance as objective function to evaluate best-fit coordinates of sensor nodes in a wireless sensor network. Moreover, several experimentations are performed depending on the network size, communication range of sensors, geographical distribution, and the beacon nodes' density to demonstrate the efficiency of the HHODE algorithm. Compared to Standard DE, HOO, PSO, and Bat Algorithm, HHODE shows higher performance with regard to node localization.

1 INTRODUCTION

The Internet of Things (IoT) allows the connections of thousands of sensors, actuators, and smart devices for persisting connectivity, autonomously gathering, and sending information. The placement of the sensors is unnecessary predefined; they might be haphazardly distributed in a region known as the “sensing field,” which corresponds to the field of concern for the phenomena being observed.

The effective use of IoT networks or D2D communication¹ has offered up a bunch of emerging research fields like transportation, biological monitoring, wearable computing,² Crowd Dynamics Management,³ and so on where many problems are observed and treated in IoT Networks, like “energy consumption,^{4, 5} fault tolerance, scalability, deployment, and topology maintenance.”⁶

The most important challenge in IoT networks is node localization.⁷ In addition, the node localization is important in several fields and has received much attention in a variety of smart applications sectors such as water quality monitoring, intrusion detection, sniper localization, and health monitoring.

The fundamental purpose of node localization is estimating the nodes' positions from unknown location information employing the real positions' awareness of a small number of sensors and inter-sensor distances. The sensors with unknown location information are called non-anchor nodes where sensors with known location information are called anchor or beacons nodes. The aptitude to self-localize is particularly effective in environmental monitoring applications.

Solving the problem intuitively and easily providing every sensor with (GPS) devices remain ineffective for the following factors:

the device's expensive cost in matters of measurement, power, computing time, and area; and
service's low accuracy in specific settings (indoors, underground, etc.).

The more practical solution for this problem is to employ optimization approaches; furthermore, in Doherty et al.,⁸ convex optimization is presented as the first one to overcome with it.

The emerging tendency in processing with the node localization problem is using a small number of beacons and to call the communication methods presented in Kulkarni and Venayagamoorthy⁹ for the localization of unknown nodes rather than applying GPS, where the sensor network localization method will estimate their locations.

Newly, Hawks optimization based on differential evolution (HHODE) is proposed¹⁰ as a hybrid metaheuristic algorithm. In this paper, HHODE is proposed for the issue; HHODE is a hybridization of Harris' Hawk optimization algorithm¹¹ exploration phase with the differential evolution algorithm¹² to ensure a balance between exploration and exploitation. In addition, the proposed algorithm provides a large solution space to discover and to analyze optimal potential solutions among exploitation phase, and it clearly shows its effectiveness when it comes to localization time and error.

This paper is presented in eight sections. The overview of the node localization problem by a metaheuristic algorithm where related work is given in Section 2. Section 3 introduce the HHO algorithm, while the Section 4 presents the node localization problem based on HHODE algorithm. The performance evaluation and a comparative study are shown in the Section 5. The final section contains our conclusion.

2 RELATED WORK

Over the last few years, the localization of nodes has become very critical. The categorization of node localization is depending on various criteria:

The nodes' mobility.
The environment of deployment.
The distance estimation.
Network dimension.

Additionally, the system for localization can be defined into three phases combined. The main purpose of the step one is estimating the distance between anchor nodes and target nodes, despite the fact that several methods are employed and have been classified principally into two classes schematized in Figure 1.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Distance estimation algorithms

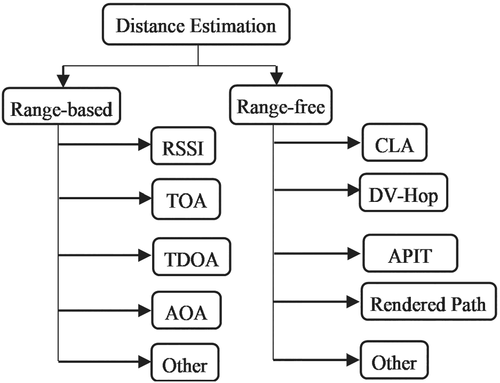
“Range-based uses the communication range for distance estimation to determine the nodes moreover at (2D)” as in Zhang et al.¹³ or more beacon nodes (3D) as in Ahmad et al.¹⁴ The most popular are as follows:

“Received Signal Strength Indicator (RSSI)”,¹⁵ “Angle Of Arrival (AOA)”,¹⁶ “Time Of Arrival (TOA)”,¹⁷ and “Time Difference Of Arrival (TDOA),”¹⁸ and recently other.¹⁹

Range-free based, instead, uses connection or proximity data to estimate distance. The generally used are “Distance Vector-Hop (DV-Hop),” “Approximate Point in Triangulation Test (APIT),” “Centroid Localization Algorithm (CLA),” “Rendered Path (RP),” and so on.²⁰

Distance estimation algorithms are chosen based on their impact on the system's performance, and each one is targeted to a certain application field.

RSSI is one of the most frequently used range-based methods. It is modeled as follows:

P_{r} (d) = P_{0} (d_{0}) - 10 η_{p} * \log_{10} (\frac{d}{d_{0}}) + X_{σ}

(1)

where

P_{r} (d)

is the received signal power,

P_{0} (d_{0})

“a given power value” at “a distance”

d_{0}

from the transmitter,

X_{σ}

“a zero mean Gaussian distributed random variable,”

η_{p}

“a path loss exponent measures how fast RSSI drops with distance.” Figure 2 presents the distance and signal strength at different levels.

The second step of the node localization scheme is position computation. With the data from the previous step, it's feasible to compute the locations of the target nodes. A lot of methods are used in this step like “trilateration (Figure 3A), multilateration (Figure 3C) and triangulation (Figure 3B),”²¹ “probabilistic approaches,”²² “bounding box,”²³ and “the central position and fingerprinting.”²⁴

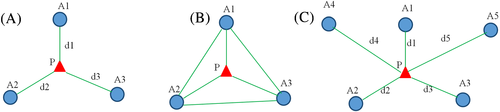
In the final step, for computing the target nodes' location using beacon nodes, a fusion scheme is realized between the two steps: distance estimation and position computation, as schematized in Figure 3.

Localization algorithms have received a considerable interest in the previous decade; primarily, mathematical techniques to deal with node localization problems are suggested.

Node localization is treated in Zhu et al.²⁵ by using maximum likelihood estimation. In previous studies,^{26, 27} two received signal strength indicator (RSSI) based approaches were developed where wireless sensors could find their position using WLAN technology in an indoor environment. The first approach uses a training session, and the position is based on neuronal networks using training measurements. The second approach uses triangulation model with some fixed access points.

Even if these traditional methods of operations research work well, huge computing efforts and overhead communication are required, which expand exponentially while the problem size grows. In addition, it is impossible to ensure the WSN's ability to manage growing sensor nodes, as well as to provide a very important localization time that will affect not only the power usage of the nodes but also the whole network.

Metaheuristic and swarm intelligence techniques have recently been seen as effective methods for dealing with the node localization problem, where a large amount of stochastic population-based approaches are addressed.

In 2008, particle swarm optimization (PSO) is proposed,²⁸ where the nodes in the square network that have not yet been found are located using data obtained by anchor nodes. This method has some significant drawbacks:

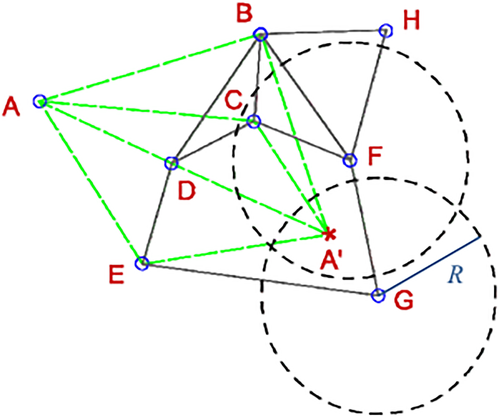
the flip ambiguity problem, schematized in (Figure 4) is neglect in this approach; and
the nodes communicate with the base station directly. So high communication range is needed.

In 2014, towards better performance, the Bat algorithm is presented.²⁹ According to the study results, the proposed algorithm's localization rate is extremely significant, and it is expected that Bat's rate is greater than BBO's. The Bat algorithm has shown that it is capable of solving the node localization issue, although the Bat algorithm suffers from a number of drawbacks:

localization time are not evaluated in this work; and
the Bat parameters chosen were not adjusted to the issue where the pulse rate is very high and maximum frequency is quite low.

In 2017, an effective Bat algorithm is introduced³⁰; the disadvantage of the original Bat algorithm is fixed with the Doppler effect phenomena. The simulations results show that the presented algorithm surpasses the Bat algorithm and particle swarm optimization (PSO) approaches.

In 2019, a new technique called moth-flame optimization algorithm (MFOA) has been suggested to overcome with the node localization problem.³¹ Moreover, the moth moves effectively via different trajectories, like the spiral trajectory. The simulation results indicate the efficiency of the algorithm.

For better accuracy, whale optimization algorithm (WOA)³² is addressed. WOA calculates node locations using multi stage method to traverse the entire network area. When applied to an enormous WSN, this method performs well with regard to node localization. The simulation results demonstrated WOA's superior performance in matters of localization error and computing time.

The salp swarm algorithm (SSA) was proposed to improve node localization.³³ It was compared to the particle swarm optimization, the firefly algorithm, the grey wolf optimization algorithm, and the Butterfly optimization algorithm. The simulation results demonstrate that the proposed method outperforms the other techniques.

In order to improve localization precision, dolphin swarm optimization (DSO)³⁴ was used to the M-curves' trajectory. The suggested route provides broad coverage and excellent position dependability. Despite this, the power usage was entirely ignored. When you browse the whole network using M-curves, you exhaust the mobile node, and the network goes down.

In 2020, an enhanced method based on Bat algorithms using a parallel position is proposed³⁵; the fundamental concept involves a central mobile node of some network nodes proceeding with a spiral trajectory for finding the nearby nodes. The simulation results show an outstanding localization quality in terms of accuracy and energy consumption.

An enhanced fruit fly optimization algorithm (EFFOA) is presented³⁶ for better node localization accuracy with swarm intelligence. The simulation results on different studies and situations show that EFFOA exceeds some famous optimization algorithms.

A new optimization approach known as the sine–cosine algorithm is proposed³⁷ to resolve the localization issue. The suggested approach resolves the problem of flip ambiguity. In terms of localization accuracy, the number of localized nodes and the speed of localization, the experimental results revealed good performance when compared to GWO, PSO, and GA algorithms.

In 2021, Nguyen et al.³⁸ present a novel hybrid swarm evolution method (HSEA) for node localization. The HSEA is constructed by mixing the particle swarm optimizer (PSO) and the differential-evolution (DE) algorithms. The simulation results of the proposed method shown that HSEA enhanced the efficiency in the matters of localization error and localized nodes' number than other algorithms.

In Nguyen et al.,³⁹ glowworms swarm optimization (GSO) was introduced for better localization accuracy. The objective function was stated mathematically by using a three dimensions localizing model's (3D) and Pareto distances. Outcomes show that GSO outperforms both PSO and CS algorithms.

In Dao et al.,⁴⁰ ant lion optimizer (ALO) was developed to solve localization issue. In the tests, the impacts of parameters such as node density and communicating range are evaluated in order to evaluate the effectiveness of the proposed technique in terms of mean localization error and percentage of success. When compared to the results of the tests with cuckoo search (CS) and particle swarm optimization (PSO), the proposed approach clearly outperforms the competition in terms of location accuracy.

A new technique to localization in WSNs utilizing the KH algorithm has been suggested.⁴¹ Trilateration is used to compute the non-anchor node positions. In terms of accuracy and error, the performance evaluation revealed that the KH-based localization algorithm outperforms PSO and IAL algorithms.

For greater accuracy with swarm intelligence, Hawks optimization algorithm (HHO) is proposed.⁴² The simulations results show that the algorithm surpasses some approaches in computation cost and accuracy.

3 HARRIS' HAWK OPTIMIZATION (HHO)

Harris Hawks optimization (HHO) is a population-based, gradient-free optimization technique proposed in Birogul,¹⁰ “ it is based on Harris Harris' Hawk's strategy in catching its prey, where certain Hawks attack from various angles the selected target in coordination for instant disorientation. The goal is to reach the prey neatly. The attack should be done within seconds. Nevertheless, in some cases, based on the prey's getaway power and tracking territory, the objective can be achieved in a brief time and with a huge amount of attacks. There is a leader during the coordinated attack. A new Harris' Hawk will take up the leadership if the first one becomes exhausted while chasing the prey or during the attack. Thus, Attacks continue in this manner until the hunt is successful or until prey escapes. This is a strategy that is sometimes employed. To confuse and tire the prey, it is necessary to attack from many directions at the same time. The operation is done when Harris' Hawk, the leader of the hunt, easily chases down the exhausted prey.” Figure 5 shows all steps and process of HHO, which are presented in the next subsection.

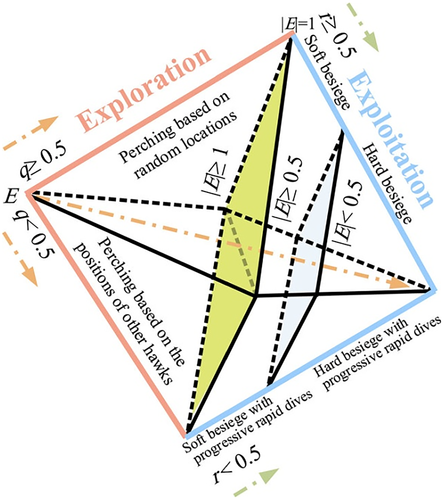
3.1 Exploration

In HHO, Harris' Hawks perch randomly on some locations and wait to detect a prey based on two strategies.

X (t + 1) = \{\begin{matrix} X_{rand} (t) - r_{1} |X_{rand} (t) - 2 r_{2} X (t)| q \geq 0.5 \\ (X_{rabbit} (t) - X_{m} (t)) - r_{3} (LB + r_{4} (UB - LB)) q < 0.5 \end{matrix}

(2)

where the two perching states are (q); in case of q < 0.5 the Hawk perches randomly according to the prey's (rabbit) position, and in the case of q ≥ 0.5 it does so according to other Hawks' positions in the hunting area. “X(t + 1) is the position vector of hawks in the next iteration t, X_rabbit(t) is the position of rabbit, X(t) is the current position vector of hawks, r₁, r₂, r₃, r₄, and q are random numbers inside (0,1), which are updated in each iteration, LB and UB show the upper and lower bounds of variables, X_rand(t) is a randomly selected hawk from the current population, and X_m is the average position of the current population of hawks. The average position of hawks is attained” using Equation (3):

X_{m} (t) = \frac{1}{N} \sum_{I = 1}^{N} X_{i} (t)

(3)

where X_i(t) is “the position of each hawk in iteration t” and N is “the total number of hawks.”

3.2 Transition from exploration to exploitation

To represent this phase, the power of a rabbit is represented as

E = 2 E_{0} (1 - \frac{t}{T})

(4)

where E is “the prey's getaway power,” T represent “the maximum number of iterations,” and E₀ represent “the initial state of its power.”

3.3 Exploitation phase

3.3.1 Soft besiege

The rules that model this behavior are as follows:

EX (t + 1) = ∆ X (t) - E |J X_{rabbit} (t) - X (t)|

(5)

∆ X (t) = Xrabbit (t) - X (t)

(6)

∆X(t) is “the difference between the position vector of the rabbit and the current location in iteration t,” $r_{5}$ is a “random number inside (0,1),” and “J = 2 (1 − $r_{5}$ )” represents “the random jump strength of the rabbit throughout the escaping procedure.” The J value changes randomly in each iteration to simulate the nature of rabbit motions.

3.3.2 Hard besiege

In the present case, the current positions are updated using Equation (7):

X (t + 1) = X_{rabbit} (t) - E ∣ ∆X (t) ∣

(7)

3.3.3 Soft besiege with progressive rapid dives

To accomplish a soft besiege, hawks are expected to make their next action depending on the following rule in Equation (8):

Y = X_{rabbit} (t) - E ∣ {JX}_{rabbit} (t) - X (t) ∣

(8)

The hawks will dive according to the LF-based patterns using the following rule in Equation (9):

Z = Y + S \times LF (D)

(9)

where D is “the dimension of the problem” and S is “a random vector by size 1 × D” and LF is “the levy flight function,” which is calculated using Equation (10):

LF (x) = 0.01 \times \frac{u \times σ}{{|v|}^{\frac{1}{β}}}, σ = {(\frac{Γ (1 + β) \times \sin (\frac{πβ}{2})}{Γ (\frac{1 + β}{2}) \times β \times 2^{(\frac{β - 1}{2})}})}^{\frac{1}{β}}

(10)

where $u$ , $v$ are “random values inside (0,1),” $β$ is “a default constant set to 1.5.”

As a result, the last tactic for actualizing hawk positions during the soft besiege phase can be carried out by Equation (11):

X (t + 1) = \{\begin{matrix} Y if F (Y) < F (X (t)) \\ Z if F (Z) < F (X (t)) \end{matrix}

(11)

where Y and Z are obtained using Equations (8) and (9).

3.3.4 Hard besiege with progressive rapid dives

The following rule is performed in hard besiege condition:

X (t + 1) = \{\begin{matrix} Y if F (Y) < F (X (t)) \\ Z if F (Z) < F (X (t)) \end{matrix}

(12)

where Y and Z are obtained using new rules in Equations (13) and (14).

Y = X_{rabbit} (t) - E ∣ {JX}_{rabbit} (t) - X_{m} (t) ∣

(13)

Z = Y + S \times LF (D)

(14)

where Xm(t) is obtained using Equation (3). The pseudo code of the classic HHO is given in Figure 6.

4 NODE LOCALIZATION BY HARRISON HAWK OPTIMIZATION BASED ON DIFFERENTIAL EVOLUTION ALGORITHM (HHODE)

HHODE proposed in Birogul¹⁰ is a hybridization of Harris' Hawk optimization algorithm¹¹ exploration phase with the differential evolution algorithm. DE algorithm is a basic strong population based method applied to global optimization functions that carry real parameters. DE utilizes a mutation mechanism based on the differences of randomly chosen objective vector pairs. This increases its speed and makes it powerful. In addition, DE algorithm gives a fast, readily, simply means and that is modified easily for developing hybrid algorithms. It is readily applied to integer, discrete, and mixed parameter optimization, sometimes employed for functions linked to time/iteration, also provide alternative solutions in a single run and has successful particularly in nonlinear constrained optimization situations. In the operating procedure of DE, x is the solution that is disturbed like random or best; y is “the number of difference vectors” utilized to perturb x. Each difference vector represents the difference between two (randomly) chosen yet different “population members. z indicates the recombination operator employed such as binomial (bin) or exponential (exp).”⁴³ “The five mutation types frequently employed in the DE method were provided in the following equations.”^{44, 45}

DE / rand / 1; V_{i}^{g} = X_{r 1}^{g} + F . X (X_{r 2}^{g} - X_{r 3}^{g})

(15)

DE / best / 1; V_{i}^{g} = X_{best}^{g} + F (X_{r 1}^{g} - X_{r 2}^{g})

(16)

DE / current - to - best / 2; V_{i}^{g} = X_{i}^{g} + F (X_{best}^{g} - X_{i}^{g} + X_{r 1}^{g} - X_{r 2}^{g})

(17)

DE / best / 2; V_{i}^{g} = X_{best}^{g} + F (X_{r 1}^{g} - X_{r 2}^{g} + X_{r 3}^{g} - X_{r 4}^{g})

(18)

DE / rand / 2; V_{i}^{g} = X_{r 1}^{g} + F (X_{r 2}^{g} - X_{r 3}^{g} + X_{r 4}^{g} - X_{r 5}^{g})

(19)

“Mutation generated for each

X_{I}

within the

V_{I}

V_{i}^{1}

V_{i}^{2}

… …

V_{i}^{N}

) population which appears inside these formulas is a vector.

r_{1}

r_{2}

r_{3}

r_{4}

, and

r_{5}

values are random numbers generated between population size (NP) and 1. F, scale vector and

X_{best}

are the value X, which indicates the probable solution that has the best conformity value. The DE binomial crossover operator that is used is defined in Equation (20). In this equation,

u_{I}

is the produced offspring and CR is the crossing rate, and g is the scalling factor generated independent from

X_{I}

. Cauchy distribution is made according to

F_{I}

=Cauchy (lop,0.1). The value of

F_{I}

is regenerated if

F_{I}

<0 or

F_{I}

> 1. The crossover rate is generated under anormal distribution

{CR}_{I}

=normal (CR,0.1).”⁴⁴

u_{i} = \{\begin{matrix} v_{i}, if (with probabilty of CR) \\ X_{i}, otherwise \end{matrix}

(20)

The DE mutation operators were incorporated in the HHO algorithm's exploration stage. At this step of HHO, each Hawk is placed in a random position and waits to locate the prey according to two scenarios. Assuming that these two perching states are (q); in the event of 𝑞 < 0.5, the Hawk perches according to the prey (rabbit) the location, and in the case of 𝑞 > 0.5, according to other Hawks' position situated in the hunting region. The case of 𝑞 > 0.5, in computation of (𝑡 + 1), HHODE structure is obtained by employing five mutation operators of DE, only arbitrarily applying one of these mutation operators will be sufficient to apply.

“The HHODE controls an overall population space which is shared by HHO and DE. The differential evolution (DE) optimization has the benefit that, in the course of local search, the diversity in the population”. The pseudo code of the HHODE is given in Figure 7.

The node localization is determining the positions of maximum unknown nodes based on the minimum of beacon nodes with a one hop based range in a distributed network (Figure 8). The following are the major steps in the node localization system based on HHODE:

random deployment of N beacon nodes and M unknown nodes, with the same range of communication;
the beacon nodes compute the locations and send their positions using RSSI;
localized nodes are defined as nodes that are encircled by three or more beacons;
the localized node computes its distance $d_{i}$ to every neighboring beacons. An actual distance between the target node $(x$ , $y)$ and i^th beacon ( $x_{i}$ , $y_{i}$ ) is described as

d_{i} = \sqrt{{(x - x_{i})}^{2} + {(y - y_{i})}^{2}} .

(21)

Due to environmental constraints, the distance estimation is generally impacted by many paths and obstacles blocking the way. It's expressed as “noise”

n_{i}

. The measured distance”

{\hat{d}}_{i}

is modeled as follows:

{\hat{d}}_{i} = [d_{i} + n_{i}]

(22)

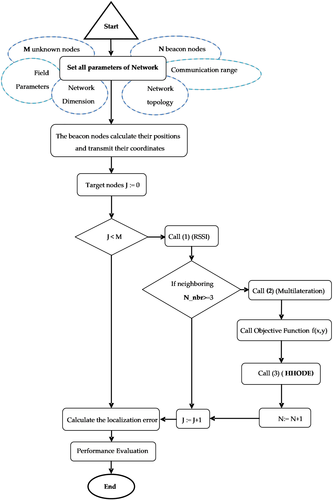
Each localized node autonomously runs HHODE to determine its location by computing its positions (x, y). The objective function (mean square error between actual node positions and estimated distances) is computed as follows:

f (x, y) = \frac{1}{N} \sum_{i = 1}^{N} \sqrt{{(x - x_{i})}^{2} + {(y - y_{i})}^{2}} - {\hat{d}}_{i}

(23)

where N ≥ 3 (2 D the node's location necessitates the use of at least three beacon nodes.)

At every iteration end, nodes that have been founded perform as beacon nodes in the following iteration. This decreases the probability of the flip ambiguity.
The steps 2 to 6 repeated by a number of iteration defined or until all target nodes get localized or no more nodes can be localized. The mean localization error (MLE) is computed as the mean square of Euclidean distance so of computed node coordinates ( $x_{i}, y_{i}$ ) and the actual node coordinates ( $X_{i}, Y_{i}),$ for i = 1,2, …. ML determined for HHODE algorithm, as shown below:

E_{L} = \frac{1}{M_{L}} \sum_{i = 1}^{L} \sqrt{{(x_{i} - X_{i})}^{2} + {(y_{i} - Y_{i})}^{2}}

(24)

where “L = M – N.”

5 SIMULATION EXPERIMENTS AND PERFORMANCE EVALUATION

Several parameters have been examined to evaluate HHODE's performance like: population size, convergence of the algorithm, anchor density, communication range, Moreover, a comparative study is done with some metaheuristics as Standard DE, HOO, PSO, and Bat Algorithm by providing various criteria.

5.1 The main standards

The main standards⁴⁶ used to evaluate the performance are:

5.1.1 Mean localization errors (MLE)

The mean distance between the estimated location ( $x_{i}, y_{i}$ ) and the real node coordinates ( $X_{i}, Y_{i})$ .

E_{L} = \frac{\sum_{i = 1}^{L} \sqrt{{(x_{i} - X_{i})}^{2} + {(y_{i} - Y_{i})}^{2}}}{M_{L}}

(25)

5.1.2 Mean computing time (MCT)

The average time necessary to locate all sensors

Mean Computing Time = \frac{\sum_{i = 1}^{n} excution time}{n (number of sensor node)}

(26)

5.2 Simulation setup

In this subsection, all the simulations are performed using MATLAB environment on a laptop of 8 GB memory and i5-2.4 GHz CPU to evaluate the performance of HHODE. In our simulation experiments, the sensor nodes are randomly deployed over a 50 m x 50 m meters square area. The number of sensors is 200 where 40 anchor nodes are taken. The transmission range of sensor node is 30 m. The initial deployment of sensor node is random, in each iteration; the number of localizable nodes is not expected to be the same. The unknown nodes' coordinates are calculated using HHODE.

5.3 Evaluation parameters of HHODE

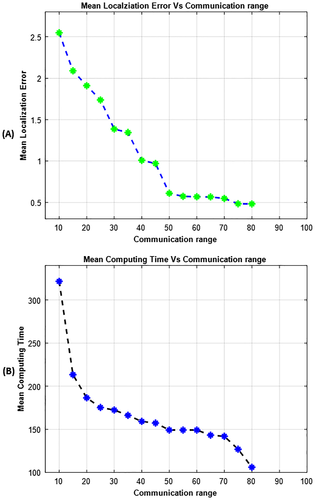
5.3.1 The effect of communication range

The communication range specifies whether or not unknown nodes are covered by the beacon nodes and having more than three beacon nodes around them, which is one of the most essential parameters. The obtained result is depicted in the following figures. From Figure 9A, it is observed that for a range less than 20, the localization error is insignificantly high. The phenomenon can be explained by the nodes are scattered in the networks, and the connectivity is low also depends on the preliminary deployment. On the other hand, we perceive that the communication range is over 20, make the localization error decline; as the result, there is more anchor information to compute the position of unknown nodes. Although at a certain value of the range, the localization error gradually declines. From the localization time versus communication range shown in Figure 9B, we see that the algorithm convergence rapidly; this is because, in the case of a little communication range, the unknown nodes are quickly localized by the beacon nodes with a major error. The greater the communication range is, the lengthy the computing time will be. The environmentally noise affects the unknown node as well the localization error. In conclusion, the computing time is excellent and with the suitable communication range, which keeps the power usage low.

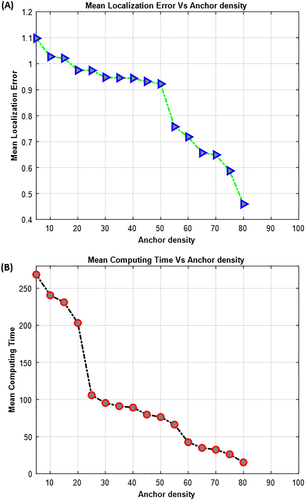
5.3.2 The effect of anchor density

The beacon nodes' density as an important parameter affects the localization performance and the wireless sensor network cost. To evaluate this effect, various experiments were conducted. Figure 10A show the localization error versus anchor density. It showed up that the MLE progressively reduced according to the progression of density; once the density increments, the network connectivity is high. On the other hand, we can see from Figure 10B that localization time reduces as the number of anchor nodes increase, this is because additional localized nodes become anchor nodes at each iteration, reducing the number of unknown nodes.

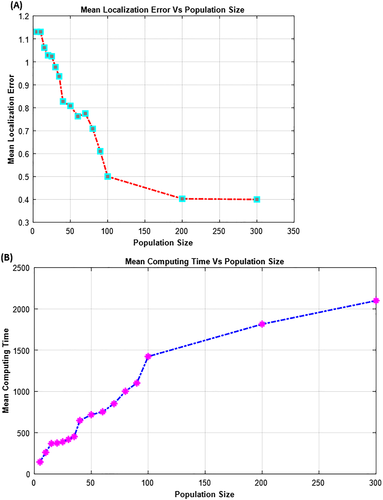
5.3.3 The effect of population size

The population size is an important determinant in the algorithm's convergence, especially during the exploration phase. Moreover, a study of the localization problem with population size variations was performed (communication range = 30, number of iteration number = 30 iteration and anchor density is 20 sensor nodes). In Figure 11A the simulation results indicate the fast convergence of the algorithm when the population rate is high, which advantages the algorithm in the exploration phase. Furthermore, Figure 11B show that the localization error is inversely related to the computing time. Because hawks were involved in determining the global minimum values of optimal positions for unknown nodes, As a result of this, the network is able to maintain its energy consumption and optimize its lifetime.

5.4 Comparative study

In this sub-section, a descriptive analysis is simulated and examined of “HHODE,” with Standard DE, HOO, PSO, and Bat Algorithm. The nodes' deployment is shown in Figure 12, and the number of nodes is 200 nodes, deployed in random way in 50 m × 50 m (two-dimension) network space with 40 beacon nodes.

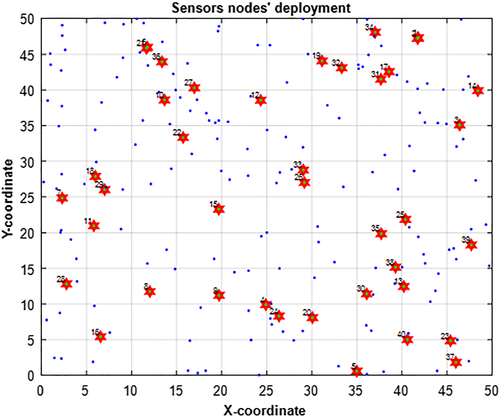
Figure 13A illustrates the progression of HHODE in terms of localization error with other meta-heuristics. The simulations demonstrate that the minimal localization error is reached by HHODE. The presented algorithm very easily converges and gives the ideal result, especially with the increases of iterations. HHODE gives high accuracy position relatively to other meta-heuristic algorithms. In addition, Figure 13B presents the variation of localization time, where every algorithm run-time is calculated regarding iteration number. Calculations are totally carried out on the unique system in seconds. From the above we conclude that a minimal calculation let the HHODE determines maximal unknown nodes' location in few iterations in comparison to other algorithms.

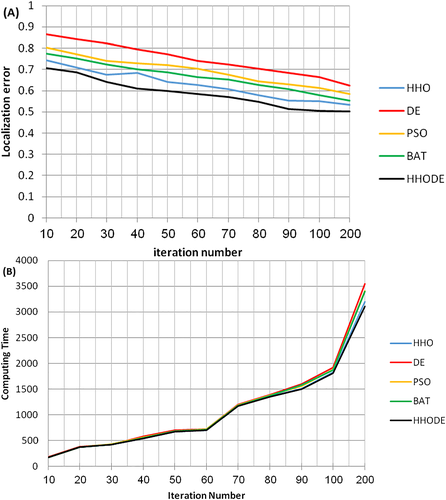
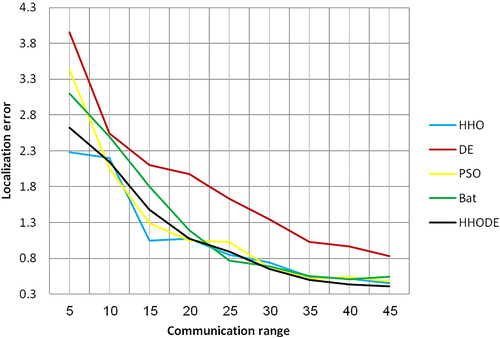
Figure 14 represents the variations of localization error according to communication range. We see that the localization error obtained by DE is very high compared to other algorithms. When communication range is over 30, HHODE outperform the others algorithms and gives the smallest localization errors, this due that the HHODE algorithm is able to show high and competitive exploration and exploitation functions.

6 CONCLUSION

In order to utilize the distance in node localization in WSN with higher ranging accuracy, an multilateration location-based metaheuristic (HHODE) algorithm is proposed.

Compared to popular swarm intelligence approaches like Standard DE, HOO, PSO, and Bat algorithm, the proposed algorithm has improved location accuracy and time response.

Several experiments have been carried out varying relevant network parameters such as network size, number of beacon nodes, and communication range of nodes.

Such experiments have proven a higher localization node accuracy as well as time response. This latter property of time response is critical in real-time application in an IoT infrastructure.

In the case of large environmental disturbance, it needs to adopt efficient corresponding methods to solve the problem of node localization. Node layout research based on two-dimensional level has limited application scope. Gradually realizing efficient location in three-dimensional level will play a greater role in intelligent buildings, large shopping malls and other scenarios.

Future works will emphasize on multiobjective optimization scheme in three-dimensional scenario by considering power consumption and scalability of the network in order to improve the network lifetime.

Furthermore, security aspects must be taken care of when dealing with node localization.

Fake position coordinates can be easily provided by a malicious beacon node. Resilient schemes have to be developed to overcome vulnerability in mobile wireless sensor networks.

Open Research

DATA AVAILABILITY STATEMENT

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

REFERENCES

1Liu J, Nishiyama H, Kato N, Guo J. On the outage probability of device-to-device-communication-enabled multichannel cellular networks: an RSS-threshold-based perspective. IEEE Journal on Selected Areas in Communications. 2016; 34(1): 163-175. doi:10.1109/jsac.2015.2452492
10.1109/jsac.2015.2452492
CAS Web of Science® Google Scholar
2Adnan MA, Abdur Razzaque M, Ahmed I, Isnin IF. Bio-mimic optimization strategies in wireless sensor networks: a survey. Sensors (Basel). 2013; 14(1): 299-345. doi:10.3390/s140100299
10.3390/s140100299
PubMed Google Scholar
3Kawamoto Y, Yamada N, Nishiyama H, Kato N, Shimizu Y, Zheng Y. A feedback control-based crowd dynamics management in IoT system. IEEE Internet Things J. 2017; 4(5): 1466-1476. doi:10.1109/jiot.2017.2724642
10.1109/jiot.2017.2724642
Web of Science® Google Scholar
4Guo H, Liu J, Zhang J, Sun W, Kato N. Mobile-edge computation offloading for ultradense IoT networks. IEEE Internet Things J. 2018; 5(6): 4977-4988. doi:10.1109/JIOT.2018.2838584
10.1109/JIOT.2018.2838584
Web of Science® Google Scholar
5Gupta V, De S. SBL-based adaptive sensing framework for WSN-assisted IoT applications. IEEE Internet Things J. 2018; 5(6): 4598-4612. doi:10.1109/jiot.2018.2870970
10.1109/jiot.2018.2870970
Web of Science® Google Scholar
6Mao G, Fidan B, Anderson BDO. Wireless sensor network localization techniques. Computer Networks. 2007; 51(10): 2529-2553. doi:10.1016/j.comnet.2006.11.018
10.1016/j.comnet.2006.11.018
Web of Science® Google Scholar
7Saad E, Elhosseini M, Haikal AY. Recent achievements in sensor localization algorithms. Alex Eng J. 2018; 57(4): 4219-4228. doi:10.1016/j.aej.2018.11.008
10.1016/j.aej.2018.11.008
Web of Science® Google Scholar
8Doherty L, Pister KSJ, Ghaoui LE. Convex Position Estimation in Wireless Sensor Networks. CiteSeer. 2001. Accessed September 15, 2021. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.409.816
10.1109/INFCOM.2001.916662
Google Scholar
9Kulkarni RV, Venayagamoorthy GK. Bio-inspired algorithms for autonomous deployment and localization of sensor nodes. IEEE Transactions on Systems, Man, and Cybernetics, Part C (Applications and Reviews). 2010; 40(6): 663-675. doi:10.1109/tsmcc.2010.2049649
10.1109/tsmcc.2010.2049649
Google Scholar
10Birogul S. Hybrid Harris Hawk optimization based on differential evolution (HHODE) algorithm for optimal power flow problem. IEEE Access. 2019; 7: 184468-184488. doi:10.1109/access.2019.2958279
10.1109/ACCESS.2019.2958279
Web of Science® Google Scholar
11Heidari AA, Mirjalili S, Faris H, Aljarah I, Mafarja M, Chen H. Harris Hawks optimization: algorithm and applications. Future Generation Computer Systems. 2019; 97: 849-872. doi:10.1016/j.future.2019.02.028
10.1016/j.future.2019.02.028
Web of Science® Google Scholar
12Storn R, Price K. Journal of Global Optimization. 1997; 11(4): 341-359. doi:10.1023/a:1008202821328
10.1023/a:1008202821328
Web of Science® Google Scholar
13Zhang Y, Liang J, Jiang S, Chen W. A localization method for underwater wireless sensor networks based on mobility prediction and particle swarm optimization algorithms. Sensors. 2016; 16(2): 212. doi:10.3390/s16020212
10.3390/s16020212
CAS Web of Science® Google Scholar
14Ahmad T, Jun Li X, Seet B-C. Parametric loop division for 3D localization in wireless sensor networks. Sensors. 2017; 17(7): 1697. doi:10.3390/s17071697
10.3390/s17071697
Web of Science® Google Scholar
15Hoang QT, Le Tan N, Shin Y. An RSS comparison based localization in wireless sensor networks. In: 8th Workshop on Positioning Navigation and Communication (WPNC); 2011: 116-121.
10.1109/WPNC.2011.5961026
Google Scholar
16Yanping Z, Daqing H, Aimin J. Network Localization Using Angle of Arrival. International Conference on Electro Information Technology; 2008: 205-210.
Google Scholar
17Shen G, Zetik R, Yan H, Hirsch O, Thomä S. Time of arrival estimation for range based localization in UWB sensor networks. In: Proc. of IEEE Int. Conf. on Ultra-Wideband (ICUWB). Vol. 2; 2010: 1-4.
10.1109/ICUWB.2010.5614041
Google Scholar
18Bahl P, Padmanabhan V N, RADAR: an in-building RF based user location and tracking system, in Proceedings of the 19th Annual Joint Conference of the IEEE Computer and Communications Societies, pp. 775–784, March 2000.
10.1109/INFCOM.2000.832252
Google Scholar
19Akyildiz I F, Vuran M C, Wireless Sensor Network, John Wiley & Sons, London, UK, 2010. doi:10.1002/9780470515181
10.1002/9780470515181
Google Scholar
20Adeniran A, Verdicchio F. Reach centroid localization algorithm. Wireless Sensor Network. 2017; 9(02): 87-101. doi:10.4236/wsn.2017.92005
10.4236/wsn.2017.92005
Google Scholar
21Farid Z, Nordin R, Ismail M, Recent advances in wireless indoor localization techniques and system, Journal of Computer Networks and Communications, 2013, 12. doi:10.1155/2013/185138
10.1155/2013/185138
Google Scholar
22Ramadurai V, Sichitiu ML. Localization in wireless sensor networks: a probabilistic approach. In: Proc. ICWN. Las Vegas; 2003: 275-281.
Google Scholar
23Simic S, Sastry S. Distributed localization in wireless ad hoc networks.
Google Scholar
24Wang X, Lingjun G, Shiwen M, Santosh P. CSI-based fingerprinting for indoor localization: a deep learning approach. IEEE Trans Veh Tech. 2017; 66: 763-776.
CAS Web of Science® Google Scholar
25Zhu J, Chen Q, Zhang J. Localization optimization algorithm of maximum likelihood estimation based on received signal strength. 9th IEEE International Conference on Communication Software and Networks. 2017; 830-834.
Google Scholar
26Garcia M, Martinez C, Tomas J, Lloret J. Wireless sensors self-location in an indoor WLAN environment. In: 2007 International Conference on Sensor Technologies and Applications (SENSORCOMM). Valencia, Spain; 2007.
10.1109/SENSORCOMM.2007.4394912
Google Scholar
27Garcia M, Tomas J, Boronat F, Lloret J. The development of two systems for indoor wireless sensors self-location. Ad Hoc Sens Wirel Networks. 2009; 8(3-4): 235-258.
Web of Science® Google Scholar
28Gopakumar A, Jacob L. Localization in wireless sensor networks using particle swarm optimization. In: International Conference on Wireless, Mobile and Multimedia Networks. Beijing, China; 2008: 227-230.
10.1049/cp:20080185
Google Scholar
29Goyal S, Patterh MS. Performance of Bat algorithm on localization of wireless sensor network. International Journal of Computers & Technology. 2013; 6(3): 351-358. doi:10.24297/ijct.v6i3.4481
10.24297/ijct.v6i3.4481
Google Scholar
30Mihoubi M, Rahmoun A, Lorenz P, Lasla N. An effective Bat algorithm for node localization in distributed wireless sensor network. Security and Privacy. 2017; 1(1):e7. doi:10.1002/spy2.7
10.1002/spy2.7
Web of Science® Google Scholar
31Miloud M, Abdellatif R, Lorenz P. Moth flame optimization algorithm range-based for node localization challenge in decentralized wireless sensor network. International Journal of Distributed Systems and Technologies. 2019; 10(1): 82-109. doi:10.4018/ijdst.2019010106
10.4018/ijdst.2019010106
Web of Science® Google Scholar
32Baidar L, Rahmoun A, Lorenz P, Mihoubi M. Whale optimization approach for optimization problem in distributed wireless sensor network. Proceedings of the 9th International Conference on Information Systems and Technologies. 2019. doi:10.1145/3361570.3361594
10.1145/3361570.3361594
Google Scholar
33Kanoosh HM, Houssein EH, Selim MM. Salp swarm algorithm for node localization in wireless sensor networks. Journal of Computer Networks and Communications. 2019; 2019: 1-12. doi:10.1155/2019/1028723
10.1155/2019/1028723
Web of Science® Google Scholar
34Kannadasan K, Edla DR, Kongara MC, Kuppili V. M-Curves path planning model for mobile anchor node and localization of sensor nodes using dolphin swarm algorithm. Wireless Networks. 2019; 26(4): 2769-2783. doi:10.1007/s11276-019-02032-4
10.1007/s11276?019?02032?4
Web of Science® Google Scholar
35Mihoubi M, Rahmoun A, Lorenz P. An enhanced Bat algorithm for parallel localization based on a mobile beacon sensor in wireless sensor networks. In: S Thampi, ed. Applied Soft Computing and Communication Networks. ACN 2019. Lecture Notes in Networks and Systems. Vol. 125. Singapore: Springer; 2020.
10.1007/978-981-15-3852-0_4
Google Scholar
36Mihoubi M, Rahmoun A, Zerkouk M, Lorenz P, Baidar L. Intelligent technique based on enhanced metaheuristic for optimization problem in Internet of Things and wireless sensor network. International Journal of Grid and High Performance Computing (IJGHPC). 2020; 12(3): 17-42. doi:10.4018/IJGHPC.2020070102
10.4018/IJGHPC.2020070102
Web of Science® Google Scholar
37Hamouda E, Abohamama AS. Wireless sensor nodes localiser based on sine–cosine algorithm. IET Wirel Sens Syst. 2020; 10(4): 145-153. doi:10.1049/iet-wss.2019.0163
10.1049/iet-wss.2019.0163
Web of Science® Google Scholar
38Nguyen TT, Sung TW, Pham DT, Ngo TG, Vu VD. (2021) A hybrid swarm evolution optimization for solving Sensornet node localization. In: DT Tran., G Jeon., TDL Nguyen, J Lu., TD Xuan. (eds) Intelligent Systems and Networks. ICISN 2021. Lecture Notes in Networks and Systems, vol 243. Springer, Singapore. doi:10.1007/978-981-16-2094-2_13
10.1007/978?981?16?2094?2_13
Google Scholar
39Nguyen T-T, Yu J, Nguyen, T-T-T, Kien D, Giang N. (2021). A solution to sensor node localization using glow-worm swarm optimization hybridizing positioning model 10.1007/978-981-33-6757-9_33.
Google Scholar
40Dao T-K, Pan J-S, Nguyen T-T, Chu S.C., Tran H.T., Nguyen T.D., Vu N.T. Node localization in wireless sensor network by ant lion optimization. Advances in Smart Vehicular Technology, Transportation, Communication and Applications. Published Online 2021: 97-109. doi:10.1007/978-981-16-1209-1_10
10.1007/978?981?16?1209?1_10
Google Scholar
41Sabbella VR, Edla DR, Lipare A, Parne SR. An efficient localization approach in wireless sensor networks using Krill Herd optimization algorithm. IEEE Systems Journal. 2021; 15(2): 2432-2442. doi:10.1109/jsyst.2020.3004527
10.1109/jsyst.2020.3004527
Web of Science® Google Scholar
42Mihoubi M, Rahmoun A, Lorenz P, Node localization in WSN and IoT using Harris Hawks optimization algorithm, 2021. IEEE Global Communications Conference (GLOBECOM), pp. 01-06. doi:10.1109/GLOBECOM46510.2021.9685105.
10.1109/GLOBECOM46510.2021.9685105
Google Scholar
43Kamaruzaman AF, Zain AM, Yusuf SM, Udin A. Levy flight algorithm for optimization problems—a literature review. Appl Mech Mater. 2013; 421: 496-501. doi:10.4028/www.scientific.net/amm.421.49
10.4028/www.scientific.net/amm.421.49
Google Scholar
44Awad NH, Ali MZ, Suganthan PN, Reynolds RG. CADE: a hybridization of cultural algorithm and differential evolution for numerical optimization. Inform Sci. 2017; 378: 215-241. doi:10.1016/j.ins.2016.10.039
10.1016/j.ins.2016.10.039
Web of Science® Google Scholar
45Qin K, Suganthan PN. Self-adaptive differential evolution algorithm for numerical optimization. IEEE Congr Evol Comput. 2005; 1785-1791.
Google Scholar
46Abdi F, Haghighat AT. A hybrid RSSI based localization algorithm for WSN using a mobile anchor node. In: International Conference on Computing, Communication and Networking Technologies, China; 2014.
10.1109/ICCCNT.2014.6963058
Google Scholar

Volume35, Issue9

June 2022

e5129

A hybrid Harrison Hawk optimization based on differential evolution for the node localization problem in IoT networks

Summary

1 INTRODUCTION

2 RELATED WORK