Taylor Bubble Study of the Influence of Fluid Dynamics on Yield and Selectivity in Fast Gas-Liquid Reactions 

1 Introduction

In times of scarcity of resources and increasing environmental awareness, a lot of attention is given to the optimization of large-scale processes in chemical industry, which make up about 20 % of the yearly total energy consumption ¹. Reactive multiphase flows occur for instance in oxidation, hydrogenation, and chlorination processes, where a gas phase is solved in a liquid and subsequently reacts with at least one of the liquid solutes. Such reactions are complex and undesired side- or by-products (S) can be formed. A simple model example of a fast competing consecutive gas-liquid reactions could follow the Eqs. 1 and 2, where A and B represent the liquid and gaseous educts and P the intermediate product

()

()

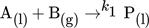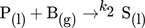The reaction kinetics k and mass transfer determine whether the reaction takes place directly in the boundary layer or in the liquid phase. For the applied model reaction, a clear distinction of these mechanisms is still part of further investigations. The efficiency of a process can be described by the yield and the selectivity. Both quantities depend on local mass transfer processes, i.e., fluid dynamics and reaction kinetics that affect each other ^2-6. For a better understanding of the interplay of fluid dynamics, mass transfer and chemical reactions, a well-defined experiment with a high spatial and temporal resolution is necessary. For this purpose, in this study, a single Taylor bubble is fixed through a countercurrent flow in a glass capillary, allowing systematic and detailed investigations of fluid dynamics and concentration fields in the bubble wake ideally unveiling their influences on yield and selectivity ⁷.

Taylor bubbles are large, elongated gas bubbles surrounded by a liquid film in small channels. The bubble diameter is slightly smaller than the diameter D of the capillary and the bubble is self-centering while staying elongated. The rising velocity is not determined by the bubble volume but depends on the ratio of buoyancy and surface tension, which can be described by the Eötvös number

()

where ρ_L and ρ_G are the densities of the liquid and gaseous phase, g is the gravitational constant and σ the surface tension. Depending on the dominating force, two different regimes can be distinguished. At high surface tensions or low capillary diameters yielding a critical Eötvös number of Eo_crit < 4, an external force moves the Taylor bubble. If the buoyancy dominates, the bubble rises autonomously and induces a flow field. The rising velocity v_B is set by the inner diameter of the capillary and varies the contact time of the different phases ^8-10. Furthermore, the inner capillary diameter influences the fluid dynamical time scales in the wake of the bubble. The Reynolds number gives a classification of fluid dynamical conditions and the mixing in the bubble wake

()

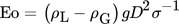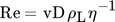where v is the characteristic velocity. Within this work, the characteristic velocity is set equal to the averaged velocity over the cross section v_c that is needed to fix the bubble in the countercurrent flow ¹¹, ¹².

Aim of this work is to investigate the influence of the mixing in the wake of the bubble on the selectivity regarding a main product P in a competitive consecutive gas liquid reaction. For this purpose, an integral but spatially and temporally resolved and a local definition of the selectivity are introduced and discussed ¹¹.

2 Material and Methods

2.1 Experimental Setup

The chemical system applied in this study is the oxidation of iron(II) chloride-tetrahydrate, FeCl₂·4H₂O (Sigma Aldrich; CAS: 13478-10-9; >99 %) and tetraethylammonium iodide, (C₂H₅)₄N(I) (Sigma Aldrich; CAS: 68-05-3; 98 %) using nitric oxide, NO (Westfalen AG, purity 2.0 = 99 vol %) in a methanol solution (ChemSolute, HPLC, gradient grade ≥ 99.9 %). This model reaction follows a consecutive competitive reaction scheme, producing in a first step an intermediate halogenido-mononitrosyliron compound (MNIC) at a reaction rate of k₁ (MNIC) = 5.0 · 10⁵ s⁻¹ (20 °C) and a dinitrosyliron compound (DNIC) at a reaction rate of k₂ = 0.04 s⁻¹ (20 °C) within the second reaction step ¹³. As both compounds exhibit a strong light absorption at different wavelengths of the visible light spectrum (MNIC: 470 nm, DNIC: 700 nm), the reaction is traceable by means of UV/VIS spectroscopy. The reactive system is based on the work by In-Iam et al. ¹⁴ and has been firstly introduced in ¹⁵.

As shown in Fig. 1, the experimental setup consists of a vertical glass capillary (L = 300 mm) that is connected to a reservoir. Valve 1 regulates the volume flow in the capillary necessary to fix the nitrogen monoxide bubble in the field of view of a high-speed camera (Phantom VEO640L, lens: Zeiss 2/50M ZF2.0 Makro Planar). The bubble is injected through a septum below the capillary by using a gastight syringe (Hamilton Gastight1001, 1 mL) and a hypodermic needle (Braun Sterican disposable cannula, 0.40 × 20 mm). To obtain different fluid dynamic conditions two different capillaries are used with diameters of D = 4.0 mm and D = 5.0 mm. The imaging UV/VIS spectroscopy has a field of view of (4 × 60) mm² and respectively (5 × 60) mm². Tab. 1 shows the characteristic fluid dynamic quantities, such as rise velocities and corresponding Reynolds number. The capillary is surrounded with a borosilicate glass duct filled with 97 wt % dimethyl sulfoxide (DMSO) (Roth; CAS: 67-68-5; >99.5 % purity) and deionized water to adjust the refractive index (n = 1.473 at 298 ± 1 K). The reservoir is connected to a flask filled with the reaction solution. The experiment is hermetically sealed and rinsed with argon (Westfalen AG, purity 5.0 ≥ 99.999 vol % purity) for 30 min before measurement to get an oxygen-free atmosphere. A volume of V_Res = 250 mL methanol is treated with argon for t = 10 min to remove other gases (degassing). The weight of 0.497 ± 0.001 g iron(II)-chloride and 2.572 ± 0.001 g iodided salt are added for a reaction solution (MNIC and DNIC are produced) with a starting concentration of c_Res(FeCl₂) = 10 mM. The reaction solution is again treated with argon during the entire measurement and held at a constant temperature of T = 288 K ± 1 K.

Table 1. Characteristic fluid dynamic quantities.

Diameter D [mm]	4	5
Mean countercurrent velocity vc [mm s−1]	6.83 ± 0.16	31.02 ± 1.45
Countercurrent flow rate QL [mm3s−1]	85.83 ± 2.01	609.08 ± 28.47
Eötvös-number Eo [–]	5.48	8.56
Reynolds-number Re [–]	36	207
Wake structure	laminar	turbulent vortices

To start the measurements, the reaction solution is brought into the capillary with a second gastight syringe (Hamilton Gastight1025, 25 mL) and a nitrogen monoxide bubble with a starting volume of V_b = 200 µL is injected. A 4 M NaOH solution scrubs the NO in advance to remove spurious NO₂ from the NO gas flux. The high-speed camera records the decreasing bubble size and the reactions using a LED panel as a back light. Two different LEDs with wavelength peaks of λ₁ = 470 ± 5 nm (LED 1: Würth Elektronik, WL-TMRC THT LED) and λ₂ = 700 ± 10 nm (LED 2: Panasonic, LN21RPX) that are near to the absorption maximum of the reaction products are installed. The LEDs are triggered with 90 Hz each to get a high temporal resolution so that an overall imaging frequency of 180 Hz results. Fig. 1 shows the resulting gray value images exemplary.

2.2 Determination of Product Concentrations

In order to calculate the concentration fields and therefore the selectivity in the wake of the bubble the imaging UV/VIS spectroscopy introduced by Kexel et al. ¹⁵ is applied. For a better understanding and completeness, the method will be shortly recapitulated. The analyzing procedure is based on Beer-Lamberts law

()

Since the products MNIC and DNIC have an absorption in both wavelength ranges of the LED illumination, the observed absorbance for each wavelength is calculated according to

()

()

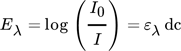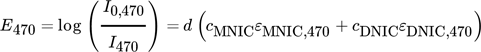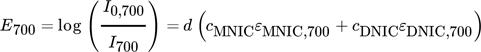E_λ describes the measured extinction, I₀ is the initial light intensity without absorbance caused by any reactant, I represents the light intensity due to absorbance, ε is the extinction coefficient, d describes the layer thickness of the liquid phase and c is the concentration. The extinction coefficients are experimentally determined for each wavelength and reaction product, directly within the Taylor bubble setup using the fiber optical UV/VIS spectroscopy probe. Based on the visual information it is assumed that the majority of the chemical reaction takes place at the center axis of the capillary, thus, the layer thickness d is assumed to be equal to the capillary diameter. If the resulting deviation between the assumed layer thickness d and the capillary is integrated over the capillary cross section and the value is divided by the number of pixels, a mean error of about 2 % is obtained. Nonetheless, this simplification tends to underestimate the concentrations close to the capillary boundaries. The deviations are, however, not significant for the determination of the selectivity, since the ratio of the concentrations is considered here. The initial light intensity I₀ is determined for each wavelength by averaging ten grayscale images of the educt solution, recorded before the NO bubble is injected. By rearranging Eqs. 6 and 7 the desired concentration fields in the wake of the bubble can be calculated pixel-wise for every pair of images (Fig. 2).

Due to spatial and temporal fluctuations within the initial light intensity I₀ the lower sensitivity limit of the concentration regarding the first product MNIC is about c_MNIC = 0.125 mmol L⁻¹ and about c_DNIC = 0.05 mmol L⁻¹ for the by-product DNIC. Therefore, concentration changes below those limits cannot be determined ¹⁵. The evaluation of the wake structures is performed on the basis of the characteristic Eötvös- and Reynolds numbers according to Kastens et al. ¹⁶. From the visualized results (videos V.1 and V.2 in the Supporting Information) one can clearly observe a more laminar flow without vortex structures in the D = 4 mm capillary and a more turbulent vortex structure in the D = 5 mm capillary. The vortex structures described in the work of Bugg et al. ¹⁷ could not be observed in the laminar flow case, which is probably due to the different media and their deviating viscosity.

The concentration fields show that both reaction steps are taking place. As the first reaction follows quiet fast kinetics, it is very likely that a majority of the first reaction step forming the MNIC takes place in the boundary layer. However, as the second product DNIC is detectable within the bubble wake ¹⁵, there must be unreacted NO dissolved in the liquid phase. Concluding from the observations it can be assumed that the first reaction follows an intermediate Hatta number (Ha = 0.02–2) calculated by Eq. 8 already simplified for first order reactions

()

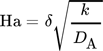with the reaction taking place in the interface and the bulk phase respectively ¹⁸. Though these assumptions need to be proven in further experimental work.

3 Results

To investigate the influence of mixing on the integral selectivity, two different mixing patterns are generated by using two different capillary sizes causing different bubble rising velocities, Reynolds numbers and thus wake mixing. For our analysis, the integral selectivity of the Product S_P is defined as the ratio of the amount of substance produced and the amount of educts converted considering the stoichiometric parameters ν_i and ν_P, yielding Eq. 9

()

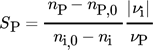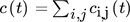Typically, the integral selectivity is determined by measuring the concentration differences of educts at the inlet and outlet and the amount of product at the outlet of the process step. In the present case, the integral selectivity is derived from the measured concentration fields in the Taylor bubble experiment. The total amount of the produced products MNIC and DNIC are summed up over a time interval t_obs = 4.2 s (750 images), which corresponds to the length of the experiment, for each pixel (i, j) within a fixed control volume, marked red in Fig. 2. Each pixel (i, j) represents a cubic volume element. The heights of the control volumes (h_cv,4mm = 0.067 mm and h_cv,5mm = 0.346 mm) are determined by the mean velocities v_c within the D = 4 mm and 5 mm capillary and the recording frequency (f = 180 Hz), i.e., h = v_c/f. In this way, a complete volume exchange can be assumed in between each concentration measurement. The concentration changes for each time step t_i of both reaction products can be described by the balance Eqs. 10 and 11

()

()

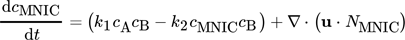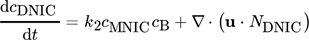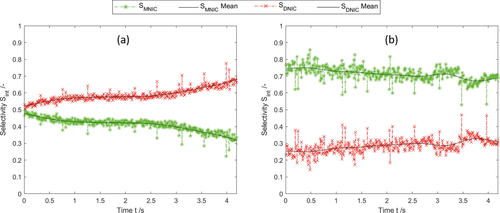
The first terms on the right-hand side are the amount of product produced and consumed in the control volume and the second term represent the substance fluxes going in and out of the volume. Since only the velocity component in the vertical direction is considered for the evaluation, the remaining components are thus negligible and the analysis results in a one-dimensional approach. By solving the balance equation for both products MNIC and DNIC from the concentration fields, the integral selectivity S_int,i at each time step t_i can be calculated applying Eq. 9. As the exact amount of converted educts cannot be determined at the outlet by means of UV/VIS spectroscopy (no relevant absorption), the total amount of educts converted is assumed as the sum of the amount of both products, MNIC and DNIC, 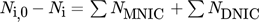since no further reaction step is possible. The temporal progression of the integral selectivity S_int,i for the time period from t₀ = 0 s to t_obs = 4.2 s is displayed in Fig. 3. Summing the substance amounts of N_MNIC and N_DNIC within the observed time t_obs yields the selectivity S_MNIC and S_DNIC for the entire process (Tab. 2) by applying Eq. 9.

In addition to the integral selectivity S_int,i at each time step and the selectivity S_MNIC and S_DNIC a temporally and spatially resolved integral selectivity within the bubble wake can be obtained from the concentration data. Therefore, the definition of the integral selectivity in Eq. 9 is applied to the measured concentration data pixel wise. The equation is solved for each pixel (i, j) within the field of view yielding a value for the selectivity of both products MNIC and DNIC

()

()

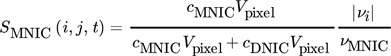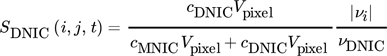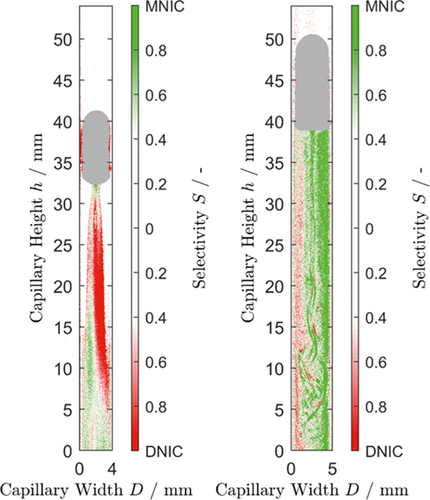
where it is assumed that 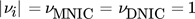. In order to evaluate whether the intermediate MNIC or the second product DNIC is the dominating species, the calculated temporally and spatially resolved selectivity for both products are merged into one comparing plot. As the selectivity cannot exceed values greater than 1, each pixel where S_MNIC ≥ 0.5 is marked with a green color map otherwise, when S_DNIC > 0.5 it is marked with a red one. The resulting Fig. 4 shows the data for one time step (t_i = 1.5 s), the corresponding videos V.3 and V.4 for all time steps can be found in the Supporting Information. Due to the lack of sensitivity at low concentrations, the error made at the calculations of the selectivity is about ± 0.213 for the intermediate MNIC and about ± 0.2561 for the by-product DNIC.

Like the integral selectivity and the process selectivity, the two graphics in Fig. 4 show the trend of an improved spatio-temporally resolved integral selectivity S_MNIC(i, j, t) for the intermediate MNIC at the D = 5 mm capillary, indicated by the large green areas in the plot. When looking at the plotted data in the D = 4 mm capillary (a), it becomes evident that there is already a high selectivity S_DNIC(i, j, t) regarding the second product DNIC in immediate vicinity behind the bubble, which is getting even higher with growing distance to the bubble. The shift towards the second reaction product DNIC in the wake of the bubble can be explained by the bad mixing occurring in the well-ordered wake flow and the availability of many MNIC molecules for each free NO molecule ¹⁵. However, the influence of the mixing does not account for the increased amount of DNIC in the direct vicinity of the bubble. Here, an influence of the residence time of the liquid phase in the thin liquid film around the Taylor bubble can likely explain this observation. Due to the lower liquid flow velocity of just v_c = 6.83 ± 0.16 mm s⁻¹ at the D = 4 mm capillary, the liquid phase remains much longer in close contact to the bubble and both reaction steps have more time to take place. This can be reflected by the first order Damköhler number, which is describing the ratio of the convective and reactive time scales following Eq. 14

()

The first reaction step forming the intermediate MNIC takes place rather instantaneously. The second reaction step for the formation of DNIC is taking longer due to the slower reaction kinetics and therefore benefits more from the longer contact time at high NO concentrations closer to the bubble. Nevertheless, the mixing conditions behind the bubble have a decisive influence on the selectivity, as can be seen in Fig. 4b, where its relative importance increases, when the contact time at the bubble is reduced due to faster flow velocities. Here, an exact measurement of the concentration boundary layer was not feasible. The influence of the liquid film and the residence time at the interface of bubbles has been addressed by Rüttinger et al. ¹⁹ and in case of Taylor bubbles in viscous media at laminar flow conditions has been addressed in Bugg et al. ¹⁷ and Meyer at al. ²⁰.

4 Discussion and Summary

The total values and the temporal trend of the overall integral selectivity determined in this work (Fig. 3 and Tab. 2) reveal that increasing the Reynolds number and thus intensifying mixing in the bubble wake favors a higher amount of the intermediate product MNIC while also yielding a significantly higher selectivity. By looking at the temporally and spatially resolved integral selectivity data (Fig. 4), those findings are even underlined. However, to fully understand the influence of the fluid dynamic conditions on the selectivity in competitive consecutive reactions, an approach applying a local selectivity, which is known from numeric studies conducted, e.g., by Khinast et al. ²¹ or more recently by Falcone et al. ²², is desirable. The local selectivity of a competitive consecutive reaction is defined by the reaction rates r₁ = k₁c_Ac_B and r₂ = k₂c_MNICc_B of the two products yielding the expression for the selectivity of the intermediate product according to

()

while the subtraction of the second reaction rate r₂ results from the consumption of the intermediate for the production of the unwanted second reaction product ¹⁶. It should be noted that there are several reasonable definitions of S_loc ¹⁷, ¹⁹. Compared to the numerically determined local selectivity by Khinast et al., the experimentally determined results are seemingly contradictory, which is particularly due to the different boundary conditions. Khinast et al. considered a freely rising bubble, which is not affected by wall effects and uses a definition of the local selectivity, which does not take into account the consumption of the intermediate product behind the gas bubble ²¹

()

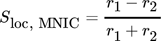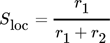The deviation of the data show that an adjustment of the numeric approaches to the experimentally considered case is necessary. However, it becomes also clearer that a direct comparison between numerically determined local selectivity and experimentally determined selectivity data is challenging and illustrates a clear knowledge gap, which needs to be closed in the future, by improved numerical approaches or experiments that are more sophisticated. Within numeric approaches all the initial parameters like mass flux, fluid dynamic conditions, concentrations of all reactants and reaction rates are exactly known or defined. This allows to describe all occurring dependencies mathematically and to solve them subsequently for each computational cell (schematically shown in Fig. 5). Thus, the local selectivity describes only the selectivity changes due to the reaction but neglects the convective mass flux. This is in contrast to the integral selectivity, which is evaluating the total amount of a product and cannot distinguish the local changes.

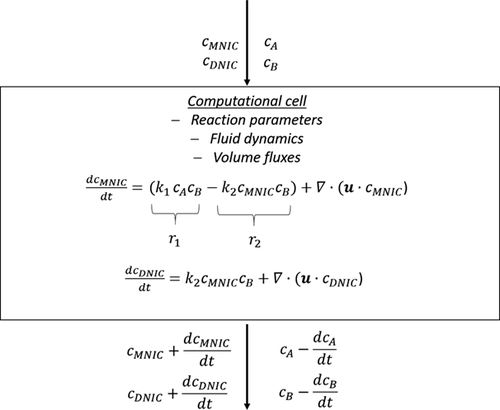
A local consideration of selectivity using experimental data would thus be desirable, not only for a better comparison to numeric approaches, but also for a deeper understanding of the influence of the local flow phenomena. However, measuring the required terms experimentally is very demanding. In order to determine the local selectivity in the wake of the bubble within future experimental studies, the substance flux due to inflow from different cells must be known in addition to the concentration fields, e.g., by superimposing 3D time-resolved flow field measurements by measurements techniques such as tomographic PIV. In addition, the measuring principle of imaging UV/VIS spectroscopy needs to be improved in sensitivity, as very small concentration changes cannot be evaluated yet, which is indispensable to visualize the small concentration changes occurring within a single cell or pixel in time. Since the experimental determination of local selectivity is to date unfeasible in absorption imaging, we suggest that numeric studies could in turn additionally determine spatio-temporally resolved integral selectivity for comparison.

By applying a newly developed UV/VIS imaging method we visualize the formation of several reaction products simultaneously at high temporal and spatial resolution. Based on the concentration fields in the wake of a fixed NO bubble the integral selectivity describing the complete reaction after different process times t_i is calculated. With the aid of a spatio-temporally resolved integral selectivity we observe the influence of mixing on a chemical competitive consecutive reaction.

Supporting Information

Supporting Information for this article can be found under DOI: 10.1002/cite.202000241. Movies: V.1: Concentration field behind the D = 4 mm capillary. V.2: Concentration field behind the D = 5 mm capillary. V.3: Temporally and spatially resolved selectivity in the bubble wake of the D = 4 mm capillary. V.4: Temporally and spatially resolved selectivity in the bubble wake of the D = 5 mm capillary. For further information please contact the corresponding author.

Symbols

Greek letters

Sub- and Superscripts

Abbreviations