SMART-Reactors: Tailoring Gas Holdup Distribution by Additively Manufactured Lattice Structures
Abstract
In chemical process engineering, fast gas-liquid reactions often suffer from an inefficient distribution of gas and therefore mixing and mass transfer performance. This study deals with the possibility of influencing the local gas holdup and bubble size distribution in a gas-liquid process using additively manufactured lattice structures (AMLS). The used measuring technique to study bubble size, velocity, and the local gas holdup is a photo-optical needle probe. By using AMLS, a significant radial homogenization of the local gas holdup and the mean bubble size is achieved. Furthermore, it can be demonstrated that the bubble size can be tailored by the geometry of the inserted structure. It is illustrated that the mean bubble velocities are lowered within the lattice resulting in a higher residence time of the dispersed phase with an impact on the mass transfer performance within the AMLS.
1 Introduction
The design of industrial gas-liquid reactors is still challenging because the gas holdup and the bubble sizes, in particular, the specific surface areas available for mass transfer are difficult to control. For this purpose, both microscopic and macroscopic models as well as empirical correlations are required, which provide information on process efficiency concerning mass transport, reaction conditions, mixing, as well as on the material system itself and its specific properties 1, 2. In particular, the question of the bubble size distribution prevailing in the reactor and thus the specific surface area of the phases involved poses a problem in many cases due to the opaque steel industrial apparatuses, with too dense bubbly flows for current measurement techniques.
Structured packings and internals have already proven their remedial potential in the past. Hölemann et al. 3 showed positive effects on fluid dynamics and mass transport of various structured packings in bubble columns manufactured by conventional production methods for different gas-liquid systems. Thus, process intensification by improved mass transfer could be shown especially for rapidly coalescent systems with low dispersion of the gas phase by using structured packings 3. In 2012, Shah et al. investigated different packings (packed, trayed or empty bubble columns) concerning the gas holdup, axial dispersion, and mass transfer and stated that packed and trayed bubble columns improve gas holdup and mass transfer compared to an empty bubble column while significantly reducing axial dispersion 4. Lesniak also extensively studied the structuring of bubble columns and investigated phase distribution, hydrodynamics, and mass transport performance for various structured packings. By installing structured packings, it was possible to show more defined flow conditions with potentially more targeted reaction control and at the same time a lower risk in designing bubble columns on a pilot plant scale 5, 6.
Additive manufacturing is an innovative and rapidly growing technology and in spite of its versatility, it is barely applied in the chemical process industry. The review article by Parra-Cabrera et al. provides a good overview of the different methods and application possibilities 7. Up to now, the printing size and/or printing times of commercial equipment have always been a deficit, so that it has received little attention for the industrial application in larger plants. However, this circumstance is changing visibly and while the built volume is getting bigger and the production times are getting shorter, there are now printing methods that can produce models 25–100 times faster than most common 3D printers 8. The technology is also becoming more and more important for industrial standards in process engineering.
Here, additive manufacturing of lattice structures are used to tailor properties in gas-liquid flows, such as the bubble size distribution, the specific surface area, and thus the mass transport and reactor performance. This work is intended to contribute to the newly gained possibilities by means of additive manufacturing and to illustrate the potential in process engineering in the manner of designing SMART (sustainable, multipurpose, artificial intelligent, resilient, transferable) reactors.
2 State-of-the-Art: Influence of Additively Manufactured Structured Internals on the Gas-Liquid Distribution
In process engineering, the new capabilities of additive manufacturing have been already investigated in former studies. Especially, periodic open-cell structures (POCS), which are a subtype class of additively manufactured lattice structures (AMLS) that in contrast can also be designed aperiodically or fractally, are the object of various research 9-18. In the following, a literature survey will be given, stating also the advantage of the used geometry design in this work considering past research in this field.
In 2014, Klumpp et al. investigated ideal cubic structures with regard to the influence of porosity and cell orientation on pressure loss 12. Cubic cells were viewed in different orientations considering the flow direction, namely 15-0, 30-0, 45-0 and 30-30, whereby the 30-30 orientation is most similar to the unit cell type and orientation used in this work (cf. Fig. 1e and f, Tab. 1). The numbers demonstrate the tilting of a homogeneous upright standing cubic periodic open-cell structure by an angle α in Z-Y or β in Z-X direction. The Z-axis arrow (blue) is always stating the flow direction through the unit cell in Fig. 1.
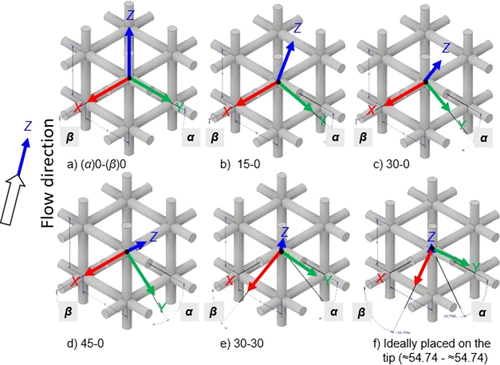
Looking at the top cross-sectional views, the most homogeneous distribution can be assumed for the choice of the cubic structure, which is ideally placed on the tip, radially in X and Y direction, as this is symmetrical in both directions parallel to the flow direction influencing the flow in the same way. Since the other structures (15-0, 30-0, and 45-0) have an unequal ratio of lengths to widths of the free surfaces along the flow direction (different flow resistance), an inhomogeneous distribution in X and Y direction is expected. With the 30-30, the non-ideal setting (30° compared to ≈ 54.74°) also causes a tendency of the bubbles to move by trend in one radial direction, as there is no symmetry here either. Compared to the 30-30, the cubic on the tip has less flow resistance due to the larger area available for unhindered bubble ascent in flow direction (Tab. 1).
In 2016, Inayat et al. derived a pressure loss correlation including web geometry and tortuosity for open cell foams, which are characterized by a particularly high specific surface area for, e.g., heterogeneously catalyzed applications 11. Open cell foams do have a very high surface-to-volume ratio compared to periodic open-cell structures, but due to their dense packing, they cannot be adapted for gas-liquid reactions because bubbles are being entrapped or blocking the flow through the foam and consequently the pressure drop varies a lot. Also in 2016, Lämmermann et al. investigated the use of periodic open-cell structures of more complex unit cells (Kelvin cell, Diamond cell, and a DiaKel, i.e., a hybrid cell of these two) and their influence on the gas-liquid distribution using a liquid collector in a trickle-bed reactor 14. Later, these structures were characterized with respect to their liquid holdup and the two-phase pressure drop and thus their potential for process intensification 13. Similar to Busse et al. 2016, Bianchi et al. 2018 looked at the advantages of using POCS for increased and intensified heat transfer in fixed-bed catalytic reactors 10, 16. The structures made of highly heat-conductive materials can be used to enhance process safety and reaction control for exo- or endothermic reactions.
Baltussen et al. 2017 simulated the cutting of bubbles with a single wire and validated their in-house used code experimentally. They combined the volume-of-fluid and the immersed-boundary method, thus showing a good agreement with the experimentally obtained bubble sizes after cutting as well as regarding bubble shapes, trajectory, and bubble rise velocities 19. In 2019, Hecht et al. 17 also demonstrated that POCS can increase the integral gas holdup and thus make a significant contribution to reactor performance. In the work, it was also found that the radial distribution of the gas phase is improved, which was tested by means of a wire mesh sensor (WMS) for various industrially relevant gas-liquid systems. The investigated cell geometry was a 45° inclined cubic POCS, which was also used by Klumpp et al. 12 (cf. Fig. 1 and Tab. 1). Furthermore, Hecht conducted mass transport investigations, tracer experiments for residence time measurements, and liquid mixing studies regarding the usage of POCS in bubble column reactors. The pilot-scale bubble column under investigation had a diameter D of 150 mm and a height H of 1450 mm, resulting in an H/D ratio of 8.67 17, 20.
Llamas et al. investigated POCS for the application of Lagrangian analysis techniques to gain new insights into reactor dynamics. This could be a valuable tool to identify and characterize areas with different mixing performance and to further optimize the geometry design 21. Most recently, Do et al. presented an approach of so-called interpenetrated periodic open cellular structures (interPOCS) as a geometrically flexible system enabling in operando adjustment of fluid flow characteristics. InterPOCS consist of two interwoven POCS that can be adjusted to reach, e.g., a specific pressure drop level in operando by changing the distance of the two interconnected structures affecting the flow resistance 18. This approach opens a new dimension of designing 3D-printed structures for the use in chemical engineering.
From this literature survey it gets clear that many studies have already been conducted, showing that the gas holdup can be increased and radially homogenized by structuring. For the orientation of the structure employed in this work (cubic on the tip), an even better distribution is expected, symmetrically in all spatial directions. In addition, the bubble sizes and bubble velocities are examined to determine the extent to which a mean bubble diameter can be adjusted by the structures (H/D ratio) after a certain residence time. This knowledge will be adapted to other AMLS for further reactor performance optimization.
3 Experimental Procedures
3.1 Experimental Setup
The measured and discussed data include the local gas holdup distribution, the Sauter mean diameter, and the mean bubble velocities. In Fig. 2, one can see the schematic experimental setup and the order of the investigated structures as well as a photo of the operated bubble column. In the first experiments, conventional cubic POCS are investigated according to the orientation ideally placed on the tip (cf. Fig. 1 and Tab. 1).
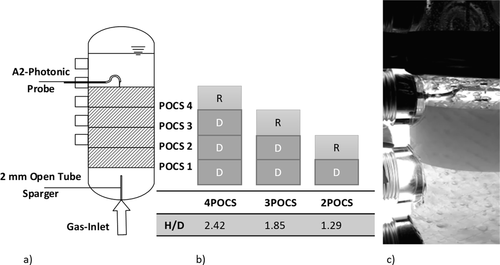
The local gas holdup is measured radially at nine positions (Fig. 3). In empty bubble columns, a random set of measured chord length values differs considerably from the real bubble size distribution 22, 23. Therefore, in this work, a so-called “rectifier structure” (Fig. 3) is used to assure that each bubble is touched by the needle probe in the center of a cell. As a result, the chord sizes determined converge more to the real bubble sizes and the use of the rectifier structure serves to increase the accuracy of the measurement. For the determination of bubble size distributions from chord size distributions there are different means based on stochastic assumptions. Since the use of the structures lead to chord length distributions closer to the actual bubble sizes compared to an empty bubble column, only chord lengths distributions are evaluated in this work.
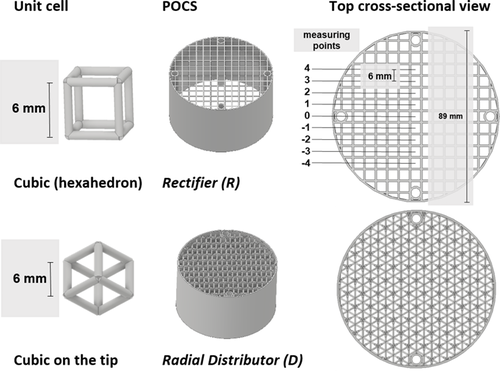
The local gas holdup ε, the mean bubble velocity ub, the chord sizes lc, and the mean bubble diameter (Sauter mean diameter d32) are determined. Tab. 2 presents the experimental conditions of the needle-probe measurments. The investigated POCS with a height of 50 mm each were placed 1 cm above the open tube sparger with a nozzle diameter of 2 mm, which was centrally positioned. An air volume flow rate of 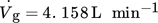 was used, which corresponds to a superficial gas velocity of ug = 0.011 m s−1. The Reynolds number was calculated with respect to two characteristic lengths, i.e., the reactor diameter of D = 89 mm (ReRD) and the strut thickness of 1 mm (ReSD). The tests were performed in deionized water under ambient conditions (p = 1013 hPa, T = 20 ± 1 °C). The structures are stereolithographically manufactured out of clear standard resin (V4) by means of a Form 2 3D printer of the company Formlabs Inc.
was used, which corresponds to a superficial gas velocity of ug = 0.011 m s−1. The Reynolds number was calculated with respect to two characteristic lengths, i.e., the reactor diameter of D = 89 mm (ReRD) and the strut thickness of 1 mm (ReSD). The tests were performed in deionized water under ambient conditions (p = 1013 hPa, T = 20 ± 1 °C). The structures are stereolithographically manufactured out of clear standard resin (V4) by means of a Form 2 3D printer of the company Formlabs Inc.
|
Temperature T [°C] |
Pressure p [hPa] |
Gas flow rate |
Superficial gas velocity ug [m s−1] |
ReRD [–] |
ReSD [–] |
|---|---|---|---|---|---|
|
20 ± 1 |
1013 |
4.16 |
0.011 |
986.9 |
66.5 |
3.2 Measuring Technique
Local measurements of bubbles were conducted with an optical needle probe (A2 Photonics Sensors B-POP). This probe (Fig. 4a) enables the local characterization of a multiphase flow utilizing an optical signal that is collected through a fine glass tip. The signal is caused by the different refractive index of the gaseous and liquid phase. For this purpose, the A2 Photonics Sensors' BPOP optical system is based on a class 1 laser with a maximum power of 3 mW and a wavelength of 830 nm. Whenever the sensing tip penetrates a bubble (see Fig. 4b), the refractive index of the collected signal changes and the bubble is thereby registered (cf. Figs. 4c and d). This measuring principle allows high-accuracy measurements of a) local concentration (void fraction), b) bubble velocity, and c) inclusion chord.
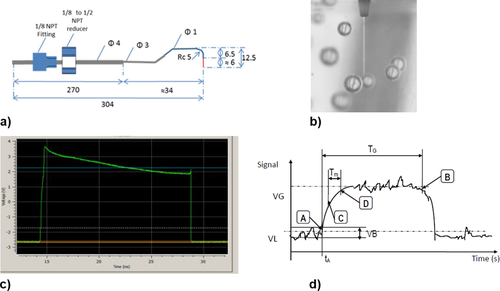
The needle probe is installed through a port on the side of the bubble column and can be adjusted to different radial positions (see Fig. 5). In this work, the radial distance from the center of the column x = 0 mm is representing the position 0 at the center of the column and a distance of y = 44.5 mm representing the column wall (inner diameter of the column is 89 mm). The sensing tip of the probe was always positioned at h = 1 cm above a cell center of the POCS.

Preliminary measurements show in accordance with literature 25 that a total number of 2500 bubbles per measurement is a sufficient number of bubbles in order to yield constant results regarding gas holdups and mean bubble diameters. These result values oscillate at some positions, especially in the region near the wall, where the frequency at which a bubble is detected is lower than near the center, and thus the time needed for the gas holdup to reach a constant value is accordingly longer. In general, the maximum acquisition time that was needed at positions near the column wall was 200 s, whereas in most cases a constant value for the gas holdup was already reached after about 20 s.
The optical signal acquired from the sensing part of the probe is converted inside an optoelectronic module into an analog and digital electrical signal that can be further processed by the signal processing software. This software, in turn, calculates three characteristic time values, from which all other results are derived. These values are schematically illustrated in Fig. 4d depicting a typical bubble signal and comprise a) the arrival time of a bubble (tA), i.e., the time interval between the start of the data acquisition and the bubble detection, b) the residence time of the sensing tip inside a bubble (TG), and c) the rising time of the signal (TM) indicating the transition from the liquid to the gaseous phase. These three measurement values along with the calibration parameters of the probe are utilized in order to calculate the gas concentration (void fraction) as derived by the time ratio inside the gaseous and the liquid phase, the velocity of each bubble when pierced by the tip of the probe as derived by the rising time TM, and the chord of each bubble that was run through by the probe as derived by the residence time TG inside the bubble. All these data can be displayed in various ways, like in chord histograms and velocity histograms, including all “well-shaped” bubbles that surpassed the probe detection threshold of 500 μm (cf. Figs. 4c and d), as well as all “interpolated” bubble recordings, i.e., partial signals or glitches, whose signal was lower than the detection threshold and thus did not form a plateau.
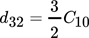 (1)
(1)The above empirical correlation was validated by measuring the mean diameter of single bubbles with the use of a high-speed camera and comparing the acquired proportionality factor between the chord lengths determined by the needle probe and the actual diameter of the respective bubbles. The result was slightly higher than 3/2, i.e., 1.6. Nevertheless, the fact that all measurements were conducted with the same probe under the same conditions allows for the assumption of a systematic error and for the usage of the results to illustrate the expected homogenization of the bubble size over the column radius with the use of AMLS.
4 Results and Discussion
4.1 Local Gas Holdup in Structured Packings
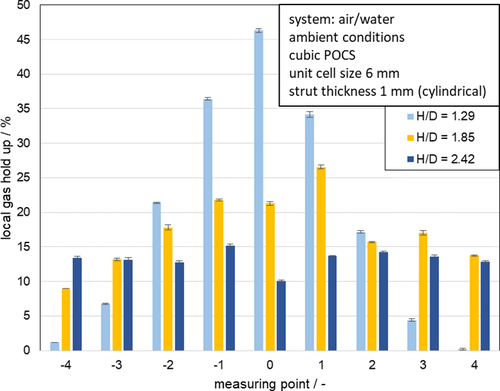
Fig. 6 compares the local gas holdup for three different arrangements of POCS. For the local gas holdup distribution, a successive homogenization with the addition of structures can be seen: After H/D = 1.29 (two structures) the profile shows the well-known maximum gas holdup at the center (measuring point 0), after H/D = 1.85 (three structures) this profile is already significantly flatter and wider. After H/D = 2.42 (four structures) the holdup is almost constant over the cross section. It should be noted that the application using a bar chart is necessary for the measured values, since the local gas holdup between the respective cell centers, above the webs, cannot be measured. This is due to the fact that the needle probe can hardly detect any signal of a bubble directly behind the webs, as the probability of the presence of bubbles is very low compared to the center of the cell where the measurement was performed.
4.2 Local Bubble Sizes in Structured Packings
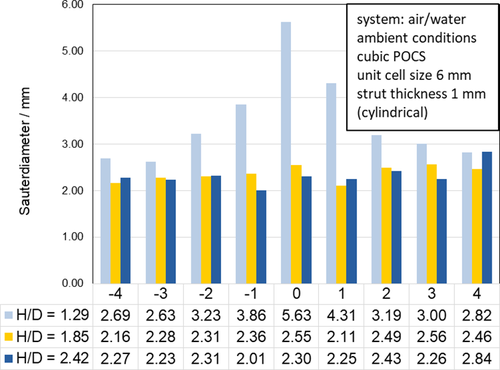
The evaluation of the Sauter mean diameters, according to Fig. 7, also shows a uniformity with the increasing packing height, namely, with the ratio of the height of the structuring to the reactor diameter (H/D). The Sauter mean diameter decreases from 5.63 mm after H/D = 1.29 (two structures) in the reactor center to 2.32 ± 0.21 after H/D = 2.42 (four structures) on average. In addition, this value is relatively constant for H/D = 2.42 (four structures) over the entire reactor diameter. Only the measured value for H/D = 2.42 and measuring point 4 deviates slightly from the trend at 2.84. This is probably an outlier in which the spontaneous coalescence could have led to a significantly increased chord length and thus to a local increase in Sauter mean diameter at the measurement point.
Basically, the Sauter mean diameter is strongly dependent on the size of the largest measured bubbles 25. However, this can be significantly reduced when using POCS in which continuous bubble breakup occurs. This generally leads to a higher reliability of the Sauter mean diameter itself as bubble column design criterion, as larger bubbles are almost impossible. It is also remarkable that the Sauter mean diameter is homogenized over the reactor diameter after only three structures according to H/D = 1.85. The Sauter mean diameter in an empty tube without structured internals is definitely bigger than 10 mm under the same conditions.
It can be stated that the bubble size is tailored by the cell size. For deeper insights, the measured chord length distributions for the different structures are illustrated in Fig. 8.
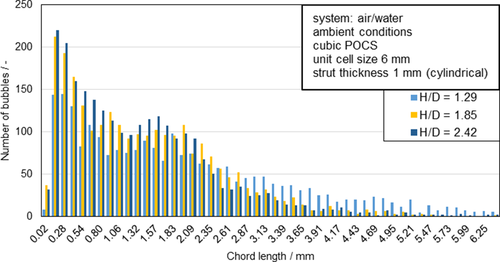
It can be seen how the values, which are bimodally distributed for the respective series of measurements, move with the height or the number of structures, respectively, further to the left towards the smaller bubbles and thus, contrary to coalescence, tend to a defined narrower bubble size distribution with an increased specific surface area. This is expected to lead to an increase in mass transport in the course of an absorption, desorption or a chemical reaction 17, 26.
4.3 Bubble Velocities in Structured Packings
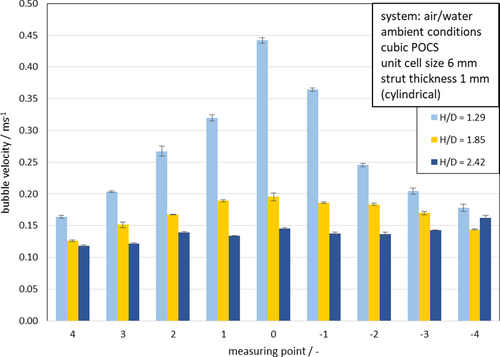
A look at Fig. 9 and Tab. 3 indicates that the average speed decreases over the height of structures. Exemplarily for position 0 (center of the column), the deceleration from the original absolute bubble velocity of 0.44 m s−1 after H/D = 1.29 (two structures) over 0.20 m s−1 at H/D = 1.85 (three structures) and finally to 0.15 m s−1 after H/D = 2.42 (four structures) leads to a simultaneous increase in the mean residence time of the bubbles and thus to a longer contact time for mass transfer within the system. This is reasonable because, as a result of bubble breaking, the bubbles are smaller, have a lower volume and therefore a lower buoyancy force and rising velocity.
The mean residence times are calculated on the basis of the measured bubble velocities assuming a straight rising path and no occurring acceleration after exiting the structure. The mean residence time increases from 0.26 s to 1.47 s. In fact, this deceleration and enhanced residence time will also affect the reaction performance, since the contact time of the participating phases plays an important role in chemical and biochemical reactions. Depending on the system, this circumstance can be used to adjust the reactor performance. For fast reactions, a structuring with lower resistance for the ascending bubbles might be suitable to lower the residence time whereas for hardly soluble gases (like hydrogen) a stronger deceleration of the bubbles with longer residence time might be useful. This will be investigated for more sophisticated nonperiodic structure geometries and with regard to the influence on mass transport and the effects on a selective chemical reaction in future research.
|
H/D |
Mean velocities ub [ms−1] |
Mean residence time τ [s] |
|---|---|---|
|
2.42 |
0.15 |
1.47 |
|
1.85 |
0.20 |
0.83 |
|
1.29 |
0.44 |
0.26 |
5 Conclusion
It has been demonstrated that additively manufactured lattice structures (AMLS) have a great potential for tailoring the two-phase flow in gas-liquid reactors. The investigated periodic open cell structures (POCS) as simplest class of AMLS enabled a significant radial homogenization of the local gas holdup as well as the mean bubble size in the form of a narrower distribution and a uniform Sauter mean diameter over the reactor radius. This homogenization already occurred after H/D = 1.85. The bubble size distribution can be tailored by the use of POCS, which makes further investigations necessary to transfer these findings to AMLS.
Furthermore, the determined mean bubble velocities showed a deceleration of the bubbles within the structures and thus a higher residence time. This constitutes another partial effect of the enhanced mass transfer caused by POCS and can be utilized for further reactor performance optimization with AMLS as a new degree of freedom in designing reactors. The use of rectifier structures improves the measurement accuracy of needle probe measurement technology and might be of interest for other measurements with this kind of probes.
This is the first out of three studies by the authors dealing with this topic. In the next step, the influence of AMLS on mass transport will be examined, especially due to the bubble dynamics and velocity effects. In the third step, the results will be transferred to parallel consecutive chemical reactions.
Acknowledgements
The authors gratefully acknowledge the financial support which was given by the Federal State of Hamburg under grant number LFF-FV 43. The project is associated to the joint research project “New reactor technologies for chemical and biochemical synthesis processes”. Open access funding enabled and organized by Projekt DEAL.
The authors have declared no conflict of interest.
Symbols used
-
- a [m−1]
-
specific surface area
-
- C10 [mm]
-
cumulative averaged chord length
-
- d32 [mm]
-
Sauter mean diameter
-
- lc [mm]
-
chord length
-
- Re [–]
-
Reynolds number
-
- ub [m s−1]
-
mean bubble velocity
-
- ug [m s−1]
-
superficial gas velocity
-
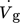 [L min−1]
[L min−1] -
gas flow rate
Greek letters
-
- α [°]
-
angle
-
- β [°]
-
angle
-
- ε [–]
-
local gas holdup
-
- τ [s]
-
mean residence time
Sub- and superscripts
-
- RD
-
reactor diameter
-
- SD
-
strut diameter
Abbrevations
-
- AMLS
-
additively manufactured lattice structures
-
- D
-
radial distributor
-
- POCS
-
periodic open-cell structures
-
- R
-
rectifier
-
- WMS
-
wire mesh sensor








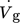 [L min−1]
[L min−1]

