Brain‐X
Volume 3, Issue 1 e70014
RESEARCH ARTICLE
Open Access

VMD-FBCCA classification method for SSVEP brain–computer interfaces

Ping Tan, 

Corresponding Author

Ping Tan

School of Intelligent Engineering and Intelligent Manufacturing, Hunan University of Technology and Business, Changsha, Hunan, China

Xiangjiang Laboratory, Changsha, Hunan, China

Correspondence

Ping Tan, No. 569 YueLu Avenue, Changsha 410205, China.

Email: [email protected]

Contribution: Funding acquisition, ​Investigation, Methodology, Project administration, Supervision, Writing - review & editing

Search for more papers by this author
Fengsheng Wang, 

Fengsheng Wang

School of Intelligent Engineering and Intelligent Manufacturing, Hunan University of Technology and Business, Changsha, Hunan, China

Contribution: Writing - original draft

Search for more papers by this author
Kaijun Zhou, 

Kaijun Zhou

School of Intelligent Engineering and Intelligent Manufacturing, Hunan University of Technology and Business, Changsha, Hunan, China

Xiangjiang Laboratory, Changsha, Hunan, China

Contribution: Resources, Validation

Search for more papers by this author
Yi Shen, 

Yi Shen

School of Intelligent Engineering and Intelligent Manufacturing, Hunan University of Technology and Business, Changsha, Hunan, China

Contribution: Visualization

Search for more papers by this author
First published: 18 January 2025
https://doi.org/10.1002/brx2.70014

Abstract

A steady-state visually evoked potential (SSVEP) is a brain response to specific frequencies of visual stimuli, including their harmonic frequencies. However, this signal is susceptible to interference from spontaneous α $\alpha $ and β $\beta $ rhythms in electroencephalography (EEG) signals because they overlap from 8 to 40 Hz. This can reduce the recognition accuracy of SSVEP brain–computer interfaces (BCIs). To address this problem, a variational mode decomposition–based filter bank canonical correlation analysis (VMD-FBCCA) algorithm is proposed, which integrates the adaptive characteristics of VMD and the training-free nature of the FBCCA algorithm. First, the EEG signal of each channel is transformed into intrinsic mode functions (IMFs) by the VMD algorithm, which extracts frequency components of the SSVEP from each IMF. Next, a particle swarm algorithm is employed to optimize the weights of the IMFs and reconstruct the EEG signals. This reconstruction selectively enhances the IMFs in the target SSVEP frequency band while suppressing interference from other bands. Finally, the reconstructed EEG is classified using FBCCA to decode the SSVEP-BCI signal. To evaluate its effectiveness, the proposed algorithm is tested on datasets from the BCI Competition. The results demonstrate that VMD-FBCCA outperforms FBCCA, showing improvements in both the average recognition accuracy ( 6.04 % ) $(6.04\%)$ and information transmission rate (8.91 bits/min). Moreover, the best recognition accuracy achieved for individual subjects is enhanced by 29.17 % $29.17\%$ .

Key points

What is already known about this topic?

  • Steady-state visual evoked potential (SSVEP) is a popular brain–computer interface (BCI) paradigm with a high information transfer rate and minimal training requirements. There are many recognition algorithms for SSVEPs. However, the intrinsic mode function (IMF) components obtained by variational mode decomposition include interference from spontaneous electroencephalography (EEG) signals, which affects the recognition accuracy of SSVEP BCIs.

What does this study add?

  • To distinguish spontaneous EEG signals and target SSVEP rhythm signals, this study optimizes the weights of IMFs using a particle swarm optimization (PSO) algorithm. This improves the recognition accuracy of SSVEP signals. PSO is employed to find the best IMF weights to ensure that those of SSVEP target rhythms are larger, mitigating the problem of SSVEP and spontaneous EEG signals overlapping within the frequency coverage range.

Abbreviations

  • BCI
  • brain-computer interface
  • EEG
  • electroencephalography
  • SSVEP
  • steady-state visual evoked potential
  • VMD-FBCCA
  • variational mode decomposition-based filter bank canonical correlation analysis

    • 1 INTRODUCTION

    Brain–computer interfaces (BCIs) are revolutionary human–computer interaction systems that enable users to control external devices directly with their thoughts, bypassing the traditional pathways of peripheral nerves and muscles. BCIs work by recording brain activity, such as electroencephalography (EEG) signals, and then translating them into commands that can be sent to an external device.1 BCIs have been widely used in military applications, medical rehabilitation, and assisting older and disabled people, and a great deal of research progress has been made.

    Steady-state visual evoked potential (SSVEP) is a popular BCI paradigm with a high information transfer rate and minimal training requirements.2-4 It refers to the brain's response to visual stimuli that flicker at a constant frequency. The response EEG signal is consistent with the stimulation frequency or its harmonics.5 An SSVEP-based BCI needs to recognize the target frequency to decode the user's intention. There are many SSVEP recognition algorithms, including multivariate synchronization index (MSI) and canonical correlation analysis (CCA) approaches. CCA-based algorithms are widely used because no training is required.

    CCA6 finds the maximum correlation between EEG and reference signals to identify the SSVEP target frequency. It can achieve a higher recognition accuracy than MSI algorithms and other classifiers for power spectral density (PSD) features. However, CCA is only effective at extracting information from the base frequency, not from the harmonic frequencies. To solve this problem, a filter bank CCA (FBCCA) algorithm7 has been proposed, which combines fundamental and harmonic frequency components to improve the identification accuracy of EEG signals. This algorithm decomposes the EEG signal into multiple sub-bands through a filter bank; it then uses CCA to find the maximum correlation between each sub-band component of the EEG and reference signals to identify the SSVEP target frequency. FBCCA improves recognition accuracy and is more effective than earlier CCA algorithms.

    In addition, CCA-based algorithms need signal preprocessing to remove noise artifacts in EEG signals, which may be caused by eye or muscle motion, before feature extraction. However, standard preprocessing algorithms cannot effectively remove the noise in EEG signals. Ge8 proposed a decoding algorithm based on FBCCA and beamforming, which enables high-precision algorithms without training for the research of SSVEP-BCI systems.9-11 The performance of these improved algorithms is better than that of CCA, but only traditional filters are used in noise artifact removal, proving insufficiently effective.

    The recognition accuracy of FBCCA not only depends on the reference signal but also on clear EEG data without noise artifacts. Therefore, the question of how to efficiently remove noise artifacts in EEG signals is important.12 Empirical mode decomposition (EMD) is a highly efficient denoising algorithm,13 that decomposes complicated data into a small number of intrinsic mode functions (IMFs) for noise elimination. These IMFs provide time-dependent instantaneous frequencies, aiding in precise structure identification. A major drawback of EMD is mode mixing, which causes aliasing in the time–frequency distribution. The ensemble EMD algorithm14, 15 addresses mode mixing in EMD by leveraging its scale separation ability. Adding finite noise ensures proper segregation of different-scale signals into distinct IMFs.

    However, EMD algorithms are limited to the analysis of empirical modes and have difficulty in determining endpoint effects and stopping conditions. A fully non-recursive variational mode decomposition (VMD) has been proposed16 that incorporates the signal into a variational model and leverages an optimized constrained version to achieve decomposition, resulting in more stationary sub-signals.17, 18 Because the secondary penalty factor in VMD can improve convergence and remove noise in decomposed modes, this algorithm can be used to remove visual and ECG artifacts19, 20 in EEG signals. However, the IMF components obtained by VMD have frequency overlap between the SSVEP and the spontaneous EEG signal, which affects the recognition accuracy of SSVEP BCIs.21-23

    To distinguish between spontaneous EEG signals and target SSVEP rhythm signals, the main idea of this paper is to optimize the weights of IMFs using a PSO algorithm.24 Increasing the weights of the target SSVEP rhythm signal and reducing the weights of the spontaneous EEG signal ensures that the target SSVEP rhythm is strengthened in the reconstructed EEG to improve the recognition accuracy of SSVEP BCIs.

    The main contribution can be summarized as follows:

    1. Variational mode decomposition–based filter bank canonical correlation analysis (VMD-FBCCA) is proposed, an algorithm that combines the adaptability of VMD and the training-free advantages of FBCCA algorithms. It reconstructs the modes containing the main signals to remove noise artifacts from EEG signals effectively. By extracting useful information from harmonic frequency components, this method improves the recognition accuracy of SSVEP signals.

    2. PSO is employed to find the best IMF weights to ensure that the weights of SSVEP target rhythms are larger and those of spontaneous EEG activity are smaller. It mitigates the problem of overlap between SSVEPs and spontaneous EEG signals within the frequency coverage range.

    The remainder of the paper is structured as follows: Section 2 reviews related work on CCA and FBCCA. Section 3 introduces VMD, PSO, and the VMD-FBCCA algorithm. Section 4 presents the experimental results, and Section 5 discusses them. Section 6 concludes the paper.

    2 RELATED WORKS

    2.1 Canonical correlation analysis

    CCA is a statistical technique that aims to investigate correlations between two sets of data variables or vectors, enabling the inference of their similarity. It is employed in SSVEP detection to identify the components of the EEG response signal and the reference signal with the highest degree of similarity. For two multi-dimensional variables X $\boldsymbol{X}$ and R $\boldsymbol{R}$ , CCA finds the pair of linear transformations W x ${\boldsymbol{W}}_{\boldsymbol{x}}$ , W r ${\boldsymbol{W}}_{\boldsymbol{r}}$ that maximize the correlations between x = X T W x $\boldsymbol{x}={\boldsymbol{X}}^{\boldsymbol{T}}{\boldsymbol{W}}_{\boldsymbol{x}}$ and r = R T W r $\boldsymbol{r}={\boldsymbol{R}}^{\boldsymbol{T}}{\boldsymbol{W}}_{\boldsymbol{r}}$ . This can be expressed as the following optimization problem:
    max W x , W r ρ ( x , r ) = E W x T X R T W r E W x T X X T W x E W r T R R T W r $\underset{{\boldsymbol{W}}_{\boldsymbol{x}},{\boldsymbol{W}}_{\boldsymbol{r}}}{\max }\rho (\boldsymbol{x},\boldsymbol{r})=\frac{E\left[{\boldsymbol{W}}_{\boldsymbol{x}}^{T}{\boldsymbol{X}\boldsymbol{R}}^{T}{\boldsymbol{W}}_{\boldsymbol{r}}\right]}{\sqrt{E\left[{\boldsymbol{W}}_{\boldsymbol{x}}^{T}{\boldsymbol{X}\boldsymbol{X}}^{T}{\boldsymbol{W}}_{\boldsymbol{x}}\right]E\left[{\boldsymbol{W}}_{\boldsymbol{r}}^{T}{\boldsymbol{R}\boldsymbol{R}}^{T}{\boldsymbol{W}}_{\boldsymbol{r}}\right]}}$ (1)
    where ρ $\rho $ represents the maximum correlation coefficient. In the context of SSVEP detection, X $\boldsymbol{X}$ represents multi-channel SSVEP signals and R $\boldsymbol{R}$ denotes reference signals. For unsupervised detection of SSVEP frequencies, sinusoidal signals serve as the reference signal, designated as R f ${\boldsymbol{R}}_{f}$ :
    R f = sin ( 2 π f t ) cos ( 2 π f t ) ⋮ sin ( 2 π n h f t ) cos ( 2 π n h f t ) , t = 1 Q , 2 Q , … , T Q ${\boldsymbol{R}}_{f}=\left[\begin{array}{@{}c@{}}\hfill \sin (2\pi ft)\hfill \\ \hfill \cos (2\pi ft)\hfill \\ \hfill {\vdots}\hfill \\ \hfill \sin (2\pi nhft)\hfill \\ \hfill \cos (2\pi nhft)\hfill \end{array}\right],t=\frac{1}{Q},\frac{2}{Q},\text{\ldots },\frac{T}{Q}$ (2)
    where f $f$ denotes the base frequency, n $n$ the number of harmonics, Q $Q$ the sampling rate, and T $T$ the number of sample points.

    To identify the target frequency of the SSVEP, CCA determines the canonical correlation between the SSVEP and reference signals across various stimulation frequencies. The frequency corresponding to the highest correlation is designated as the target frequency.

    2.2 Filter bank CCA

    FBCCA is an improved CCA algorithm designed to extract the useful information embedded within the base and harmonic frequency components. The algorithm first decomposes the SSVEP signal into N $N$ sub-components of different frequency bands with filter banks, and then CCA is performed on these sub-components to obtain the correlation coefficient between each sub-component and the reference signal. The correlation vector ρ r ${\rho }_{r}$ of the r $r$ -th reference signal is defined as follows:
    ρ r = ρ r 1 ρ r 2 ⋮ ρ r N = ρ X B 1 T W X X B 1 R f r , R T W R X B 1 R f r ρ X B 2 T W X X B 2 R f r , R T W R X B 2 R f r ⋮ ρ X B N T W X X B N R f r , R T W R X B N R f r ${\boldsymbol{\rho }}_{r}=\left[\begin{array}{@{}c@{}}\hfill {\rho }_{r}^{1}\hfill \\ \hfill {\rho }_{r}^{2}\hfill \\ \hfill {\vdots}\hfill \\ \hfill {\rho }_{r}^{N}\hfill \end{array}\right]=\left[\begin{array}{@{}c@{}}\hfill \rho \left({\boldsymbol{X}}_{B1}^{T}{\boldsymbol{W}}_{\boldsymbol{X}}\right.\left({\boldsymbol{X}}_{B1}{\boldsymbol{R}}_{{f}_{r}}\right),{\boldsymbol{R}}^{T}{\boldsymbol{W}}_{\boldsymbol{R}}\left({\boldsymbol{X}}_{B1}{\boldsymbol{R}}_{{f}_{r}}\right)\hfill \\ \hfill \rho \left({\boldsymbol{X}}_{B2}^{T}{\boldsymbol{W}}_{\boldsymbol{X}}\right.\left({\boldsymbol{X}}_{B2}{\boldsymbol{R}}_{{f}_{r}}\right),{\boldsymbol{R}}^{T}{\boldsymbol{W}}_{\boldsymbol{R}}\left({\boldsymbol{X}}_{B2}{\boldsymbol{R}}_{{f}_{r}}\right)\hfill \\ \hfill {\vdots}\hfill \\ \hfill \rho \left({\boldsymbol{X}}_{BN}^{T}{\boldsymbol{W}}_{\boldsymbol{X}}\right.\left({\boldsymbol{X}}_{BN}{\boldsymbol{R}}_{{f}_{r}}\right),{\boldsymbol{R}}^{T}{\boldsymbol{W}}_{\boldsymbol{R}}\left({\boldsymbol{X}}_{BN}{\boldsymbol{R}}_{{f}_{r}}\right)\hfill \end{array}\right]$ (3)
    where the N $N$ -th sub-band components of X $\boldsymbol{X}$ are represented by X B N ${\boldsymbol{X}}_{BN}$ , and f r ${f}_{r}$ denotes the frequency of the r $r$ -th reference signal R $R$ . As a feature for target identification, a weighted sum of squares of the correlation values is computed, encompassing all sub-band components:
    ρ ∼ r = ∑ n = 1 N w ( n ) . ρ r n 2 ${\tilde{\rho }}_{r}=\sum\limits _{n=1}^{N}w(n).{\left({\rho }_{r}^{n}\right)}^{2}$ (4)
    where n $n$ serves as the index for the sub-band. The weights assigned to the sub-band components are specified as follows:
    w ( n ) = n − a + b , n ∈ { 1 , 2 , … , N } $w(n)={n}^{-a}+b,n\in \left\{1,2,\text{\ldots },N\right\}$ (5)
    where the constants a $a$ and b $b$ are chosen to optimize the classification performance. The frequency of the reference signal exhibiting the highest ρ ∼ r ${\tilde{\rho }}_{r}$ value is deemed as the target frequency of the SSVEP. It can be observed that the sub-bands of the filter bank cover multiple harmonic frequency bands with a high cutoff frequency at the upper-bound frequency of the SSVEP components.7 The FBCCA is presented in Algorithm 1.

    Algorithm 1. FBCCA

    • Input: X $X$ , N $N$ , a $a$ , b $b$ , R $R$

    • Output: target

    • 1: Design N $N$ band-pass filters.

    • 2: for n = 1:N  do

    • 3:   X B n ← B a n d F i l t e r n ( X ) ${\boldsymbol{X}}_{\boldsymbol{B}\boldsymbol{n}}\hspace*{.5em}{\leftarrow}\hspace*{.5em}\boldsymbol{B}\boldsymbol{a}\boldsymbol{n}\boldsymbol{d}\boldsymbol{F}\boldsymbol{i}\boldsymbol{l}\boldsymbol{t}\boldsymbol{e}{\boldsymbol{r}}_{\boldsymbol{n}}(\boldsymbol{X})$

    • 4:   Compute ρ r n ${\rho }_{r}^{n}$ by Equation (3)

    • 5: end for

    • 6: Compute ρ ∼ r ${\tilde{\rho }}_{r}$ by Equations (4) and (5)

    • 7: target ← ${\leftarrow}$ Index ( max ( ρ ∼ r ) ) $(\max ({\tilde{\rho }}_{r}))$

    3 VMD-BASED FBCCA

    3.1 Variational mode decomposition

    VMD is an adaptive and non-recursive signal processing algorithm that can identify the optimal center frequency and bandwidth for each mode during the decomposition process. It effectively separates the IMF components in the EEG signal decomposition and finally obtains the optimal solution of the variational problem. The decomposed IMF component set u k ( t ) ${u}_{k}(t)$ is defined as:
    u k ( t ) = A k ( t ) cos φ k ( t ) ${u}_{k}(t)={A}_{k}(t)\cos \left({\varphi }_{k}(t)\right)$ (6)
    where A k ( t ) ${A}_{k}(t)$ represents the amplitude function and φ k ( t ) ${\varphi }_{k}(t)$ denotes the phase function of u k ( t ) ${u}_{k}(t)$ .
    Under the constraint that the sum of all decomposition modes is equal to the original signal f $f$ , VMD minimizes the sum of the estimated bandwidths of all decomposition modes. This constrained variational formula for VMD is
    min u k , w k ∑ k = 1 K ∂ t δ ( t ) + j π t ∗ u k ( t ) e − j ω k t 2 2 s . t . ∑ k = 1 K u k = f \begin{align*}\hfill & \underset{\left\{{u}_{k}\right\},\left\{{w}_{k}\right\}}{\min }\left\{\sum\limits _{k=1}^{K}{\left\Vert {\partial }_{t}\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast {u}_{k}(t)\right]{e}^{-j{\omega }_{k}t}\right\Vert }_{2}^{2}\right\}\hfill \\ \hfill & \quad s.t.\quad \sum\limits _{k=1}^{K}{u}_{k}=f\hfill \end{align*} (7)
    where u k ${u}_{k}$ and ω k ${\omega }_{k}$ are the k $k$ -th ( k = 1 , 2 , … , K ) $(k=1,2,\text{\ldots },K)$ mode and center frequency of the VMD, respectively, ∗ $\ast $ is the convolutional operator, ∂ $\partial $ is the partial differential operator, and δ ( t ) $\delta (t)$ is the Dirac distribution.
    By employing the augmented Lagrange function, the constrained variational problem is converted into an unconstrained one, enabling the computation of the optimal solution. The formula is
    L u k , ω k , λ = α ∑ k = 1 K ∂ t δ ( t ) + j π t ∗ u k ( t ) e − j ω k t 2 2 + f ( t ) − ∑ k = 1 K u k ( t ) 2 2 + λ ( t ) , f ( t ) − ∑ k = 1 K u k ( t ) \begin{align*}\hfill L\left(\left\{{u}_{k}\right\},\left\{{\omega }_{k}\right\},\lambda \right)& =\alpha \sum\limits _{k=1}^{K}{\left\Vert {\partial }_{t}\left[\left(\delta (t)+\frac{j}{\pi t}\right)\ast {u}_{k}(t)\right]{e}^{-j{\omega }_{k}t}\right\Vert }_{2}^{2}\hfill \\ \hfill & +{\left\Vert f(t)-\mathop{\sum}\limits_{k=1}^{K}{u}_{k}(t)\right\Vert }_{2}^{2}\hfill \\ \hfill & +\left\langle \lambda (t),f(t)-\mathop{\sum}\limits_{k=1}^{K}{u}_{k}(t)\right\rangle \hfill \end{align*} (8)
    where λ $\lambda $ is a Lagrange multiplier, α $\alpha $ is a quadratic penalty factor, and the alternating direction method of multipliers is used to continuously update the center frequency and bandwidth. Here, the role of Lagrange multipliers is to strengthen constraints and accurately reconstruct EEG signals. The effect of the quadratic penalty is to improve convergence, which can remove the noise in the decomposed IMF.
    The frequency-domain components should be updated using the following formula:
    u ˆ k n + 1 ( ω ) = f ˆ ( ω ) − ∑ i ≠ k u ˆ i ( ω ) + λ ˆ ( ω ) / 2 1 + 2 α ω − ω k ${\widehat{u}}_{k}^{n+1}(\omega )=\frac{\widehat{f}(\omega )-{\sum }_{i\ne k}{\widehat{u}}_{i}(\omega )+\widehat{\lambda }(\omega )/2}{1+2\alpha \left(\omega -{\omega }_{k}\right)}$ (9)
    where u ˆ k n + 1 ( ω ) ${\widehat{u}}_{k}^{n+1}(\omega )$ , f ˆ ( ω ) $\widehat{f}(\omega )$ and λ ˆ ( ω ) $\widehat{\lambda }(\omega )$ are the Fourier transforms of u k n + 1 ω k ${u}_{k}^{n+1}\left({\omega }_{k}\right)$ , f ω k $f\left({\omega }_{k}\right)$ and λ ω k $\lambda \left({\omega }_{k}\right)$ , respectively, the center frequency of each component is estimated at the power spectrum's center of gravity, and ω k n + 1 ${\omega }_{k}^{n+1}$ is updated using Equation (10). The detailed steps of the VMD are presented in Algorithm 2. The VMD Python package25 is available at https://github.com/vrcarva/vmdpy.
    ω ˆ k n + 1 = ∫ 0 ∞ ω | u ˆ k n + 1 ( ω ) | 2 d ω ∫ 0 ∞ | u ˆ k n + 1 ( ω ) | 2 d ω ${\widehat{\omega }}_{k}^{n+1}=\frac{\int \nolimits_{0}^{\infty }\omega \vert {\widehat{u}}_{k}^{n+1}(\omega ){\vert }^{2}d\omega }{\int \nolimits_{0}^{\infty }\vert {\widehat{u}}_{k}^{n+1}(\omega ){\vert }^{2}d\omega }$ (10)

    Algorithm 2. VMD

    • Input: f , K , α , ε $f,K,\alpha ,\varepsilon $ ;

    • Output: u k , u ˆ k , ω k $\left\{{u}_{k}\right\},\left\{{\widehat{u}}_{k}\right\},\left\{{\omega }_{k}\right\}$

    • 1: Initialize u ˆ k 1 ${\widehat{u}}_{k}^{1}$ , ω ˆ k 1 ${\widehat{\omega }}_{k}^{1}$ , λ ˆ 1 ${\widehat{\lambda }}^{1}$ ;

    • 2: for n = 1:N do

    • 3:   Update u ˆ k n + 1 ${\widehat{u}}_{k}^{n+1}$ , ω ˆ k n + 1 ${\widehat{\omega }}_{k}^{n+1}$ according to Equations (9) and (10);

    • 4:   Update λ ˆ n + 1 ( ω ) ${\widehat{\lambda }}^{n+1}(\omega )$ according to λ ˆ n + 1 ( ω ) = λ ˆ n ( ω ) + τ f ˆ ( ω ) − ∑ k u ˆ k n + 1 ( ω ) ${\widehat{\lambda }}^{n+1}(\omega )={\widehat{\lambda }}^{n}(\omega )+\tau \left(\widehat{f}(\omega )-{\sum }_{k}{\widehat{u}}_{k}^{n+1}(\omega )\right)$ ;

    • 5:   δ = ∑ k ‖ u ˆ k n + 1 − u ˆ k n ‖ 2 2 ‖ u ˆ k n ‖ 2 2 $\delta =\frac{{\sum }_{k}\Vert {\widehat{u}}_{k}^{n+1}-{\widehat{u}}_{k}^{n}{\Vert }_{2}^{2}}{\Vert {\widehat{u}}_{k}^{n}{\Vert }_{2}^{2}}$

    • 6:  if δ > ε $\delta > \varepsilon $ then

    • 7:   Continue;

    • 8:  else

    • 9:          Break;

    • 10:end if

    • 11: end for

    • 12: Output u k n + 1 , u ˆ k n + 1 , ω k n + 1 $\left\{{u}_{k}^{n+1}\right\},\left\{{\widehat{u}}_{k}^{n+1}\right\},\left\{{\omega }_{k}^{n+1}\right\}$ .

    As can be seen from the above discussion, the VMD algorithm involves solving a constrained variational problem, using mathematical tools such as quadratic penalty terms, Lagrange multipliers, and augmented Lagrange functions, to find the optimal IMFs that satisfy the bandwidth and reconstruction constraints. It updates the IMFs and their center frequencies iteratively until a convergence criterion is met, such as a small change ε $\varepsilon $ in the IMFs or center frequencies between iterations. In the presence of overlapping frequencies, the key advantage of the VMD algorithm is its variational principle, which allows the algorithm to consider the local characteristics of the signal during the decomposition process. By optimizing the bandwidth and center frequency of each IMF, the VMD algorithm can adaptively separate signal components corresponding to specific SSVEP frequencies.

    Because the IMF components decomposed by the VMD are still only components of the original SSVEP signal, and there is still a problem of frequency coverage overlap between it and spontaneous EEG signals, such as α $\alpha $ waves (8–12 Hz), it needs to optimize the IMF weights to weaken the IMF components with interference bands. In this paper, the PSO algorithm is employed to complete the optimization process.

    3.2 Particle swarm optimization

    PSO is a random population algorithm inspired by the intelligent swarming behavior of birds.26, 27 It is straightforward to implement, requires little parameter adjustment, and can achieve rapid convergence.28

    For the position x → i t = x i , 1 t , x i , 2 t , … , x i , D t ${\overrightarrow{x}}_{i}^{t}=\left[{x}_{i,1}^{t},{x}_{i,2}^{t},\text{\ldots },{x}_{i,D}^{t}\right]$ and speed v → i t = v i , 1 t , v i , 2 t , … , v i , D t ( i ∈ { 1 , 2 , … , NP } ) ${\overrightarrow{v}}_{i}^{t}=\left[{v}_{i,1}^{t},{v}_{i,2}^{t},\text{\ldots },{v}_{i,D}^{t}\right]\ (i\in \left\{1,2,\text{\ldots },\mathit{NP}\right\})$ of the i $i$ -th particle at generation t $t$ in a D $D$ dimension search space, PSO considers the fitness value of each particle according to the fitness function f x → i t $f\left({\overrightarrow{x}}_{i}^{t}\right)$ and makes each particle gather to the individual optimal position p best ${p}_{\mathit{best}}$ and global optimal position g best ${g}_{\mathit{best}}$ of the particle with the best fitness value. After iteratively updating the particle position and speed, the fitness value is reduced as much as possible to find the optimal solution. The process by which the particle positions and velocities are updated in each iteration is as follows:
    x i , j t + 1 = x i , j t + v i , j t ${x}_{i,j}^{t+1}={x}_{i,j}^{t}+{v}_{i,j}^{t}$ (11)
    v i , j t + 1 = ω v i , j t + c 1 r 1 p best i , j t − x i , j t + c 2 r 2 g best j t − x i , j t ${v}_{i,j}^{t+1}=\omega {v}_{i,j}^{t}+{c}_{1}{r}_{1}\left({{p}_{\mathit{best}}}_{i,j}^{t}-{x}_{i,j}^{t}\right)+{c}_{2}{r}_{2}\left({{g}_{\mathit{best}}}_{j}^{t}-{x}_{i,j}^{t}\right)$ (12)
    where the inertia weight is denoted by ω $\omega $ , c 1 ${c}_{1}$ and c 2 ${c}_{2}$ represent two acceleration factors, and r 1 ${r}_{1}$ and r 2 ${r}_{2}$ are two random numbers drawn uniformly from the range [0, 1]. At each generation, the velocity v i , j t + 1 ${v}_{i,j}^{t+1}$ is constrained to the range − v max , v max $\left[-{v}_{\max },{v}_{\max }\right]$ .

    3.3 VMD-based FBCCA

    The framework of the VMD-FBCCA algorithm is illustrated in Figure 1. It has two core modules, VMD and FBCCA. The EEG signal is first decomposed by the VMD algorithm and then reconstructed with the optimal weight obtained by PSO. The FBCCA core module extracts features from the fundamental and harmonic frequencies in the reconstructed EEG signal, achieving classification of SSVEP signals; for more details, refer to Ref. [7].

    Details are in the caption following the image
    FIGURE 1
    Open in figure viewerPowerPoint

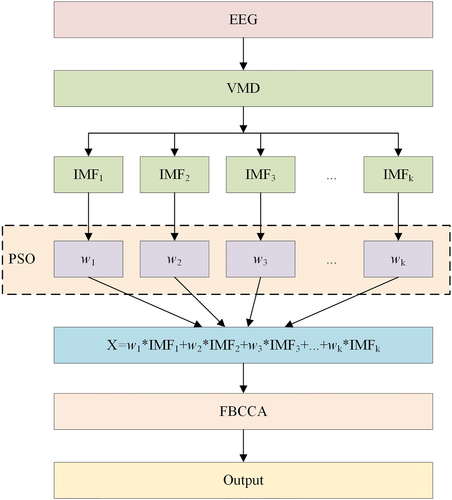
    Framework of VMD-FBCCA. VMD-FBCCA, variational mode decomposition–based filter bank canonical correlation analysis.

    The implementation of the algorithm can be divided into training and testing phases. The goal of the training phase is to find the optimal reconstructed weights, as described by Algorithm 3. There are two main steps. First, it is necessary to determine the parameters of the VMD algorithm: the level of decomposition K $K$ , the penalty factor α $\alpha $ , the fidelity coefficient ε $\varepsilon $ , and the stop condition s c ${s}_{c}$ . The algorithm decomposes the EEG into K $K$ IMFs, as described in Section 3.1:
    x i → I i 1 , I i 2 , … , I i K ${\boldsymbol{x}}_{\boldsymbol{i}}\to \left\{{\boldsymbol{I}}_{\boldsymbol{i}\boldsymbol{1}},{\boldsymbol{I}}_{\boldsymbol{i}\boldsymbol{2}},\text{\ldots },{\boldsymbol{I}}_{\boldsymbol{i}\boldsymbol{K}}\right\}$ (13)
    where x i ${\boldsymbol{x}}_{\boldsymbol{i}}$ is the i $i$ -th channel of EEG, and I i k ${\boldsymbol{I}}_{\boldsymbol{i}\boldsymbol{k}}$ is the k $k$ -th IMF component of x i ${\boldsymbol{x}}_{\boldsymbol{i}}$ .
    Second, the PSO algorithm is employed to adjust the reconstruction weights w $\boldsymbol{w}$ by evaluating the classification error rate e r ${e}_{r}$ . This is computed by FBCCA, for which an implementation is available at https://github.com/TBC-TJU/MetaBCI. The reconstructed EEG is calculated according to Equation (14).
    x ∼ m = w m , 1 I 1 + w m , 2 I 2 + ⋯ + w m , K I K . ${\tilde{\boldsymbol{x}}}_{m}={w}_{m,1}{\boldsymbol{I}}_{\mathbf{1}}+{w}_{m,2}{\boldsymbol{I}}_{\mathbf{2}}+{\cdots}+{w}_{m,K}{\boldsymbol{I}}_{\boldsymbol{K}}.$ (14)
    where w m , k ${w}_{m,k}$ is the k $k$ -th value of the weight corresponding to the m $m$ -th particle.

    Algorithm 3. Training phase of VMD-FBCCA

    • Input: x $\boldsymbol{x}$ , K $K$ , α $\alpha $ , ε $\varepsilon $ , s c ${s}_{c}$

    • Output: w gbest ${\boldsymbol{w}}_{\mathit{gbest}}$

    • 1: t = 0 $t=0$ , e g = e p = 1.0 ${e}_{g}={e}_{p}=1.0$ ;

    • 2: Initialize w 0 ${\boldsymbol{w}}^{0}$ , v 0 ${\boldsymbol{v}}^{0}$ ;

    • 3: Decompose EEG x $\boldsymbol{x}$ into K $\boldsymbol{K}$ IMFs by VMD as shown in 3.1:

    • 4:   V M D ( x , K , α , ε ) → I 1 , I 2 , … , I K $\boldsymbol{V}\boldsymbol{M}\boldsymbol{D}(\boldsymbol{x},\boldsymbol{K},\alpha ,\varepsilon )\to \left\{{\boldsymbol{I}}_{1},{\boldsymbol{I}}_{2},\text{\ldots },{\boldsymbol{I}}_{K}\right\}$ ;

    • 5: while the stopping criterion s c ${s}_{c}$ is not met  do

    • 6:  for m = 1:M do

    • 7:    x ∼ m = w m , 1 t I 1 + w m , 2 t I 2 + … + w m , K t I K ${\tilde{\boldsymbol{x}}}_{m}={w}_{m,1}^{t}{\boldsymbol{I}}_{1}+{w}_{m,2}^{t}{\boldsymbol{I}}_{2}+\text{\ldots }+{w}_{m,K}^{t}{\boldsymbol{I}}_{K}$ ;

    • 8:    L m ${\boldsymbol{L}}_{m}$  = FBCCA x ∼ m $\left({\tilde{\boldsymbol{x}}}_{m}\right)$ , as shown in algorithm 1;

    • 9:     Compute classification error rate e r ${e}_{r}$ ;

    • 10:   if e r < e p ${e}_{r}< {e}_{p}$ then

    • 11:     e p = e r ${e}_{p}={e}_{r}$ , w pbest t ← w m t ${\boldsymbol{w}}_{\mathit{pbest}}^{t}\hspace*{.5em}{\leftarrow}\hspace*{.5em}{\boldsymbol{w}}_{m}^{t}$ ;

    • 12:   end if

    • 13:   if e p < e g ${e}_{p}< {e}_{g}$  then

    • 14:     e g = e p ${e}_{g}={e}_{p}$ , w gbest t ← w pbest t ${\boldsymbol{w}}_{\mathit{gbest}}^{t}\hspace*{.5em}{\leftarrow}\hspace*{.5em}{\boldsymbol{w}}_{\mathit{pbest}}^{t}$ ;

    • 15:   end if

    • 16:  end for

    • 17:  for m = 1:M do

    • 18:    w m t + 1 = w m t + v m t ${\boldsymbol{w}}_{m}^{t+1}={\boldsymbol{w}}_{m}^{t}+{\boldsymbol{v}}_{m}^{t}$ ;

    • 19:    v m t + 1 = ω v m t + c 1 r 1 w pbest t − w m t + c 2 r 2 w gbest t − w m t ${\boldsymbol{v}}_{m}^{t+1}=\omega {\boldsymbol{v}}_{m}^{t}+{c}_{1}{r}_{1}\left({\boldsymbol{w}}_{\mathit{pbest}}^{t}-{\boldsymbol{w}}_{m}^{t}\right)+{c}_{2}{r}_{2}\left({\boldsymbol{w}}_{\mathit{gbest}}^{t}-{w}_{m}^{t}\right)$ ;

    • 20:  end for

    • 21:   w gbest = w gbest t ${\boldsymbol{w}}_{\mathit{gbest}}={\boldsymbol{w}}_{\mathit{gbest}}^{t}$ ;

    • 22:  t = t + 1

    • 23: end while

    During the testing phase, the following steps are performed:

    1. The VMD algorithm is used to decompose the EEG of each channel into IMFs of K $K$ different frequency bands.

    2. The EEG x ∼ g ${\tilde{\boldsymbol{x}}}_{g}$ is reconstructed with the best weight w g ${\boldsymbol{w}}_{g}$ obtained by PSO during the training phase. The weighted sum of IMF components is calculated according to Equation (14).

    3. Using FBCCA to classify the reconstruct x ∼ g ${\tilde{\boldsymbol{x}}}_{g}$ EEG signal.

    This VMD-FBCCA algorithm combines the adaptive VMD and training-free FBCCA algorithms. It reconstructs the modes containing the main signals to remove noise artifacts from EEG signals effectively and extracts the useful information embedded in the harmonic frequency components to improve the recognition accuracy of SSVEP signals. In addition, the PSO algorithm, which is easy to implement and converges rapidly, is used to optimize the weights of IMFs in different frequency bands to better distinguish SSVEPs from spontaneous EEG signals and improve the recognition accuracy of SSVEPs.

    4 EXPERIMENTS AND RESULTS

    4.1 Experimental datasets

    The experimental dataset is derived from the BCI Controlled Robot Contest held during the World Robot Contest in 2021.29 The paradigm of the dataset is SSVEP-based multi-target keyboard spelling, with 40 stimulation targets. The stimulation frequency is from 8 to 15.8 Hz, with an interval of 0.2 Hz, and the phase difference between adjacent frequencies is 0.5 π $\pi $ . This dataset was recorded from 12 healthy subjects using eight electrodes: POz, PO3, PO4, PO5, PO6, Oz, O1, and O2. For each subject, there are three training blocks and three test blocks, and each block has 40 trials. Because noise and artifacts influence signal recognition, the original EEGs were filtered through a 6–100 Hz bandpass filter and a 50 Hz notch filter to eliminate noise caused by equipment, alternating current, and ocular artifacts.

    4.2 Parameters setting

    The decomposition level K $K$ is an important parameter affecting the decomposition performance of VMD. If K $K$ is too small, this will lead to insufficient decomposition of EEG signals. If it is too large, the frequencies will overlap, and more computation time will be required. In either case, the reconstruction of EEG signals will be negatively affected. In this work, K $K$ was set to 5.

    For a constant decomposition level K $K$ , the bandwidth of a component yielded by the decomposition is inversely proportional to the penalty factor α $\alpha $ , If α $\alpha $ is too large, this will cause the reconstructed signal to lose some of the information from the original signal. If it is too small, spectral mixing and overlapping between adjacent modes will occur. In this paper, α = 240 $\alpha =240$ , the fidelity coefficient ε = 0.4 $\varepsilon =0.4$ , and the stop condition s c = 1 0 − 7 ${s}_{c}=1{0}^{-7}$ .

    Among the parameters of the PSO algorithm, the inertia weight ω $\omega $ plays a pivotal role in determining both the local and global search capabilities. A smaller value of ω $\omega $ enhances the local search ability while compromising the global search ability. The learning factors c 1 ${c}_{1}$ and c 2 ${c}_{2}$ regulate the movement step sizes of particles, guiding them toward their respective individual optimal positions and the global optimal position. Their settings will affect the particles' trajectories. In this paper, ω = 0.85 $\omega =0.85$ , c 1 = c 2 = 2 ${c}_{1}={c}_{2}=2$ . The limit condition is within the range of [−10, 10], with the number of particles set to 50 and the number of iterations to 100. The fitness function f ( x ) $f(x)$ is the error recognition rate:
    f ( x ) = 1 − A c c $f(x)=1-Acc$ (15)
    where A c c $Acc$ is the recognition accuracy.
    In addition to accuracy, the information transmission rate (ITR) serves as a crucial performance metric for assessing the transmission capabilities of a BCI. The calculation formula is
    I T R = 60 T log 2 I + P log 2 P + ( 1 − P ) log 2 1 − P I − 1 $ITR=\frac{60}{T}\left[{\log }_{2}I+P{\log }_{2}P+(1-P){\log }_{2}\frac{1-P}{I-1}\right]$ (16)
    where I $I$ represents the number of stimulation frequencies, P $P$ is the recognition accuracy, and T $T$ is the duration of the selected EEG signal (in the experiment, T = 2.5 s $T=2.5s$ ).

    4.3 IMF weight results after PSO optimization

    The PSO algorithm optimizes the weight parameters using the training data from each subject (228 trials) to minimize the value of the fitness function. Figure 2 shows iteration diagrams for the fitness value of the PSO-optimized weight of the 12 subjects.

    Details are in the caption following the image
    FIGURE 2
    Open in figure viewerPowerPoint

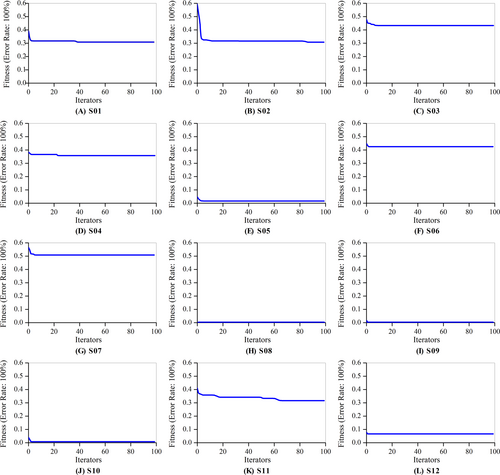
    Parameter optimization iteration diagrams for 12 subjects.

    It can be seen that the fitness value (error rate) in each of the 12 diagrams gradually decreases over the course of the iterations and converges to a stable value. Among them, S02, S03, and S11 show a clear decrease in error during the convergence process. The error reduction of S01, S04, S05, S06, S07, and S10 is relatively small, whereas in the remaining cases, S08, S09, and S12, the error decreases only marginally. Overall, this means that the PSO algorithm exhibits a fast convergence speed and achieves a degree of error reduction.

    When the SSVEP signal is decomposed into variational modes, the number of IMF components K $K$ needs to be defined in advance. For a given K $K$ value, it is necessary to randomly select the initial weight value within the limit condition range, and then the PSO algorithm determines the fitness value of each particle according to the fitness function and aggregates each particle to the individual optimal weight and global optimal weight of the particle with the best fitness value. The process is iterated under the finite cycle condition, updating the particle weight and speed, reducing the fitness value as much as possible, and finding the optimal solution.

    In this study, 60 (12 subjects × ${\times} $ 5 intrinsic modals) weights were optimized using the PSO algorithm. The optimized weights are shown in Figure 3; the darker the color, the greater the weight. It can be seen that all weights for S03 and S06 are >4.0, whereas all weights for S05, S07, S08, S09, S10, S11, and S12 are >0. Some weights for S01, S02, and S04 are positive and others negative. This illustrates the variability of SSVEP signals between different subjects.

    Details are in the caption following the image
    FIGURE 3
    Open in figure viewerPowerPoint

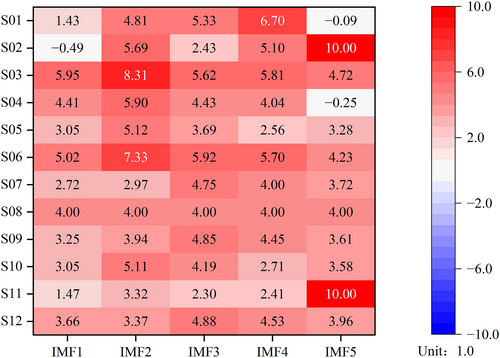
    Weights obtained after optimization for 12 subjects.

    Two points should be noted here. First, the negative weights, as seen with S02's IMF1 and S01's IMF5, imply that these IMFs have a negative impact on the results and need to be suppressed. This is analogous to the suppression of a 50 Hz power frequency interference with a notch filter. Second, some extreme values are obtained, such as 10.0 for S02's IMF5. Because the PSO optimization process relies on the fitness function to adjust the optimization direction, the adjusted parameters may not be physically meaningful. Thus, although increasing the IMF5 weights improved the SSVEP recognition performance, there may be differences in physical understanding. Therefore, we have limited the range of weights to within 10 and do not allow them to be increased further to prevent possible deterioration.

    Except for the extreme value, the weights for IMF1, IMF2, and IMF3 are relatively large, meaning that the features of IMFs at medium and low frequencies (4–30 Hz) are related to the high recognition accuracy. This also verifies the difference between SSVEP signals in different frequency bands.

    4.4 Comparison of VMD-FBCCA results with other methods

    This subsection compares the SSVEP recognition accuracy and ITR of the VMD-FBCCA, FBCCA, EMD-CCA, and ensemble empirical mode decomposition (EEMD)-CCA algorithms on the same dataset. In the experiment, the reference signal harmonic number of FBCCA was set to 5, and the weight parameters a $a$ and b $b$ were set to 1 and 0.96, respectively. The parameter decomposition mode number for EMD-CCA and EEMD-CCA was set to 5. Table 1 presents the recognition accuracy of the four algorithms across the 12 subjects, and in each row, the bold value is the best one among the results of four algorithms. Figure 4A shows the ITR results in a bar chart.

    TABLE 1. Accuracy of the four algorithms.
    Subjects FBCCA EMD-CCA EEMD-CCA VMD-FBCCA
    S01 49.17 55.83 61.25 69.17
    S02 40.00 41.67 45.74 69.17
    S03 55.83 55.83 57.45 56.67
    S04 63.33 63.33 63.33 64.17
    S05 94.17 94.17 94.17 98.33
    S06 53.33 53.33 54.53 57.50
    S07 42.50 43.33 45.50 49.17
    S08 100.00 100.00 100.00 100.00
    S09 99.17 99.17 99.17 100.00
    S10 97.50 98.33 98.87 99.17
    S11 58.33 61.23 63.33 68.33
    S12 91.67 91.67 92.32 93.33
    AVG 70.42 71.49 72.97 77.08
    STD 23.95 23.15 21.98 19.54
    • Abbreviations: EMD-CCA, ensemble EMD-CCA; EMD-CCA, empirical mode decomposition-canonical correlation analysis; VMD-FBCCA, variational mode decomposition–based filter bank canonical correlation analysis.
    Details are in the caption following the image
    FIGURE 4
    Open in figure viewerPowerPoint

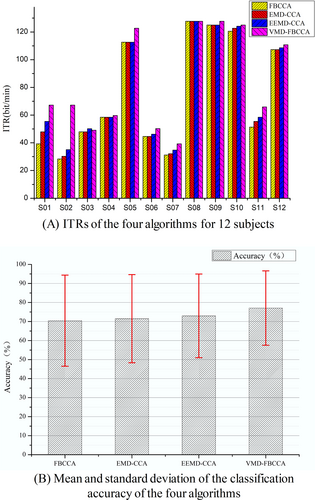
    Comparison of the results of four algorithms.

    Due to the high accuracy of S05, S08, S09, S10, and S12 in FBCCA, the accuracy of VMD-FBCCA did not change substantially, remaining between 90% and 100%. However, the optimization effects were more significant for S01, S02, and S11, for which the accuracy increased by 20%, 29.17%, and 10%, respectively. In addition, for S06 and S07, the accuracy increased by 4.17% and 6.67%, respectively. The optimization effect for S03 and S04 was not significant, which may be related to the subject's state in the experiment or a poor response to SSVEP.

    Except for S03, the accuracy of VMD-FBCCA is higher than that of EEMD-CCA in all subjects. Moreover, the average recognition accuracy and ITR of the VMD-FBCCA algorithm are higher than for the other three methods. Especially compared with the FBCCA algorithm, VMD-FBCCA achieved a substantial improvement, with an average accuracy improvement of 6.66 % $6.66\%$ . For S02, the accuracy improved by 29.17 % $29.17\%$ , with an average ITR improvement of 9.86 bits/min. Thus, the VMD-FBCCA algorithm is both accurate and efficient.

    Perfect scores of 100.00 were obtained for subjects S08, S09, and S10 by multiple algorithms. This is because these subjects had strong EEG signals with pronounced SSVEP responses that are easy to recognize. These results indicate the great variability in the difficulty of recognizing SSVEP responses between different subjects.

    To avoid generalizing individual results, we conducted statistical analysis on the results of 12 subjects for all four algorithms, and we calculated the average classification accuracy and standard deviation. In Table 1, the “AVG” is the average classification accuracy, and “STD” means standard deviation. They are shown in Figure 4B, in which the bar represents the average accuracy and the T-line is the standard deviation. It can be seen that the average classification accuracies of FBCCA, EMD-CCA, EEMD-CCA, and VMD-FBCCA are 70.42 % $70.42\%$ , 71.49 % $71.49\%$ , 72.97 % $72.97\%$ , and 77.08 % $77.08\%$ respectively. The corresponding standard deviations are 23.95 % $23.95\%$ , 23.15 % $23.15\%$ , 21.98 % $21.98\%$ , and 19.54 % $19.54\%$ , respectively. The average classification accuracy of VMD-FBCCA is higher than those of the other three algorithms, and its standard deviation is also smaller than theirs. Therefore, it can be deduced that the VMD-FBCCA algorithm is superior in performance to the other three algorithms.

    5 DISCUSSION

    5.1 VMD-FBCCA performance

    The VMD-FBCCA algorithm for decoding SSVEP signals can be understood as a process of decomposition, denoising, weight optimization, and reconstruction analysis of EEG signals. The EEG signal decomposition based on VMD uses a variational optimization method to determine the center frequency and bandwidth of the EEG signal in each channel. This method can easily obtain an adaptive narrowband IMF component, addressing challenges like end effects and modal component aliasing that can arise in methods like EMD. VMD effectively decomposes signals into multiple, relatively stable subsequences with varying frequency bandwidths.

    Here, the bandpass filtering and the VMD algorithm need to be addressed. The bandpass filtering commonly used in general preprocessing has stable amplitude–frequency characteristics inside and outside the pass band. However, there is a long transition band where SSVEP signals can easily be distorted. To identify the target frequency of the SSVEP, narrowband IMF components are more suitable for identification through correlation analysis. In addition, all modes decomposed by VMD contain the main signal modes and noise modes, and by reconstructing the main signal modes, the noise artifact can be effectively removed, which can make up for the lack of bandpass filtering.

    By comparing the recognition accuracy and ITR performance of VMD-FBCCA and the other three algorithms in Table 1 and Figure 4A, it can be seen that the VMD-FBCCA algorithm is superior to the other three algorithms, especially the FBCCA algorithm. This is because VMD has a remarkable noise reduction impact on the decomposition of EEG signals, enhancing both the signal-to-noise ratio and the recognition accuracy achieved after IMF weight optimization by the PSO algorithm.

    5.2 Discussion of PSO optimizational results

    In this paper, the PSO algorithm employs the recognition error rate as its fitness function, with the weight values serving as the particles. Through iterative optimization, the optimal weight coefficients of the IMFs are obtained. As illustrated in Figure 2, under the optimization process of the PSO algorithm, the recognition error rate continuously decreases and converges within dozens of iterations.

    PSO guides the IMF weight values to evolve toward those that minimize the error. After PSO completes the optimization of the IMF reconstruction parameters, it will ensure that the classification error of FBCCA is minimized. Throughout the entire process, the VMD algorithm itself cannot distinguish between the components of SSVEPs and noise but relies on the parameters optimized by PSO to complete the weighting of different components. It can be considered that the PSO algorithm, as a bridge between VMD and FBCCA, organically combines the two methods. The recognition accuracy of VMD-FBCCA for SSVEP signals has been improved, further demonstrating that the PSO algorithm has a positive effect on weight optimization.

    Because the SSVEP signal in the experiment is continuously stable in the 8–16 Hz frequency band, whereas the spontaneous α $\alpha $ rhythm is randomly unstable in the 8–13 Hz frequency band and the β $\beta $ rhythm is randomly unstable in the 13–30 Hz frequency band. The frequency coverage overlap between SSVEP and α $\alpha $ and β $\beta $ rhythm EEG signals will affect the characteristic frequency of the SSVEP.

    Figure 5 shows the PSD of the original and reconstructed EEGs for subject S02. Comparing Figure 5A,B, it can be seen that the EEG signal reconstructed by VMD-FBCCA weakens the SSVEP signal in the 1–8 Hz band and enhances the SSVEP signal in the 8–30 Hz band. The IMF weight changes of 11 and 22 Hz are especially pronounced. The same weakening and enhancing phenomenon was present for the other subjects.

    Details are in the caption following the image
    FIGURE 5
    Open in figure viewerPowerPoint

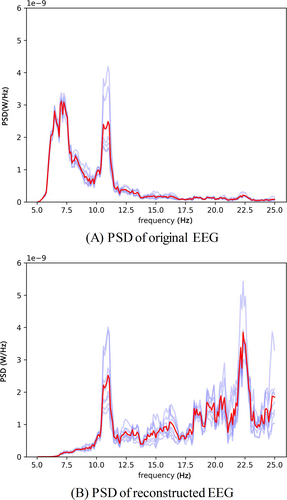
    PSD of original and reconstructed EEGs from S02. EEGs, electroencephalography; PSD, power spectral density.

    From the IMF component weight optimization results in Section 4.3, it can be seen that the IMF weights of SSVEP target rhythms are relatively large after optimization with the PSO algorithm and that the recognition accuracy of VMD-FBCCA on SSVEP signals is improved. It is verified further that optimizing EEG signals can improve the recognition accuracy.

    In the training phase of this algorithm, we set the classification error of FBCCA as the fitness function for PSO. Therefore, in the optimization process, the PSO algorithm will guide the IMF weights to evolve toward the values that minimize error. After PSO completes the optimization of the IMF reconstruction parameters, it will ensure that the FBCCA classification achieves maximum accuracy. Throughout the entire process, the VMD algorithm itself cannot distinguish between the SSVEP and noise components but relies on the parameters optimized by PSO to complete the weighting of different components.

    6 CONCLUSION

    This paper proposes the VMD-FBCCA algorithm to address the problem of overlapping frequency coverage between evoked and spontaneous EEG signals, which affects the characteristic frequency of SSVEP and thereby reduces the recognition accuracy of BCI systems. First, the EEG signals of different channels are decomposed into K $K$ IMF components with different central frequencies by VMD. Then, PSO is employed to optimize the weight of each IMF, and the optimized weights are used to reconstruct the EEG signal. Finally, FBCCA is used to recognize and classify the reconstructed EEG signals.

    The proposed VMD-FBCCA algorithm is tested on data from a BCI competition, and the experimental results demonstrate that it outperforms other algorithms. This algorithm combines the adaptability of VMD and the training-free advantages of FBCCA. In addition, PSO is used to optimize the weights of IMFs in different frequency bands to better distinguish SSVEPs from spontaneous EEG signals and improve the SSVEP recognition accuracy.

    The proposed algorithm has the potential to lead to improved BCI systems, and it offers a novel perspective for SSVEP-BCI research. Future research will emphasize enhancing the robustness of the VMD-FBCCA algorithm and refining the reference signal to boost its performance. Additionally, we aim to apply this algorithm to the development of SSVEP-BCI systems.

    AUTHOR CONTRIBUTIONS

    Ping Tan: Funding acquisition; investigation; methodology; project administration; supervision; writing–review & editing. Fengsheng Wang: Writing–original draft. Kaijun Zhou: Resources; validation. Yi Shen: Visualization.

    ACKNOWLEDGMENTS

    This work was supported by National Social Science Found of China (19BGL111), Key Project of Xiangjiang Laboratory (23XJ02006, 24XJJCYJ01001), and Scientific Research Project of the Education Department of Hunan Province (23A0470).

      CONFLICT OF INTEREST STATEMENT

      The authors declare that they have no conflicts of interest.

      ETHICS STATEMENT

      The experimental dataset utilized in this study is derived from the BCI Controlled Robot Contest held during the World Robot Contest in 2021,29 ethics approval was not needed in this study.

      DATA AVAILABILITY STATEMENT

      All data used to support the findings of this study are included within the article. The data can be obtained from the corresponding author upon request.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.