Das Distortion/Interaction-Activation-Strain-Modell zur Analyse von Reaktionsgeschwindigkeiten
Abstract
Das Activation-Strain- oder Distortion/Interaction-Modell ist ein Instrument zur Analyse von Aktivierungsbarrieren und damit von Reaktionsgeschwindigkeiten. Für eine bimolekulare Reaktion ergibt sich die Aktivierungsenergie aus der Summe der Energien, die für die Deformation der Grundzustandsgeometrie der Reaktanten benötigt wird, um die Geometrie des Übergangszustands anzunehmen, plus der Wechselwirkungsenergie zwischen diesen deformierten Reaktanten. Die mit der Deformation assoziierte Energie wird “activation strain” (Aktivierungsspannung) oder “distortion energy” (Deformationsenergie) genannt. Diese Energie bildet den Hauptbeitrag zur Aktivierungsbarriere. Der Übergangszustand wird erreicht, wenn die stabilisierende Wechselwirkung die Aktivierungsspannung überwindet. Die Verlaufsanalyse dieser Energien gibt Einblicke in die reaktivitätsbestimmenden physikalischen Faktoren. Anwendungsbeispiele für das Modell sind die Analyse von Substitutions- und Eliminierungsreaktionen sowie Cycloadditionen.
Die chemische Bindung und Reaktivität zu verstehen, ist bereits seit ihrem Anfang vor fast einem Jahrhundert eines der Hauptziele der theoretischen Chemie. Unser Mentor Roald Hoffmann hat wie kein anderer zum Verständnis der reaktivitätsbestimmenden Faktoren auf der Grundlage von Molekülorbitalen beigetragen. Unsere Gruppen haben unabhängig voneinander das Distortion/Interaction- oder Activation-Strain-Modell entwickelt. Dieser Aufsatz führt dieses Modell ein und beschreibt seine Anwendung auf viele unterschiedliche Gebiete der Chemie.
1. Reaktivitätsmodelle und Simulation
Seit den bahnbrechenden Arbeiten von Eyring und Polanyi wurden mehrere theoretische Reaktivitätsmodelle entwickelt. Einige der wichtigsten Modelle in der organischen Chemie sind die Grenzorbitaltheorie (FMO-Theorie, von “frontier molecular orbital”),1, 2 die Marcus-Theorie3 oder das “Curve-Crossing”-Modell in der “Valence-Bond”(VB)-Theorie.4 Fukuis FMO-Theorie5a und die Woodward-Hoffmann-Theorie führten zu einer weiten Verbreitung quantenchemischer Modelle unter organisch-chemischen Experimentatoren, die sich zuvor auf zuverlässige empirische Modelle verlassen hatten.
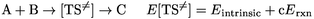(1)Im VB-“Curve-Crossing”-Modell werden Trends in der Barrierehöhe mithilfe der relativen Energien von Reaktanten- und Produktzuständen des Gesamtsystems sowie deren wechselseitiger Resonanz, wiederum im Gesamtsystem, beschrieben, sei es auf der Seite der Reaktanten [A,B] oder der Seite der Produkte [C] [siehe Gl. (1)].4 Das VB-Curve-Crossing-Modell stellt die Energie der Reaktanten- und Produkt-Zustände sowie deren gegenseitige Resonanz in direkte Beziehung zur elektronischen Struktur. Das hat den Vorteil, dass dieses Modell Fragen beantworten kann, z. B. weshalb Zustände sich in ihrer Energie unterscheiden (d. h., wieso eine Barriere niedrig oder hoch ist) und unter welchen Bedingungen eine beträchtliche Resonanzstabilisierung des Übergangszustandes (ÜZ) zu erwarten ist. Das VB-“Curve-Crossing”-Modell unterscheidet sich von unserem Modell, da es die Reaktivität aus der Sicht des Gesamtsystems betrachtet (im Reaktanten-, ÜZ- und Produkt-Zustand). Trotzdem ist es mit unserem Modell in der Grundidee artverwandt. Insbesondere strebt das VB-Curve-Crossing-Modell ebenfalls die Erstellung eines ursächlichen Zusammenhangs zwischen der elektronischen Struktur der reagierenden Spezies und der Höhe der Reaktionsbarriere an. Das VB-“Curve-Crossing”-Modell hat sich zu einem Hauptkonzept in der Reaktivitätstheorie entwickelt und findet zahlreiche Anwendungen in der organischen, metallorganischen und anorganischen Chemie.4d–4k Shaik, Schwarz und Mitarbeiter4i–4k haben beispielsweise in eleganter Weise gezeigt, wie das VB-“Curve-Crossing”-Modell – Hand in Hand mit unserem Modell – das Entstehen sowie den Trend in Aktivierungsspannungs- und ÜZ-Wechselwirkungstermen bei H-Atom-Transfer-Reaktionen beschreibt.
Wir haben einen anderen Ansatz entwickelt. Dieser beschreibt und erklärt die chemische Reaktivität aus Sicht der ursprünglichen Reaktanten und mit den Energien, die mit ihrer Deformation assoziiert sind, sowie mit der Veränderung der elektronischen Energie beim Erreichen des Übergangszustandes.6, 7 Hoffmann, und zuvor Fukui,5 nutzten die Grenzorbital(FMO)-Theorie zur näherungsweisen Beschreibung der Wechselwirkung zwischen Molekülen, aber vernachlässigten im Allgemeinen die geometrische Deformation, welche ebenfalls mit der Reaktion einhergeht.
Unser Modell stellt eine bedeutende Erweiterung des ursprünglichen FMO-Modells und der Rolle, die Symmetrie und Orbitalwechselwirkung darin spielen, dar.6, 7 Es schließt, anders als die FMO-Theorie, all diejenigen Reaktionen ein, die sich nicht durch Symmetrieprinzipien erfassen lassen.8 Die überwiegende Mehrheit an vorstellbaren chemischen Reaktionen ist symmetrieerlaubt, sie laufen jedoch mit geringer Effizienz oder überhaupt nicht ab. Der Grund für diese Diskrepanz zwischen dem ursprünglichem FMO-Modell und Experiment ist nicht eine vermeintliche Abweichung des tatsächlichen Reaktionsmechanismus von dem in der Theorie angenommenen synchronen, hochsymmetrischen Reaktionspfad. Tatsächlich verlaufen asynchrone Transformationsmoden in der Regel über flachere Potentialhyperflächen als erzwungen symmetrische Pfade.9 Die erwähnten Diskrepanzen werden ebenfalls in den meisten Fällen nicht durch subtilere Besonderheiten im Bindungsmechanismus verursacht, deren Analyse nur durch quantitativere Rechenmethoden zugänglich wäre.10
(2)Unser Modell zur Beschreibung von chemischer Reaktivität enthüllt die physikalischen Faktoren, die die unterschiedlichen Höhen von Reaktionsbarrieren und Reaktivitätstrends bei Strukturmodifikationen bestimmen. Ziel dieses Aufsatzes ist es zunächst nicht nur, eine detaillierte Beschreibung des Modells und dessen zugrundeliegender Konzepte zu liefern, sondern dem Leser auch eine Anleitung zur Berechnung an die Hand zu geben. Darauf folgen verschiedene Anwendungsbeispiele aus den Bereichen der organischen und anorganischen Chemie, mit dessen Diskussion den Konzepten Leben eingehaucht werden soll.
2. Das Activation-Strain- oder Distortion/Interaction-Modell
(3)
Das Activation-Strain-Modell am Beispiel einer metallvermittelten C-X-Bindungsaktivierung: 
[Reaktant 1]+ 
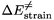[Reaktant 2]+
.
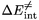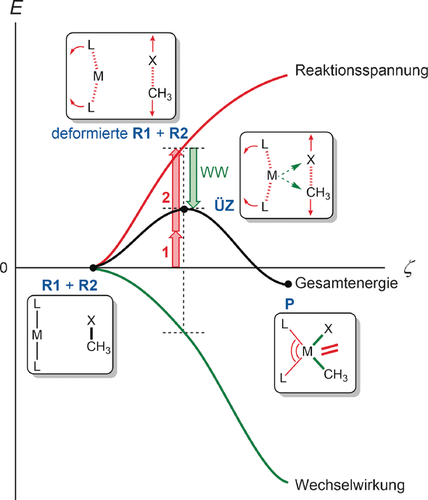
Die Reaktionsspannung ΔEstrain(ζ) wird von der Starrheit der Reaktanten bestimmt, z. B. von der Stärke der zu dissoziierenden Bindungen oder der Flexibilität von Bindungswinkeln, die verkleinert oder vergrößert werden. Die Reaktionsspannung hängt jedoch auch von der Art des Reaktionsmechanismus ab. Dieser bestimmt nämlich, wie viele Bindungen gebrochen werden und in welchem Ausmaß Gruppen umgeordnet werden müssen. Wie wir später sehen werden, geht die nukleophile Substitution mit weniger Deformation einher als die konkurrierende E2-Eliminierung. Aus diesem Grund sind das Deformationsausmaß und die Reaktionsspannung charakteristisch für einen bestimmten Reaktionspfad. In der Regel ist ΔEstrain(ζ) positiv, d. h. destabilisierend, und deshalb ein Faktor, der zur Entstehung einer Aktivierungsbarriere beiträgt. Dieser Term kann weiter in die individuellen Beiträge aufgegliedert werden (rote 1 und 2 in Abbildung 1), die von den am Prozess beteiligten Reaktanten herrühren.
Die Wechselwirkungsenergie ΔEint(ζ) zwischen den Reaktanten ist abhängig von ihrer elektronischen Struktur und von der Art, wie sich die Reaktanten bei Annäherung zueinander orientieren. Damit ist dieser Term auf die Bindungseigenschaft und die Wechselwirkung zwischen den in der Reaktionsfolge zunehmend deformierten Reaktanten zurückzuführen. Der Bindungsmechanismus, welcher der Wechselwirkungsenergie ΔEint(ζ) zugrundeliegt, kann unter Zuhilfenahme einer Energiedekompositionsanalyse (“energy decomposition analysis”, EDA) weiter im Kontext des Kohn-Sham-MO-Modells analysiert werden.10, 11 Die EDA quantifiziert die Terme für die elektrostatische Wechselwirkung, die Pauli-Abstoßung (Orbitalwechselwirkung zwischen spingleichen Elektronen) und stabilisierende Orbitalwechselwirkungen, beispielweise HOMO-LUMO-Wechselwirkungen, welche die Basis für Fukuis Grenzorbitaltheorie bilden. Bemerkenswert in diesem Zusammenhang ist, dass die EDA exakte Werte liefert, d. h. dass keine zusätzlichen Näherungen in der Berechnung (z. B. mit ZORA-OLYP/TZ2P) eingeführt werden müssen:10 Die Summe der Terme in der EDA ergibt exakt die Wechselwirkungsenergie bei gegebenem Theorieniveau. Das gilt für schwache Wechselwirkungen ebenso wie für starke chemische Bindungen.10 In den meisten Fällen ist ΔEint(ζ) negativ, d. h. stabilisierend, und damit ein direkter Gegenspieler der Reaktionsspannung ΔEstrain(ζ). Damit reduziert die Wechselwirkungsenergie meist eine von ΔEstrain(ζ) hervorgerufene Reaktionsbarriere. Es gibt jedoch Ausnahmen von dieser Regel: So ist für einige Cycloadditionen die Wechselwirkungsenergie zu Beginn der Reaktion positiv, also destabilisierend.
(4)Die Reaktionskoordinate ζ wird normalerweise als intrinsische Reaktionskoordinate (“intrinsic reaction coordinate”, IRC) mithilfe der “Steepest-Descent”-Methode ermittelt.12 Sie kann auf einen geeigneten kritischen geometrischen Parameter projiziert werden.13 Die Länge der Kohlenstoff-Halogen-Bindung (C-X), die bei einer oxidativen Addition gebrochen wird, kann z. B. einen solchen kritischen Parameter darstellen (Abbildung 1). Der kritische Parameter ζ ist immer entlang der x-Achse eines Aktivierungsspannungsdiagrammes (ASD) definiert und zeigt den Verlauf von ΔE(ζ), ΔEstrain(ζ) und ΔEint(ζ) als Funktion des Reaktionsfortschrittes.
. Deshalb gilt Gl. 5.
(5)Die Terme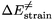 
und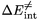 
des ÜZ müssen mit größter Sorgfalt interpretiert werden, da der optimierte ÜZ einen Kompromiss aus der Deformationsenergie ΔEstrain(ζ) und der Wechselwirkungsenergie ΔEint(ζ) darstellt. Dieser Sachverhalt macht deutlich, warum es ratsam ist, eine Verlaufsanalyse der beiden Komponenten entlang der Reaktionskoordinate durchzuführen. Eine Fokussierung auf den Übergangszustand allein (d. h. eine Punktanalyse des ÜZs) kann irreführende Ergebnisse liefern! Die Analyse entlang des gesamten Verlaufes der Reaktionskoordinate ist daher immer der sicherste Weg, um den Ursprung der Aktivierungsenergie zu verstehen.
Dies wird am Beispiel einer bimolekularen nukleophilen Substitutionsreaktion (SN2) besonders deutlich. Abbildung 2 zeigt das idealisierte Aktivierungsspannungsdiagramm (ASD) für eine prototypische Gasphasenreaktion, die nach einem SN2-Mechanismus abläuft. Eine Vielzahl von realen Beispielen kann auf diese Diagramme, die auf SN2-Reaktionen von Halogeniden mit Methylhalogeniden (berechnet mit ZORA-OLYP/TZ2P) basieren, bezogen werden.14 Die schwarzen Kurven in Abbildung 2 a und 2 b repräsentieren das ASD für ein Referenzsystem mit moderatem Nukleophil X− bzw. moderater Abgangsgruppe Y. Die grünen Kurven in Abbildung 2 a verdeutlichen, wie ein besseres Nukleophil durch eine Verstärkung der Wechselwirkung an jedem beliebigen Punkt des Reaktionspfades die SN2-Reaktionsbarriere verringern kann. Diese stärkere Wechselwirkung beruht auf der höheren Lewis-Basizität des stärkeren Nukleophils in der Gasphase. Dem gegenüber steht der Verlauf der roten Kurven in Abbildung 2 b, hier zeigt sich, dass eine schwache Abgangsgruppe die SN2-Reaktionsbarriere erhöht, da die Reaktionsspannungskurve destabilisiert wird. Der energetische Aufwand für die Streckung ist bei einer starken C-Y-Bindung höher als bei einer schwächeren. Diese Befunde sind dankenswerterweise in Einklang mit einer frühen VB-“Curve-Crossing”-Analyse von SN2-Reaktionen, die von Mitchel, Schlegel, Shaik und Wolfe durchgeführt wurde.4d
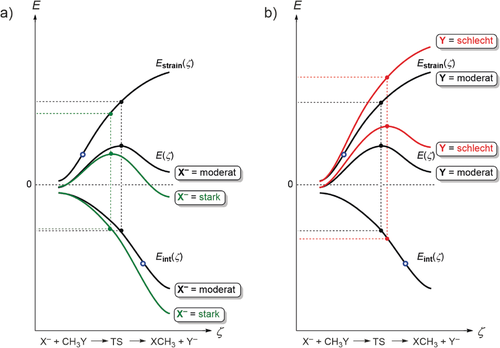
Aktivierungsspannungsdiagramm (ASD) für SN2-Reaktionen, in dem Übergangszustände (geschlossene Punkte) sowie Wendepunkte (blaue Kreise) gezeigt werden. In (a) und (b) stehen die schwarze Kurven für das gleiche Referenzsystem mit einem moderaten Nukleophil X− und einer moderaten Abgangsgruppe Y. In (a) zeigen die grünen Kurven den Effekt eines Wechsels zu einem stärkeren Nukleophil unter Beibehaltung der moderaten Abgangsgruppe. In (b) zeigen die roten Kurven den Effekt eines Wechsels zu einer schlechteren Abgangsgruppe Y unter Beibehaltung des moderaten Nukleophils.
Wichtig ist jedoch im Fall des stärkeren Nukleophils, dass eine Punktanalyse der entsprechenden Übergangszustände irrtümlicherweise die niedrigere SN2-Reaktionsbarriere mit einer suggerierten, geringeren Deformation des Substrates erklären würde (Abbildung 2 a). Eine genaue Inspektion des gesamten ASD ergibt jedoch zweifelsfrei, dass sich der Verlauf der Reaktionsspannungen entlang der Reaktionskoordinate ζ für beide Reaktionen nicht unterscheidet. In beiden Reaktionen wird die Deformation von der Dehnung und dem Bindungsbruch ein und derselben C-Y-Bindung in ein und demselben Methylhalogenid hervorgerufen. Wie bereits erwähnt, ist es die stabilisierte Wechselwirkungskurve ΔEint(ζ), die das energetisch niedrigere Reaktionsprofil E(ζ) und die niedrigere Reaktionsbarriere im Fall des stärkeren Nukleophils liefert. Der Grund, weshalb die Punktanalyse des ÜZ eine konträre Erklärung liefert, ist die Verschiebung des ÜZ der SN2-Reaktion für das moderat (d. h. schwächer) wechselwirkende Nukleophil zur Produktseite. Dies ist durch die schwächere und damit flachere Wechselwirkungskurve bedingt, die dafür sorgt, dass Gl. (4) bei unveränderter Reaktionsspannungskurve erst zu einem späteren Zeitpunkt, d. h. an einem Punkt, an dem auch ΔEstrain(ζ) abflacht, erfüllt ist.
Unser Modell ist in der Lage, sowohl den physikalischen Mechanismus einer linearen Gibbs-Energie-Beziehung zwischen den Aktivierungsenergien und den Reaktionsenergien15 zu ergründen, als auch den Ursprung des Hammond-Postulates zu erklären.16 Eine weniger stark stabilisierende Wechselwirkungskurve wirkt sich auf die Erhöhung der Reaktionsbarriere aus und macht die Reaktion auch endothermer. Jedoch führt eine weniger stabilisierende Wechselwirkung auch zu einer Verschiebung des ÜZ nach rechts und macht diesen produktähnlicher. Mit anderen Worten ausgedrückt wird das Hammond-Postulat damit zu einem hinlänglich bekannten Prinzip. Auch Abweichungen vom Postulat können leicht verstanden werden; sie resultieren aus irregulären Kurvenverläufen, die entweder in der Reaktionsspannungs- oder in der Wechselwirkungskurve auftreten und von speziellen sterischen oder elektronischen Bedingungen hervorgerufen werden.
3. Protokoll für eine Reaktivitätsanalyse
Bevor wir uns einigen Anwendungsbeispielen zuwenden, möchten wir die praktische Herangehensweise erläutern. Eine Analyseprozedur besteht aus den folgenden drei Schritten:
Als erstes müssen alle relevanten stationären Zustände (Reaktanten, ÜZ, Produkte) berechnet werden, d. h., es muss die mit dem elementaren Reaktionsschritt verbundene intrinsische Reaktionskoordinate (IRC) identifiziert werden. Die Reaktion kann entweder direkt von Reaktanten über den ÜZ zu den Produkten verlaufen oder – sofern ein schwach wechselwirkender Reaktantenkomplex existiert – über diesen zum ÜZ und zu den Produkten oder zu einem schwach wechselwirkenden Produktkomplex. Im letzteren Fall beginnt das Reaktionsprofil energetisch an einem Punkt, an dem die Gesamtenergie ΔE(ζ) bereits etwas unterhalb der separierten Reaktantenenergien liegt und die Reaktionsspannungskurve (oder Deformations-) ΔEstrain(ζ) und die Wechselwirkungskurve ΔEint(ζ) bereits positive bzw. negative Werte annehmen. Auch kann bereits an diesen Punkt die Reaktion den ersten moderaten Schritt in Bezug auf den kritischen Geometrieparameter vollziehen, also beispielweise mit einem Bindungsbruch beginnen. Ein typisches Beispiel ist das Aktivierungsspannungsdiagramm (ASD) für die SN2-Reaktion in Abbildung 2.
In einem zweiten Schritt sollte eine physikalisch vernünftige Projektion der IRC gefunden werden.13 Hierbei besteht einiger Spielraum, denn die Wahl der IRC ist nicht eine Frage von richtig oder falsch, es ist vielmehr eine Frage von hilfreich oder unbrauchbar. Die IRC ist eine komplexe Kombination von geometrischen Parametern, die die Interpretation erschweren kann. Die Bewegung flexibler Gruppen steht beispielweise in keiner kritischen Beziehung zu den geometrischen Parametern, die die Reaktion charakterisieren, wie Bindungsbrüche und -knüpfungsvorgänge. Dennoch können sie einen ausreichend großen, und damit störenden Effekt auf die Werte und die Änderungsrate der IRC haben. Damit sowohl Ausgangs- als auch Endwerte wohldefiniert sind und eine konsistente Vergleichbarkeit innerhalb einer Serie von analogen Reaktion gegeben ist, ist es hilfreich, wenn nicht entscheidend, die IRC auf den tatsächlichen kritischen Geometrieparameter zu projizieren. Auf diese Weise lassen sich die Energien und deren Komponenten an jeden Punkt entlang der IRC darstellen, so kann ΔE(ζ), ΔEstrain(ζ) und ΔEint(ζ) als eine Funktion des Wertes beschrieben werden, den der kritische geometrische Parameter ζ an diesem IRC-Punkt annimmt. Ein konkretes Beispiel ist die die metallvermittelte C-X-Bindungsaktivierung in einer oxidativen Addition: Hier wäre die Projektion der IRC in die Dehnung der C-X-Bindung des Substrates relativ zur Bindungslänge in dessen Gleichgewichtsstruktur des isolierten Substrates eine ausgezeichnete Wahl.13
Der dritte und letzte Schritt besteht in der Evaluierung der Reaktionsspannung ΔEstrain(ζ) und der Wechselwirkungsenergien ΔEint(ζ) durch zwei zusätzliche Einzelpunktberechnungen an jedem Zwischenschritt der IRC: eine für jeden der beiden einzelnen Reaktanten in der Geometrie, die sie an diesem IRC-Punkt annehmen.
4. Anwendungen in der Chemie
4.1. E2- und SN2-Reaktionen
(6 a)
(6 b)In einem Reaktionssystem aus einer Base X− und einem Substrat, welches die Abgangsgruppe Y und ein β-Proton aufweist, konkurriert die E2-Eliminierung stets mit der SN2-Substitution. Um das Ergebnis der Reaktion kontrollieren zu können, muss eine Reaktion schneller als die andere verlaufen. Das kann erreicht werden, indem entweder eine Reaktion beschleunigt oder die andere Reaktion verlangsamt wird. Im Folgenden werden wir dies anhand von verallgemeinerten Beispielen für die E2- und SN2-Reaktionen verdeutlichen. Zu diesem Zweck haben wir alle wesentlichen Erkenntnisse aus einer Reihe von aktuellen DFT-Studien kombiniert.6a, 14, 17, 18 Wir haben uns ferner vergewissert, dass die gefundenen Trends für E2 und SN2, die mit BP86/TZ2P//Xα/DZP berechnet wurden und Lit. 18a,18b entnommen sind, mit den Trends übereinstimmen, die mit moderneren Methoden (ZORA-OLYP/TZ2P//ZORA-OLYP/TZ2P) berechnet wurden.18d
SN2-Reaktionen können entweder durch eine Steigerung der stabilisierenden Wechselwirkung ΔEint(ζ) oder durch die Reduzierung der Deformation im Übergangszustand ΔEstrain(ζ) beschleunigt werden. Die Schlüsselfunktion, die ΔEint(ζ) maßgeblich bestimmt, ist die Orbitalwechselwirkung zwischen dem HOMO des Nukleophils (Base, z. B. dem n p-AO des Halogenids) und dem σ*C-Y-LUMO des Substrats.14 Durch die Destabilisierung des HOMO des Nukleophils (z. B., beim Wechsel von X−=Cl− zu X−=F−),19 wird die Wechselwirkungskurve stabilisiert und die SN2-Reaktion beschleunigt (Abbildung 2 a: von den schwarzen zu den grünen Kurven). Mit anderen Worten ausgedrückt, ist die stärkere Lewis-Base auch das bessere Nukleophil. Die SN2-Reaktion kann ebenfalls beschleunigt werden, indem der Wechsel der Abgangsgruppe Y zu einer schwächeren C-Y-Bindung im Substrat führt (z. B. beim Wechsel von C-F zu C-Cl).20 Dies resultiert aus der geringeren Reaktionsspannung (Deformationsenergie) einer solchen Reaktion (Abbildung 2 b: von den roten zu den schwarzen Kurven). Es gibt zahllose andere Möglichkeiten, die Reaktionsspannung und die Wechselwirkung in SN2-Reaktionen zu verändern.17
Bei einem Substrat, welches sowohl eine Y Abgangsgruppe am Cα und ein Proton am Cβ [Gl. (6)] ausweist, besteht die Möglichkeit, dass sowohl eine Deprotonierung des Hβ, zu einer E2-Eliminierung [Gl. (6a)] führen kann, als auch ein nukleophiler Angriff am Cα zu einer SN2-Substitution [Gl. (6b)] führt. Wie Abbildung 3 a zeigt, haben beide Reaktionspfade sehr unterschiedliche und charakteristische Werte für die Deformationsenergie (Aktivierungsspannung). Hier konzentrieren wir uns auf die Analyse des ÜZ von vier Reaktionen: die E2- und SN2-Reaktionen einer starken und einer schwachen Base X− mit dem gleichen Substrat (CH3CH2Y).18
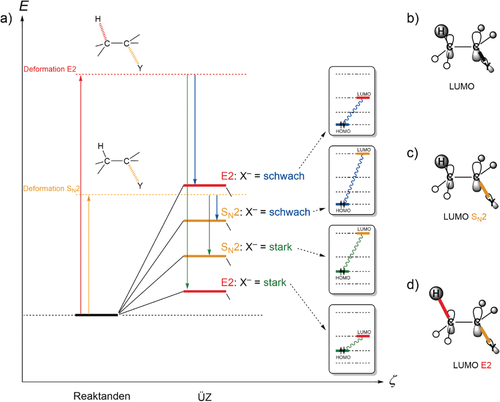
a) Schematisches Aktivierungsspannungsdiagramm für die vier Übergangszustände (ÜZ) von E2- und SN2-Reaktionen einer schwachen und starken Base X− (d. h., HOMO bei niedriger bzw. hoher Orbitalenergie) mit identischen Substraten (CH3CH2Y), wobei für jeden ÜZ der Base-Substrat-HOMO-LUMO-Abstand gezeigt wird. b) Das Substrat-LUMO ist Cα-Y- und Cβ-H-antibindend. c) SN2-Verzerrung reduziert die antibindende Cα-Y-Überlappung und senkt daher die LUMO-Energie. d) E2-Verzerrung senkt das Substrat-LUMO sogar noch stärker, weil die antibindenden Cα-Y- und Cβ-H-Überlappungen reduziert werden.
Die E2-Eliminierung weist die stärkere Deformation auf, denn zwei Bindungen werden gebrochen (Cα-Y und Cβ-H). Diese Reaktion ist somit mit einer relativ hohen Aktivierungsspannung assoziiert, unabhängig von der verwendeten Base X− (Abbildung 3 a). Dagegen ist die SN2-Substitution durch eine geringere Deformation charakterisiert, oder sie weist eine geringere Aktivierungsspannung auf, weil nur eine Bindung gebrochen wird (Cα-Y). Gleichzeitig haben die unterschiedlichen Deformationsgrade für die E2- und SN2-Reaktionspfade einen großen Effekt auf die elektronische Struktur des Substrates entlang des Reaktionsweges und auf den Übergangzustand im Besonderen. Das LUMO des Substrates hat antibindenden σ*-Charakter bezüglich der Cα-Y- und Cβ-H-Bindung (Abbildung 3 b).18 Als Konsequenz vermag die SN2-Deformation die antibindende Überlappung für Cα-Y zu verringern und so das LUMO energetisch zu stabilisieren (Abbildung 3 c). Die E2-Deformation stabilisiert das LUMO des Substrates jedoch noch stärker, denn beide antibindende Überlappungen in Cα-Y und Cβ-H werden reduziert (Abbildung 3 d). Das impliziert einen kleineren HOMO-LUMO-Abstand mit der Base oder Nukleophil, und dadurch werden die Wechselwirkungen im ÜZ der E2-Reaktion zwischen der Base und dem Substrat im Gegensatz zum SN2-Übergangszustand signifikant verstärkt. Anders ausgedrückt ist das deformierte E2-Substrat eine stärkere Lewis-Säure als das deformierte SN2-Substrat.
Diese Erkenntnisse erklären viele experimentelle Befunde8a, 21 und liefern darüber hinaus Designprinzipien. Wenn X− eine starke Lewis-Base ist, d. h. ein hochliegendes HOMO aufweist, kann die hohe E2-Aktivierungsspannung kompensiert werden, da der kleinere HOMO-LUMO-Abstand für eine stärker stabilisierende Base-Substrat-Wechselwirkung sorgt, die den E2-Übergangszustand unterhalb des ÜZ der SN2-Reaktion senken kann. Wenn X− jedoch eine schwache Lewis-Base ist, d. h. ein niedrigliegendes HOMO aufweist, kann die E2-Aktivierungsspannung nicht länger kompensiert werden, auch wenn die Wechselwirkung im E2-ÜZ immer noch stärker ist. Wird der HOMO-LUMO-Abstand zu groß, wird auch die Wechselwirkung im ÜZ zu gering, um noch einen Einfluss auf den Trend nehmen zu können, der nun von der Aktivierungsspannung vorgegeben wird und der den SN2-Reaktionspfad aufgrund der geringeren Deformation bevorzugt.
Wir können so also verstehen, warum eine starke Base protophil reagiert, während eine schwache Base als Nukleophil angreift. Der kleinere HOMO-LUMO-Abstand führt zu einer stabilisierenden Base-Substrat-Wechselwirkung, welche die Energie des E2-Übergangszustands unter die des ÜZ der SN2-Reaktion senkt. Der gleiche Reaktionsmechanismus erklärt auch, warum eine (stärkere) Solvatation die Verschiebung der Reaktivität vom protophilen zum nukleophilen Angriff bewirkt. In erster Linie ist das auf die von der Solvatation ausgelöste Abschwächung der Basizität von X− zurückzuführen: Dessen HOMO wird stabilisiert.18b Deshalb zeigen die gleichen oder ähnliche Reaktanten in der Gasphase häufig eine E2-Reaktivität, während sie in Lösung eine verstärkte Neigung zur SN2-Substitution aufweisen.
4.2. Nukleophile Additionen an Alkenen und Alkinen
Vor einigen Jahren haben wir die gesteigerte Reaktivität von elektronenarmen Alkinen im Vergleich zu Alkenen in nukleophilen Reaktionen erklärt. Während der Vergleich der Grenzorbitalenergien von Alkene und Alkinen eher auf eine größere Reaktivität von Alkene hindeutet, da sie eine niedrigere LUMO-Energie aufweisen, sind es jedoch die Alkine, die reaktiver sind. Der Grund dafür ist, dass die Alkine einfacher zu deformieren sind und die damit verbundene Verkleinerung des HOMO-LUMO-Abstandes zu einer gesteigerten Reaktivität der Alkine führt. Im Übergangszustand hat Acetylen eine niedrigere LUMO-Energie.22a Ungefähr zur selben Zeit konnten wir die Rolle der Deformation bei Didehydrobenzol und bei radikalischen Additionen an Alkene zeigen.22b,22c Die erste Anwendung dieses Modells zur Erklärung der Stereoselektivität bei Additionen an Carbonylverbindungen folgte wenig später.22d
4.3. Diels-Alder-Cycloadditionen: spannungsinduzierte oder deformationsbschleunigte Reaktionen?
Das Distortion/Interaction-Modell hat sich als besonders nützlich für die Erklärung von Cycloadditionsreaktivitäten erwiesen. Wir konnten zeigen, wie die Reaktivitäten in Diels-Alder-Cycloadditionen mit Ethen und in Reaktionen mit H2 für eine große Bandbreite aromatischer Kohlenwasserstoffe und Heterocyclen sehr eng mit der Deformationsenergie der Reaktion korrelieren.23 Abbildung 4 zeigt die Korrelation zwischen Aktivierungsenergien und Deformationsenergien (a) sowie Reaktionsenergien (b).
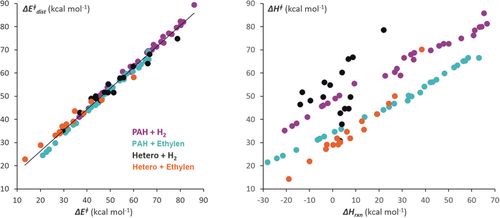
Korrelation zwischen berechneten Aktivierungsenergien von Diels-Alder-Reaktionen aromatischer Diene und Maleinsäureanhydrid mit Deformationsenergien (links) und Reaktionsenergien (rechts).
Die letztgenannte ist ein Beispiel für eine empirische Korrelation, die auf Dimroth zurückgeht, von Evans, Polanyi, Hammond, Jencks und anderen15 erklärt werden konnte und durch die Marcus-Theorie theoretisch gestützt wird.24
Es gibt einige Fälle, in denen die Aktivierungsenergie sowohl mit den Reaktionsenergien (d. h. für Evans-Polanyi-Situationen) als auch mit den Deformationsenergien korreliert. Diese Konstellation tritt auf, wenn die Deformationsenergie des Übergangszustands, oder die Aktivierungsspannung, ein konstanter Bestandteil der Deformation in den Produkten ist. Das ist nicht immer der Fall. In jüngsten Anwendungen des Distortion/Interaction-Modells zeigt sich eine exzellente Korrelation zwischen der Deformationsenergie des ÜZ und der Aktivierungsenergie, jedoch korrelieren die Reaktionsenergien nicht mit den Aktivierungsenergien.25 In Zusammenarbeit mit der experimentell arbeitenden Gruppe um Danishefsky hat unsere Gruppe (Paton et al.25a) Diels-Alder-Reaktionen zwischen Cyclopentadien und Cycloalkenonen, wie Cyclohexenon und Cyclopropenon, sowie dem acyclischen Pent-3-en-2-on untersucht. Die Übergangszustände dieser Reaktionen sind in Abbildung 5 dargestellt.
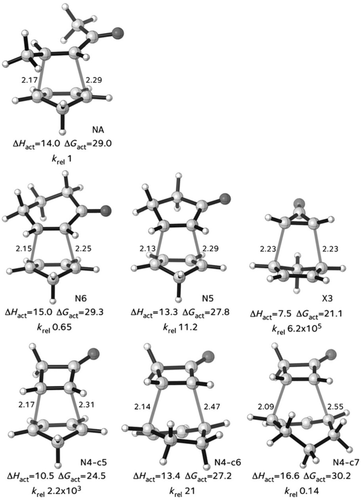
Übergangszustände von Diels-Alder-Reaktionen von Cyclopentadien mit Enonen, berechnet auf dem M06-2X-6-31G(d)-Niveau. Energien in kcal mol−1.25a.
Wir haben ebenfalls eine Reihe von Reaktionen der entsprechenden Cycloalkene mit verschiedenen Dienen untersucht.25b Abbildung 6 zeigt die Aktivierungsenergien der Cycloadditionen von Cycloalkenen und Cycloalkenonen mit Cyclopentadien, aufgetragen gegen ihre Deformationsenergien.
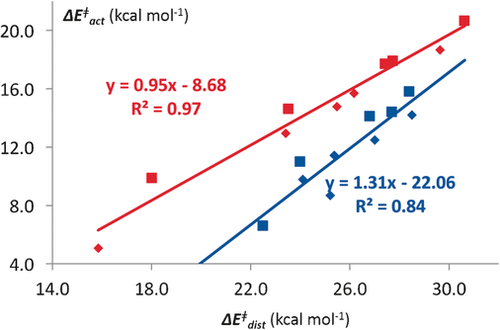
Korrelation zwischen Aktivierungsenergien und Deformationsenergien für Diels-Alder-Reaktionen von Cyclopentadien mit Cycloalkenen (rot) und Cycloalkenonen (blau), einschließlich exo- (kleine Symbols) und endo-Reaktivität (große Symbole).
Diese Korrelation ist ein Ergebnis der Spannung in den kleinen Ringen, aber resultiert maßgeblich nicht aus der größeren Exothermie dieser Reaktionen. Die Deformationsenergien der Übergangszustände korreliert sehr eng mit den Aktivierungsenergien,25 und aktuelle Untersuchungen aus unserer Gruppe legen nahe, dass diese Korrelation ein Ergebnis der unterschiedlichen Wechselwirkungsenergien ist, die eine erhebliche Verschiebung des Übergangzustandes bewirkt und in der Folge auch die Deformationsenergien des ÜZ verändert, ganz ähnlich, wie es bereits für SN2-Reaktionen diskutiert wurde (siehe Abbildung 2).14 Levandowski und Houk haben diese Studie auf substituierte Cyclopropene ausgedehnt.26
Andere Anwendungen des Distortion/Interaction-Modells finden sich in der Analyse der Cycloadditionen von Aziden an Norbornen27 und in einer interessanten Carbonyl-Olefin-Metathese, die von Lambert und Kollegen28 entdeckt wurde. Diese Beispiele zeigen, wie breit das Konzept auf Cycloadditionen angewendet werden kann.
Auf den Gebiet der Cycloadditionen an Fullerenen haben unsere beiden Gruppen zeigen können, wie gekrümmte Arene die Reaktivität im Gegensatz zu planaren polybenzoiden Arenen verstärken können.29 Gemeinsam mit den Gruppen um Fernandez und Solà haben wir die Reaktivität von Fullerenen in verschiedenen Reaktionsmechanismen unter Zuhilfenahme des Activation-Strain-Modells untersucht.29a So konnten wir den Ursprung der experimentell gefundenen Regioselektivität von [6,6]- über [5,6]-Bindungen in Diels-Alder-Cycloadditionen von C60 mit beispielsweise Cyclopentadien erklären. Diese kann auf die größere stabilisierende Wechselwirkung für den [6,6]-Reaktionspfad entlang der gesamten Reaktionskoordinate zurückgeführt werden und ist eine direkte Konsequenz des dreifach entarteten LUMO in C60, das den passenden π*C-C-Charakter für [6,6] aufweist, aber nicht für die [5,6]-Bindung. Wir haben die Diels-Alder-Reaktion von Butadien und drei 1,3-dipolaren Cycloadditionen an Polyacenen, Kohlenstoffnanoröhren und Fullerenen untersucht.29g Die Aktivierungsenergien wurden mit den Deformationsenergien für planare, gekrümmte und sphärische benzoide Kohlenwasserstoffe korreliert.
4.4. Dehydro-Diels-Alder-Reaktionen
In letzter Zeit gibt es, aufgrund der jüngster Studie von Hoye et al. zu Anwendungen in der Synthese, wieder ein gesteigertes Interesse an “Dehydro”-Cycloadditionen.30 Diese Reaktionstyp wurde ursprünglich theoretisch vorhergesagt und experimentell von Johnson und Mitarbeitern31 bestätigt. Neue Studien, die die Reaktion mithilfe der Dichtefunktionaltheorie untersuchen, stammen von Hoye und von der Gruppe um Houk.32 Unsere eigenen Ergebnisse zeigen für diese Reaktionen eine Korrelation zwischen dem Grad der Sättigung der Reaktanten, der Deformationsenergie und den Aktivierungsenergien. In der Abbildung 7 sind die untersuchten Reaktionen mit den Übergangszuständen für die entsprechenden konzertierten und schrittweisen Pfade dargestellt.
Mit (U)M06-2X/6-31+G(d,p)-optimierte Übergangszustände für die konzertierte und für die schrittweise Diels-Alder-Reaktion und analoge Dehydro-Reaktionen.
Die Tabelle 1 verdeutlicht, wie die Deformationsenergie der konzertierten Reaktionen mit Abnahme des Sättigungsgrades zunimmt, während die Tabelle 2 eine nahezu konstante Deformationsenergie für die diradikalischen Übergangzustände des schrittweisen Prozesses zeigt. Hierdurch gleichen sich die Energiebarrieren der beiden Mechanismen für die HDDA-Reaktion letztlich aneinander an. Bei weiterer Substitution wird der schrittweise Mechanismus bevorzugt.32
Nr. |
TS |
Eact |
Edist-4π |
Edist-2π |
Edist |
Eint |
Erxn |
|---|---|---|---|---|---|---|---|
1 |
TS-1 c |
19.6 |
18.8 |
7.4 |
26.1 |
−6.5 |
−47.6 |
2 |
TS-2 c |
21.2 |
17.1 |
10.3 |
27.4 |
−6.2 |
−61.8 |
3 |
TS-3 c |
27.3 |
24.3 |
10.6 |
34.9 |
−7.6 |
−18.6 |
4 |
TS-4 c |
29.5 |
22.2 |
14.0 |
36.2 |
−6.7 |
−30.0 |
5 |
TS-5 c |
33.9 |
32.8 |
11.4 |
44.3 |
−10.4 |
−4.4 |
6 |
TS-6 c |
36.0 |
29.2 |
14.0 |
43.2 |
−7.2 |
−57.3 |
Nr. |
TS |
Eact |
Edist-4π |
Edist-2π |
Edist |
Eint |
E(DR) |
E(TSs2) |
|---|---|---|---|---|---|---|---|---|
1 |
TS-1 s |
35.4 |
12.6 |
12.2 |
24.9 |
10.5 |
28.5 |
32.1 |
2 |
TS-2 s |
35.4 |
10.9 |
16.5 |
27.4 |
8.0 |
27.0 |
29.1 |
3 |
TS-3 s |
34.5 |
13.5 |
11.2 |
24.7 |
9.8 |
27.8 |
32.9 |
4 |
TS-4 s |
35.0 |
11.9 |
15.1 |
27.0 |
8.0 |
25.0 |
28.3 |
5 |
TS-5 s |
34.2 |
14.8 |
11.0 |
25.8 |
8.4 |
29.5 |
37.8 |
6 |
TS-6 s |
35.2 |
13.0 |
14.6 |
27.5 |
7.7 |
25.7 |
30.8 |
4.5. Cycloadditionen in der bioorthogonalen Chemie
Wir haben unser Modell zur Erklärung einer Vielzahl von bioorthogonalen Cycloadditionen herangezogen und um die Paarungen von Cycloadditionen vorherzusagen, die wechselseitig orthogonal sind.33, 34 Eine spannungsinduzierte Alkin-Azid-Cycloaddition (“strain-promoted alkyne–azide cycloaddition”, SPAAC) ist die kupferfreie Klick-Reaktion, die in verschiedenen Gebieten der Chemie, besonders aber in der bioorthogonalen Chemie Verwendung findet.33 In einer kombinierten experimentellen und theoretischen Studie mit der Gruppe um Van Delft konnten wir zeigen, dass die Geschwindigkeit schneller SPAAC-Reaktionen zwischen elektronenarmen Aziden (Ar-N3) mit Bicyclononin (BCN) von FMO-Wechselwirkungen mit inversem Elektronenbedarf (“inverse electron demand”, IED) bestimmt wird (Schema 1).33
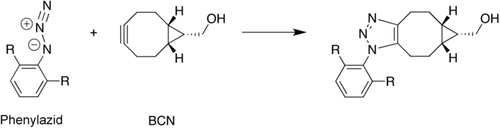
SPAAC-Reaktion von aromatischen Aziden mit Bicyclononin (BCN).
Die Aktivierungsspannungsanalyse zeigt, wie die Wechselwirkungen im ÜZ zunehmend stabilisierender werden, sobald elektronenziehende Substituenten (R) den elektronenarmen Charakter des Azides verstärken. Dies führt zu einer Absenkung der Barriere und in der Begleiterscheinung zu einer experimentell beobachteten Beschleunigung der Reaktion. Diesem Trend liegt die IED-FMO-Wechselwirkung zwischen dem π-bindenden HOMO und HOMO−1 des BCN-Moleküls und dem relativ niedrigliegenden LUMO des Azids zugrunde.
Ein sehr nützliches und von uns entdecktes Prinzip, welches ebenfalls mit dem Distortion/Interaction-Modell erklärt werden kann, ist die Verwendung intrinsisch reaktiver Cycloaddenden, die auch sterisch besonders anspruchsvoll sind.34 Sterischer Anspruch zeigt sich sehr oft in einer höheren Deformationsenergie. Andere Cycloaddenden können eine geringere intrinsische Reaktivität aufweisen, aber sterisch weniger anspruchsvoll sein. Ein gutes Beispiel ist die hohe intrinsische elektrophile Reaktivität von zweifach substituierten Tetrazinen, die durch ihr niedrigliegendes π*-Orbital hervorgerufen wird; diese Verbindungen haben, aufgrund ihrer beiden Arylsubstituenten, einen relativ hohen sterischen Anspruch. Dagegen sind Azide intrinsisch weniger reaktiv, dafür aber sehr viel weniger sterisch gehindert. Die experimentellen Befunde hierzu sind in der Abbildung 8 dargestellt.34d
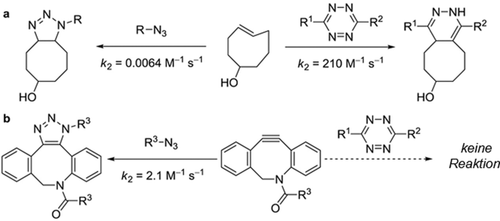
Beispiele von wechselseitig orthogonalen Reaktionen. (a) ist schnell für Tetrazine, nicht jedoch für Azide. (b) ist schnell für Azide, nicht jedoch für Tetrazine.34d.
Ein weiteres Beispiel dieser Art sei mit der Entwicklung neuer, auf Cyclopropen basierender bioorthogonaler Cycloaddenden illustriert.34e Sterisch anspruchsvolle 3,3-disubstituierte Cyclopropene reagieren mit hoch reaktiven, aber wenig sterisch anspruchsvollen 1,3-Diarylnitriliminen, jedoch findet mit sterisch anspruchsvollen Tetrazinen keine Reaktion statt. Tetrazine reagieren hingegen mit 1,3-disubstituierten Cyclopropenen.34e Diese Prinzipien wurden in einer Kooperation von uns mit Devaraj über 1,3-disubstitutierte Cyclopropene weiterentwickelt, in der die allgemeine Reaktivität von Tetrazinen gezeigt wurde.34f
Theoretische Studien auf der Basis des Distortion/Interaction-Modells und experimenteller Befunde führten zu einer neuen Klasse bioorthogonaler elektronenarmer Diene, den 1,2,4-Triazinen. Diese Verbindungen sind im zellulären Milieu wesentlich stabiler als Tetrazine. Dadurch können sie an nichtnatürliche Aminosäuren angebunden werden, die dann wiederum durch die Reaktion mit trans-Cyclooctenen in Proteine eingebunden werden können.34g
4.6. Andere pericyclische Reaktionen
In Zusammenarbeit mit der Gruppe um Fernandez haben wir Alder-En-Reaktion untersucht, die über einen sechsgliedrigen cyclischen aromatischen ÜZ verlaufen (Schema 2).35
Alder-En-Reaktion (XY ist z. B. C2H4, C2H2, CH2NH, CH2O).
Die Barriere der Reaktion wird durch die Aktivierungsspannung hervorgerufen, die die deformierten Reaktanten benötigen, um eine cyclische Geometrie anzunehmen, welche für eine aromatische Konjugation geeignet ist. Die Alder-En-Barriere kann durch die Beteiligung von Elementen der dritten Periode an der Doppelbindung des Enophils gesenkt werden. Unsere Aktivierungsspannungsanalyse zeigt, dass dieser Reaktivitätstrend auf die verringerte Überlappung des LUMO des Enophils mit der C-H-Bindung zurückzuführen ist, an der der Transfer des Wasserstoffatoms vom En zum Enophil stattfindet. In der Konsequenz ergibt sich entlang dieser Serie, dass die Spaltung der C-H-Bindung des Ens hinter den Knüpfung der neuen En-Enophil-C-C-Bindung zurückfällt. Das führt zu einer geringen Aktivierungsspannung im En-Reaktanten und damit zu einer geringeren Gesamtreaktionsbarriere.35
4.7. Homogene Katalyse
Die metallvermittelte C-X-Bindungsaktivierung spielt eine zentrale Rolle in vielen Prozessen der homogenen Katalyse.8 In mehreren Studien haben wir die physikalischen Faktoren untersucht, die Ligandeneffekte auf die Aktivität von d10-ML2-Komplexen in C-H-, C-C- und C-Halogen-Aktivierungsreaktionen haben. Diese Aktivierung stellt den selektivitätsbestimmenden Schritt in vielen Kreuzkupplungen dar.36, 37, 38 Hier werden wir uns bei unserer Aktivierungsspannungsanalyse auf den Bisswinkeleffekt konzentrieren.36a,36b Die Aktivierungsspannungsanalyse anderer Aspekte der metallvermittelten Bindungsaktivierung wird in Lit. 37 beschrieben. Der Bisswinkeleffekt ist experimentell gut untersucht; die Barriere der Bindungsaktivierung einer oxidativen Insertion in die C-X-Bindung an einem Metallzentrum ist geringer, wenn der L-M-L-Winkel in d10-ML2 kleiner als 180° ist. Beispielsweise kann dies bei der wichtigen Klasse der Palladium-Bisphosphankomplexe über ein Molekülgerüst erreicht werden, etwa indem eine Polymethylenbrücke die koordinierenden Phosphoratome näher zusammenbringt und fixiert.38 Durch Variation der Kettenlänge können Katalysatoren mit unterschiedlichen P-Pd-P-Bisswinkeln realisiert werden, die die Bindungsaktivierung mit hohen oder niedrigen Barrieren vollziehen. Dies wird in der Abbildung 9 a deutlich, in der die PES der Methan-C-H-Aktivierung mittels oxidativer Addition an ein Pd-Atom, an den prototypischen Pd(PH3)2-Komplex und an einen Pd[PH2(CH2)nPH2]-Chelatkomplex gezeigt wird. Im letztgenannten reduziert die kurze Bimethylenbrücke (n=2) den P-Pd-P-Bisswinkel von 180° zu 98°.37a,37b Wie in der Abbildung zu erkennen ist, erhört die Einführung der Liganden die Barriere. Jedoch führt die Reduzierung des Bisswinkels zu niedrigeren Barrieren.
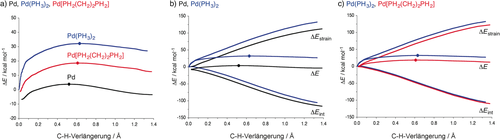
Potentialhyperflächen (a) und Aktivierungsspannungsdiagramme (b,c) der oxidativen Addition der Methan-C-H-Bindung an Pd (schwarz), Pd(PH3)2 (blau) und Pd[PH2(CH2)2PH2] (rot). Punkte zeigen die Lage des ÜZ.
Unsere Aktivierungsspannungsanalyse zeigt, dass die höhere Barriere, die aus der Einführung der Liganden resultiert, zu einem großen Anteil, aber nicht ausschließlich, auf die mehr destabilisierende Spannungskurve zurückzuführen ist (Abbildung 9 b).36a,36b Diese ist mit der Notwendigkeit zur Abwinkelung der Phosphanliganden assoziiert, sobald die zu aktivierende C-X-Bindung koordiniert wird. Die geringere Reaktionsbarrieren für die Komplexe mit kleineren Bisswinkeln resultieren aus einem weicheren Deformationsterm.36a,36b Der Grund, warum ein kleinerer Bisswinkel mit einer geringeren Deformationsenergie einhergeht, liegt in der Reduzierung der notwendigen Abwinkelung der Phosphanliganden, sobald das Substrat sich nähert. Das verhindert das Ansteigen des Deformationsenergieterms am Anfang der Reaktion, wie es für Pd(PH3)2 zu finden ist. Die Analyse zeigt deutlich, dass die niedrigere Barriere auf den geometrischen Effekt zurückzuführen ist, der durch den Bisswinkel hervorgerufen wird, und einen sterischen Effekt darstellt. Die stärkere Donation aus dem destabilisierenden dπ-Metallorbital des Katalysators trägt ebenfalls zu einer etwas stärkeren Katalysator-Substrat-Wechselwirkung bei, spielt aber eine untergeordnete Rolle. Interessanterweise kann die Deformationsenergie des Katalysators und damit die Reaktionsbarriere auch durch die Verwendung nichtchelatisierender Metall-Liganden-Kombinationen in d10-ML2 reduziert werden, wenn Liganden verwendet werden, die eine intrinsische Präferenz für gewinkelte L-M-L-Geometrien aufweisen. Das ist der Fall, wenn eine starke π-Rückbindung36c–36e vorliegt und/oder wenn nichtisotrope sterisch anspruchsvolle Liganden durch Dispersionswechselwirkungen zwischen ihren großen Oberflächen zusammengehalten werden.36f
Zusammen mit Merlic konnten wir mit unserem Distortion/Interaction-Modell die Änderung der Regioselektivität von Kreuzkupplungen unter Verwendung verschiedener Liganden erklären.39 Die Abbildungen 10 und 11 geben zwei Beispiele für die Regioselektivität zusammen mit den Deformations- und Wechselwirkungsenergien, die für diese Reaktionen berechnet wurden. Abbildung 10 zeigt ein Beispiel für eine deformationskontrollierte Reaktion, während Abbildung 11 ein Beispiel für eine wechselwirkungskontrollierte Reaktion zeigt.
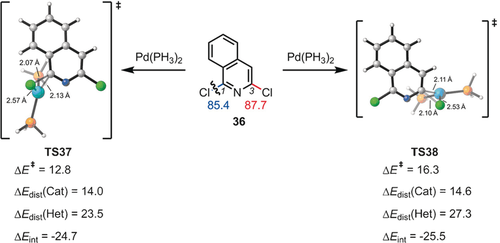
Energien und Distortion/Interaction-Analyse von Übergangszuständen (TS37 und TS38) bei der [Pd(PH3)2]-vermittelten oxidativen Addition der C-Cl-Bindung des Arylchlorids 36. Energien in kcal mol−1.
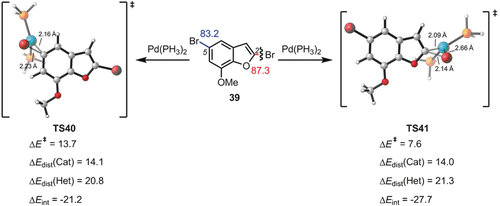
Energien und Distortion/Interaction-Analyse von Übergangszuständen (TS40 und TS41) bei der [Pd(PH3)2]-vermittelten oxidativen Addition der C-Br-Bindung des Arylbromids 39. Energien in kcal mol−1.
Der erste Fall lässt sich durch den leichteren Bindungsbruch der C-Cl-Bindung in einer sterisch anspruchsvollen Umgebung erklären, während das zweite Beispiel aufgrund des großen LUMO-Koeffizienten am C2-Atom zu einer stärkeren Wechselwirkung mit dem Pd-Nukleophil führt. Die Reaktivität einiger Iridium-katalysierter Suzuki-Reaktionen wurde ebenfalls untersucht und konnte mit dem Distortion/Interaction-Modell rationalisiert werden.40
4.8. Organokatalyse
In diesen Abschnitt möchten wir zwei Beispiele für die Anwendung unseres Distortion/Interaction- oder Activation-Strain-Modells in der Organokatalyse präsentieren, die zeigen, wie unser Modell zur Erklärung von Stereoselektivitäten genutzt werden kann. Häufig haben Übergangszustände eine nahezu identische sterische Umgebung, auch wenn sie sich signifikant in ihrer Energie unterscheiden. Dies wird dadurch verursacht, dass die Deformation oft die sterische, also die Van-der-Waals-Abstoßung reduziert. Ein gutes Beispiel hierfür ist eine Studie über die Stereoselektivität in Ringöffnungsreaktionen von Oxetan, die von chiralen Phosphorsäuren katalysiert werden. Abbildung 12 zeigt die untersuchte Reaktion. Hier vermittelt der Katalysator 2 a die Öffnung von 1 a (R′=Ph), und in der Folge wird 3 a mit 94 % ee gebildet.41
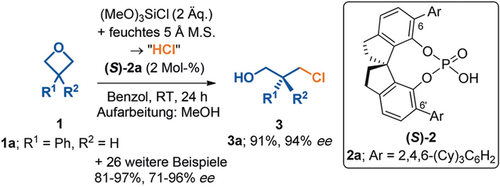
Stereoselektive Oxetan-Ringöffnung katalysiert von einer chiralen Phosphorsäure.
Die Übergangszustände, die zu dem Haupt- und Nebenprodukt führen, sind in der Abbildung 13 dargestellt. Auf der rechten Seite ist eine Überlagerung des optimierten Katalysators mit den beiden Übergangszuständen der katalysierten Reaktionen gezeigt. Der ungünstigere Übergangszustand zeigt erhebliche Deformation von der relaxierten ÜZ-Geometrie und ist ursächlich für dessen höhere Energie. Eine ähnliche Analyse führt zum Verständnis der Stereoselektivität in Nazarov-Cyclisierungen mit dem chiralen Thioharnstoffkatalysator von Tius.42
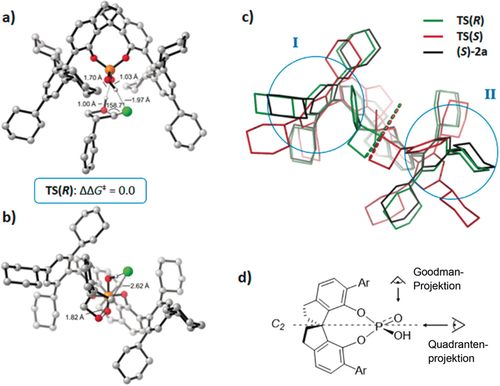
Übergangszustände für Oxetan-Ringöffnungen. Diese werden rechts überlappend mit der Katalysatorstruktur dargestellt.
4.9. Reaktivität und Regioselektivität von Arin-Additionen und Cycloadditionen
Die Gruppe um Garg konnte zeigen, dass die nukleophile Addition an Arinen, wie beispielsweise an den in Abbildung 14 dargestellten Indol-inen, in vielen Fällen mit einer hohen Regioselektivität abläuft. Das Distortion/Interaction- oder Activation-Strain-Modell hat sich im Verständnis und in der Vorhersage der Produkte für diese Reaktionen bewährt. Cheongs Arbeit führte zu einem Durchbruch auf diesem Forschungsgebiet,43a und es wurde demonstriert, wie das Modell sowohl Regioselektivitäten als auch Reaktivitäten korrekt vorhersagen kann.
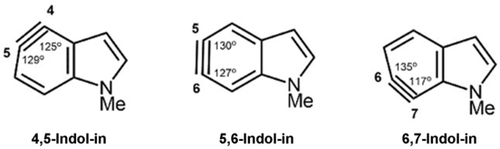
Strukturen von Indol-inen.
Die berechneten Innenwinkel des Ringsystems (Abbildung 15) zeigen, dass die Indol-ine eine Deformation aufwiesen. Ein nukleophiler Angriff an der lineareren Seite (größerer Innenwinkel) ist bevorzugt, weil wenig geometrische Verformung und Energieänderung zur Erreichung des ÜZ ausgehend vom Indol-in benötigt wird, wenn das Kohlenstoffatom mit einem Innenwinkel von 135° vom Nukleophil angegriffen wird. Zwei dieser Übergangszustände sind in Abbildung 15 dargestellt.
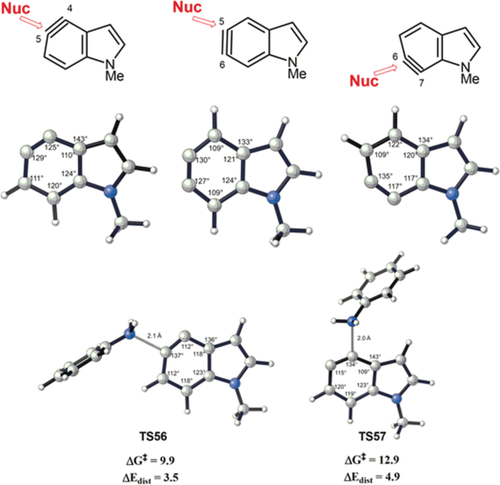
B3LYP/6-31G(d)-optimierte Strukturen von 4,5-Indol-inen, 5,6-Indol-inen, 6,7-Indol-inen und die Übergangszustände (TS56 und TS57) für die Anilin-Addition an 4,5-Indol-in.
Die berechneten Deformationsenergien für TS56 und TS57 betragen 3.5 kcal mol−1 bzw. 4.9 kcal mol−1. Die relative Reaktivität wird von diesen Deformationsenergien bestimmt. Das D/I-Modell sagt auch die Regioselektivität in anderen experimentell untersuchten Beispielen korrekt voraus.43a–43f Die linearere Seite des Arins zeigt auch experimentell eine Präferenz für den nukleophilen Angriff. Große Unterschiede in den Innenwinkeln des Rings führen zu hohen Regioselektivitäten.
Bei Einführung einer induktiv ziehenden I-Methoxygruppe an C3 in 3-Methoxydidehydrobenzol oder 3-Methoxycyclohexin werden das Arin oder Alkin erheblich deformiert (Abbildung 16). Die Bent-Regel43g besagt, dass diese C3-Methoxygruppe eine Rehybridisierung des C2-Atoms bewirkt. Durch die größere Linearität der Alkingruppe an C1 des 3-Alkoxycycloalkins findet hier bevorzugt der nukleophile Angriff statt. In einer ähnlichen Analyse wurden die Regioselektivitäten bei der nukleophilen Addition an 3,4-Pyrid-inen und Piperid-inen erklärt.43h
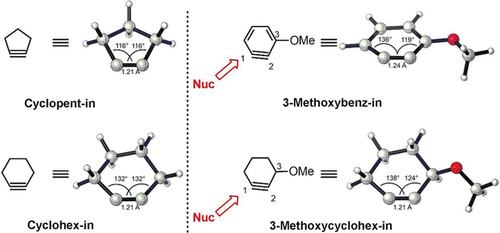
Optimierte Strukturen von 3-Methoxydidehydrobenzol und 3-Methoxycyclohexin, berechnet mit M06-2X/6-311+G(2d,p) und PCM (THF). Positionen der nukleophilen Angriffe werden angezeigt.
5. Weitere Aspekte
5.1. Vergleich zur Marcus-Theorie
Die Marcus-Theorie des Elektronentransfers verknüpft die Aktivierungsenergie einer Reaktion mit den thermodynamischen Parametern des Systems.24 Die potentielle Energie der Deformation eines Systems entlang der Schwingungsreaktionskoordinate (Abbildung 17) wird mit zwei Parabelkurven dargestellt, eine für die Deformation der Reaktanten entlang der Reaktionskoordinate und eine zweite für die Deformation der Produkte entlang der gleichen Koordinate. Die Reorganisationsenergie λ ist als die Energie definiert, die benötigt wird, die Kernkonfiguration der Reaktanten in die der Produkte zu deformieren, ohne einen Elektronentransfer zuzulassen, oder, allgemein gesprochen, ohne die Relaxation der elektronischen Zustände zuzulassen.
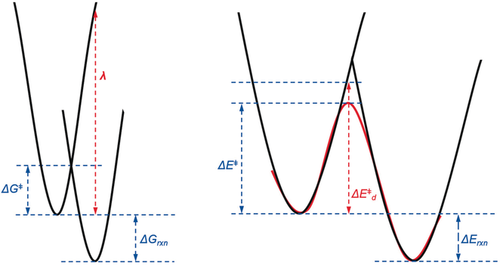
Energieterme in der Marcus-Theorie (links) und im Distortion/Interaction-Modell (rechts).
Dagegen ist die Deformationsenergie in unserem Distortion/Interaction- oder Activation-Strain-Modell als die Energie definiert, die benötigt wird, die Reaktanten in die Geometrie zu überführen, die sie in den Übergangszuständen aufweisen (Abbildung 17, rechts). Die Gestalt der Potentialkurve für die Reaktion kann in erster Näherung aus dem Überlapp der in der Marcus-Theorie verwendeten Parabelkurven erhalten werden.
Obwohl diese beiden Modelle recht unterschiedlich sind, liegt ihnen beiden die Annahme zugrunde, dass die Reaktivität stets mit einer Kombination von Thermodynamik (die sich in ΔGrxn und ΔErxn niederschlägt und die Position des Übergangzustandes beeinflusst) und den Energien, die benötigt werden, um die Reaktanten in Richtung der Produkte zu deformieren, erklärt werden kann. Die Reorganisationsenergie ist die Energie, die benötigt wird, um die Reaktanten in Richtung der Produkte zu deformieren, ohne eine Relaxation der elektronischen Zustände zuzulassen.
5.2. Solvatationseffekte
und die Wechselwirkung 
der Reaktanten im solvatisierten Zustand berechnet werden.44 Die Gleichung (3) wird dann entsprechend abgeändert, und ΔEsol(ζ) repräsentiert das Reaktionsprofil in Lösung [Gl. 7].
(7)Tatsächlich wurde dieser Ansatz bereits im Abschnitt 4.1 über die E2-/SN2-Reaktivität verfolgt. Dort wurde besprochen, wie die Solvatation des Reaktionssystems X−+CH3CH2Y die Base/das Nukleophil X− (genauer: dessen HOMO) stabilisiert und damit die Wechselwirkungskurve weniger stabilisierend wird.18b Dadurch hat die Reaktionsspannung einen größeren Einfluss auf den Gesamttrend der Reaktionsbarriere, und damit wird der weniger deformierte SN2-Reaktionspfad bevorzugt (siehe Abbildung 3). Ähnliche Effekte finden sich auch für andere organische und metallorganische Reaktionen, wie die metallvermittelte Bindungsaktivierung, die entweder über eine direkte oxidative Insertion oder über eine nukleophile Substitution verlaufen kann.44
Ein interessantes Beispiel findet sich in unserer Studie über die Palladium-katalysierte C-X-Bindungsaktivierung von Halogenmethanen.44 Dieser Prozess kann über zwei stereochemisch unterschiedliche Reaktionspfade verlaufen (Schema 3): (i) über die direkte oxidative Insertion (OxIn), welche unter Retention der Konfiguration am C verläuft; und (ii) über eine SN2-Substitution, welche eine Inversion der Konfiguration am C bedingt. Ein assistierendes Anion, welches wir durch die Modifikation des Pd-Katalysator zu PdCl− simuliert haben, und Solvatation, die mit COSMO simuliert wurde, beeinflussen die Gesamtreaktivität und die Selektivität zwischen den OxIn- und SN2-Reaktionspfaden. Der SN2-Reaktionspfad ist inhärent mit einem höheren Grad an Deformation des Substrates im ÜZ verbunden, was zu einer höheren Aktivierungsspannung 
und einer höheren Reaktionsbarriere ΔE≠ im Vergleich zur OxIn-Reaktion führt.
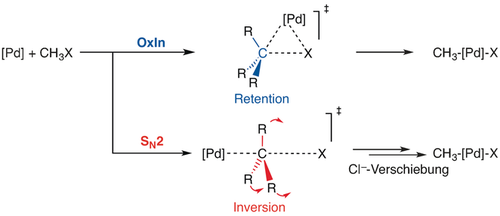
Oxidative Addition über direkte oxidative Insertion (OxIn) oder über eine nukleophile Substitution (SN2).
Dieser Befund kann nun mithilfe der ÜZ-Wechselwirkungsenergie 
manipuliert werden.44 Diese bevorzugt den SN2-Reaktionspfad, da das stärker deformierte Substrat auch einen besseren Partner für elektrostatische und Donor-Akzeptor-Orbital-Wechselwirkungen darstellt. Oder anders ausgedrückt: Immer wenn die ÜZ-Wechselwirkungsenergie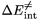 
klein ist, wird der Selektivitätstrend von der Aktivierungsspannung 
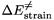bestimmt (und umgekehrt). Bemerkenswert sind die Parallelen in der Konkurrenz zwischen OxIn und SN2 (Schema 3) sowie E2 und SN2 (Abbildung 3). Der einzige Unterschied ist, dass hier die SN2-Reaktion über den stärker deformierten Reaktionspfad verläuft, d. h. benachteiligt wird, wenn die Reaktionsspannung dominiert, und bevorzugt verläuft, wenn die Wechselwirkung groß ist. Sie verhält sich also genau so wie E2 in Abbildung 3. Entsprechend übernimmt die OxIn hier die Rolle, die die SN2-Reaktion in Abbildung 3 spielt. Aus diesem Grund bevorzugt die Anion-assistierte Reaktion den SN2-Reaktionspfad, da sie das Bindungsvermögen des Modellkatalysators erhöht. Solvatation, zusätzlich zur Anionen-Assistenz, führt hingegen dazu, dass die Bindungsfähigkeit vermindert wird und wieder der OxIn-Reaktionspfad bevorzugt wird.
(8)
(9)Bemerkenswert ist, dass ΔEsolute(ζ) oft (aber nicht notwendigerweise) dem PES der Gasphasenreaktion sehr ähnlich ist. Die Terme ΔEstrain(ζ) und ΔEint(ζ) beziehen sich auf die Deformation und auf die gemeinsamen Wechselwirkungen zwischen den gelösten Reaktanten in einer Geometrie, die sie im gelösten Zustand aufweisen, jedoch ohne die explizite Anwesenheit des Lösungsmittels (Abbildung 18). Damit wird die Reaktionsspannung als Energiedifferenz zwischen dem gelösten Reaktionssystem relativ zu den Reaktanten (in Lösungsgeometrie) im Vakuum berechnet. Die Solvatationsenergie ΔEsolvation(ζ) berücksichtigt sowohl die Wechselwirkung der gelösten Stoffe mit dem Lösungsmittel als auch die Wechselwirkung mit Lösungsmittelkavitationen, d. h. die Bildung von Hohlräumen innerhalb des Lösungsmittels durch die Anwesenheit des gelösten Stoffes.
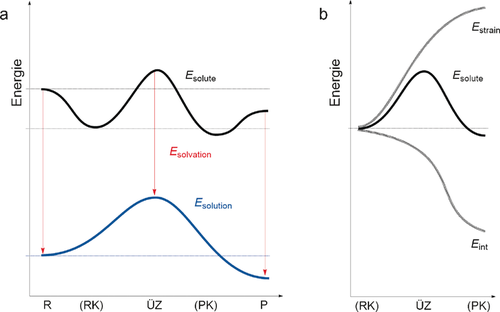
Activation-Strain-Modell für die Reaktionen in Lösung mit der gelösten Stoff-Lösungsmittel-Wechselwirkung: a) Die PES des gelösten Stoffes im Vakuum, ΔEsolute, plus die Solvatationswechselwirkung zwischen gelösten Stoff und Lösungsmittel, ΔEsolvation, ergeben zusammen die PES in Lösung, ΔEsolution. b) Die PES des gelösten Stoffes im Vakuum wird anhand einer Zerlegung in Deformation und Wechselwirkung analysiert.
Dieser Ansatz ermöglicht es, die normale Activation-Strain-Analyse der gelösten Stoffe um den Effekt der Solvatationswechselwirkung zu erweitern. Die Analyse sowohl von SN2-Substitutionen an verschiedenen elektrophilen Zentren (z. B. SN2@C, SN2@Si und SN2@P) als auch die Untersuchung von Rückseiten- und Vorderseitenangriff in Ionenpaar-SN2-Reaktionen zeigen, wie die Solvatation in den meisten Fällen zu einem Anstieg von Reaktionsbarrieren führt. Die Rolle von Reaktanten- und Produktkomplexen, die in der Gasphase eine dominierende Stellung einnehmen, wird gemindert.45 Dies ist auf die unterschiedliche Solvatation zurückzuführen, die stärker die Reaktanten und Produkte stabilisiert als die entsprechenden Reaktionskomplexe und den ÜZ im Besonderen (Abbildung 18 a).
5.3. Anwendungen auf Unimolekulare Reaktionen
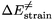. Ein aufschlussreicherer Ansatz ist es, zwei Fragmente im Reaktanten zu identifizieren, die eine klar definierte relative Bewegung zueinander ausführen. Ein solches Beispiel findet sich für 1,2-dyotrope Reaktionen vom Typ I, die in Gl. 10 gezeigt werden (E=C und Si; X=H, CH3, SiH3, F bis I).46
(10)Wie von Fernandez et al. bemerkt wurde,46a kann diese Reaktion, als die Umwandlung zwischen zwei (sehr stark gebundenen!) Reaktionskomplexen X2+ER2=CR′2 aufgefasst werden. Tatsächlich ähnelt dieser Prozess sehr stark einer Rotation des [X - - - X]-Fragmentes (oder “Reaktanten”) relativ zum H2E=CH2-Fragment (oder “Reaktanten”), siehe Diagramm A.
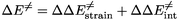(11)Aus dieser Analyse ergibt sich, dass eine schwächere C-X-Bindung im ÜZ die Ursache für die Reaktionsbarriere ist. Folglich können Reaktivitätstrends in der Variation von X leicht mit der Deformierung der C-X-Bindung zur Geometrie des ÜZs erklärt werden. Die Barriere verringert sich beispielsweise systematisch, wenn die C-X-Bindung entlang C-F, C-Cl, C-Br und C-I schwächer wird.46a
Gemeinsam mit Fernandez und Cossío47 haben wir Reaktionstrends in der thermischen Cycloisomerisierung von 1,3-Hexadien-5-inen, A=B−C=D−E≡F untersucht und analysiert. Diese Reaktion verläuft über die Bildung einer gebogenen Allen-Zwischenstufe mit relativ hoher Aktivierungsbarriere, gefolgt von einer schnellen 1,2-H-Verschiebung und dann zur Bildung des sechsgliedrigen aromatischen Rings. Die Aktivierungsspannungsanalyse zeigt, dass der kontrollierende Hauptfaktor dieser Hopf-Cyclisierung mit der geometrischen Deformationsenergie der Rotation der endständigen Gruppe [A] um die Doppelbindung verbunden ist. Diese Rotation ist für das Erreichen einer günstigen HOMO-LUMO-Überlappung mit der Alkinfunktionalität [F] zur Bildung der neuen A-F-Einfachbindung notwendig.
Das Distortion/Interaction- oder Activation-Strain-Modell kann auch auf intramolekulare Reaktionen mit einem Fragmentierungsschema angewendet werden (Abbildung 19).48 Hier haben wir zunächst die Deformations- und die Wechselwirkungsenergien der miteinander reagierenden Komponenten berechnet und gesondert davon die Deformationsenergie der Verbrückung, die die beiden Fragmente zusammenhält. In Abbildung 19 repräsentiert die durchgezogene schwarze Linie links die Potentialfläche einer intramolekularen Cycloaddition. Die reaktiven Komponenten des Substrates sind blau dargestellt, während die Verbrückung, die die reaktiven Komponenten zusammenhält und die Reaktion zu einer unimolekularen Reaktion macht, orange eingefärbt ist. Praktisch werden die reaktiven Komponenten in Grundzustandsstrukturen überführt und separiert. Wasserstoffatome werden an die Atome addiert, an denen die kovalenten Bindungen gebrochen wurden (Abbildung 19, rechts unten). Die Einzelpunktenergien für die wechselwirkenden reaktiven Komponenten im Übergangszustand (Abbildung 19, rechts Mitte) und die separierten reaktiven Komponenten in ihrer Übergangszustandsgeometrie (Abbildung 19, rechts oben) werden ebenfalls berechnet. Die Summe der gesamten Deformations- (
) und Wechselwirkungsenergie 
) ergibt die ersichtliche Aktivierungsenergie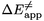 
. Die Differenz zwischen
und 
ist die Deformationsenergie der Verbrückung 
. Diesem Ansatz liegt die Annahme zugrunde, dass sich die Deformation der Verbrückung und die Deformation der reagierenden Komponenten additiv verhalten. Mit diesem Fragmentierungsschema können intramolekulare Reaktionen mit dem D/I-Modell untersucht werden.48
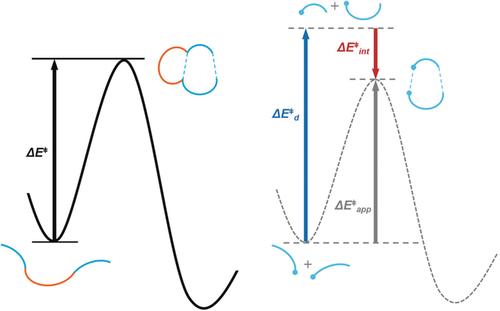
Links: Energiediagramm für eine intramolekulare Reaktion. Rechts: Distortion/Interaction-Modell für eine intramolekulare Reaktion unter Wegnahme der Verbrückung.
6. Schlussfolgerung
Die hier besprochenen Anwendungen zeugen von der breiten und allgemeinen Einsetzbarkeit unseres Modells bei unimolekularen und bimolekularen chemischen Reaktionen. Es baut auf Roald Hoffmanns1 qualitativen störungstheoretische Modellen auf, welche sich als so nützlich für die Erklärung vieler Phänomene in der Chemie erwiesen haben und folgt dem gleichen Geiste. Auch mit den weiteren Entwicklungen und Anwendungen, wie den durch Walsh und anderen49 eingeführten Orbital-Korrelationsdiagrammen ist es artverwandt. Die Konzepte von Deformation und Wechselwirkung sind universell gültig und damit auf alle Disziplinen der molekularen Wissenschaften anwendbar. Sie bilden einen vereinheitlichten Ansatz, der die Gemeinsamkeiten zwischen scheinbar nichtverwandten chemischen Phänomenen enthüllt und die gemeinsamen physikalischen Mechanismen aufdeckt.
Ferner ist unser Modell per Definition exakt, d. h. so genau wie die in den Berechnungen benutzte quantenchemische Methode. Dieses Modell trägt allen Faktoren Rechnung (Deformation, Reaktionsspannung und Wechselwirkung), die für die Berechnung der Aktivierungsenergie benötigt werden. Deswegen kann unser Modell sowohl zur Erforschung der Haupttrends als auch zur Analyse von subtilen Effekten eingesetzt werden; in den Worten von Woodward und Hoffmann:5d “Ausnahmen gibt es nicht!”
Das Modell ist nicht nur universell und exakt, es stellt vor allem auch einen kausalen Zusammenhang zwischen (beobachteten oder berechneten) Reaktivitätstrends und den zugrundeliegenden physikalischen Faktoren her, die ihren Ursprung in der molekularen und elektronischen Struktur der Reaktanten haben. So hängt die Deformation oder Aktivierungsspannung von der Starrheit der Reaktanten, der Stärke der zu brechenden Bindung und vom Charakter des bestimmten Reaktionsmechanismus ab, das heißt, vom Ausmaß, mit dem sich die Reaktanten entlang des Reaktionspfads geometrisch verformen müssen. Ebenso hängt die Wechselwirkung zwischen den Reaktanten von ihrer räumlichen Form und ihrer elektronischen Struktur (Orbitale oder VB) ab. Dies stellt wirkungsvolle Hilfsmittel für das rationale Design chemischer Reaktionen zur Verfügung.
Professor Roald Hoffmann zum 80. Geburtstag gewidmet
Acknowledgements
Wir danken der Niederländischen Organisation für Wissenschaftliche Forschung (NWO) und der U.S. National Science Foundation (NSF CHE-1361104) für die finanzielle Unterstützung dieser Forschung. Wir danken Dr. Fang Liu und Dr. Trevor A. Hamlin für Diskussionen und Hilfe bei der Herstellung von Abbildungen. Dr. Lando P. Wolters danken wir für die Gestaltung des Titelbildes und Deckblattes. Dr. Jörn Nitsch half bei der Übersetzung ins Deutsche.
Conflict of interest
Die Autoren erklären, dass keine Interessenkonflikte vorliegen.
Biographical Information
F. Matthias Bickelhaupt promovierte an der Universität Amsterdam unter Anleitung von N. M. M. Nibbering und E. J. Baerends im Jahre 1993. Anschließend arbeitete er für P. von R. Schleyer, T. Ziegler und R. Hoffmann, begann als Professor in Marburg und erhielt 1999 eine permanente Anstellung in Amsterdam. Zurzeit ist er Professor für Theoretische Chemie an der Vrije Universiteit Amsterdam und an der Radboud Universiteit Nijmegen. Er ist Mitglied der Koninklijke Hollandsche Maatschappij der Wetenschappen. 2002 wurde er mit dem VICI-Preis der Nederlandse Organisatie voor Wetenschappelijk Onderzoek ausgezeichnet.
Biographical Information
Kendall N. Houk promovierte in Harvard mit experimentellen Arbeiten über pericyclische Reaktionen (bei R. B. Woodward, 1968), wandelte sich während seiner Laufbahn aber zum theoretisch arbeitenden Chemiker. Nach Professuren an der Louisiana State University und der University of Pittsburgh wurde er Saul Winstein Chair in Organic Chemistry an der University of California Los Angeles (UCLA). Er ist Fellow of the American Academy of Arts and Sciences sowie Mitglied der US National Academy of Sciences und der International Academy of Quantum Molecular Sciences. Die Universität Essen verlieh ihm 1999 die Ehrendoktorwürde.
