Biophysical Approach to Understand Life and Cancer
ABSTRACT
Background
From the perspective of biology, the characteristics of life can be categorized as cellular organizations, homeostasis, metabolism, growth, reproduction and heredity, response to stimuli and adaptation to the environment. From the perspective of physics, living organisms are highly ordered, complex, thermodynamically open systems; they are in non-equilibrium phase. According to the second law of thermodynamics, every system in the universe is going to the disorder spontaneously. Maximum entropy signifies a thermodynamic equilibrium which means the death. Today, cancer is a major global health problem and despite the explosive development of our knowledge about the carcinogenesis the “war on cancer” has not yet been won.
Aims
To examine life and cancer together based on current biophysical approach and to shed light on new paradigms.
Materials & Methods
A systematic literature search for publications on a thermodynamic approach to understand life and cancer was conducted in PubMed without language restrictions. The reference lists of identified studies were also used as additional knowledge.
Results
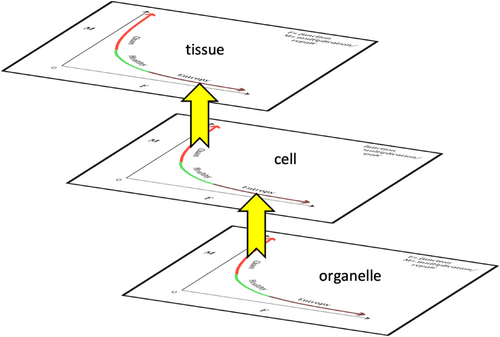
Living organisms exchange entropy and they gain information from the external environment. Information can be stored as memory. Life is a category of emergence like art composed from correct modules. On the contrary, cancer is the emergence of a disease formed by incorrect modules. Cancer is a chaotic disease at least for a limited period and cannot arise from healthy functional tissue units. Chaos of the lower level may be associated with the entropy increase of upper level.
Conclusions
Biologic chaos control is possible.
1 Introduction
There is not a comprehensive definition of life. From the perspective of biology, which is the science that studies life, the characteristics of life can be categorized as cellular organizations, homeostasis, metabolism, growth, reproduction and heredity, response to stimuli, and adaptation to the environment. From a physics perspective, living beings are thermodynamic systems with an organized molecular structure that can reproduce itself. The basic units of life are cells.
Cancer is a major global health problem despite the explosive development of our knowledge about the molecular mechanisms of carcinogenesis [1-4]. Today, the “war on cancer” has not yet been won; cancer is far more easily prevented than cured [5-7]. Therefore, we clearly need more efforts to conquer cancer. The aim of this review is to scrutinize life and cancer together and shed light on new paradigms.
In this review, we will try to give some enlightened concepts, such as entropy, information, emergence, and chaos related to life and cancer, as well as the role of chaos control in cancer treatment.
2 Entropy
Life is governed by energy; it is conserved according to the first law of thermodynamics and, according to the second law, it is dissipated irreversibly as heat, and every system in the universe is going to disorder (or more accurately, disorganization) spontaneously [8-15]. The second law relates only to the initial and final situations of systems, not the dynamics of the system [12]. We can give many examples of entropy in ordinary life; for example, a hot cup of coffee will get cold within minutes, an unplugged hot iron cools, a candle melts, or the air leaks from a puncture of a tire. All of these events are spontaneous and irreversible. Heat is transferred spontaneously from a hot to a cold body. Time's arrow is unidirectional in spontaneous processes. The positive time direction is associated with the increase of entropy [10]. Inverse situations are possible only by work and energy. Energy must be used to produce a highly ordered state [13]. The term entropy was introduced in 1865 by Rudolf Clausius, and in the early 1870s, Ludwig Boltzmann realized the entropy formula, which is S = k log W [9]. The symbol W in this formula derived from a German word “Wahrscheinlichkeit” for probability [9]. Entropy increases with temperature, and it is a measure of how many states are accessible at a given temperature. The symbol k here is the Boltzmann constant (1.3806488 × 10−23 J/K). We can see this fundamental formula on Boltzmann's gravestone in Vienna. A crystalline solid material is in a highly ordered and low-entropy state. Transition from one state to another is associated with the increase of entropy (Figure 1) [14, 15]. Gas form of a material is in a high disorder and maximum entropy state. In the low-entropy situation, energy is concentrated in atomic bonds; in the maximum-entropy situation, energy is spread out in atomic bonds. Maximum entropy signifies a thermodynamic equilibrium, which means death [8]. Therefore, we can define death more easily than life physicochemically.
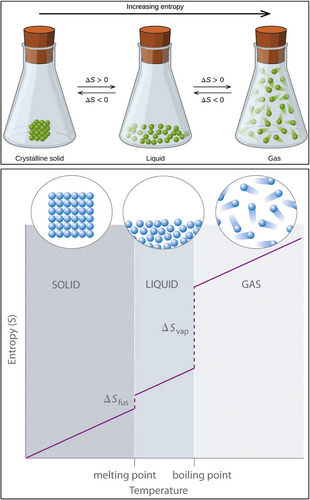
The universe itself is an isolated system, but inside the universe, there are two distinct systems: closed (isolated) and open [8]. The closed systems exchange neither energy nor matter. In these systems, energy is dissipated irreversibly as heat and entropy increase rapidly. The open systems exchange matter, energy, and entropy. Living organisms are open systems. They are highly ordered (complex) dynamic systems and are in the nonequilibrium phase. In open systems, the entropy increase is slow. The final state of both systems is thermodynamic equilibrium. Prigogine, who was named Nobel Laureate in Chemistry in 1977 for his contributions to nonequilibrium thermodynamics, defined living organisms as dissipative structures [10]. They are structured organizations. Living systems defy entropy. Life is an extraordinary challenge against entropy.
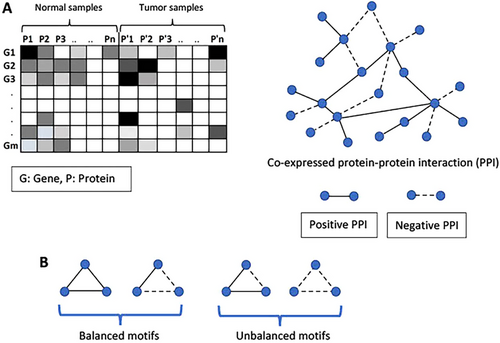
Somatic, differentiated human cells are mortal; they undergo the Hayflick limit, after a certain number of cell divisions, proliferation stops, and subsequently, cells senesce and die [16-18]. American anatomist Hayflick demonstrated that normal human fetal cell population will divide between 40 and 60 times in cell culture before entering a senescence phase [16]. Cellular senescence and programed cell death are protective mechanisms for maintaining tissue homeostasis to remove diseased, dysfunctional, or unnecessary cells [4]. All living things experience an increase in entropy [19]. Entropy is a measurable quantity connected with complexity, and it is usable to quantify the level of disorder associated with a dynamical process that has a number of sites [20]. The cellular phenotype is a result of a complex network of molecular interactions [21]. The integration of gene expression data with protein interaction networks (PINs) permits the development of a network-based framework at the systems level, and Cheng et al. demonstrated that tumorigenesis could be characterized by a significant increase of gene network entropy in the eight cancer types they studied from large-scale RNA-Seq data generated in The Cancer Genome Atlas (TCGA) project versus normal tissues [22]. They also found that the ratio of unbalanced motifs in tumors is higher than that of normal tissues. Figure 2 shows simple diagrams of co-expressed protein–protein interaction (PPI) network and motifs (balanced and unbalanced) of gene–gene interactions.
In cellular senescence and mammalian organismal aging, increased entropy manifests itself as a loss of epigenetic and genetic information [19]. Although there is an increase in entropy in two degenerative processes in life (aging and cancer), the main difference is concentrated on telomeres. Organismal aging is a time-dependent deterioration of function and physiology [23]. Accumulation of DNA damage with age affects the genome, and particularly telomeres are susceptible to age-related deterioration [24]. Telomere attrition and shortening explain the limited proliferative capacity of normal cells, and this replicative cellular senescence is accepted as a hallmark of aging [25]. On the contrary, enabling replicative immortality due to the activation of telomerase (the specialized DNA polymerase that adds telomere hexanucleotide repeat segments to the ends of telomeric DNA) is one of the hallmarks of cancer [3]. The limited number of successive replication in normal cells is associated with two distinct barriers to proliferation: senescence and crisis [3]. In the crisis phase, the majority of cells in the population die, but rarely do some cells emerge from this population and exhibit unlimited replicative potential by upregulating the expression of telomerase [3]. In Section 6, we will discuss critical points, transition to chaotic behavior, and the emergence of a new system in complex systems.
3 Information
Dissipative structures (living organisms) exchange entropy, and during this exchange, they gain information from the external environment. Entropy is oppositely linked to the amount of information [8, 12]. Information is imported from the external environment and can be stored as memory [8]. Memory is the capacity of the organisms to benefit from their past experiences [26]. Information should be coded. Shannon published an information theory in 1948 [27]. He investigated the measuring and processing information, and he used the term bit (binary digit) (0 = off, 1 = on) for the first time [27]. John von Neumann quantized this using the term quantum bit (qubit) (0, 1, and 0 and 1 at the same time due to superposition) [12, 28]. Neumann says that “all life can be expressed as the flow of information” [29]. This is the principle of artificial life today. The flow of information from one subsystem to another permits the self-organization of the system.
In physics, a system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole [30]. To be able to talk about entropy, we must have more than one particle; therefore, we can only talk about the entropy of a system. A fully functioning open complex system has some important characteristics, such as relationships, communication, self-organization, self-adaptation, and the potential to create a new emergence [31]. Internal relationships within a system produce self-organization; external relationships provide self-adaptation [31]. These features can be identified within a healthy organism, which is a robust open system. The orderly complexity, versatility, and robustness of living systems are the main issues of contemporary cell biology [32]. Order preservation (or order stability) is one of the basic features of functional biological systems; to be stable, a biosystem should be able to control entropy [33, 34]. Dynamical systems may be linear or nonlinear. Living systems are nonlinear, dynamic, and complex [32, 35, 36].
Information can be descriptive (semantic) or prescriptive (instructive) [11]. Both of these organizations are abstract, conceptual, and nonphysical entities [37]. Prescriptive information refers to linear digital instructions using a symbol system such as 0 and 1 or A, G, T, and C from a phase space of four nucleotides [37]. Prescriptive information provides cybernetic controls.
Life is not possible without matter, energy, and information [34, 38]. Biology without information is a matter of philosophical debate; this is not the subject of this review [39]. We can say that main difference between a living organism and inanimate material may be the materialization of information (MI) in the living world [11, 40, 41]. Prescriptive information may be turned into symbolic one through materialization into the form of the base sequence of genomes [11, 37]. The information carried by the linear sequence of nucleotides from a gene was proposed by Watson and Crick in 1953, and a few years later, the mechanism of protein synthesis was discovered, the transfer of linear information from genes to proteins was found, and the discovery of the structure of DNA transformed biology profoundly [42-44]. DNA has two types of digital information: the genes that encode proteins, which are the molecular machines of life, and the gene regulatory networks that specify the behavior of the genes [44]. The “cellular machinery” and “information stored in the genome and epigenome” may be thought of as biological hardware and software, respectively [19]. Another analogy can be made also between MI and three-dimensional (3-D) or even 4-D printing at nanoscale during translation [45]. Figure 3 shows a schematic diagram of the MI during coding by base sequences and protein synthesis by amino acids. Molecules may also have different information in previous steps. Lehn demonstrated that molecules could recognize each other with structure-specific interactions of high selectivity [46]. Proteins are complex biological macromolecules; they are involved in almost every biological process. After translation on ribosomes, linear protein chains must generally fold into 3-D structures to gain functional activity [47]. The amino acid sequence, encoded in the DNA, contains all necessary information for the specific 3-D structure of a protein. Besides this, a specific class of proteins (molecular chaperones) assists in de novo folding and refolding of stress-denatured proteins [47]. Intracellular protein homeostasis (or proteostasis) is crucial for cellular and organismal health. This is achieved by either molecular chaperones and their regulators or ubiquitin–proteasome system (UPS) and autophagy–lysosomal system. UPS and the autophagy system mediate the timely removal of irreversibly misfolded and aggregated proteins. Constant chaperone surveillance is necessary for protein homeostasis. Members of the chaperone protein family are known as stress proteins or heat-shock proteins (HSPs). Impaired proteostasis (chronic expression of unfolded, misfolded, or aggregated proteins) is linked to aging and some aging-related pathologies, such as Alzheimer's disease, Parkinson's disease, and cataracts [25, 48]. After translation and protein folding, posttranslational modifications of proteins have an important role in protein trafficking [49]. One of the pioneer researchers of this area, Blobel, discovered that proteins have intrinsic signals that govern their transport and localization in the cell [50]. Protein tagging affects the function, structure, location, and/or turnover of numerous intracellular proteins [51]. A well-known example of protein tags is KDEL (lysine, aspartic acid, glutamic acid, leucine) amino acid sequence. It is located on the C-terminal end of the amino acid structure of a protein. KDEL receptor in the Golgi complex is a key regulator of cargo protein traffic from the endoplasmic reticulum (Figure 3) [52]. The regulation of the many secretory pathways involved in the homeostasis of the signaling system remains to be determined.
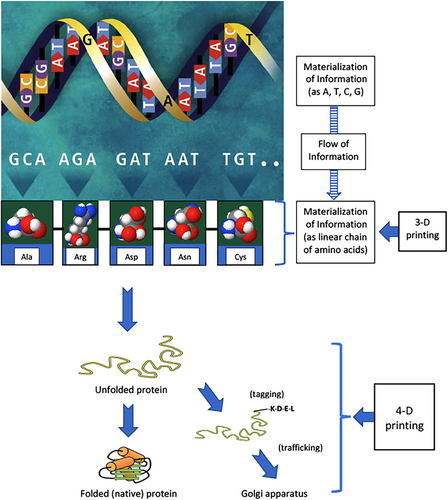
The cell's genome, transcriptome, proteome, and metabolome are distinct levels of organization of information [32]. Long-term information is stored in the genome, and the proteome is crucial for short-term information storage [32]. The transcription factor-controlled information is influenced by the metabolome.
4 Beginning of Life
At this point, we are facing a contradictory situation: There is entropy or disorder on the one hand and highly ordered living organisms on the other. How can we explain this well-known paradox? How did life begin on earth, despite the second law of thermodynamics? One century ago, German physiologist Loeb proposed that “we must either succeed in producing living matter artificially, or we must find the reasons why this is impossible” [53, 54]. Until the mid-19th century, “spontaneous generation,” which is the theory that held that living organisms could arise from inanimate matter, was widely accepted, but after van Leeuwenhoek and Pasteur's experiments on microorganisms, this theory has been shown to be incorrect. Virchow's famous quote “omnis cellula e cellula” (any cell is derived from another cell) was considered to be the hallmark of cell theory [54]. And then attention turned to the origin of life, as all life seems to have evolved from a single form (the first cell, protocell) and the last universal common ancestor (LUCA) of modern organisms around 4 billion years (by) ago. In the 1950s, Miller and Urey performed a chemical experiment to test this abiogenesis hypothesis (the transition from nonliving organic compounds to living entities) that simulated the conditions to be present on the early, prebiotic Earth and tested the chemical origin of life under those conditions [55]. This experiment was based on Oparin's and Haldane's hypothesis (in 1924 and 1929, respectively) that putative conditions on the primitive Earth favored chemical reactions that synthesized more complex organic compounds from simpler inorganic precursors [56-58]. They attempted to brew a “primordial soup” by mixing basic chemicals, such as water, methane, carbon dioxide, ammonia, oxygen, and hydrogen, under heat, light, and electricity and found traces of amino acids and trace amounts of simplest sugars. Subsequent variations of the Miller experiment produced the chemical building blocks of RNA and DNA [59]. At Harvard, biochemist Szostak, who has spent over two decades trying to understand the origin of genes, believes that protocells emerged out of this primordial soup through random meeting between micelles (lipid vesicles) and chains of RNA [60]. This concept of protocell structure has both original simplicity and future complexity. Replication of both protocell and its encapsulated genetic material ultimately may give rise to modern cellular life under natural selection. Today, there is a discipline of synthetic biology; many research groups are involved in the construction of artificial cells, and a team from the J. Craig Venter Institute published an article in July 2010 entitled “Creation of a bacterial cell controlled by a chemically synthesized genome” [61]. Actually, this was not producing living material artificially; this was synthetic genome transplantation to a bacterial cell. We are still far from answering Loeb's proposition.
To answer the question about the beginning of life on Earth, we should look at the history of the universe. According to cosmologic, astrobiological, and paleontological data, the origin of life on earth should be 3.7 by ago [62, 63]. The age of oldest prokaryotic fossils is 3.5 by, eukaryotics 2 by, and multicellular eukaryotes 600 million years. Free oxygen production to the atmosphere by first photosynthesis from cyanobacteria, which was crucially important for life approximately 2.5 by ago. All living organisms are fuelled directly by photosynthesis or indirectly by high-energy nutrition [62]. In the solar system, life is possible only in the habitable zone, which means not too cold, not too hot, just the right position in the universe. Another powerful force for life is evolution, because it supports the adaptation of living organisms to the environment [63].
Cells are thermodynamically open systems, and they have external relationships and communication with their environment. These interactions play an important role in the self-adaptation of complex systems such as living cells. During the exchange of matter, energy, and entropy, information is imported from the external environment [8]. Here, epigenetics constitutes a reversible middle- to long-term memory; environmental information is stored and used to improve adaptation to the environment [8]. We previously mentioned that the loss of epigenetic information is a hallmark of aging [19].
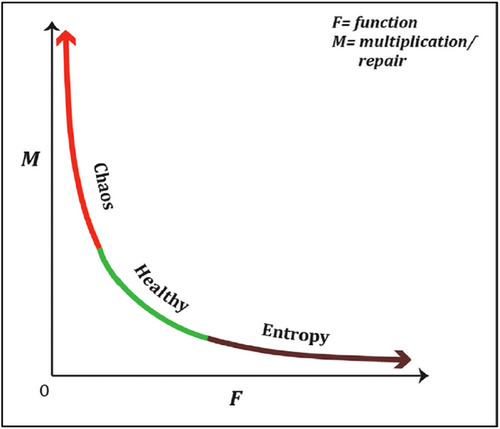
A living individual multicellular organism consists of hierarchical biologic levels from top to bottom: systems, organs, tissues, and cells [36, 64]. As Sigston and Williams illustrated with a very nice graphic, the living cells in a functional tissue unit (FTU) constitute a meta-stable system [35]. An FTU is a dynamic system that has the adaptability potential between inputs and outputs in response to internal and environmental changes to maintain its functional capability. There is an inverse relationship between function (F) and multiplication (M) in this unit (Figure 4) [35]. In the optimum healthy state, there is maximum adaptability with the environment, and there are periodic oscillations between an input and an output in many physiological events, such as cell cycle, metabolism, cardiac, muscle, and brain functions. Different stimulations may alter the optimum healthy state, for example, cellular proliferation (M) increases in wound healing; on the contrary, proliferation decreases in functional highly differentiated cells such as neurons. We will discuss the extreme levels of this diagram in Section 6. Human organism can be accepted as a multi-oscillator [65].
5 Emergence and Modularity
Emergence means occurrence. It is a central concept in philosophy, systems theory, complex systems, science, and art. It is the signature of complex systems [66]. We can define it as follows: The combination of some precursors as a whole produces a new formation that is different from its precursors. The expression that the whole is greater than the sum of its parts is attributed to Aristotle, and it is a non-reductionistic dictum that defines emergence [66]. A beautiful picture produced from oil paint and the painter's brush strokes is an example of the emergence. Music also emerges when you play the correct notes. German scientist Lüttge says “genes and genomes can be compared to a grand piano; music emerges when it is played” [67]. François Jacob, André Lwoff, and Jacques Monod discovered some control mechanisms of the genes: the operator genes, which control the structural genes [68]. Controlling the activity of the genes by specific nuclear proteins can be compared to the conductors of the symphony of life. What about incorrect notes? They produce only noise. We will discuss them in Sections 6 and 8.
We can give some other examples of emergence. Monocular vision is 2-D; binoculary vision is 3-D; a third dimension is a new formation. Emerging behavior is a new phenomenon special to the level considered, and it results from interactions among the constituents of the level [36]. Systems biology is also based on the understanding that the whole is greater than the sum of the parts [69]. On a biological level, our bodies are made up of many networks that are integrated at and communicating on multiple scales [69]. Only organisms are alive, not the molecules [70]. As Baranger put it so well, walking capability is one of the best examples of emerging behavior for human body; anyone studying only a leg, only a trunk, or only a head never understands walking [36]. Jean-Paul Sartre, who was awarded but declined The Nobel Prize in Literature in 1964, says, “in love, one and one are one”; I think that this is one of the best definitions of emergence.
In chemistry, one of the best examples of emergence is the formation of water droplets [35]. The combination of an oxygen atom with two hydrogen atoms produces water molecules, and finally, a water drop emerges from water molecules. Similarly, a proton and an electron come together to form an atom of hydrogen. Combinations of lower level objects assemble to constitute a new level or higher level object [35]. Every higher level is characterized by a new property not possessed by the lower level constituents (precursors). There is a hierarchy among levels: The direction from lower levels to higher levels is emergence, and the opposite direction is submergence. Combinations require energy, and a bonding structure enables self-organization. An emerging behavior also has the effect of changing the structure or creating a new structure [36]. It is evident that life is a category of emergence [67].
Biological systems are self-organizing and self-maintaining. As a result of emergence, life consists of some levels or scales [36, 64]. The levels of biological organization can range from bottom to top as subatomic particles, atoms, molecules, organelles, cells, tissues, organs, and systems [64]. Every level is an emergent unique, unitary entity. All features of life comprise structural (morphologic) and functional (physiologic) components [67]. These components can be considered modules [67]. Life is modular and consists of the holistic integration of modules. Modularity is separation, and emergence is integration [67]. Our genes are also modular (split genes); these modular genes have evolutionary advantages [59]. Intracellular-specific interacting molecules (pathways) are also accepted as modules [71].
6 Chaos
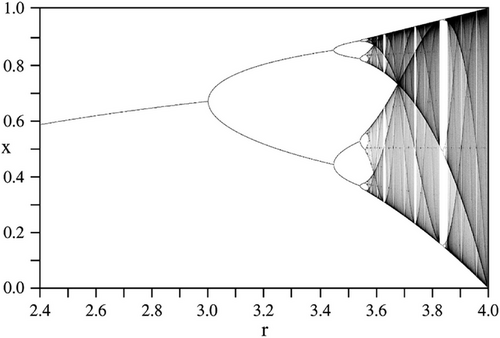
When we mention chaos, we should remember Lorenz's experiments. Edward Norton Lorenz (1917–2008) was an American mathematician and meteorologist at MIT. In 1961, he was simulating weather patterns on his computer. He wanted to see a sequence of data again, and to save time, he started the simulation in the middle of its course. The computer worked with six-digit precision, but he used rounded variables off to a three-digit number, so a value like 0.506127 was printed as 0.506. This difference was small, but he observed for the first time that very small errors of the calculations about atmospheric conditions result in big ends [72, 73]. This may be a storm or a hurricane. Very small, minuscule changes in the initial conditions can lead to highly diverse outcomes [74]. Any small uncertainty or error existing in the initial conditions will grow exponentially with time; it will become so large that we will lose all useful knowledge of the state of the system [36]. Lorenz discovered this sensitivity of chaotic systems to initial conditions, known as the butterfly effect [75]. Biological systems (or living systems) are essentially nonlinear, which means output is not proportional to input in these systems [74, 75]. One of the best examples of nonlinearity is the expansion of a balloon [76]. Progressive inflation of a balloon appears superficially to be linear; while the balloon is expanding, the changes are quite easy to predict, but at some point, the balloon will explode, and the output is a catastrophe, which is a nonlinear event that has not been predicted. As we mentioned previously, living systems consist of many physiological oscillations. Attractors are the elements of nonlinear dynamic systems. They are self-organized causal structures guiding the destiny of a dynamical system in the state-space [66]. Genes, proteins, and cells can be considered physiological oscillators [66]. The networks of genes, proteins, and populations of cells behave like coupled nonlinear oscillators [77]. Systems biology analyzes this network of networks (molecular, cellular, and organ networks) [69]. Oscillators are limit cycle attractors that have structural stability over time, like a pendulum swinging at regular intervals. A healthy cell phenotype corresponds to a stable attractor in state-space. For example, this may be the oscillation of a single protein or gene expression dynamics at the cellular level. Chaotic oscillations can arise in these biological oscillators [77]. Chaos or deterministic chaos, is the aperiodic, irregular, unpredictable, and unsynchronized (but sensitive to initial conditions) behavior of systems emerging under the influence of certain perturbations [75]. Chaos starts with a strange attractor (the locus of chaos); symmetry-breaking and bifurcation of the system follow this; it continues with new bifurcations and finalizes chaotic irregular oscillations (Figure 5) [75, 78]. These bifurcations are like a branching tree and are known as the Feigenbaum diagram [75]. The time delays in the oscillatory dynamics may give birth to chaotic oscillations [66]. Aperiodic chemical oscillations are the cause of chemical turbulence [78]. Small initial changes in a cell such as a mutation of a cancer driving gene can lead to enormous downstream signaling effects; this is also an example of the butterfly effect. The accumulation of minor mutational events leads to a consecutive loss of mitotic control [75]. Mutations disturb the system; the accumulation of mutations leads to increasing genomic instability. These events in turn effect a change in cellular stability repeatedly until a critical point is reached, after which the system displays chaotic behavior [79]. This is like the example we gave above, when accumulated small changes cause the explosion of the balloon after exceeding a threshold [76].
Now, let's turn to the FTU. In an FTU, when we look at the extreme levels of the diagram, there is aging and increase of entropy outside the optimum cellular function. On the other side, at the extreme level of proliferation, there is chaos. Chaos of the lower level may be associated with the entropy increase of upper level (Figure 6) [35]. For example, mitochondrial level (organelle-level) chaos may alter the bioenergetic state of the cell; increased ROS (reactive oxygen species) production may impair the activity of some transcription factors, such as hypoxia-induced factor (HIF-1alpha), and ultimately can stimulate cancer proliferation at the cellular level [35]. Cellular-level chaos in cancer leads to the disruption of tissue-level organization; this presents clinically as organ cancer. Cancer, therefore, emerges at the level of the unhealthy (dysfunctional) FTU [35]. We will give some other examples of organelle-level chaos at the end of this section.
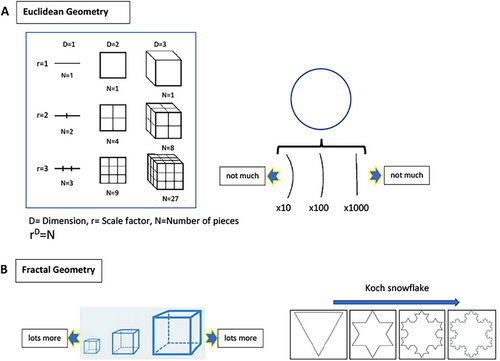
Deterministic chaos is a common behavior in continuous systems with dimensions of three or more [80]. Chaos is basically pure mathematics [36]. In the detection of chaotic behavior for a nonlinear dynamic system, Lyapunov exponents and fractal dimension are the most robust classical mathematical measures [66]. The Lyapunov exponent is a quantity that characterizes the rate of separation of extremely close trajectories in mathematics. Positive Lyapunov exponents are robust signatures of chaos [66]. The word fractal was introduced and defined for the first time by Mandelbrot and means fragmented [66, 75, 81]. Fractal geometry is different from the linear, Euclidean geometric concept (Figure 7). This is a geometry that is formed from chaos [82]. Fractals are universal patterns exhibiting repetitive self-similarity across many different scales. They have symmetry with respect to scale in infinite length, rough contours, and a fractal dimension [75]. Fractals may be infinitely small or infinitely large. Topological dimensions in Euclidean geometry are 0 for a point, 1 dimension (D) for a line, 2-D for a plane (circle, square), and 3-D for a space (spheres) [75]. Fractals have noninteger dimensions; a fractal line has a dimension between one and two, and a fractal surface has a dimension between two and three. Nature normally contains many fractal structures: trees, ferns, cauliflower, snowflakes, beehives, clouds, mountain ranges, the coastlines of geographic landscapes, earthquake faults, or anatomical structures, such as bronchi, the branching of blood vessels, and dendrites [36, 66, 75]. As Baranger explained, nature is full of fractals, and we live among fractals feeling much more comfortable among them than among the figures from elementary geometry [36]. A system exhibiting fractal architecture is robust to environmental changes [66]. Fractals serve as a robust measure of both complexity and chaos. The complexity in the chaos is not algorithmic, and a very short program is required here [66]. Chaos can be a property of very simple systems [36]. Fractal patterns can spontaneously emerge from simple recursive rules [66]. Every chaotic dynamical system is a fractal-producing machine [36]. Complexity and chaos have in common the property of nonlinearity; nonlinearity is a necessary condition for chaos [36]. Every nonlinear system may be chaotic some of the time; complexity implies the presence of chaos, but the reverse is not true; not all complex systems are chaotic [36]. The field of chaos is a very small subfield of the field of complexity [36]. Fractal geometry explains the paradox of how strange attractors compress infinite curves into a finite space (small area or volume) [66]. This is a natural adaptive strategy for resource optimization.
The complex adaptive systems, such as living beings, are capable of changing themselves to adapt to a changing environment [36]. Critical dynamics in complex systems may permit the coexistence of robustness and adaptability in cellular systems [66]. Therefore, both the stability of cell fates and the epigenetic switching among multiple network states in response to environmental fluctuations are possible. A critical point lies at the boundary between these two phases that have different behaviors and rules. Criticality may be an indicator of the potential for a complex system to transition to chaotic behavior [66]. Bifurcation is a critical transition time in the state-space [78]. The critical points indicate regions where the attractors governing its phase-space dynamics are located [66, 83].
There is a growing body of evidence to suggest that cancer is a chaotic disease [31, 35, 66, 74–76, 78–80, 84, 85]. Fractal pattern has been demonstrated in solid tumors (Merkel cell carcinoma, cervix uteri carcinoma, breast cancer, polyps, and colorectal cancer) and hematologic malignancies (AML, CML, and lymphomas) [31, 76, 86–91]. We know that tumor vasculature demonstrates fractal behavior, and cancer angiogenesis is chaotic [84, 85, 92].
Dokukin et al. found that when the tumor perimeters and the distribution of adhesive properties were analyzed by atomic force microscopy, fractal pattern occurred only at a limited period in carcinogenesis; fractal geometry on the cell surface of human cervical epithelial cells was reached only at a particular stage when premalignant (immortal) cells were transformed into cancerous cells; further cancer progression demonstrates deviation from fractal [88]. They previously found that cancer cells demonstrate simple fractal behavior, whereas normal cells can be multifractal [87]. Both cancer and normal cells have good fractal behavior, but fractal dimensionality (FD) is different; cancerous cells have higher FD than normal cells [87]. As we mentioned above, many healthy tissues have fractal patterns, such as the bronchial tree, blood vessels, neural networks, and pancreatic islets [36, 66, 75, 93–95]. Many physiological processes and tumor growth are governed by nonlinear power laws, but their parameters of order and fractal appearances are different [75, 96].
An interesting topic of discussion is about the difference between physiologic fractal pattern and cancer-specific fractal geometry during chaodynamic carcinogenesis. On the basis of natural fractal structures, Dalgleish thinks that cancer is the loss of a normal chaotic system resulting in further chaos, and that a physiologic chaotic system is a necessity for life [74]. Parallel to this idea, Goldberger et al. showed that normal human heartbeat fluctuates in a complex manner; they have a fractal feature of chaotic dynamics [97-99]. They analyzed the time-series plots, Fourier spectra, and phase-space representations for the normal heartbeat, and they observed that the dynamics of the normal heartbeat may be chaotic [97]. This nonlinearity appears advantageous for rapid adaptation and variability. Fractal-like structures play a vital role in the healthy mechanical and electrical dynamics of the heart. Fractal structures are robust and resistant to injury. Inversely, disease and aging may decrease the degree of chaos. Decreased variability and accentuated periodicity are associated with disease. The absolute regularity of heartbeats is just before death [74]. The term “chaos” does not actually mean total randomness and disorder, but it suggests the presence of hidden order within apparent disorder [100]. For this reason, the expression “deterministic chaos” is more appropriate. Chaotic regimes are generally unwanted phenomena and should be avoided or at least controlled [101]. As we mentioned previously, multicellular organisms have periodic oscillations in many physiological events; Claude Bernard in 1849 and W. Bradford Cannon in 1926 defined homeostasis as a condition that may vary but remains relatively constant in biology [102, 103]. It seems that homeostatic ranges are variables and may show fractal features in healthy situations. Homeodynamism or homeodynamic stability may be a more appropriate term to describe this dynamic nature and plasticity of physiological events in complex adaptive systems [103].
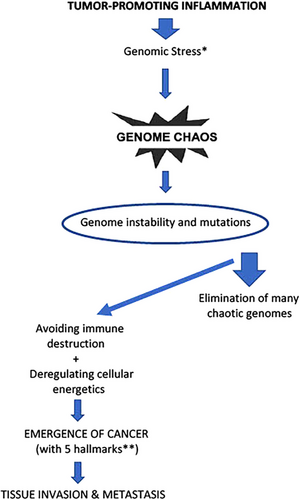
Current, generally accepted theories on cancer development focus on driver mutations affecting oncogenes or tumor suppressor genes or epigenetic changes [2–4, 104]. Today, genome sequencing and expression array analysis make possible the analysis of the expression of thousands of genes in thousands of tumors [105]. As Weinberg stated, despite an explosive increase in the list of oncogene and tumor suppressor genes in the 1980s and 1990s and accumulated big data, the construction of truly useful algorithms on the operation of complex biological machines such as human cells still seems to lie in the distant future, and we need the conceptual paradigms [105]. On the other hand, mutations are not always accidents but are useful sometimes; genetic variability is an indispensable property of life [104]. Endogenous molecular–cellular network is shaped by the hundreds of million-year evolution of multicellular organisms [106]. Evolution would not be possible without the imperfection and vulnerability of the genetic code [104]. Today, the antibody diversity induced by the mutation of the immunoglobulin light chains necessary for survival within the immune system and polyploidization during wound healing are the best examples of genomic adaptation power [104, 107]. Chromosomal or genome-level chaos is observed both in experimental systems and clinical samples in cancers [108-110]. High-level cellular stress triggers chromosome fragmentation (C-Frag); cells then undergo either cell death or rapidly assemble chaotic chromosomes and genome reorganization, and more stable karyotypes are stochastically selected and survive [109]. Many chaotic genomes are eliminated during cancer evolution [109]. If cells survive, stress-induced genome chaos creates new system information, and this is also essential for the emergence of macroevolution [110]. Nature is extremely conservative regarding chromosomes for each species, reproduction enforces conservation of a species-specific karyotype, embryonic development depends on absolute chromosomal conformity, and cells containing altered chromosomes are almost never viable [108]. The karyotypes of cells in many solid tumors are aneuploid. Carcinogens induce aneuploidy, and aneuploid cells reshuffle their chromosomes much faster than mutations can alter their genes [108]. We can conclude that cancer is an evolutionary process; it is a disease of system emergence with a new genome induced by genome chaos [110]. Complexity progressively collapses in cancer [104]. Figure 8 shows an overly simple comparison of evolution and cancer evolution under environmental stress.
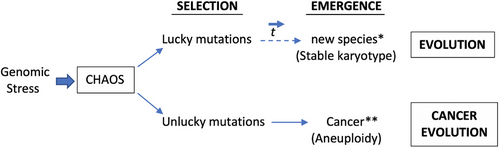
Genome chaos is a sequential process involving multiple cycles [109]. Exposure of cells to high-level stress, such as external (carcinogens or cytotoxic drugs) and/or internal (such as gene mutations and telomere shortening), can induce genome chaos [109]. Chaotic genomes can be defined by extreme structural and numerical alterations of chromosomes. This stress-induced chromosomal instability (CIN) or aneuploidy produces chaotic genomes. Multiple different types of chaos were observed at various time points; genome chaos is not static, but it is a continuous highly dynamic evolutionary process [109]. Newly formed most chaotic genomes are unstable and do not survive. Successful survivors are selected with restructured genome systems and new system inheritance. Finally, selected karyotypes are more stable and less chaotic. We can understand carcinogenesis as a macro-cellular evolutionary process, and evolutionary mechanism has the capability to unify the hallmarks of cancer [111]. It seems that it is not possible to understand carcinogenesis without understanding evolution. On the other hand, understanding the dynamics of cancer may reveal some clues to evolution (Figure 8) [104, 112, 113]. High-dimensional, nonlinear dynamical systems exhibit multiple stable steady states (attractors) far from thermodynamic equilibrium [114]. Each attractor state represents a cell type, and transitions between attractor states correspond to temporal cellular phenotype changes, such as healthy state, immortalization, cancer, metastatic, or drug-resistant phenotype. State transition of genomes or transcriptomes with critical points can be shown as schematic diagrams (functional landscapes), which were first proposed by Waddington as a metaphor [106, 114–116]. Figure 9 summarizes genome chaos, transitional states, and temporal cancer evolution according to the key references [106, 108–111, 114–116].
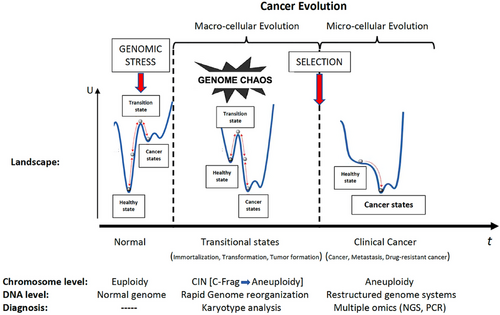
During carcinogenesis, we can differentiate several phases chronologically: immortalization, tumor formation, and cancer. These are compatible with standard steps: initiation, promotion, and progression. Aneuploidy is a cornerstone of progression. A recent study indicated that defective mismatch repair (dMMR)/microsatellite instability high (MSI-H) colorectal cancer presented with significantly lower levels of CIN compared with proficient mismatch repair (pMMR)/microsatellite stable (MSS) tumors in a total of 75 cases (63 of them were stages II and III) [117]. We know that early-stage dMMR/MSI-H patients have good prognosis; these findings may support the importance of CIN for aggressive behavior. Biological organizations and their underlying genetic networks may be ordered, critical, or chaotic in time. Eukaryotic cells in healthy state are dynamically ordered or critical but not chaotic [118]. They also have the potential of plasticity. Criticality may be an indicator of the potential of a complex system to transition to chaotic behavior or a phenotypic switch [66, 119]. Critical points lie at the boundary among these phases that have different behaviors and rules. Adding genome chaos period and phase transitions may complete the standard chronological stepwise model of carcinogenesis (Figure 9). It is time to place the different hallmarks before and after genome chaos; it is obvious that invasion and metastasis will occur after chaos, and tumor-promoting inflammation is before chaos (Figure 10). Thus, we can say that CIN or aneuploidy (genome instability) is in true place (between promotion and progression) in the center during carcinogenesis (Figure 9).
After the chaos theory, some new hypotheses about the origin of life have been developed. In 1990, Kauffman, on the basis of computer simulations and using random Boolean networks as models of disordered dynamical systems, proposed his famous hypothesis: “Life exists on the edge of chaos and order” [120, 121]. Boolean networks are composed of binary “on/off” variables. Networks contain many variables (e.g., genes). The evolvability of complex nonlinear dynamical systems like living organisms that interact with external worlds is possible from the percolation of emergent frozen components among the co-adapting entities in the system [120]. Recently, Gecow et al. proposed the term “half-chaos” to explain the evolution of life that is not in fully random networks; they say that life is the maintenance of half-chaos while a system is exposed to random changes [121]. In the situation of half-chaos, very small disturbances are ordered, very large damage is chaotic, and the loss of half-chaos is a model of death and elimination.
As we mentioned before, another example of organelle-level chaos is mitochondrial chaos [122]. Between networks of insulin receptors and mitochondria, a chaos model for Type 2 diabetes is possible. On the other hand, high-level chronic endoplasmic reticulum stress due to the accumulation of misfolded proteins and defects of homeostatic unfolded protein response may also be associated with the emergence of cancer [22, 47, 48, 123].
7 Is Chaos Control Possible?
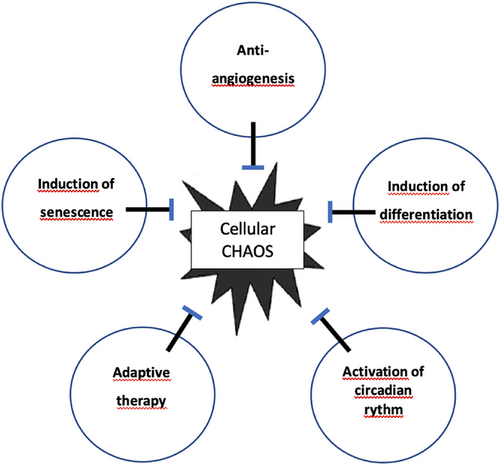
The simple answer is yes. The extreme sensitivity of chaotic systems to initial conditions also makes them highly susceptible to control [124]. The best example of biological chaos control is cardiac ventricular defibrillation. Cardiac chaos control is possible by administering electrical stimuli to the heart; the arrhythmia is converted to periodic beating [124, 125]. Chaos control in epileptic brain was also demonstrated experimentally; electrical stimulation can increase the periodicity in the neuronal population [126]. We can give some successful examples of biologic chaos control. These are anti-angiogenesis, differentiation induction, senescence induction, activating circadian rhythm, and adaptive therapy (Figure 11).
7.1 Anti-Angiogenesis
Inducing angiogenesis is one of the hallmarks of cancer [2, 3]. During tumor progression, an angiogenic switch is activated, and the main angiogenesis inducer is vascular endothelial growth factor-A (VEGF-A), and VEGF signals via three receptor tyrosine kinases (VEGFR 1–3) [3]. A wide variety of medicines (monoclonal antibodies and tyrosine kinase inhibitors) were designed to target this ligand and its receptors. As we mentioned above, angiogenesis (neovascularization) in cancer is a chaotic process; new blood vessels are structurally abnormal, tortuous, irregular, and leaky [84, 85, 92, 127, 128]. Anti-angiogenic therapy targeting the VEGF signaling pathway normalizes blood vessels and decreases vascular permeability and interstitial fluid pressure [127]. Anti-VEGF treatment is a tumor-agnostic strategy, and drugs targeting this pathway have increased survival in patients with several different cancer types in combination with other therapies [128].
7.2 Induction of Differentiation
The revolutionary example of the induction of differentiation is the treatment of acute promyelocytic leukemia (APL) by all-trans-retinoic acid (ATRA) [129-131]. ATRA is an important active metabolite of vitamin A, which promotes the differentiation of APL cells into granulocytes in vitro and significantly improves the complete remission rate of APL [131]. In the first study, which was published in 1988, 24 patients received ATRA alone, and 23 of these patients achieved complete remission [130]. Subsequent trials confirmed the effectiveness of ATRA, and the 2023 edition of the National Comprehensive Cancer Network (NCCN) guidelines recommends ATRA combined with ATO (arsenic trioxide) therapy as Category 1 for the first-line treatment of APL [131, 132]. Another example to promote the differentiation is the use of stem cell differentiation stage factors (SCDSFs) that may be able to reprogram cancer cells [133, 134]. These factors obtained from zebrafish embryos and published first clinical trials are promising [134].
7.3 Senescence Induction (Pro-Senescence Therapy)
Cancer and aging can be regarded as two different manifestations of the same underlying process: the accumulation of cellular damage [25]. Senescent cells exhibit a senescence-associated secretory phenotype (SASP), which is characterized by increased production of growth factors, proteases, and proinflammatory cytokines that recruit immune cells and stimulate them to clear the senescent cells [135, 136]. In a recent study, Ruscetti et al. showed that the combination of a MEK inhibitor trametinib and a CDK4/6 inhibitor palbociclib promoted Rb protein–mediated cellular senescence and the activation of SASP in Kras-mutant lung adenocarcinoma cells while simultaneously provoking a NK cell surveillance program leading to tumor cell death [137]. This was related to tumor regressions and prolonged survival in a Kras-mutant lung adenocarcinoma mouse model. On the contrary, there are some opposite observations depending on the stimulation of tumor development and malignant progression related to senescent cells [138]. Therefore, some unresolved questions exist related to the tumor-antagonizing versus tumor-promoting SASP [4]. Senescence-inducing therapies should be considered carefully [138].
7.4 Activation of Circadian Rhythm
As we mentioned above, human organism is a multi-oscillator, and sustained oscillations occur at all levels of biological organization [65, 139]. The activity and functions of living organisms manifest as periodic or rhythmic variations in relation to the environment; these are biological rhythms [140]. These rhythms are genetically determined. The seminal discoveries of Jeffrey C. Hall, Michael Rosbash, and Michael W. Young elucidated circadian biology [141]. In mammals, circadian rhythms are generated by a master biological clock, located in the suprachiasmatic nucleus (SCN) of the hypothalamus [140, 141]. This central clock regulates circadian rhythms across the entire body via humoral factors and the peripheral autonomic nervous system [141]. Melatonin, which is the main secretory product of the pineal gland, transmits the information of environmental light and darkness to all tissues of the body. Its production is periodic in all mammalian species; its high values are during the dark phase [142]. Normal peak concentrations of melatonin in humans are around 60–80 pg/mL at night (02:00–03:00 a.m.) [143, 144]. The rhythm of melatonin production is generated by the activity of the SCN by a closed loop negative feedback of clock–gene expression [142]. When eyes receive light from the sun, the production of melatonin is inhibited, and the hormones produced keep the organism awake. Retinal ganglion cells containing melanopsin pigment are thought to be the photoreceptors, and the photic information is transmitted to the central pacemaker in the SCN [142]. Epidemiological, experimental, and several clinical trials show that alterations in the circadian rhythms are a risk factor for the development of cancer [140]. Tumor cells have altered circadian machinery compared to normal healthy cells [145]. IARC classified night-shift work, which involves circadian disruption, as a probable (Category 2A) carcinogen [142]. Beside the chronobiotic effect, melatonin has anti-proliferative effects on human cancer cells and acts as an oncostatic agent [142]. Melatonin has a wide variety of functions, which are anti-angiogenesis, neuroendocrine differentiation, cell-cycle arrest, pro-apoptosis, antioxidant, immunomodulatory, proteasome inhibition, aromatase inhibition, and telomerase inhibition [142, 145, 146]. Melatonin downregulates the long-interspersed element (L1), which is a transposable element in human genome, and in this way has a protective effect for genomic stability [146]. It has three membrane receptors (MT1, MT2 in human and other mammals, and MT3 in amphibia and birds), and its mechanisms of action are either receptor-mediated or receptor-independent [144, 146, 147]. Clinical trials revealed that melatonin is an effective adjuvant drug to all conventional therapies, but it is still the subject of research and not in use in routine clinical practice [148]. On the other hand, it has been shown that treatments inducing circadian rhythmicity, such as dexamethasone, forskolin, and heat shock, may activate the circadian clock in cancer cells, which regulates the circadian expression of cell cycle checkpoint genes (especially during G1-S transition), which results in slower tumor growth in experimental studies [149, 150].
7.5 Adaptive Therapy
Cancers are temporal and spatial highly dynamic systems, but cancer treatment today is based on fixed, linear protocols [151]. The main aim of conventional systemic therapy is to kill the maximum possible number of tumor cells. Initially, the fitter chemosensitive cells proliferate against the less fit chemoresistant cells. Theoretically, if the first-line treatment kills a maximum number of sensitive cells, the inhibitory effect of this cellular population on resistant cells is removed, and this situation promotes more rapid growth of the resistant population. Gatenby et al. tried an alternative approach in which treatment is continuously modulated to achieve a fixed stable volume of mostly sensitive population [151]. They called this approach adaptive therapy. The goal here was to maintain a stable tumor burden by permitting mostly sensitive cells to survive so that they suppress the proliferation of the less fit but chemoresistant subpopulations. They presented the first mathematical analysis and demonstrated the feasibility of adaptive therapy by in vivo experiments. This is a different concept than metronomic therapy. Adaptive therapy could achieve a substantially longer survival than conventional and metronomic therapies as well. The general principle of adaptive therapy is that cancer treatment should also be as dynamic as the tumor populations treated. Adaptation of tumor cells should be considered through the continuous adjustment of drugs, doses, and timing. The aim of adaptive therapy, which is to integrate evolutionary principles into clinical cancer treatment protocols, is more natural than brutal high-dose therapies [152]. Some clinical trials with adaptive therapy designs have started and are ongoing [153].
8 A New Treatment Planning in Cancer
If we look at cancer as a chaotic disease, even for a limited period, we propose that chaos control should be done level by level. During chaos control, safety as well as the protection of normal healthy tissues are important issues.
Organ-level treatment is surgery. It gives a cure for many early-stage and some oligometastatic solid tumors. Surgeons are organ-level biologic chaos controllers.
Tissue-level chaos control: The best example is anti-angiogenesis. Another example is the use of somatostatin receptor inhibitors (octreotide, lanreotide, and pasireotide) for neuroendocrine tissue (NET) tumors [154]. Somatostatin receptors are specific for NETs. Similarly, hormonal treatments in breast and prostate cancers are also tissue-specific chaos control instruments. Monoclonal antibodies such as rituximab against CD20 on B lymphocytes for diffuse large B cell lymphomas (DLBCLs) are another example for tissue-level chaos control [155]. We should learn and need other more specific tissue markers and targeted drugs especially for epithelial and connective tissues.
Cellular- and intercellular-level controls: Cytotoxic chemotherapy is a tool of cellular-level chaos control. Adjuvant chemotherapy can be thought of as a cellular-level treatment of chaos after the surgical removal of organ-level chaos. Immunotherapy is also cellular microenvironment treatment. It is based on the intercellular communication between tumor cells and immune effector cells. In recent years, adjuvant immunotherapy, like adjuvant chemotherapy, has been shown to have significant survival benefits in some cancers and has taken its place as standard treatment [156-158]. Host immune system successfully limit the proliferation of small cancers, which frequently emerge naturally; autopsy studies in people and animals who have died from non-cancerous causes support this hypothesis [152].
Organelle-level therapies have not yet been specifically explored, but mitochondrial stress and dysfunction and chronic endoplasmic reticulum stress are associated with cancer [123, 159, 160]. There is a potential of targeting mitochondrial stress response as an anti-cancer strategy [159]. On the other hand, the mitochondrial inhibitor metformin has been the subject of multiple clinical trials in cancer treatment; on the basis of first completed trials, it has weak or little anti-cancer effect in standard diabetes dosing [161]. Combining metformin with lactate transport inhibitors (AZD3965 and VB124) enhances the anti-cancer activity of metformin [161].
All targeted treatments are actually molecular-level treatments. Various “omics” science, which is studying genomes, transcriptomes, proteomes, epigenomes, kinomes, methylomes, glycomes, matrisomes, and metabolomes, has generated large data sets, and this reductionist approach has produced a huge amount of information and important new drugs [105, 162, 163]. Expression array analyses can now be permitted to analyze the expression of thousands of genes in thousands of individual cancer cell genomes [105]. Today, we have entered a period of routine and highly prized personalized therapy for cancer [105].
Atomic-level chaos control: All living organisms are made up of atoms. All chemical processes that are the essence of life are at their core quantum physical because they manipulate properties at the nanometer scale level, including ionization and the formation of chemical bonds [164]. Opposite to inanimate systems, there are unique elements in living cells: the existence of meaningful quantum effects in their warm, wet, and noisy environment [164]. We previously mentioned oscillations, and coherence can be the basis of biological oscillators [164, 165]. Quantum biologists support the existence of quantum phenomena (coherence, superposition, entanglement, and tunneling) in living cells [164, 166–169]. As mentioned above in Section 7.2, Biava et al. used SCDSFs for the phenotypic reprograming of cancer cells [133, 134]. This model is based on quantum field theory (QFT); SCDSFs target symmetry breaking that occurs during cancer development [133, 134, 164]. Symmetry-breaking processes may control cell differentiation by governing the phase transitions [164]. Cells are dissipative systems; they survive by exchanging energy and matter with their environment [133]. The coherent effects have been shown to exist in biological water; hydration layers may play an active role in biochemical processes, transmitting information beyond the boundaries of macromolecules [164, 170]. The quantum variables are derived from the electric dipole oscillations of the biomolecules and water [133]. The high water content in cells may have a role in this effect of SCDSFs [147]. SCDSFs enhance the genes Oct-4, Sox-2, c-Myc, TERT, and Bmi-1 [134]. Oct-4, Sox-2, and c-Myc are actually three of four transcription factors (the fourth one is Klf4) identified by Shinya Yamanaka, who is a 2012 Nobel Prize Winner in Physiology or Medicine, for reprograming somatic differentiated cells to become pluripotent [171]. Bmi-1 is a telomerase-independent repressor of cell aging [134].
Today, radiotherapy is a therapy using ionizing radiation (gamma rays and X-rays) and radyonucleid treatments, which are based on the targeted delivery of radioactive atoms, mainly β-emitting particles or highly potent α-emitting particles; these are all atomic-level treatments in oncology [172].
Chaos control at each level should be safe for neighboring normal structures where there is no chaos. This view is also precision medicine.
9 Discussion
Cancer is not a modern disease. It is a disease as old as the history of life. Very recently, two cases of cancer have been published in JAMA Oncology 2019 and Lancet Oncology 2020, respectively: an osteosarcoma in a 240-million-year-old stem-turtle that is thought to be the earliest cancer case ever recorded, and a first case of osteosarcoma in a dinosaur approximately 77.0–75.5 million years ago [173, 174]. In this review, we tried to present an overview on cancer evolution and a thermodynamic approach to understand life and cancer cooperatively. It seems that it is not possible to understand carcinogenesis without understanding evolution. Current somatic gene mutation theory (SMT) is the dominant approach on cancer development; this gene-centric reductionist molecular biology, which is at the core of the current approach to cancer, has achieved great successes in the last four decades, but as stated at the beginning, the war on cancer is not yet won; the proportion of lives saved has increased from just half to two-thirds [6, 7, 104, 105, 133, 163]. On the other hand, its incidence did not show a significant decrease [5, 163]. Today, we have learned that cancer is not a single disease but many different diseases, that a single-somatic mutation cannot explain this complex pathology, and that at least five or more distinct mutant genes are required [6, 105, 175]. Moreover, cancer patients without mutations have also been reported [115, 176, 177]. In addition, non-genotoxic carcinogens have also been described [177-179]. They can induce inflammation, immune suppression, oxidative stress, and epigenetic silencing, leading to aberrant cellular signaling and genomic instability [179]. In one study, researchers found that the adult stem cells of the small intestine carry the same number of mutations as those of the colon [180]. Considering that colon cancer is more frequent than small bowel cancer, this finding supports that carcinogenesis cannot be a process driven only by mutation [133]. Carcinogens, whether or not they cause gene mutations, may induce aneuploidy, and they function as aneuploidogens rather than as mutagens [108]. High-level cellular stress due to chronic carcinogen exposure induces CIN, which produces temporal genomic chaos at the beginning of carcinogenesis. Many chaotic genomes are eliminated. If cells survive, aneuploid cells reshuffle their chromosomes; cells containing new system information after genome reorganization appear as a clinical picture of cancer with a relatively stable karyotype but with collapsed complexity, disorder, and increased entropy [108, 181]. Chaos theory can be used to discover mathematical biomarkers (such as increased temperature, fractal dimension, and correlation dimension) analogous to biological markers [182]. An interesting observation and associated hypothesis are that some tumors are related to the fractal structure of their tissue of origin; the bronchial trees have a fractal structure; most bronchial cancers originate from the first three orders of the bronchial tree, but not trachea, which does not have a fractal program [183]. Histologically, it may be a new and interesting research project of biology where it is necessary to elucidate the fractal structure programs of tissues and the genetic programs of the geometrical cellular structural differences (squamous, cuboidal, columnar, transitional, etc.) between them, if any. We have learned that the fractal dimension is a parameter of chaotic behavior. Does the golden ratio have a place here? This could be another research topic [75].
The purpose of this review is not to have a philosophical discussion in the biology of cancer, but the limitations of SMT and of the reductionist approach are obvious [119]. According to Cambridge MIT physicist Baranger, whom we have previously quoted several times, sensitivity to initial conditions is the death of reductionism [36]. However, one thing that should not be forgotten is that living organisms consist of systematic organizations that have robustness at various levels [118, 184]. Structural stability against a broad range of perturbations is one of the main features of robust systems [184]. But biological systems are characterized by stochastic dynamical phenomena, and as we mentioned before, critical dynamics in complex systems may permit the coexistence of robustness and adaptability in cellular systems [66, 119]. Reductionism is an ideal way to analyze static states or linear events, but it is inadequate for highly interactive and changeable dynamic systems that are rapidly responsive to environmental perturbations [163]. Systems biology, as a holistic approach beyond reductionism, can help us see the big picture [163, 185]. The contrary of robustness is fragility, and the robustness of a tumor as a system is not equal to the robustness of individual tumor cells; they can be more fragile than non-tumor cells to a particular chemotherapy drug [184]. Unlocking phenotypic plasticity is also accepted as a functionally distinct new hallmark of cancer [4].
Besides SMT, which has been the most popular theory of carcinogenesis for nearly 50 years, there are many other alternative theories [35, 106, 108, 110, 186, 187]. According to the tissue organization field theory (TOFT), which is one of the alternative theories, cancer is a disease of tissue organization; carcinogens disrupt cell-to-cell communications, and genetic mutations are not the cause but the result of genomic integrity due to this disrupted tissue organization [186].
One of the fascinating aspects of life is the existence of highly organized molecular machinery functioning for complex processes such as DNA replication, protein synthesis, cell division, and metabolism in living organisms [188]. Finally, the emergence of a new discipline called quantum biology that supports quantum effects has vital importance in living organisms [189]. One of the interesting discoveries is a new quantum critical material that can exist only in highly evolved systems (living organisms); this bio-conductor material is neither a metal nor an insulator [188]. This is a different universal mechanism of charge transport in living matter, and this finding suggests that quantum transport plays a distinguished role in evolution and natural selection. In the coming years, we need to be ready for new biophysical topics such as quantum chaos and energy turbulence in cancer dynamics and quantum criticality in the origin of life [166, 169, 188].
As a result, this review tries to replace some parts that have not yet been placed in the puzzle of carcinogenesis from a different perspective.
- Entropy is unavoidable because this is a physical law!
- Life is possible only in habitable zones in the universe.
- Living organisms are thermodynamically open systems. They are in the nonequilibrium phase. They exchange matter, energy, and entropy.
- Thermodynamic equilibrium is death.
- Importing and storing of information is necessary for a living organism.
- Living organisms are highly ordered, complex, and modular structures.
- Life is a category of emergence like art composed after the integration of the correct modules.
- Cancer is a chaotic disease, at least for a limited period. Carcinogens induce aneuploidy; high-level cellular stress triggers aneuploidy, which leads to genome chaos. Genome chaos reshuffles chromosomes and leads to a new genomic system. These findings support that cancer is an evolutionary disease.
- Biologic chaos control is possible. There are successful examples (anti-angiogenesis, differentiation induction by ATRA, senescence induction, activating circadian rhythm, adaptive therapy), but we are only at the beginning. More efforts are needed to conquer cancer. Chaos control in cancer should be level by level from up to bottom or vice versa; this makes it possible to look at new treatment planning in cancer from a different (e.g., biophysical, modular) perspective.
Acknowledgments
The author expresses his gratitude to Elizabeth A.W. Sigston for her courtesy of Figure 4 and to Ping Ao for his courtesy of Figure 9.
Ethics Statement
The data are not publicly available due to privacy or ethical restrictions.
Conflicts of Interest
The author declares no conflicts of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author.



 , it takes millions of years; *, with gametogenesis and successful reproduction; **, with unsuccessful “soma-to-germline transition” and pseudomeiotic functions [
, it takes millions of years; *, with gametogenesis and successful reproduction; **, with unsuccessful “soma-to-germline transition” and pseudomeiotic functions [
