Bayes' Theorem and Updating of Belief
Abstract
The conditional probability of an event A given an event B is defined as Pr(A ∩ B)/Pr(B). If you start with hypotheses Hi for which your initial assessments of probability (your prior probabilities) are Pr(Hi) and you then observe data, the probability of which is dependent on which of the hypotheses is true (supposing them to be exclusive and exhaustive, so that one and only one of them is true), then Bayes' theorem allows you to update your assessments of probability to posterior probabilities
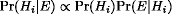
Sometimes we have an unknown parameter that can take any value in a continuous range and the observation we are thinking of can similarly take values from a continuous range. In this case, we get Bayes' theorem for random variables in the form
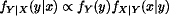
These formulae can be used sequentially, taking the posterior form after one or more observations as the prior for the next.



