On the issue of linearity in chromatic induction by a uniform background

In 1974, Resnikoff proposed a very elegant model for the space of perceived colours 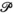based on differential geometry techniques. By adding to Schrödinger's axioms a further hypothesis of homogeneity for 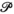, he managed to prove that 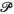can only take two possible forms, one of which is the classical flat trichromatic space, and the other a negatively curved space. The latter has been ignored until recently, when it was used as the starting point for a promising new programme concerning the refoundation of colorimetry. A key step in Resnikoff's construction is the identification of a group of transformations that act transitively on 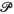as so-called background transformations, that is, changes of the uniform context in which a colour stimulus is embedded. While their transitive nature poses no problem, to the best of the author's knowledge, the hypothesis that these transformations act linearly on the perceived colour associated with the stimulus has never been verified. In this paper, we highlight the importance of the linearity issue in chromatic induction and leave it as an open problem to be discussed by experts in colour, psycho-physics and vision science.