Mixture regression models for closed population capture–recapture data

In capture–recapture studies, the use of individual covariates has been recommended to get stable population estimates. However, some residual heterogeneity might still exist and ignoring such heterogeneity could lead to underestimating the population size (N). In this work, we explore two new models with capture probabilities depending on both covariates and unobserved random effects, to estimate the size of a population. Inference techniques including Horvitz–Thompson estimate and confidence intervals for the population size, are derived. The selection of a particular model is carried out using the Akaike information criterion (AIC). First, we extend the random effect model of Darroch et al. (1993, Journal of American Statistical Association 88, 1137–1148) to handle unit level covariates and discuss its limitations. The second approach is a generalization of the traditional zero-truncated binomial model that includes a random effect to account for an unobserved heterogeneity. This approach provides useful tools for inference about N, since key quantities such as moments, likelihood functions and estimates of N and their standard errors have closed form expressions. Several models for the unobserved heterogeneity are available and the marginal capture probability is expressed using the Logit and the complementary Log–Log link functions. The sensitivity of the inference to the specification of a model is also investigated through simulations. A numerical example is presented. We compare the performance of the proposed estimator with that obtained under model 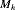of Huggins (1989 Biometrika 76, 130–140).