Adaptive finite-time super-twisting sliding mode control for robotic manipulators with control backlash
Zeyu Li
Key Laboratory of Measurement and Control of CSE, Ministry of Education, School of Automation, Southeast University, Nanjing, China
Search for more papers by this authorCorresponding Author
Junyong Zhai
Key Laboratory of Measurement and Control of CSE, Ministry of Education, School of Automation, Southeast University, Nanjing, China
Correspondence Junyong Zhai, School of Automation, Southeast University, Nanjing 210096, Jiangsu, China.
Email: [email protected]
Search for more papers by this authorHamid Reza Karimi
Department of Mechanical Engineering, Politecnico di Milano, Milan, Italy
Search for more papers by this authorZeyu Li
Key Laboratory of Measurement and Control of CSE, Ministry of Education, School of Automation, Southeast University, Nanjing, China
Search for more papers by this authorCorresponding Author
Junyong Zhai
Key Laboratory of Measurement and Control of CSE, Ministry of Education, School of Automation, Southeast University, Nanjing, China
Correspondence Junyong Zhai, School of Automation, Southeast University, Nanjing 210096, Jiangsu, China.
Email: [email protected]
Search for more papers by this authorHamid Reza Karimi
Department of Mechanical Engineering, Politecnico di Milano, Milan, Italy
Search for more papers by this authorFunding information: National Natural Science Foundation of China, 61873061; Natural Science Foundation of Jiangsu Province, BK20210064
Abstract
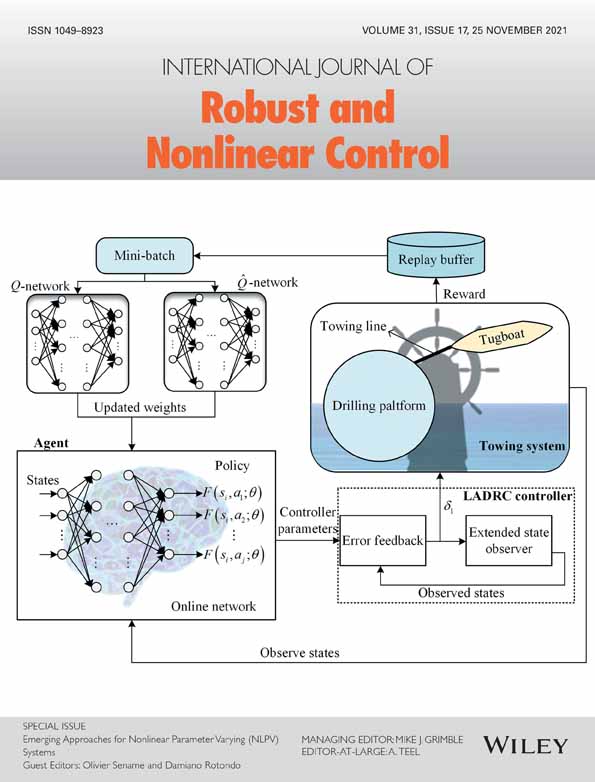
This article aims at the problem of trajectory tracking for industrial robotic manipulators with control backlash. An arctangent terminal sliding mode surface is developed to deal with the lumped disturbance and enhance the robustness of the system. A novel adaptive super-twisting sliding mode control method is developed to achieve fast convergence and continuous control. The chattering in control law is surmounted by using super-twisting method. The lumped disturbance with unknown upper bound is compensated with the help of the adaptive technique. Based on the Lyapunov stability theory, the sliding mode surface will be arrived in a finite time and the trajectory tracking error will converge to zero in a finite time. The feasibility of the proposed control scheme is validated through an example of a two-link robotic manipulator.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interests regarding the publication of this article.
Open Research
DATA AVAILABILITY STATEMENT
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
REFERENCES
- 1Rocco P. Stability of PID control for industrial robot arms. IEEE Trans Robot Automat. 1996; 12(2): 606-614.
10.1109/70.508444 Google Scholar
- 2Prez M, Espinoza A, Romero J, Prez G. On the adaptive control of robot manipulators with velocity observers. Int J Robust Nonlinear Control. 2020; 30(11): 4371-4396.
- 3Wu Z, Karimi HR, Shi P. Practical trajectory tracking of random Lagrange systems. Automatica. 2019; 105: 314-322.
- 4Zheng K, Zhang Q, Hu Y, Wu B. Design of fuzzy system-fuzzy neural network-backstepping control for complex robot system. Inf Sci. 2021; 546: 1230-1255.
- 5Kim E. Output feedback tracking control of robot manipulators with model uncertainty via adaptive fuzzy logic. IEEE Trans Fuzzy Syst. 2004; 12(3): 368-378.
- 6Slotine J, Sastry S. Tracking control of non-linear systems using sliding surfaces, with application to robot manipulators. Int J Control. 1983; 38(2): 465-492.
- 7Zhao L, Cheng H, Wang T. Sliding mode control for a two-joint coupling nonlinear system based on extended state observer. ISA Trans. 2018; 73: 130-140.
- 8
Utkin V, Guldner J, Shi J. Sliding Mode Control in Electro-Mechanical Systems. 2nd ed. CRC Press; 2017.
10.1201/9781420065619 Google Scholar
- 9Obeid H, Laghrouche S, Fridman L. Dual layer barrier functions based adaptive higher order sliding mode control. Int J Robust Nonlinear Control. 2021; 31(9): 3795-3808.
- 10 Zhai J, Li Z. Fast-exponential sliding mode control of robotic manipulator with super-twisting method. IEEE Trans Circ Syst II. 2021. https://doi.org/10.1109/TCSII.2021.3081147
- 11Yi S, Zhai J. Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators. ISA Trans. 2019; 90: 41-51.
- 12Rubio JJ, Ochoa G, Mujica-Vargas D, et al. Structure regulator for the perturbations attenuation in a quadrotor. IEEE Access. 2019; 7(1): 138244-138252.
- 13Escobedo-alva JO, Garcia-estrada EC, Paramo-carranza LA, Meda-campana JA, Tapia-Herrera R. Theoretical application of a hybrid observer on altitude tracking of quadrotor losing GPS signal. IEEE Access. 2020; 6(1): 76900-76908.
- 14Marino R, Tomei P. Adaptive observers with arbitrary exponential rate of convergence for nonlinear systems. IEEE Trans Automat Contr. 1995; 40(7): 1300-1304.
- 15Parra-Vega V, Castillo-Tapia A, Arteaga-Prez MA. Regressorfree second order sliding mode control for exponential tracking of constrained robot manipulators. Proceedings of the 3rd International Workshop on Robot Motion and Control, Bukowy Dworek, Poland; 2002:159-164.
- 16Man Z, Paplinski A, Wu H. A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans Automat Contr. 1994; 39(12): 2464-2469.
- 17Tang Y. Terminal sliding mode control for rigid robots. Automatica. 1998; 34(1): 51-56.
- 18Yu S, Yu X, Shirinzadeh B, Man Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica. 2005; 41(11): 1957-1964.
- 19Wang L, Chai T, Zhai L. Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics. IEEE Trans Ind Electron. 2009; 56(9): 3296-3304.
- 20Lu K, Xia Y. Adaptive attitude tracking control for rigid spacecraft with finite-time convergence. Automatica. 2013; 49(12): 3591-3599.
- 21Van M, Ge SS, Ren H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans Cybern. 2017; 47(7): 1681-1693.
- 22Zhai J, Song Z. Adaptive sliding mode trajectory tracking control for wheeled mobile robots. Int J Control. 2019; 92(10): 2255-2262.
- 23Boukattaya M, Mezghani N, Damak T. Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 2018; 77: 1-19.
- 24Ma H, Li Y. A novel dead zone reaching law of discrete-time sliding mode control with disturbance compensation. IEEE Trans Ind Electron. 2020; 67(6): 4815-4825.
- 25Xu G, Zhai J. Adaptive fast non-singular terminal sliding mode control for robotic manipulators with deadzone. Proceedings of the 39th Chinese Control Conference; 2020:364-369; Shenyang, China.
- 26Rubio JJ. Sliding mode control of robotic arms with deadzone. IET Control Theory Appl. 2017; 11(8): 1214-1221.
- 27Zhou X, Wang H, Tian Y, Zheng G. Disturbance observer-based adaptive boundary iterative learning control for a rigid-flexible manipulator with input backlash and endpoint constraint. Int J Adapt Control Signal Process. 2020; 34(9): 1220-1241.
- 28Sun G, Zhao J, Chen Q. Observer-based compensation control of servo systems with backlash. Asian J Control. 2021; 23(1): 499-512.
- 29Aguilar LT, Orlov Y, Cadiou JC, Merzouki R. Nonlinear H
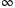 -output regulation of a nonminimum phase servomechanism with backlash. J Dyn Syst Meas Control. 2007; 129(4): 544-549.
-output regulation of a nonminimum phase servomechanism with backlash. J Dyn Syst Meas Control. 2007; 129(4): 544-549.
- 30Martinez DI, Rubio JJ, Vargas TM, et al. Stabilization of robots with a regulator containing the sigmoid mapping. IEEE Access. 2020; 8(1): 89479-89488.
- 31Levant A. Sliding order and sliding accuracy in sliding mode control. Int J Control. 1993; 58(6): 1247-1263.
- 32Chalanga A, Kamal S, Fridman L, Bandyopadhyay B, Moreno J. Implementation of super-twisting control: super-twisting and higher order sliding-mode observer-based approaches. IEEE Trans Ind Electron. 2016; 63(6): 3677-3685.
- 33Zhang L, Liu L, Wang Z, Xia Y. Continuous finite-time control for uncertain robot manipulators with integral sliding mode. IET Control Theory Appl. 2018; 12(11): 1621-1627.
- 34Utkin V, Poznyak A. Adaptive sliding mode control with application to super-twist algorithm: Equivalent control method. Automatica. 2013; 49(1): 39-47.
- 35Plestan F, Shtessel Y, Bregeault V, Poznyak A. New methodologies for adaptive sliding mode control. Int J Control. 2010; 83(9): 1907-1919.
- 36Shtessel Y, Taleb M, Plestan F. A novel adaptive-gain super twisting sliding mode controller: methodology and application. Automatica. 2012; 48(5): 759-769.
- 37Shao K, Zheng J, Huang K, Wang H, Man Z, Fu M. Finite-time control of a linear motor positioner using adaptive recursive terminal sliding mode. IEEE Trans Ind Electron. 2020; 67(8): 6659-6668.
- 38Mondal S, Mahanta C. Adaptive second order terminal sliding mode controller for robotic manipulators. J Frankl Inst. 2014; 351(4): 2356-2377.
- 39Mobayen S, Tchier F, Ragoub L. Design of an adaptive tracker for n-link rigid robotic manipulators based on super-twisting global nonlinear sliding mode control. Int J Syst Sci. 2017; 48(9): 1990-2002.
- 40He S, Lin D, Wang J. Chattering-free adaptive fast convergent terminal sliding mode controllers for position tracking of robotic manipulators. Proc Inst Mech Eng C-J Mech Eng Sci. 2016; 230(4): 514-526.
- 41Hendel R, Khaber F, Essounbouli N. Adaptive high order sliding mode controller/observer based terminal sliding mode for MIMO uncertain nonlinear system. Int J Control. 2019; 94(2): 486-506.
- 42Feng Y, Yu X, Man Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica. 2002; 38(12): 2159-2167.
- 43Yang B, Lin W. Homogeneous observers, iterative design, and global stabilization of high-order nonlinear systems by smooth output feedback. IEEE Trans Automat Contr. 2004; 49(7): 1069-1080.
- 44Bhat S, Bernstein D. Finite-time stability of continuous autonomous systems. SIAM J Control Optim. 2000; 38(3): 751-766.
- 45Zhou X, Wang H, Tian Y, Zheng G. Disturbance observer-based adaptive boundary iterative learning control for a rigid-flexible manipulator with input backlash and endpoint constraint. Int J Adapt Control Signal Proc. 2020; 34(9): 1220-1241.
- 46Zhu W. Comments on “Robust tracking control for rigid robotic manipulators”. IEEE Trans Automat Contr. 2000; 45(8): 1577-1580.
- 47Zhai J, Xu G. A novel non-singular terminal sliding mode trajectory tracking control for robotic manipulators. IEEE Trans Circ Syst II. 2021; 68(1): 391-395.
Citing Literature
Special Issue:Emerging Approaches for Nonlinear Parameter Varying (NLPV) Systems
25 November 2021
Pages 8537-8550