Two-grid methods for 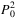–P₁ mixed finite element approximation of general elliptic optimal control problems with low regularity

In this paper, we present a two-grid mixed finite element scheme for distributed optimal control governed by general elliptic equations. 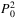–P₁ mixed finite elements are used for the discretization of the state and co-state variables, whereas piecewise constant function is used to approximate the control variable. We first use a new approach to obtain the superclose property between the centroid interpolation and the numerical solution of the optimal control u with order h² under the low regularity. Based on the superclose property, we derive the optimal a priori error estimates. Then, using a postprocessing projection operator, we get a second-order superconvergent result for the control u. Next, we construct a two-grid mixed finite element scheme and analyze a priori error estimates. In the two-grid scheme, the solution of the elliptic optimal control problem on a fine grid is reduced to the solution of the elliptic optimal control problem on a much coarser grid and the solution of a linear algebraic system on the fine grid and the resulting solution still maintains an asymptotically optimal accuracy. Finally, a numerical example is presented to verify the theoretical results.