Dispersive estimates for time and space fractional Schrödinger equations
Xiaoyan Su
Institute of Applied Physics and Computational Mathematics, Beijing, 100094 China
Search for more papers by this authorCorresponding Author
Shiliang Zhao
Department of Mathematics, Sichuan University, Chengdu, 610064 China
Correspondence
Shiliang Zhao, Department of Mathematics, Sichuan University, Chengdu 610064, China.
Email: [email protected]
Communicated by: D. Zeidan
Search for more papers by this authorMiao Li
Department of Mathematics, Sichuan University, Chengdu, 610064 China
Search for more papers by this authorXiaoyan Su
Institute of Applied Physics and Computational Mathematics, Beijing, 100094 China
Search for more papers by this authorCorresponding Author
Shiliang Zhao
Department of Mathematics, Sichuan University, Chengdu, 610064 China
Correspondence
Shiliang Zhao, Department of Mathematics, Sichuan University, Chengdu 610064, China.
Email: [email protected]
Communicated by: D. Zeidan
Search for more papers by this authorMiao Li
Department of Mathematics, Sichuan University, Chengdu, 610064 China
Search for more papers by this authorAbstract
In this paper, we consider the Cauchy problem for the fractional Schrödinger equation
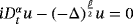with 0 < α < 1, β > 0. We establish the dispersive estimates by a carefully study of the Mittag-Leffler functions and give some applications as well. In particular, we prove that the decay rates are sharp.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
REFERENCES
- 1Mainardi F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models. Singapore: World Scientific; 2010.
10.1142/p614 Google Scholar
- 2Podlubny I. Fractional Differential Equations, Mathematics in Science and Engineering. New York: Academic Press; 1999.
- 3Samko SG, Kilbas AA, Marichev OI. Fractional Integrals and Derivatives: Theory and Applications. Yverdon, Switzerland:Gordon and Breach Science; 1993.
- 4Meerschaert MM, Sikorskii A. Stochastic Models for Fractional Calculus, De Gruyter Studies in Mathematics, vol. 43. Berlin/ Boston: Walter de Gruyter; 2012.
- 5Laskin N. Fractional quantum mechanics and Lévy path integrals. Phys Lett A. 2000; 268: 298-305.
- 6Laskin N. Fractional Schrödinger equation. Phys Rev E. 2002; 66: 56-108.
- 7Laskin N. Time fractional quantum mechanics. Chaos solitons Fractals. 2017; 102: 16-28.
- 8Laskin N. Fractional Quantum Mechanics. Singapore: World Scientific; 2018.
10.1142/10541 Google Scholar
- 9Bourgain J. Global Solutions of Nonlinear Schrödinger Equations, American Mathematical Society Providence, vol. 46. RI: American Mathematical Society Colloquium Publications; 1999.
10.1090/coll/046 Google Scholar
- 10Cazenave T. Semilinear Schrödinger Equations, American Mathematical Society, vol. 10. Providence, RI: Courant Lect Notes Math; 2003.
10.1090/cln/010 Google Scholar
- 11Tao T. Nonlinear Dispersive Equations: Local and Global Analysis, Regional Conference Series in Mathematics. Providence, RI: American Mathematical Society; 2006.
10.1090/cbms/106 Google Scholar
- 12Laskin N. Fractional quantum mechanics. Phys Rev E. 2000; 62: 3135-3145.
- 13Narahari Achar BN, Yale BT, Hanneken JW. Time fractional Schrödinger equation revisited. Adv Math Phys. 2013; 2013: 1-11.
- 14Naber M. Time fractional Schrödinger equation. J Math Phys. 2004; 45: 3339-3352.
- 15Bayin SS. Time fractional Schrödinger equation: Fox's H-functions and the effective potential. J Math Phys. 2013; 54: 31-35.
- 16Wang S, Xu M. Generalised fractional Schrödinger equation with space-time derivatives. J Math Phys. 2007; 48:043502.
- 17Dong J, Xu M. Space-time fractional Schrödinger equation with time dependent potentials. J Math Anal Appl. 2008; 344: 1005-1017.
- 18Duong Dinh V. On the blowup solutions to the focusing L2-supercritical nonlinear fractional Schrödinger equations. arXiv:1802.0289; 2018.
- 19Hong Y, Sire Y. On fractional Schrödinger equations in Sobolev spaces. Commun Pur App Anal. 2015; 14: 2265-2282.
- 20Ionescu A, Pusateri F. Nonlinear fractional Schrödinger equations in one dimension. J Funct Anal. 2014; 266: 139-176.
- 21Sandev T, Petreska I, Lenzi EK. Effective potential from the generalized time-dependent Schrödinger equation. Mathematics. 2016; 4: 59-68.
- 22Cho Y, Ozawa H, Xia S. Remarks on some dispersive estimates. Commun Pur App Anal. 2011; 10: 1121-1128.
- 23Gorenflo R, Kilbas AA, Mainardi F, Rogosin SV. Mittag-Leffler Functions, Related Topics and Applications, Springer Monographs in Mathematics. Verlag Berlin Heidelberg: Springer; 2014.
10.1007/978-3-662-43930-2 Google Scholar
- 24Gerhold S. Asymptotics for a variant of the Mittag-Leffler function. Integral Transforms Spec Funct. 2012; 23: 397-403.
- 25Wang J, Zhou Y, O'Regan D. A note on asymptotic behaviour of Mittag-Leffler functions. Integral Transforms Spec Funct. 2018; 29: 81-94.
- 26Grafakos L. Classical Fourier Analysis, Graduate Texts in Mathematics. New York: Springer; 2008.
10.1007/978-0-387-09432-8 Google Scholar
- 27Bergh J, Löfström J. Interpolation Spaces. Berlin: Springer; 1976.
10.1007/978-3-642-66451-9 Google Scholar
