RESEARCH ARTICLE
Asymptotic behavior to a chemotaxis consumption system with singular sensitivity
Xiangdong Zhao,
Sining Zheng,
Xiangdong Zhao
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China
Search for more papers by this authorCorresponding Author
Sining Zheng
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China
Correspondence
Sining Zheng, School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China.
Email: [email protected]
Search for more papers by this authorXiangdong Zhao,
Sining Zheng,
Xiangdong Zhao
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China
Search for more papers by this authorCorresponding Author
Sining Zheng
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China
Correspondence
Sining Zheng, School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China.
Email: [email protected]
Search for more papers by this authorAbstract
We consider a chemotaxis consumption system with singular sensitivity
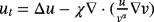, vt=εΔv−uv in a bounded domain
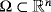with χ,α,ε>0. The global existence of classical solutions is obtained with n=1. Moreover, for any global classical solution (u,v) to the case of n,α≥1, it is shown that v converges to 0 in the L∞-norm as t→∞ with the decay rate established whenever ε∈(ε0,1) with
.
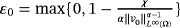REFERENCES
- 1Keller EF, Segel LA. Traveling bands of chemotactic bacteria: a theoretical analysis. J Theoret Biol. 1971; 30: 377-380.
- 2Keller EF, Segel LA. Initiation of slime mold aggregation viewed as an instability. J Theoret Biol. 1970; 26: 399-415.
- 3Nagai T, Senba T. Behavior of radially symmetric solutions of a system related to chemotaxis. Nonlinear Anal. 1997; 30: 3837-3842.
- 4Fujie K, Winkler M, Yokota T. Boundedness of solutions to parabolic-elliptic Keller-Segel systems with signal-dependent sensitivity. Math Methods Appl Sci. 2015; 38: 1212-1224.
- 5Fujie K, Senba T. Global existence and boundedness in a parabolic-elliptic Keller-Segel system with general sensitivity. Discrete Contin Dyn Syst Ser B. 2016; 21: 81-102.
- 6Winkler M. Global solutions in a fully parabolic chemotaxis system with singular sensitivity. Math Methods Appl Sci. 2011; 34: 176-190.
- 7Fujie K. Boundedness in a fully parabolic chemotaxis system with singular sensitivity. J Math Anal Appl. 2015; 424: 675-684.
- 8Fujie K, Senba T. Global existence and boundedness of radial solution to a two dimensional fully parabolic chemotaxis system with general sensitivity. Nonlinearity. 2016; 29: 2417-2450.
- 9Lankeit J, Winkler M. A generalized solution concept for the Keller-Segel system with logarithmic sensitivity: global solvability for large nonradial data. NoDEA Nonlinear Differential Equations Appl. 2017; 24(4):33. Art. 49.
- 10Fujie K, Winkler M, Yokota T. Blow-up prevention by logistic sources in a parabolic-elliptic Keller-Segel system with singular sensitivity. Nonliear Anal. 2014; 109: 56-71.
- 11Lankeit J. A new approach toward boundedness in a two-dimensional parabolic chemotaxis system with singular sensitivity. Math Methods Appl Sci. 2016; 39: 394-404.
- 12Stinner C, Winkler M. Global weak solutions in a chemotaxis system with large singular sensitivity. Nonliear Anal Real World Appl. 2011; 12: 3727-3740.
- 13Zhao XD, Zheng SN. Global boundedness to a chemotaxis system with singular sensitivity and logistic source. Z Angew Math Phys. 2017; 68: 13 Art. 2.
- 14Corrias L, Perthame B, Zaag H. A chemotaxis model motivated by angiogenesis. C R Acad Sci Paris Ser I. 2003; 336: 141-146.
- 15Rascle M. Sur une é,quation integro-différentielle non linéaire issue de la biologie. J Differential Equations. 1979; 32: 420-453.
- 16Corrias L, Perthame B, Zaag H. Global solutions in some chemotaxis and angiogenesis systems in high space dimensions. Milan J Math. 2004; 72: 1-28.
10.1007/s00032-003-0026-x Google Scholar
- 17Rascle M. On a system of non-linear strongly coupled partial differential equations arising in biology. Conf. on Ordinary and Partial Differential Equation, Lectures Notes in Math. 1980; 848: 388-414.
- 18Tao YS, Winkler M. Eventual smoothness and stabilization of large-data solutions in a three-dimensional chemotaxis system with consumption of chemoattractant. J Differential Equations. 2012; 252: 2520-2543.
- 19Tao YS. Boundedness in a chemotaxis model with oxygen consumpution by bacteria. J Math Anal Appl. 2011; 381: 521-529.
- 20Cao XR, Ishida S. Global-in-time bounded weak solutions to a degenerate quasilinear Keller-Segel system with rotation. Nonlinearity. 2014; 27: 1899-1913.
- 21Li T, Suen A, Winkler M, Xue C. Global small-data solutions of a two-dimensional chemotaxis system with rotational flux terms. Math Models Methods Appl Sci. 2015; 25: 721-746.
- 22Winkler M. Large-data global generalized solutions in a chemotaxis system with tensor-valued sesitivities. SIAM J Math Anal. 2015; 47: 3092-3115.
- 23Winkler M. The two-dimensional Keller-Segel system with singular sensitivity and signal absorption: global large-data solutions and their relaxation properties. Math Models Methods Appl Sci. 2016; 26(5): 987-1024.
- 24Winkler M. The two-dimensional Keller-Segel system with singular sensitivity and signal absorption: Eventual smoothness and equilibration of small-mass solutions. preprint; 2016.
- 25Winkler M. Renormalized radial large-data solutions to the higher-dimensional Keller-Segel system with singular sensitivity and signal absorption. J Differential Equations. 2018; 264: 2310-2350.
- 26Lankeit J. Locally bounded global solutions to a chemotaxis consumption model with singular sensitivity and nonlinear diffusion. J Differential Equations. 2017; 262: 4052-4084.
- 27Wang YL. Global large-data generalized solutions in a two-dimensional chemotaxis-Stokes system with singular sensitivity. Bound Value Probl. 2016; 24 Art. 177.
- 28Liu DM. Global classical solution to a chemotaxis consumption model with singular sensitivity. Nonlinear Anal Real World Appl. 2018; 41: 497-508.
- 29Friedman A, Tello I. Stability of solutions of chemotaxis equations in reinforced random walks. J Math Anal Appl. 2002; 272: 138-163.
- 30Winkler M. Aggregation vs. global diffusive behavior in the higher-dimensional Keller-Segel model. J Differential Equations. 2010; 248: 2889-2905.
- 31Cao XR, Lankeit J. Global classical small-data solutions for a three-dimensional chemotaxis Navier-Stokes system involving matrix-valued sensitivities. Calc. Var. Partial Differential Equations. 2016; 55:39. Paper No. 107.
- 32Ladyzenskaja OA, Solonnikov VA, Ural'ceva NN. Linear and Quasi-linear Equations of Parabolic Tpye. Providence RI: AMS; 1968.
10.1090/mmono/023 Google Scholar
