Nonlinear diffusion equations as asymptotic limits of Cahn-Hilliard systems on unbounded domains via Cauchy's criterion

This paper develops an abstract theory for subdifferential operators to give existence and uniqueness of solutions to the initial-boundary problem P for the nonlinear diffusion equation in an unbounded domain 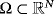( 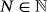), written as

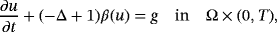
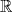which represents the porous media, the fast diffusion equations, etc, where β is a single-valued maximal monotone function on , and T>0. In Kurima and Yokota (J Differential Equations 2017; 263:2024-2050 and Adv Math Sci Appl 2017; 26:221-242) existence and uniqueness of solutions for P were directly proved under a growth condition for β even though the Stefan problem was excluded from examples of P. 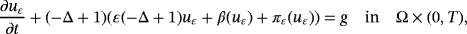This paper completely removes the growth condition for β by confirming Cauchy's criterion for solutions of the following approximate problem _ε with approximate parameter ε>0: 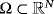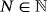which is called the Cahn-Hilliard system, even if ( ) is an unbounded domain. Moreover, it can be seen that the Stefan problem excluded from Kurima and Yokota (J Differential Equations 2017; 263:2024-2050 and Adv Math Sci Appl 2017; 26:221-242) is covered in the framework of this paper.