Research Article
Optimal decay rate of the bipolar Euler–Poisson system with damping in dimension three
Zhigang Wu,
Yuming Qin,
Zhigang Wu
Department of Applied Mathematics, Donghua University, Shanghai, 201620, China
Search for more papers by this authorCorresponding Author
Yuming Qin
Department of Applied Mathematics, Donghua University, Shanghai, 201620, China
Correspondence to: Yuming Qin, Department of Applied Mathematics, Donghua University, Shanghai, 201620, China.
E-mail: [email protected]
Search for more papers by this authorZhigang Wu,
Yuming Qin,
Zhigang Wu
Department of Applied Mathematics, Donghua University, Shanghai, 201620, China
Search for more papers by this authorCorresponding Author
Yuming Qin
Department of Applied Mathematics, Donghua University, Shanghai, 201620, China
Correspondence to: Yuming Qin, Department of Applied Mathematics, Donghua University, Shanghai, 201620, China.
E-mail: [email protected]
Search for more papers by this authorAbstract
By rewriting a bipolar Euler–Poisson equations with damping into a Euler equation with damping coupled with a Euler–Poisson equation with damping and using a new spectral analysis, we obtain the optimal decay results of the solutions in L2 norm. More precisely, the velocities u1 and u2 decay at the L2−rate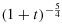 
, which is faster than the normal L2-rate 
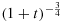for the heat equation and the Navier–Stokes equations. In addition, the decay rates of the disparities of two densities ρ1−ρ2 and the disparity of two velocities u1−u2 could reach to 
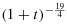and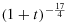 
in L2 norm, respectively. Copyright © 2015 John Wiley & Sons, Ltd.
References
- 1 Li YP, Yang XF. Global existence and asymptotic behavior of the solutions to the three-dimensional bipolar Euler-Poisson systems. Journal of Differential Equations 2012; 252: 768–791.
- 2 Wu ZG, Wang WK. Decay of the solution for the bipolar Euler-Poisson system with damping in dimension three. Communications in Mathematical Sciences 2014; 12(7): 1257–1276.
- 3
Jüngel A. Quasi-Hydrodynamic Semiconductor Equations, Progr. Nonlinear Differential Equations Appl. Birkhäuser, Basel, 2001.
10.1007/978-3-0348-8334-4 Google Scholar
- 4
Markowich PA,
Ringhofev CA,
Schmeiser C. Semiconductor Equations. Springer: Wien, New York, 1990.
10.1007/978-3-7091-6961-2 Google Scholar
- 5 Sitenko A, Malnev V. Plasma Physics Theory. Chapman & Hall: London, 1995.
- 6 Zhou F, Li YP. Existence and some limits of stationary solutions to a one-dimensional bipolar Euler-Poisson system. Journal of Mathematical Analysis and Applications 2009; 351: 480–490.
- 7 Tsuge N. Existence and uniqueness of stationary solutions to a one-dimensional bipolar hydrodynamic models of semiconductors. Nonlinear Analysis 2010; 73: 779–787.
- 8 Li YP. Global existence and asymptotic behavior of smooth solutions to a bipolar Euler-Poisson equations in a bound domain. Zeitschrift fur Angewandte Mathematik und Physik 2013; 64: 1125–1144.
- 9 Natalini R. The bipolar hydrodynamic model for semiconductors and the drift-diffusion equation. Journal of Mathematical Analysis and Applications 1996; 198: 262–281.
- 10 Hsiao L, Zhang KJ. The global weak solution and relaxation limits of the initial boundary value problem to the bipolar hydrodynamic model for semiconductors. Mathematical Models and Methods in Applied Sciences 2000; 10: 1333–1361.
- 11 Huang FM, Li YP. Large time behavior and quasineutral limit of solutions to a bipolar hydrodynamic model with large data and vacuum. Discrete and Continuous Dynamical Systems - Series A 2009; 24: 455–470.
- 12 Hsiao L, Zhang KJ. The relaxation of the hydrodynamic model for semiconductors to the drift-diffusion equations. Journal of Differential Equations 2000; 165: 315–354.
- 13 Gasser I, Marcati P. The combined relaxation and vanishing Debye length limit in the hydrodynamic model for semiconductors. Mathematical Methods in the Applied Sciences 2001; 24: 81–92.
- 14 Zhu C, Hattori H. Stability of steady state solutions for an isentropic hydrodynamic model of semiconductors of two species. Journal of Differential Equations 2000; 166: 1–32.
- 15 Gasser I, Hsiao L, Li HL. Asymptotic behavior of solutions of the bipolar hydrodynamic fluids. Journal of Differential Equations 2003; 192: 326–359.
- 16 Donatelli D, Mei M, Rubino B, Sampalmieri R. Asymptotic behavior of solutions to Euler-Poisson equations for bipolar hydrodynamic model of semiconductors. Journal of Differential Equations 2013; 255: 3150–3184.
- 17 Huang FM, Wang M, Mei Y. Large time behavior of solution to n-dimensional bipolar hydrodynamic model for semiconductors. SIAM Journal on Mathematical Analysis 2011; 43: 1595–1630.
- 18 Lattanzio C. On the 3-D bipolar isentropic Euler-Poisson model for semiconductors and the drift-diffusion limit. Mathematical Models and Methods in Applied Sciences 2000; 10: 351–360.
- 19 Ali G, Chen L. The zero-electron-mass limit in the Euler-Poisson system for both well- and ill-prepared initial data. Nonlinearity 2011; 24: 2745–2761.
- 20 Li YP. Diffusion relaxation limit of a bipolar isentropic hydrodynamic model for semiconductors. Journal of Mathematical Analysis and Applications 2007; 336: 1341–1356.
- 21 Li YP. Relaxation-time limit of the three-dimensional hydrodynamic model with boundary effects. Mathematicsl Methods in the Applied Sciences 2011; 34: 1202–1210.
- 22 Ali G, Jügel A. Global smooth solutions to the multi-dimensional hydrodynamic model for two-carrier plasma. Journal of Differential Equations 2003; 190: 663–685.
- 23 Li YP, Zhang T. Relaxation-time limit of the multidimensional bipolar hydrodynamic model in Besov space. Journal of Differential Equations 2011; 251(11): 3143–3162.
- 24 Ju QC. Global smooth solutions to the multidimensional hydrodynamic model for plasmas with insulating boundary conditions. Journal of Mathematical Analysis and Applications 2007; 336: 888–904.
- 25 Li HL, Matsumura A, Zhang GJ. Optimal decay rate of the compressible Navier-Stokes-Poisson system in R3. Archive for Rational Mechanics and Analysis 2010; 196: 681–713.
- 26
Li HL,
Yang T,
Zou C. Time asymptotic behavior of the bipolar Navier-Stokes-Poisson system. Acta Mathematica Scientia 2009; 29B(6): 1721–1736.
10.1016/S0252-9602(10)60013-6 Google Scholar
- 27 Wang WK, Wu ZG. Pointwise estimates of solution for the Navier-Stokes-Poisson equations in multi-dimensions. Journal of Differential Equations 2010; 248: 1617–1636.
- 28 Wu ZG, Wang WK. Pointwise estimates of solution for non-isentropic Navier-Stokes equations in multi-dimensions. Acta Mathematica Scientia 2012; 32B(5): 1681–1702.
- 29 Wu ZG, Wang WK. Pointwise estimate of solutions for the Euler-Poisson equation with damping in multi-dimensions. Discrete and Continuous Dynamical Systems - Series A 2010; 26(3): 1101–1117.
- 30 Zhang GJ, Li HL, Zhu CJ. Optimal decay rate of the non-isentropic Navier-Stokes-Poisson system in R3. Journal of Differential Equations 2011; 250(2): 866–891.
- 31 Guo Y, Wang YJ. Decay of dissipative equations and negative Sobolev spaces. Communications in Partial Differential Equations 2012; 37: 2165–2208.
- 32 Wang YJ. Decay of the Navier-Stokes-Poisson equations. Journal of Differential Equations 2012; 253: 273–297.
- 33
Tan Z,
Wu GC. Large time behavior of solutions for compressible Euler equations with damping in
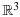. Journal of Differential Equations 2012; 252: 1546–1561.
- 34 Wang WK, Yang T. The pointwise estimates of solutions for Euler Equations with damping in multi-dimensions. Journal of Differential Equations 2001; 173: 410–450.
- 35 Li HL, Zhang KJ, Zhang GJ. Algebra time decay fro the bipolar quantum hydrodynamic model. Mathematical Models and Methods in Applied Sciences 2008; 18: 859–881.
- 36
Tan Z,
Wang Y. Global well-posedness of the compressible bipolar Euler–Maxwell system in
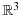, arXiv: 1212.5980v1.
