Existence and uniqueness of solutions of sequential nonlinear fractional difference equations with three-point fractional sum boundary conditions
Corresponding Author
Thanin Sitthiwirattham
Nonlinear Dynamic Analysis Research Center, Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok, Thailand
Correspondence to: Thanin Sitthiwirattham, Nonlinear Dynamic Analysis Research Center, Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok, Thailand
E-mail: [email protected]
Search for more papers by this authorCorresponding Author
Thanin Sitthiwirattham
Nonlinear Dynamic Analysis Research Center, Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok, Thailand
Correspondence to: Thanin Sitthiwirattham, Nonlinear Dynamic Analysis Research Center, Department of Mathematics, Faculty of Applied Science, King Mongkut's University of Technology North Bangkok, Bangkok, Thailand
E-mail: [email protected]
Search for more papers by this authorAbstract
In this paper, we consider a discrete fractional boundary value problem of the form:
, 
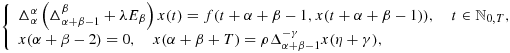
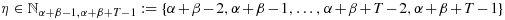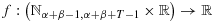is a continuous function, and Eβx(t) = x(t + β − 1). The existence and uniqueness of solutions are proved by using Banach's fixed point theorem. An illustrative example is also presented. Copyright © 2014 John Wiley & Sons, Ltd.
References
- 1 Atici FM, Eloe PW. Two-point boundary value problems for finite fractional difference equations. Journal of Difference Equations and Applications 2011; 17: 445–456.
- 2 Atici FM, Eloe PW. Linear systems of fractional nabla difference equations. Rocky Mountain Journal of Mathematics 2011; 41: 353–370.
- 3 Atici FM, Şengül S. Modeling with fractional difference equations. Journal of Mathematical Analysis and Applications 2010; 369: 1–9.
- 4 Sitthiwirattham T, Tariboon J, Ntouyas SK. Existence results for fractional difference equations with three-point fractional sum boundary conditions. Discrete Dynamics in Nature and Society 2013 10 pages. Article ID 104276.
- 5 Sitthiwirattham T, Tariboon J, Ntouyas SK. Boundary value problems for fractional difference equations with three-point fractional sum boundary conditions. Advances in Difference Equations 2013; 2013: 296.
- 6
Pan Y,
Han Z,
Sun S,
Huang Z. The existence and uniquenessof solutions to boundary value problems of fractional difference equations. Mathematical Science 2012; 6: 7.
10.1186/2251-7456-6-7 Google Scholar
- 7 Bastos NRO, Ferreira RAC, Torres DFM. Discrete-time fractional variational problems. Signal Process 2011; 91: 513–524.
- 8 Ferreira RAC. A discrete fractional Gronwall inequality. Proc. Amer. Math. Soc, Vol. 140, Rhode Island, USA, 2012, 1605–1612.
- 9 Ferreira RAC. Existence and uniqueness of solution to some discrete fractional boundary value problems of order less than one. Journal of Difference Equations and Applications 2013; 19: 712–718.
- 10 Ferreira RAC, Goodrich CS. Positive solution for a discrete fractional periodic boundary value problem. Dynamics of Continuous Discrete and Impulsive Systems-Series A-Mathematical Analysis 2012; 19: 545–557.
- 11 Ferreira RAC, Torres DFM. Fractional h-difference equations arising from the calculus of variations. Applicable Analysis and Discrete Mathematics 2011; 5: 110–121.
- 12 Goodrich CS. Continuity of solutions to discrete fractional initial value problems. Computers & Mathematics with Applications 2010; 59: 3489–3499.
- 13 Goodrich CS. Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions. Computers & Mathematics with Applications 2011; 61: 191–202.
- 14 Goodrich CS. Existence of a positive solution to a system of discrete fractional boundary value problems. Applied Mathematics and Computation 2011; 217: 4740–4753.
- 15 Goodrich CS. On discrete sequential fractional boundary value problems. Journal of Mathematical Analysis and Applications 2012; 385: 111–124.
- 16 Goodrich CS. On a discrete fractional three-point boundary value problem. Journal of Difference Equations and Applications 2012; 18: 397–415.
- 17 Goodrich CS. On a first-order semipositone discrete fractional boundary value problem. Arch. Math. (Basel) 2012; 99: 509–518.
- 18 Goodrich CS. On semipositone discrete fractional boundary value problems with nonlocal boundary conditions. Journal of Difference Equations and Applications 2013; 19: 1758–1780.
- 19 Dahal R, Duncan D, Goodrich CS. Systems of semipositone discrete fractional boundary value problems. Journal of Difference Equations and Applications 2014; 20: 473–491.
- 20
Holm M. Sum and difference compositions in discrete fractional calculus. CUBO 2011; 13: 153–184.
10.4067/S0719-06462011000300009 Google Scholar
