Mathematical Methods in the Applied Sciences

Volume 38, Issue 8 pp. 1557-1567

Research Article

Asymptotic behavior for the singularly perturbed damped Boussinesq equation

Ke Li,

Corresponding Author

Ke Li

School of Mathematics and Statistics, ZhengZhou University, No.100 Science Road, Zhengzhou 450001, China

Correspondence to: Ke Li, School of Mathematics and Statistics, Zhengzhou University, China.

E-mail: [email protected]

Search for more papers by this author

Zhijian Yang,

Zhijian Yang

School of Mathematics and Statistics, ZhengZhou University, No.100 Science Road, Zhengzhou 450001, China

Search for more papers by this author

Ke Li,

Corresponding Author

Ke Li

School of Mathematics and Statistics, ZhengZhou University, No.100 Science Road, Zhengzhou 450001, China

Correspondence to: Ke Li, School of Mathematics and Statistics, Zhengzhou University, China.

E-mail: [email protected]

Search for more papers by this author

Zhijian Yang,

Zhijian Yang

School of Mathematics and Statistics, ZhengZhou University, No.100 Science Road, Zhengzhou 450001, China

Search for more papers by this author

First published: 13 May 2014

https://doi.org/10.1002/mma.3167

Citations: 3

Share a link

Email
Wechat
Bluesky

Abstract

This work is focused on the long-time behavior of solutions to the singularly perturbed damped Boussinesq equation in a 3D case

$urn:x-wiley:1704214:media:mma3167:mma3167-math-0001$

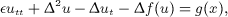
where ε > 0 is small enough. Without any growth restrictions on the nonlinearity f(u), we establish in an appropriate bounded phase space a finite dimensional global attractor as well as an exponential attractor of optimal regularity. The key step is the estimate of the difference between the solutions of the damped Boussinesq equation and the corresponding pseudo-parabolic equation.Copyright © 2014 John Wiley & Sons, Ltd.

References

1 Boussinesq J. Théorie des ondes et des remous qui se propagent le long d'un canal rectangulaire horizontal en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. Journal de Mathématiques Pures et Appliquées 1872; 17(2): 55–108.
Google Scholar
2 Guenther RB, Lee JW. Partial Differential Equations of Mathematical Physics and Integral Equations. Prentice Hall: New Jersey, 1988.
Google Scholar
3 Lagnese JE, Leugering G, Schmidt EJPG. Modeling, Analysis and Control of Dynamic Elastic Multi-Link Structures. Birkhäuser: Boston, 1994.
10.1007/978-1-4612-0273-8
Web of Science® Google Scholar
4 Lai SY. Different physical structures of solutions for a generalized Boussinesq wave equation. Journal of Computational and Applied Mathematics 2009; 231: 311–318.
10.1016/j.cam.2009.02.025
Web of Science® Google Scholar
5 Qin YM, Yang XG, Wang YZ, Liu X. Blow-up criteria of smooth solutions to the 3D Boussinesq equations. Mathematical Methods in the Applied Sciences 2012; 35: 278–285.
10.1002/mma.1558
Web of Science® Google Scholar
6 Wang SB, Chen GW. The Cauchy problem for the generalized IMBq equation in W^s,p(Rⁿ). Journal of Mathematical Analysis and Applications 2002; 266: 38–54.
10.1006/jmaa.2001.7670
Web of Science® Google Scholar
7 Wang SB, Xu HY. On the asymptotic behavior of solution for the generalized IBq equation with hydrodynamical damped term. Journal of Differential Equations 2012; 252: 4243–4258.
10.1016/j.jde.2011.12.016
Web of Science® Google Scholar
8 Wang Y, Mu CL, Wu Y. Decay and scattering of solutions for a generalized Boussinesq equation. Journal of Differential Equations 2009; 247: 2380–2394.
10.1016/j.jde.2009.07.022
Web of Science® Google Scholar
9 Yang ZJ, Guo BL. Cauchy problem for the multi-dimensional Boussinesq type equation. Journal of Mathematical Analysis and Applications 2008; 340: 64–80.
10.1016/j.jmaa.2007.08.017
Web of Science® Google Scholar
10 Liu Y. Instability of solitary waves for generalized Boussinesq equations. Journal of Dynamics and Differential Equations 1993; 5: 537–558.
10.1007/BF01053535
Google Scholar
11 Liu Y. Existence and blow up of a nonlinear Pochhammer–Chree equation. Indiana University Mathematics Journal 1996; 45: 797–816.
Web of Science® Google Scholar
12 Liu Y. Decay and scattering of small solutions of a generalized Boussinesq equation. Journal of Functional Analysis 1997; 147: 51–68.
10.1006/jfan.1996.3052
Web of Science® Google Scholar
13 Liu Y. Instability and blow-up of solutions to a generalized Boussinesq equation. SIAM Journal on Mathematical Analysis 1995; 26: 1527–1546.
10.1137/S0036141093258094
Web of Science® Google Scholar
14 Yang ZJ. Longtime dynamics of the damped Boussinesq equation. Journal of Mathematical Analysis and Applications 2013; 399: 180–190.
10.1016/j.jmaa.2012.09.042
Web of Science® Google Scholar
15 Willett D, Wong JSW. On the discrete analogues of some generalizations of Gronwall's inequality. Monatshefte für Mathematik 1964; 69: 362–367.
10.1007/BF01297622
Google Scholar
16 Zelik S. The attractor for a nonlinear reaction-diffusion system with a supercritical nonlinearity and it's dimension. Rendiconti della Accademia Nazionale delle Scienze Detta Dei XL. Serie V. Memorie di Matemtica 2000; 24: 1–25.
Google Scholar
17 Chueshov I, Lasiecka I. Von Karman Evolution Equations. Spring: New York, 2010.
10.1007/978-0-387-87712-9
Web of Science® Google Scholar

Citing Literature

Volume38, Issue8

30 May 2015

Pages 1557-1567

Asymptotic behavior for the singularly perturbed damped Boussinesq equation

Abstract

References

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Asymptotic behavior for the singularly perturbed damped Boussinesq equation

Abstract

References

Citing Literature

References

Related

Information