Infinitely many homoclinic solutions for a class of damped vibration problems
Corresponding Author
Peng Chen
College of Science, China Three Gorges University, Yichang, Hubei 443002, China
Correspondence to: Peng Chen, College of Science, China Three Gorges University, Yichang, Hubei 443002, China.
E-mail: [email protected]
Search for more papers by this authorX. H. Tang
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, China
Search for more papers by this authorCorresponding Author
Peng Chen
College of Science, China Three Gorges University, Yichang, Hubei 443002, China
Correspondence to: Peng Chen, College of Science, China Three Gorges University, Yichang, Hubei 443002, China.
E-mail: [email protected]
Search for more papers by this authorX. H. Tang
School of Mathematics and Statistics, Central South University, Changsha, Hunan 410083, China
Search for more papers by this authorAbstract
In this paper, we deal with the existence of infinitely many homoclinic solutions for the damped vibration problems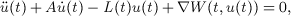 
where A is an antisymmetry N × N constant matrix, we establish some new existence results to guarantee that the above system has infinitely many homoclinic solutions under more relaxed assumptions on W(t,x), which satisfies a kind of new subquadratic condition by using fountain theorem. Recent results in the literature are generalized and significantly improved. Copyright © 2013 John Wiley & Sons, Ltd.
References
- 1 Ding Y. Existence and multiplicity results for homoclinic solutions to a class of Hamiltonian systems. Nonlinear Analysis 1995; 25: 1095–1113.
- 2 Daouas A, Moulahi A. Existence of infinitely many homoclinic orbits for second-order systems involving Hamiltonian-tye equations, Electron. Journal of Differential Equations 2013; 2013(11): 1–16.
- 3
Mawhin J,
Willem M. Critical Point Theory and Hamiltonian Systems in: Applied Mathematical Sciences, Vol. 74. Springer-Verlag: New York, 1989.
10.1007/978-1-4757-2061-7 Google Scholar
- 4 Izydorek M, Janczewska J. Homoclinic solutions for a class of second order Hamiltonian systems. Journal of Differential Equations 2005; 219(2): 375–389.
- 5 Lv Y, Tang C. Existence of even homoclinic orbits for second-order Hamiltonian systems. Nonlinear Analysis 2007; 67: 2189–2198.
- 6 Lv X, Lu S, Yan P. Existence of homoclinic solutions for a class of second order Hamiltonian systems. Nonlinear Analysis 2010; 72: 390–398.
- 7 Ou ZQ, Tang CL. Existence of homoclinic orbits for the second order Hamiltonian systems. Journal of Mathematical Analysis and Applications 2004; 291(1): 203–213.
- 8
Rabinowitz PH. Homoclinic orbits for a class of Hamiltonian systems. Proceedings of Royal Society of Edinburgh Section A 1990; 114(1-2): 33–38.
10.1017/S0308210500024240 Google Scholar
- 9 Salvatore A. Homoclinic orbits for a special class of nonautonomous Hamiltonian systems. Proceedings of the Second World Congress of Nonlinear Analysis. Part 8 (Athens, 1996), Nonlinear Anal. 1997; 30(8): 4849–4857.
- 10 Szulkin A, Zou W. Homoclinic orbits for asymptotically linear Hamiltonian systems. Journal of Functional Analysis 2001; 187(1): 25–41.
- 11 Sun J, Chen H, Nieto JJ. Homoclinic solutions for a class of subquadratic second-order Hamiltonian systems. Journal of Mathematical Analysis and Applications 2011; 373: 20–29.
- 12 Tang XH, Lin XY. Infinitely many homoclinic orbits for Hamiltonian systems with indefinite sign subquadratic potentials. Nonlinear Analysis 2011; 74(17): 6314–6325.
- 13 Wang J, Zhang F, Xu J. Existence and multiplicity of homoclinic orbits for the second order Hamiltonian systems. Journal of Mathematical Analysis and Applications 2010; 366: 569–581.
- 14 Wei J, Wang J. Infinitely many homoclinic orbits for second order Hamiltonian systems with general potenial. Journal of Mathematical Analysis and Applications 2010; 366: 694–699.
- 15 Yang L, Chen H, Sun J. Infinitely many homoclinic solutions for some second order Hamiltonian systems. Nonlinear Analysis 2011; 74: 6459–6468.
- 16 Yang J, Zhang FB. Infinitely many homoclinic orbits for the second-order Hamiltonian systems with super-quadratic potentials. Nonlinear Analysis 2009; RWA 10: 1417–1423.
- 17 Zhang Q, Liu C. Infinitely many homoclinic solutions for second order Hamiltonian systems. Nonlinear Analysis 2010; 72: 894–903.
- 18 Zhang Z, Yuan R. Homoclinic solutions for some second-order nonautonomous systems. Nonlinear Analysis 2009; 71: 5790–5798.
- 19 Zhang Z, Yuan R. Homoclinic solutions for a class of asymptotically quadratic Hamiltonian systems. Nonlinear Analysis 2010; RWA 11: 4185–4193.
- 20 Zou W. Variant fountain theorems and their applications. Manuscripta Mathematica 2001; 104: 343–358.
- 21 Zou W, Li SJ. Infinitely many homoclinic orbits for the second order Hamiltonian systems. Applied Mathematics Letters 2003; 16: 1283–1287.
- 22 Wu X, Zhang W. Existence and multiplicity of homoclinic solutions for a class of damped vibration problems. Nonlinear Analysis 2011; 74: 4392–4398.
- 23 Zhu W. Existence of homoclinic solutions for a class of second order systems. Nonlinear Analysis 2012; 75: 2455–2463.
