A Navier–Stokes–Voight model with memory
Corresponding Author
Ciprian G. Gal
Department of Mathematics, Florida International University, DM413B, University Park, Miami, Florida, 33199 USA
Correspondence to: Ciprian G. Gal, Department of Mathematics, Florida International University, DM413B, University Park, Miami, Florida 33199, USA.
E-mail: [email protected]
Search for more papers by this authorT. Tachim Medjo
Department of Mathematics, Florida International University, DM413B, University Park, Miami, Florida, 33199 USA
Search for more papers by this authorCorresponding Author
Ciprian G. Gal
Department of Mathematics, Florida International University, DM413B, University Park, Miami, Florida, 33199 USA
Correspondence to: Ciprian G. Gal, Department of Mathematics, Florida International University, DM413B, University Park, Miami, Florida 33199, USA.
E-mail: [email protected]
Search for more papers by this authorT. Tachim Medjo
Department of Mathematics, Florida International University, DM413B, University Park, Miami, Florida, 33199 USA
Search for more papers by this authorAbstract
In this article, we consider a three-dimensional Navier–Stokes–Voight model with memory where relaxation effects are described through a distributed delay. We prove the existence of uniform global attractors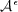 
, where ϵ ∈ (0,1) is the scaling parameter in the memory kernel. Furthermore, we prove that the model converges to the classical three-dimensional Navier–Stokes–Voight system in an appropriate sense as ϵ → 0. In particular, we construct a family of exponential attractors Ξϵ that is robust as ϵ → 0. Copyright © 2013 John Wiley & Sons, Ltd.
References
- 1
Thompson W. On the elasticity and viscosity of metals. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 1865; 14: 289–297.
10.1098/rspl.1865.0052 Google Scholar
- 2
Voight W. Ueber innere Reibung fester KÄorper, insbesondere der Metalle. Annalen der Physik 1892; 283: 671–693.
10.1002/andp.18922831210 Google Scholar
- 3 Oskolkov AP. The uniqueness and solvability in the large of boundary value problems for the equations of motion of aqueous solutions of polymers. Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta imeni V. A. Steklova Akademii Nauk SSSR (LOMI) 1973; 38: 98–136.
- 4 Oskolkov AP. On the theory of Voight fluids. Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta imeni V. A. Steklova Akademii Nauk SSSR (LOMI) 1980; 96: 233–236.
- 5 Böhm M. On Navier–Stokes and Kelvin–V oigt equations in three dimensions in interpolation spaces. Mathematische Nachrichten 1992; 155: 151–165.
- 6 Larios A, Titi ES. On the higher-order global regularity of the inviscid Voigt-regularization of three-dimensional hydrodynamic models. Discrete and Continuous Dynamical Systems - Series B 2010; 14(2): 603–627.
- 7 Levant B, Ramos F, Titi ES. On the statistical properties of the 3D incompressible Navier–Stokes–Voigt model. Communications in Mathematical Sciences 2010; 8(1): 277–293.
- 8 Kalantarov V, Levant B, Titi ES. Gevrey regularity of the global attractor of the 3D Navier–Stokes–Voight equations. Journal of Nonlinear Science 2009; 19: 133–152.
- 9 Kalantarov V, Titi ES. Global attractors and determining modes for the 3D Navier–Stokes–Voight equations. Chinese Annals of Mathematics B 2009; 30(6): 697–714.
- 10 Ramos F, Titi ES. Invariant measure for the 3 D Navier–Stokes–Voigt equations and their Navier–Stokes limit. Discrete and Continuous Dynamical Systems - Series A 2010; 28(1): 375–403.
- 11
Oskolkov AP. Boundary value problems of mathematical physics and related questions in the theory of functions, 14. Zapiski Nauchnykh Seminarov Leningradskogo Otdeleniya Matematicheskogo Instituta imeni V. A. Steklova Akademii Nauk SSSR (LOMI) 1982; 115: 191–202, 310; translated in: Theory of nonstationary flows of Kelvin–Voight fluids, Journal of Mathematical Sciences 28 (5), 751-758, DOI: 10.1007/BF02112340.
10.1007/BF02112340 Google Scholar
- 12 Oldroyd JG. Second-order Effects in Elasticity. Plasticity, and Fluid Dynamics: Oxford, 1963.
- 13 Wilkinson W. L. Non-Newtonian Fluids. Pergamon Press: New York, 1960.
- 14 Gatti S, Giorgi C, Pata V. Navier–Stokes limit of Jeffreys type flows. Physica D. Nonlinear Phenomena 2005; 203: 55–79.
- 15
Dafermos CM. Asymptotic stability in viscoelasticity. Archive for Rational Mechanics and Analysis 1970; 37: 554–569.
10.1007/BF00251609 Google Scholar
- 16 Turbin MV. On the correct formulation of initial-boundary value problems for the generalized Kelvin–Voight model. (Russian) Izvestiya Vysshikh Uchebnykh Zavedeniĭ. Matematika. Kazanskiĭ Gosudarstvennyĭ Universitet 2006; 3: 50–58; translation in Russian Mathematics (Izvestiya VUZ. Matematika) 50 (2006), no. 3, 47–55.
- 17
Ebrahimi MA,
Holst M,
Lunasin E. The Navier–Stokes–Voight model for image inpainting. IMA Journal of Applied Mathematics 2012. DOI: 10.1093/imamat/hxr069.
10.1093/imamat/hxr069 Google Scholar
- 18
Constantin P,
Foias C. Navier–Stokes equations. Chicago Lectures in Mathematics. University of Chicago Press: Chicago, IL, 1988.
10.7208/chicago/9780226764320.001.0001 Google Scholar
- 19 Temam R. Infinite Dimensional Dynamical Systems in Mechanics and Physics, 2nd ed., Vol. 68. Appl. Math. Sci., Springer–Verlag: New York, 1988.
- 20 Gatti S, Grasselli M, Miraville A, Pata V. Memory relaxation of first order evolution equations. Nonlinearity 2005; 18(4): 1859–1883.
- 21 Grasselli M, Pata V. Uniform attractors of nonautonomous dynamical systems with memory. In Progress in Nonlinear Differential Equations and Their Applications, P, Vol. 50. Birkhauser Verlag: Basel/Switzerland, 2002.
- 22 Kloeden PE, Real J, Sun C. Robust exponential attractors for non-autonomous equations with memory. Communications on Pure and Applied Analysis 2011; 10(3): 885–915.
- 23 Yue G, Zhong C. Attractors for autonomous and nonautonomous 3D Navier–Stoke–Voight equations. Discrete and Continuous Dynamical Systems - Series B 2011; 16(3): 985–1002.
