Research Article
Multiple solutions for a semilinear elliptic system in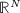 
Gongbao Li,
Chunhua Wang,
Gongbao Li
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China
Search for more papers by this authorCorresponding Author
Chunhua Wang
Central Normal University, Wuhan, China
Correspondence to: ChunhuaWang, School ofMathematics and Statistics, Central China Normal University,Wuhan 430079, China.
E-mail: [email protected]
Search for more papers by this authorGongbao Li,
Chunhua Wang,
Gongbao Li
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, China
Search for more papers by this authorCorresponding Author
Chunhua Wang
Central Normal University, Wuhan, China
Correspondence to: ChunhuaWang, School ofMathematics and Statistics, Central China Normal University,Wuhan 430079, China.
E-mail: [email protected]
Search for more papers by this authorAbstract
In this paper, we study the following semilinear elliptic system
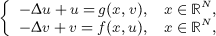
References
- 1 Benci V, Rabinowitz PH. Critical point theorems for indefinite functionals. Inventiones Mathematicae 1979; 52: 241–273.
- 2
de Figueiredo DG,
Felmer PL. On superquadratic elliptic systems. Transactions of the American Mathematical Society 1994; 343: 99–116.
10.1090/S0002-9947-1994-1214781-2 Google Scholar
- 3 Hulshof J, Van der Vorst RCAM. Differential systems with strongly indefinite variational structure. Journal of Functional Analysis 1993; 114: 32–58.
- 4
Kryszewski W,
Szulkin A. Generalized linking theorem with an application to semilinear Schrödinger equation. Advances in Differential Equations 1998; 3: 441–472.
10.57262/ade/1366399849 Google Scholar
- 5 de Figueiredo DG, do Ó JM, Ruf B. An Orlicz-space approach to superlinear elliptic systems. Journal of Functional Analysis 2005; 224: 471–496.
- 6 de Figueiredo DG, Yang JF. Decay, symmetry and existence of solutions of semilinear elliptic systems. Nonlinear Analysis: Theory, Methods & Applications 1998; 33: 211–234.
- 7
Sirakov B. On the existence of solutions of Hamiltonian elliptic systems in
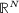. Advances in Differential Equations 2000; 5: 1445–1464.
- 8 Ding YH, Li SJ. Existence of entire solutions for some elliptic systems. Bulletin of the Australian Mathematical Society 1994; 50: 501–519.
- 9 Reed M, Simon B. Methods of Modern Mathematical Physics. I. Functional analysis, 2nd ed. Academic Press Inc.: New York, 1980.
- 10 Li GB, Yang JF. Asymptotically linear elliptic systems. Communications in Partial Differential Equations 2004; 29: 925–954.
- 11
Li GB,
Wang CH. The existence of nontrivial solutions to a semilinear elliptic system on
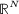without the Ambrosetti–Rabinowitz condition. Acta Mathematica Scientia Series B English Edition 2010; 30: 1917–1936.
- 12 Ávila AI, Yang JF. On the existence and shape of least energy solutions for some elliptic systems. Journal of Differential Equations 2003; 191: 348–376.
- 13 Ávila AI, Yang JF. Multiple solutions of nonlinear elliptic systems. Nonlinear Differential Equations and Applications 2005; 12: 459–479.
- 14 Alves CO, Carriáo PC, Miyagaki OH. Multi-bump homoclinic orbits for a class of Hamiltonian systems with superquadratic potential. Houston Journal of Mathematics 2010; 36: 859–877.
- 15
Yang JF. Nontrivial solutions of semilinear elliptic systems in
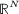. Electronic Journal of Differential Equations Conference 2000; 6: 343–357.
- 16 Pistoia A, Ramos M. Locating the peaks of the least energy solutions to an elliptic system with Dirichlet boundary conditions. Nonlinear Differential Equations and Applications 2008; 15: 1–23.
- 17 Pistoia A, Ramos M. Locating the peaks of the least energy solutions to an elliptic system with Neumann boundary conditions. Journal of Differential Equations 2004; 201: 160–176.
- 18 Zhao FK, Zhao LG, Ding YH. Multiple solutions for asymptotically linear elliptic systems. Nonlinear Differential Equations and Applications 2008; 15: 673–688.
- 19 Bartsch T, Ding YH. Deformation theorems on non-metrizable vector spaces and applications to critical point theory. Mathematische Nachrichten 2006; 279: 1267–1288.
- 20 Coti Zelati V, Rabinowitz PH. Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. Journal of the American Mathematical Society 1991; 4: 693–727.
- 21
Coti Zelati V,
Rabinowitz PH. Homoclinic type solutions for a semilinear elliptic PDE on
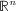. Communications on Pure and Applied Mathematics 1992; 45: 1217–1269.
- 22 Jeanjean L. On the existence of bounded Palais–Smale sequences and application to a Landesmann-Laze type problem. Proceedings of the Royal Society of Edinburgh, Section: A Mathematics 1999; 129: 787–809.
- 23 Bartsch T, Clapp M. Critical point theory for indefinite functionals with symmetries. Journal of Functional Analysis 1996; 138: 107–136.
- 24 Bartsch T, de Figueiredo DG. Infinitely many solutions of nonlinear elliptic systems. Topics in nonlinear analysis. In Progr. Nonlinear Differential Equations Appl., Vol. 35. Birkhäuser: Basel, 1999; 51–67.
- 25 Kryszewski W, Szulkin A. An infinite-dimensional Morse theory with applications. Transactions of the American Mathematical Society 1997; 349: 3181–3234.
- 26 Li GB, Szulkin A. An asymptotically periodic Schrödinger equation with indefinite linear part. Communications in Contemporary Mathematics 2002; 4: 763–776.
- 27 Ackermann N. A nonlinear superposition principle and multibump solutions of periodic Schrödinger equations. Journal of Functional Analysis 2006; 234: 277–320.
- 28 Ackermann N. On a periodic Schrödinger equation with nonlocal superlinear part. Mathematische Zeitschrift 2004; 248: 423–443.
- 29 Ding YH, Jeanjean L. Homoclinic orbits for a nonperiodic Hamiltonian system. Journal of Differential Equations 2007; 237: 473–490.
- 30 Séré E. Existence of infinitely many homoclinic orbits in Hamiltonian systems. Mathematische Zeitschrift 1992; 209: 27–42.
- 31 Willem M. Minimax theorems. In Progress in Nonlinear Differential Equations and their Applications, Vol. 24. Birkhäuser Boston, Inc.: Boston, MA, 1996; 16.
