Original Paper
Strong convergence of two-dimensional Vilenkin-Fourier series
Nacima Memić,
Ilona Simon,
George Tephnadze,
Nacima Memić
Department of Mathematics, University of Sarajevo, Zmaja od Bosne 33-35, Sarajevo, Bosnia and Herzegovina
Search for more papers by this authorIlona Simon
Institute of Mathematics and Informatics, University of Pėcs, H-7624 Pėcs, Ifjúsàg u. 6., Hungary
Search for more papers by this authorCorresponding Author
George Tephnadze
Department of Mathematics, Faculty of Exact and Natural Sciences, Tbilisi State University, Chavchavadze str. 1, Tbilisi, 0128 Georgia
Department of Engineering Sciences and Mathematics, Luleå University of Technology, SE-971 87, Luleå, Sweden
Corresponding author: e-mail: [email protected], Phone: +995 598 405 165Search for more papers by this authorNacima Memić,
Ilona Simon,
George Tephnadze,
Nacima Memić
Department of Mathematics, University of Sarajevo, Zmaja od Bosne 33-35, Sarajevo, Bosnia and Herzegovina
Search for more papers by this authorIlona Simon
Institute of Mathematics and Informatics, University of Pėcs, H-7624 Pėcs, Ifjúsàg u. 6., Hungary
Search for more papers by this authorCorresponding Author
George Tephnadze
Department of Mathematics, Faculty of Exact and Natural Sciences, Tbilisi State University, Chavchavadze str. 1, Tbilisi, 0128 Georgia
Department of Engineering Sciences and Mathematics, Luleå University of Technology, SE-971 87, Luleå, Sweden
Corresponding author: e-mail: [email protected], Phone: +995 598 405 165Search for more papers by this authorAbstract
We prove that certain means of the quadratical partial sums of the two-dimensional Vilenkin-Fourier series are uniformly bounded operators from the Hardy space 
to the space 
for 
We also prove that the sequence in the denominator cannot be improved.
References
- 1G. N. Agaev, N. Ya. Vilenkin, G. M. Dzhafarly, and A. I. Rubinshtein, Multiplicative Systems of Functions and Harmonic Analysis on Zero-Dimensional Groups, Baku, Ehim, 1981 (in Russian).
- 2I. Blahota, On a norm inequality with respect to Vilenkin-like systems, Acta Math. Hungar. 89(1–2), 15–27 (2000).
- 3I. Blahota, Relation between Dirichlet kernels with respect to Vilenkin-like systems, Acta Academiae Paedagogicae Agriensis XXII, 109–114 (1994).
- 4I. Blahota and G. Tephnadze, Strong convergence theorem for Vilenkin-Fejér means, Publ. Math. Debrecen 85(1–2), 181–196 (2014).
- 5I. Blahota, G. Tephnadze, and R. Toledo, Strong convergence theorem of
-means with respect to the Walsh system, Tohoku Math. J. (2) (to appear).
- 6G. Gát, Inverstigations of certain operators with respect to the Vilenkin sistem, Acta Math. Hungar. 61, 131–149 (1993).
- 7G. Gát, U. Goginava, and K. Nagy, On the Marcinkiewicz-Fejér means of double Fourier series with respect to the Walsh-Kaczmarz system, Stud. Sci. Math. Hungar. 46(3), 399–421 (2009).
- 8G. Gát, U. Goginava, and G. Tkebuchava, Convergence in measure of logarithmic means of quadratical partial sums of double Walsh-Fourier series, J. Math. Anal. Appl. 323(1), 535–549 (2006).
- 9U. Goginava, The weak type inequality for the maximal operator of the Marcinkiewicz-Fejér means of the two-dimensional Walsh-Fourier series, J. Approx. Theory 154(2), 161–180 (2008).
- 10U. Goginava, The weak type inequality for the maximal operator of the
means of the two-dimensional Walsh-Fourier series, Anal. Math. 36(1), 1–31 (2010).
- 11U. Goginava, Almost everywhere convergence of
-means of cubical partial sums of d-dimensional Walsh-Fourier series, J. Approx. Theory 141(1), 8–28 (2006).
- 12U. Goginava and L. D. Gogoladze, Strong approximation by Marccinkiewicz means of two-dimensional Walsh-Fourier series, Constr. Approx. 35(1), 1–19 (2012).
- 13U. Goginava and L. D. Gogoladze, Strong convergence of cubic partial sums of two-dimensional Walsh-Fourier series, In: Constructive Theory of Functions, Sozopol 2010: In memory of Borislav Bojanov. Prof. (Marin Drinov Academic Publishing House, Sofia, 2012), pp. 108-117.
- 14L. D. Gogoladze, On the strong summability of Fourier series, Bull Acad. Sci. Georgian SSR 52(2), 287–292 (1968).
- 15B. Golubov, A. Efimov, and V. Skvortsov, Walsh Series and Transformations (Dordrecht, Boston, London, 1991). Kluwer Acad. Publ; 1991.
10.1007/978-94-011-3288-6 Google Scholar
- 16S. F. Lukomskii, Lebesgue constants for characters of the compact zero-dimensional Abelian group, East J. Approx. 15(2), 219–231 (2009).
- 17K. Nagy and G. Tephnadze, On the Walsh-Marcinkiewicz means on the Hardy space, Cent. Eur. J. Math., DOI: 10.2478/s11533-014-0406-1.
- 18K. Nagy and G. Tephnadze, Strong convergence theorem for Walsh-Marcinkiewicz means, Math. Inequal. Appl. (to appear).
- 19K. Nagy and G. Tephnadze, Kaczmarz-Marcinkiewicz means and Hardy spaces, J. Funct. Spaces, (in press).
- 20F. Schipp, W. R. Wade, P. Simon, and J. Pál, Walsh Series, An Introduction to Dyadic Harmonic Analysis (Adam Hilger, Bristol, New York, 1990).
- 21P. Simon, Strong convergence of certain means with respect to the Walsh-Fourier series, Acta Math. Hungar. 49, 425–431 (1987).
- 22P. Simon, Strong convergence theorem for Vilenkin-Fourier series, J. Math. Anal. Appl. 245, 52–68 (2000).
- 23B. Smith, A strong convergence theorem for
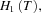in Lecture Notes in Mathematics, Vol. 995 (Springer, Berlin, 1994), pp. 169–173.
- 24G. Tephnadze, Strong convergence of two-dimensional Walsh-Fourier series, Ukrainian Math. J. (UMJ) 65(N6), 914–926 (2013).
- 25G. Tephnadze, A note on the strong convergence of two-dimensional Walsh-Fourier series, Proceedings of A. Razmadze Mathematical Institute 162, 93–97 (2013).
- 26G. Tephnadze, On the partial sums of Vilenkin-Fourier series, J. Contemp. Math. Anal. 49(1), 23–32 (2014).
- 27G. Tephnadze, A note of the Fourier coefficients and partial sums of Vilenkin-Fourier series, Acta Math. Acad. Paedagog. Nyiregyhazie. (N. S.) (AMAPN) 28, 167–176 (2012).
- 28N. Ya. Vilenkin, On a class of complete orthonormal systems, Izv. Akad. Nauk. U.S.S.R., Ser. Mat. 11, 363–400 (1947).
- 29F. Weisz, Martingale Hardy Spaces and their Applications in Fourier Analysis (Springer, Berlin - Heidelberg - New York, 1994).
10.1007/BFb0073448 Google Scholar
- 30F. Weisz, Summability of Multi-Dimensional Fourier Series and Hardy Space (Kluwer Academic, Dordrecht, Boston, London, 2002).
10.1007/978-94-017-3183-6 Google Scholar
- 31F. Weisz, Strong convergence theorems for two-parameter Walsh-Fourier and trigonometric-Fourier series (English) Stud. Math. 117(2), 173–194 (1996).
