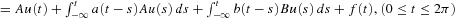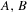We study the well-posedness of the second order degenerate differential equations with infinite delay: $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0001$ $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0002$ with periodic boundary conditions $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0003$ , where $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0004$ and M are closed linear operators in a Banach space satisfying $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0005$ , $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0006$ . Using operator-valued Fourier multiplier techniques, we give necessary and sufficient conditions for the well-posedness of this problem in Lebesgue-Bochner spaces $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0007$ , periodic Besov spaces $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0008$ and periodic Triebel-Lizorkin spaces $urn:x-wiley:0025584X:media:mana201400112:mana201400112-math-0009$ .

References

1W. Arendt, C. Batty, and S. Bu, Fourier multipliers for Hölder continuous functions and maximal regularity, Studia Math. 160, 23–51 (2004).
10.4064/sm160-1-2
Web of Science® Google Scholar
2W. Arendt, C. Batty, M. Hieber, and F. Neubrander, Vector-valued Laplace Transforms and Cauchy Problems (Birkhäuser, Basel, 2001).
10.1007/978-3-0348-5075-9
Google Scholar
3W. Arendt and S. Bu, The operator-valued Marcinkiewicz multiplier theorem and maximal regularity, Math. Z. 240, 311–343 (2002).
10.1007/s002090100384
Web of Science® Google Scholar
4W. Arendt and S. Bu, Operator-valued Fourier multipliers on periodic Besov spaces and applications, Proc. Edinb. Math. Soc. (2) 47(1), 15–33 (2004).
10.1017/S0013091502000378
Web of Science® Google Scholar
5S. Bu, Well-posedness of second order degenerate differential equations in vector-valued function spaces, Studia Math. 214, 1–16 (2013).
10.4064/sm214-1-1
Web of Science® Google Scholar
6S. Bu, Well-posedness of degenerate differential equations in Hölder continuous function spaces, Front. Math. China 10(2), 239–248 (2015).
10.1007/s11464-014-0368-4
Web of Science® Google Scholar
7S. Bu and J. Kim, Operator-valued Fourier multipliers on periodic Triebel spaces, Acta Math. Sin. (Engl. Ser.) 21(5), 1049–1056 (2005).
10.1007/s10114-004-0453-9
Web of Science® Google Scholar
8A. Favini and A. Yagi, Degenerate Differential Equations in Banach Spaces, Pure and Applied Mathematics 215 (Dekker, New York, Basel, Hong Kong, 1999).
Google Scholar
9V. Keyantuo and C. Lizama, Fourier multipliers and integro-differential equations in Banach spaces, J. London Math. Soc. (2) 69(3), 737–750 (2004).
10.1112/S0024610704005198
Web of Science® Google Scholar
10V. Keyantuo and C. Lizama, Maximal regularity for a class of integro-differential equations with infinite delay in Banach spaces, Studia Math. 168(1), 25–50 (2005).
10.4064/sm168-1-3
Web of Science® Google Scholar
11V. Keyantuo and C. Lizama, Periodic solutions of second order differential equations in Banach spaces, Math. Z. 253, 489–514 (2006).
10.1007/s00209-005-0919-1
Web of Science® Google Scholar
12V. Keyantuo, C. Lizama, and V. Poblete, Periodic solutions of integro-differential equations in vector-valued function spaces, J. Differential Equations 246(3), 1007–1037 (2009).
10.1016/j.jde.2008.09.007
Web of Science® Google Scholar
13C. Lizama and R. Ponce, Periodic solutions of degenerate differential equations in vector-valued function spaces, Studia Math. 202(1), 49–63 (2011).
10.4064/sm202-1-3
Web of Science® Google Scholar
14C. Lizama and R. Ponce, Maximal regularity for degenerate differential equations with infinite delay in periodic vector-valued function spaces, Proc. Edinb. Math. Soc. (2) 56, 853–871 (2013).
10.1017/S0013091513000606
Web of Science® Google Scholar
15V. Poblete, Solutions of second-order integro-differential equations on periodic Besov spaces, Proc. Edinb. Math. Soc. (2) 50(2), 477–492 (2007).
10.1017/S0013091505001057
Web of Science® Google Scholar
16R. Ponce, Hölder continuous solutions for Sobolev type differential equations, Math. Nachr. 287(1), 70–78 (2014).
10.1002/mana.201200168
Web of Science® Google Scholar

Citing Literature

Volume289, Issue4

March 2016

Pages 436-451

Well-posedness of second order degenerate integro-differential equations with infinite delay in vector-valued function spaces

Abstract

References

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Well-posedness of second order degenerate integro-differential equations with infinite delay in vector-valued function spaces

Abstract

References

Citing Literature

References

Related

Information