Absolutely continuous spectrum for random Schrödinger operators on the Bethe strip
Corresponding Author
Abel Klein
Department of Mathematics, University of California, Irvine, CA 92697-3875, USA
Abel Klein, Phone: +1(949)824 5817, Fax: +1(949)824 7993
Christian Sadel, Department of Mathematics, University of California, Irvine, CA 92697-3875, USA, Phone: +1(949)824 2280, Fax: +1(949)824 7993.
Search for more papers by this authorCorresponding Author
Christian Sadel
Department of Mathematics, University of California, Irvine, CA 92697-3875, USA
Abel Klein, Phone: +1(949)824 5817, Fax: +1(949)824 7993
Christian Sadel, Department of Mathematics, University of California, Irvine, CA 92697-3875, USA, Phone: +1(949)824 2280, Fax: +1(949)824 7993.
Search for more papers by this authorCorresponding Author
Abel Klein
Department of Mathematics, University of California, Irvine, CA 92697-3875, USA
Abel Klein, Phone: +1(949)824 5817, Fax: +1(949)824 7993
Christian Sadel, Department of Mathematics, University of California, Irvine, CA 92697-3875, USA, Phone: +1(949)824 2280, Fax: +1(949)824 7993.
Search for more papers by this authorCorresponding Author
Christian Sadel
Department of Mathematics, University of California, Irvine, CA 92697-3875, USA
Abel Klein, Phone: +1(949)824 5817, Fax: +1(949)824 7993
Christian Sadel, Department of Mathematics, University of California, Irvine, CA 92697-3875, USA, Phone: +1(949)824 2280, Fax: +1(949)824 7993.
Search for more papers by this authorAbstract
The Bethe strip of width m is the cartesian product \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\mathbb {B}\times \lbrace 1,\ldots ,m\rbrace$\end{document}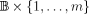
, where \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\mathbb {B}$\end{document}
is the Bethe lattice (Cayley tree). We prove that Anderson models on the Bethe strip have “extended states” for small disorder. More precisely, we consider Anderson-like Hamiltonians \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$H_\lambda =\frac{1}{2} \Delta \otimes 1 + 1 \otimes A\,+\,\lambda \mathcal {V}$\end{document}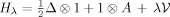
on a Bethe strip with connectivity K ≥ 2, where A is an m × m symmetric matrix, \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$\mathcal {V}$\end{document}
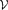is a random matrix potential, and λ is the disorder parameter. Given any closed interval \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$I\subset \big (\!-\!\sqrt{K}+a_{{\rm max}},\sqrt{K}+a_{\rm {min}}\big )$\end{document}
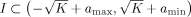, where amin and amax are the smallest and largest eigenvalues of the matrix A, we prove that for λ small the random Schrödinger operator Hλ has purely absolutely continuous spectrum in I with probability one and its integrated density of states is continuously differentiable on the interval I.
References
- 1 E. Abrahams, P. Anderson, D. Licciardello, and T. Ramakrishnan, Scaling theory of localization: absence of quantum diffusion in two dimensions, Phys. Rev. Lett. 42, 673–675 (1979).
- 2 V. Acosta and A. Klein, Analyticity of the density of states in the Anderson model in the Bethe lattice, J. Stat. Phys. 69, 277–305 (1992).
- 3 M. Aizenman, Localization at weak disorder: some elementary bounds, Rev. Math. Phys. 6, 1163–1182 (1994).
- 4 M. Aizenman and S. Molchanov, Localization at large disorder and extreme energies: an elementary derivation, Commun. Math. Phys. 157, 245–278 (1993).
- 5 M. Aizenman, R. Sims, and S. Warzel, Stability of the absolutely continuous spectrum of random Schrödinger operators on tree graphs, Probab. Theory Relat. Fields 136, 363–394 (2006).
- 6 P. Anderson, Absence of diffusion in certain random lattices, Phys. Rev. 109, 1492–1505 (1958).
- 7 F. A. Berezin, The Method of Second Quantization (Academic Press, New York, 1966).
- 8 M. Campanino and A. Klein, A supersymmetric transfer matrix and differentiability of the density of states in the one-dimensional Anderson model, Commun. Math. Phys. 104, 227–241 (1986).
- 9 R. Carmona, A. Klein, and F. Martinelli, Anderson localization for Bernoulli and other singular potentials, Commun. Math. Phys. 108, 41–66 (1987).
- 10
R. Carmona and
J. Lacroix,
Spectral Theory of Random Schrodinger Operators
(Birkhäuser, Boston, MA, 1990).
10.1007/978-1-4612-4488-2 Google Scholar
- 11 F. Delyon, Y. Levy, and B. Souillard, Anderson localization for multidimensional systems at large disorder or low energy, Commun. Math. Phys. 100, 463–470 (1985).
- 12 O. N. Dorokhov, Solvable model of multichannel localization, Phys. Rev. B 37, 10526–10541 (1988).
- 13
H. von Dreifus and
A. Klein,
A new proof of localization in the Anderson tight binding model,
Commun. Math. Phys.
124, 285–299 (1989).
10.1007/BF01219198 Google Scholar
- 14 K. B. Efetov, Supersymmetry and theory of disordered metals, Advances Phys. 32, 53–127 (1983).
- 15 R. Froese, F. Halasan, and D. Hasler, Absolutely continuous spectrum for the Anderson model on a product of a tree with a finite graph, J. Funct. Analysis, arXiv:1008.2949v1 (2010) (to appear).
- 16 R. Froese, D. Hasler, and W. Spitzer, Absolutely continuous spectrum for the Anderson Model on a tree: A geometric proof of Klein's Theorem, Commun. Math. Phys. 269, 239–257 (2007).
- 17 J. Fröhlich, F. Martinelli, E. Scoppola, and T. Spencer, Constructive proof of localization in the Anderson tight binding model, Commun. Math. Phys. 101, 21–46 (1985).
- 18 J. Fröhlich and T. Spencer, Absence of diffusion in the Anderson tight binding model for large disorder or low energy, Commun. Math. Phys. 88, 151–184 (1983).
- 19
Ya. Gol'dsheid,
S. Molchanov, and
L. Pastur,
Pure point spectrum of stochastic one dimensional Schrödinger operators,
Funct. Anal. Appl.
11, 1–10 (1977).
10.1007/BF01135526 Google Scholar
- 20 F. Halasan, Absolutely continuous spectrum for the Anderson model on some tree-like graphs, arXiv:0810.2516v3 (2008).
- 21
T. Kato,
Wave operators and similarity for some non self-adjoint operators,
Math. Ann.
162, 258–279 (1966).
10.1007/BF01360915 Google Scholar
- 22 M. Keller, D. Lenz, and S. Warzel, On the spectral theory of trees with finite cone type, Israel J. Math., arXiv:1001.3600v2 (2011) (to appear).
- 23
A. Klein,
The supersymmetric replica trick and smoothness of the density of states for random Schrodinger operators,
Proc. Symp. Pure Math.
51, 315–331 (1990).
10.1090/pspum/051.1/1077393 Google Scholar
- 24 A. Klein, Localization in the Anderson model with long range hopping, Braz. J. Phys. 23, 363–371 (1993).
- 25 A. Klein, Absolutely continuous spectrum in the Anderson model on the Bethe lattice, Math. Res. Lett. 1, 399–407 (1994).
- 26 A. Klein, Absolutely continuous spectrum in random Schrödinger operators, in: Quantization, Nonlinear Partial Differential Equations, and Operator Algebra (Cambridge, MA, 1994), 139–147, Proc. Sympos. Pure Math. Vol. 59 (American Mathematical Society, Providence, RI, 1996).
- 27 A. Klein, Spreading of wave packets in the Anderson model on the Bethe lattice, Commun. Math. Phys. 177, 755–773 (1996).
- 28 A. Klein, Extended states in the Anderson model on the Bethe lattice, Adv. Math. 133, 163–184 (1998).
- 29 A. Klein, J. Lacroix, and A. Speis, Regularity of the density of states in the Anderson model on a strip for potentials with singular continuous distributions, J. Stat. Phys. 57, 65–88 (1989).
- 30 A. Klein, J. Lacroix, and A. Speis, Localization for the Anderson model on a strip with singular potentials, J. Funct. Anal. 94, 135–155 (1990).
- 31 A. Klein and C. Sadel, Ballistic behavior for random Schrödinger operators on the Bethe strip, J. Spectr. Theory, arXiv:1106.1689v2 (2011) (to appear).
- 32 A. Klein and A. Speis, Smoothness of the density of states in the Anderson model on a one-dimensional strip, Ann. Phys. 183, 352–398 (1988).
- 33 F. Klopp, Weak disorder localization and Lifshitz tails, Commun. Math. Phys. 232, 125–155 (2002).
- 34 H. Kunz and B. Souillard, Sur le spectre des opérateurs aux differences finies aléatoires, Commun. Math. Phys. 78, 201–246 (1980).
- 35 J. Lacroix, Localisation pour l'opérateur de Schrödinger aléatoire dans un ruban, Ann. Inst. Henri Poincaré Ser A 40, 97–116 (1984).
- 36 L. Nirenberg, Topics in Nonlinear Functional Analysis (Courant Institute of Mathematical Sciences, New York, 1974).
- 37
L. Pastur,
Spectra of random selfadjoint operators,
Russ. Math. Surv.
28, 1–67 (1973).
10.1070/RM1973v028n01ABEH001396 Google Scholar
- 38 C. Sadel and H. Schulz-Baldes, Random Dirac operators with time reversal symmetry, Commun. Math. Phys. 295, 209–242 (2010).
- 39 B. Simon and T. Wolff, Singular continuum spectrum under rank one perturbations and localization for random Hamiltonians, Commun. Pure Appl. Math. 39, 75–90 (1986).
- 40 F. Wegner, Disordered systems with n orbitals per site: n = ∞ limit, Phys. Rev. B 19, 783–792 (1979).
- 41 W.-M Wang, Localization and universality of Poisson statistics for the multidimensional Anderson model at weak disorder, Invent. Math. 146, 365–398 (2001).
