Positive solutions for mixed problems of singular fractional differential equations

We investigate the existence of positive solutions to the singular fractional boundary value problem: \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$^c\hspace{-1.0pt}D^{\alpha }u +f(t,u,u^{\prime },^c\hspace{-2.0pt}D^{\mu }u)=0$\end{document}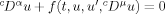, u′(0) = 0, u(1) = 0, where 1 < α < 2, 0 < μ < 1, f is a L^q-Carathéodory function, \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$q > \frac{1}{\alpha -1}$\end{document}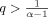, and f(t, x, y, z) may be singular at the value 0 of its space variables x, y, z. Here \documentclass{article}\usepackage{amssymb}\begin{document}\pagestyle{empty}$^c \hspace{-1.0pt}D$\end{document} 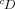stands for the Caputo fractional derivative. The results are based on combining regularization and sequential techniques with a fixed point theorem on cones.