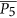Linearly χ-bounding (P6, C4)-free graphs*
*An extended abstract of this paper appeared in the proceedings of WG 2017.
Abstract
Given two graphs 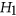 and
and 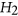 , a graph
, a graph  is
is 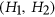 -free if it contains no induced subgraph isomorphic to
-free if it contains no induced subgraph isomorphic to 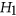 or
or  . Let
. Let 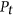 and
and 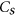 be the path on
be the path on  vertices and the cycle on
vertices and the cycle on 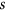 vertices, respectively. In this paper we show that for any
vertices, respectively. In this paper we show that for any 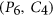 -free graph
-free graph 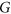 it holds that
it holds that 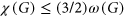 , where
, where 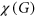 and
and 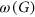 are the chromatic number and clique number of
are the chromatic number and clique number of 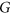 , respectively. Our bound is attained by several graphs, for instance, the 5-cycle, the Petersen graph, the Petersen graph with an additional universal vertex, and all
, respectively. Our bound is attained by several graphs, for instance, the 5-cycle, the Petersen graph, the Petersen graph with an additional universal vertex, and all 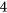 -critical
-critical 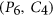 -free graphs other than
-free graphs other than 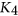 (see Hell and Huang [Discrete Appl. Math. 216 (2017), pp. 211–232]). The new result unifies previously known results on the existence of linear
(see Hell and Huang [Discrete Appl. Math. 216 (2017), pp. 211–232]). The new result unifies previously known results on the existence of linear 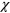 -binding functions for several graph classes. Our proof is based on a novel structure theorem on
-binding functions for several graph classes. Our proof is based on a novel structure theorem on 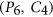 -free graphs that do not contain clique cutsets. Using this structure theorem we also design a polynomial time
-free graphs that do not contain clique cutsets. Using this structure theorem we also design a polynomial time 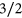 -approximation algorithm for coloring
-approximation algorithm for coloring 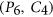 -free graphs. Our algorithm computes a coloring with
-free graphs. Our algorithm computes a coloring with 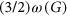 colors for any
colors for any 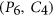 -free graph
-free graph 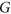 in
in 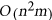 time.
time.



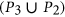 -free graphs, 2016, arXiv:1610.07177v1 [cs.DM].
-free graphs, 2016, arXiv:1610.07177v1 [cs.DM].
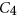 and
and 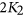
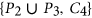 -free graphs
-free graphs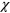 -bound
-bound 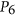 -free graphs
-free graphs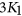 -free graphs
-free graphs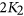 -free graphs-Structural and Combinatorial View, 2016, arXiv:1602.03802v2 [math.CO].
-free graphs-Structural and Combinatorial View, 2016, arXiv:1602.03802v2 [math.CO].
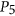 and
and