Induced subgraphs of graphs with large chromatic number. XII. Distant stars
Abstract
The Gyárfás-Sumner conjecture asserts that if 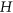 is a tree then every graph with bounded clique number and very large chromatic number contains
is a tree then every graph with bounded clique number and very large chromatic number contains 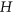 as an induced subgraph. This is still open, although it has been proved for a few simple families of trees, including trees of radius two, some special trees of radius three, and subdivided stars. These trees all have the property that their vertices of degree more than two are clustered quite closely together. In this paper, we prove the conjecture for two families of trees which do not have this restriction. As special cases, these families contain all double-ended brooms and two-legged caterpillars.
as an induced subgraph. This is still open, although it has been proved for a few simple families of trees, including trees of radius two, some special trees of radius three, and subdivided stars. These trees all have the property that their vertices of degree more than two are clustered quite closely together. In this paper, we prove the conjecture for two families of trees which do not have this restriction. As special cases, these families contain all double-ended brooms and two-legged caterpillars.



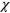 -bounded classes
-bounded classes
