ARTICLE

Counting degree sequences of spanning trees in bipartite graphs: A graph-theoretic proof

Corresponding Author

Anja Fischer

[email protected]

orcid.org/0000-0002-2812-043X

TU Dortmund University, Faculty of Business and Economics, Dortmund, Germany

Correspondence Anja Fischer, TU Dortmund University, Faculty of Business and Economics, Dortmund, Vogelpothsweg 87, D-44227, Germany. Email: [email protected]

Search for more papers by this author

Frank Fischer,

Frank Fischer

orcid.org/0000-0002-5154-6594

Johannes Gutenberg University Mainz, Institute of Computer Science, Mainz, Germany

Search for more papers by this author

Anja Fischer,

Corresponding Author

Anja Fischer

[email protected]

orcid.org/0000-0002-2812-043X

TU Dortmund University, Faculty of Business and Economics, Dortmund, Germany

Correspondence Anja Fischer, TU Dortmund University, Faculty of Business and Economics, Dortmund, Vogelpothsweg 87, D-44227, Germany. Email: [email protected]

Search for more papers by this author

Frank Fischer,

Frank Fischer

orcid.org/0000-0002-5154-6594

Johannes Gutenberg University Mainz, Institute of Computer Science, Mainz, Germany

Search for more papers by this author

First published: 16 January 2019

https://doi.org/10.1002/jgt.22449

Share a link

Email
Wechat
Bluesky

Abstract

Given a bipartite graph 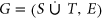$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0001$ with bipartition 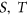$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0002$ each spanning tree in 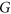$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0003$ has a degree sequence on 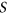$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0004$ and one on 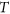$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0005$ . Löhne and Rudloff showed that the number of possible degree sequences on 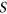$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0006$ equals the number of possible degree sequences on 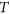$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0007$ . Their proof uses a non-trivial characterization of degree sequences by 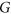$urn:x-wiley:03649024:media:jgt22449:jgt22449-math-0008$ -draconian sequences based on polyhedral results of Postnikov. In this paper, we give a purely graph-theoretic proof of their result.