Maximising 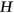-colourings of graphs

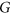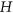For graphs and , an 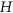-colouring of 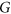is a map 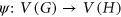such that 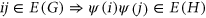. The number of -colourings of 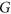is denoted by 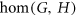. We prove the following: for all graphs 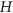and 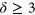, there is a constant such that, if 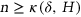, the graph 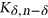maximises the number of 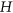-colourings among all connected graphs with 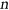vertices and minimum degree . This answers a question of Engbers. We also disprove a conjecture of Engbers on the graph 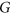that maximises the number of 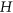-colourings when the assumption of the connectivity of 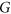is dropped. Finally, let 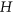be a graph with maximum degree 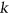. We show that, if 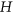does not contain the complete looped graph on 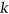vertices or 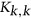as a component and 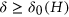, then the following holds: for 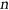sufficiently large, the graph 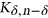maximises the number of 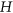-colourings among all graphs on 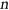vertices with minimum degree 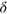. This partially answers another question of Engbers.