We investigate the independence number of two graphs constructed from a polarity of 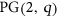$urn:x-wiley:03649024:media:jgt22442:jgt22442-math-0001$ . For the first graph under consideration, the Erdős-Rényi graph 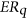$urn:x-wiley:03649024:media:jgt22442:jgt22442-math-0002$ , we provide an improvement on the known lower bounds on its independence number. In the second part of the paper, we consider the Erdős-Rényi hypergraph of triangles 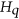$urn:x-wiley:03649024:media:jgt22442:jgt22442-math-0003$ . We determine the exact magnitude of the independence number of 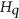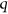$urn:x-wiley:03649024:media:jgt22442:jgt22442-math-0004$ , $urn:x-wiley:03649024:media:jgt22442:jgt22442-math-0005$ even. This solves a problem posed by Mubayi and Williford [On the independence number of the ErdŐs-RÉnyi and projective norm graphs and a related hypergraph, J. Graph Theory, 56 (2007), pp. 113-127, Open Problem 3].

REFERENCES

1V. Abatangelo, and B. Larato, A characterisation of Denniston’s maximal arcs, Geom. Dedicata 30 (1989), 197–203.
10.1007/BF00181551
Web of Science® Google Scholar
2W. G. Brown, On graphs that do not contain a Thomsen graph, Canad. Math. Bull. 9 (1966), 281–285.
10.4153/CMB-1966-036-2
Web of Science® Google Scholar
3R. H. F. Denniston, Some maximal arcs in finite projective planes, J. Combin. Theory 6 (1969), 317–319.
10.1016/S0021-9800(69)80095-5
Google Scholar
4P. Erdős, and A. Rényi, On a problem in the theory of graphs, Publ. Math. Inst. Hungar. Acad. Sci 7A (1962), 623–641.
Google Scholar
5Z. Füredi, Graphs without quadrilaterals, J. Combin. Theory Ser. B 34 (1983), 187–190.
10.1016/0095-8956(83)90018-7
Web of Science® Google Scholar
6Z. Füredi, On the number of edges of quadrilateral-free graphs, J. Combin. Theory Ser. B 68 (1996), 1–6.
10.1006/jctb.1996.0052
Web of Science® Google Scholar
7J. W. P. Hirschfeld, Projective geometries over finite fields, Oxford mathematical monographs, Oxford Science Publications, The Clarendon Press, Oxford University Press, New York, 1998.
Google Scholar
8S. A. Hobart, and J. Williford, The independence number for polarity graphs of even order planes, J. Algebraic Combin. 38 (2013), 57–64.
10.1007/s10801-012-0392-y
Web of Science® Google Scholar
9F. Lazebnik, and J. Verstraëte, On hypergraphs of girth five, Electron. J. Combin. 10 (2003), 1–15.
Web of Science® Google Scholar
10J. Loucks and C. Timmons, Triangle-free induced subgraphs of polarity graphs, available at https://arxiv.org/abs/1703.06347, 2017.
Google Scholar
11D. Mubayi, and J. Williford, On the independence number of the Erdős-Rényi and projective norm graphs and a related hypergraph, J. Graph Theory 56 (2007), 113–127.
10.1002/jgt.20251
Web of Science® Google Scholar
12T. D. Parsons, Graphs from projective planes, Aequ. Math. 14 (1976), no. 1-2, 167–189.
10.1007/BF01836217
Google Scholar

Citing Literature

Volume92, Issue2

October 2019

Pages 96-110

On the independence number of graphs related to a polarity

Abstract

REFERENCES

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the independence number of graphs related to a polarity

Abstract

REFERENCES

Citing Literature

References

Related

Information