Triangle-free graphs that do not contain an induced subdivision of K4 are 3-colorable
Maria Chudnovsky
Program for Applied and Computational Mathematics, Princeton University, Princeton, New Jersey
Search for more papers by this authorChun-Hung Liu
Program for Applied and Computational Mathematics, Princeton University, Princeton, New Jersey
Search for more papers by this authorCorresponding Author
Sophie Spirkl
Program for Applied and Computational Mathematics, Princeton University, Princeton, New Jersey
Correspondence Sophie Spirkl, Department of Mathematics, Rutgers University, Hill Center, Busch Campus, 110 Frelinghuysen Rd, Piscataway, NJ 08854. Email: [email protected]
Search for more papers by this authorNicolas Trotignon
Institut für Informatik, CNRS, LIP, ENS de Lyon, Université de Lyon, Lyon, France
Search for more papers by this authorKristina Vušković
School of Computing, University of Leeds, UK
Faculty of Computer Science, Union University, Belgrade, Serbia
Search for more papers by this authorMaria Chudnovsky
Program for Applied and Computational Mathematics, Princeton University, Princeton, New Jersey
Search for more papers by this authorChun-Hung Liu
Program for Applied and Computational Mathematics, Princeton University, Princeton, New Jersey
Search for more papers by this authorCorresponding Author
Sophie Spirkl
Program for Applied and Computational Mathematics, Princeton University, Princeton, New Jersey
Correspondence Sophie Spirkl, Department of Mathematics, Rutgers University, Hill Center, Busch Campus, 110 Frelinghuysen Rd, Piscataway, NJ 08854. Email: [email protected]
Search for more papers by this authorNicolas Trotignon
Institut für Informatik, CNRS, LIP, ENS de Lyon, Université de Lyon, Lyon, France
Search for more papers by this authorKristina Vušković
School of Computing, University of Leeds, UK
Faculty of Computer Science, Union University, Belgrade, Serbia
Search for more papers by this authorAbstract
We show that triangle-free graphs that do not contain an induced subgraph isomorphic to a subdivision of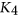 
are 3-colorable. This proves a conjecture of Trotignon and Vušković [J. Graph Theory. 84 (2017), no. 3, pp. 233–248].
REFERENCES
- 1M. Chudnovsky, A. Scott, and P. Seymour, Induced subgraphs of graphs with large chromatic number. II. Three steps towards Gyárfás’ conjectures, J. Combin. Theory Ser. B 118 (2016), 109–128.
- 2M. Chudnovsky et al., Excluding induced subdivisions of the bull and related graphs, J. Graph Theory 71 (2012), 49–68.
- 3R. J. Duffin, Topology of series-parallel networks, J. Math. Anal. Appl. 10 (1965), no. 2, 303–318.
- 4A. Gyárfás, Problems from the world surrounding perfect graphs, Zastosowania Mat. Appl. Math. 19 (1987), 413–441.
- 5T. Karthick and F. Maffray, Square-free graphs with no six-vertex induced path, arXiv preprint, arXiv:1805.05007.
- 6T. Karthick, and F. Maffray, Vizing bound for the chromatic number on some graph classes, Graphs Combin. 32 (2016), 1447–1460.
- 7T. Karthick, and S. Mishra, On the chromatic number of (
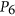, diamond)-free graphs, Graphs Combin. 34 (2018), 677–692.
- 8T. Kloks, H. Müller, and K. Vušković, Even-hole-free graphs that do not contain diamonds: A structure theorem and its consequences, J. Combin. Theory Ser. B 99 (2009), 733–800.
- 9M. Radovanović, and K. Vušković, A class of 3-colorable triangle-free graphs, J. Graph Theory 72 (2013), no. 4, 430–439.
- 10N. K. Le, Chromatic number of
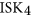-free graphs, Graphs Combin. 33 (2017), no. 6, 1635–1646.
- 11N. K. Le, Detecting an induced subdivition of
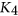, Electron. Notes Discrete Math. 62 (2017), 315–320.
10.1016/j.endm.2017.10.054 Google Scholar - 12B. Lévêque, F. Maffray, and N. Trotignon, On graphs with no induced subdivision of
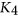, J. Combin. Theory Ser. B 102 (2012), no. 4, 924–947.
- 13K. Menger, Zur allgemeinen Kurventheorie, Fund. Math. 10.1 (1927), 96–115.
10.4064/fm-10-1-96-115 Google Scholar
- 14A. Pawlik et al., Triangle-free intersection graphs of line segments with large chromatic number, J. Combin. Theory Ser. B 105 (2014), 6–10.
- 15A. Scott, Induced trees in graphs of large chromatic number, J. Graph Theory 24 (1997), 297–311.
- 16N. Trotignon, and K. Vušsković, A structure theorem for graphs with no cycle with a unique chord and its consequences, J. Graph Theory 63 (2010), no. 1, 31–67.
- 17N. Trotignon, and K. Vušković, On triangle-free graphs that do not contain a subdivision of the complete graph on four vertices as an induced subgraph, J. Graph Theory 84 (2017), no. 3, 233–248.
