Hereditary graph classes: When the complexities of coloring and clique cover coincide
Alexandre Blanché
Département Informatique et Télécommunications, École normale supérieure de Rennes, Campus de Ker Lann, Bruz, France
Search for more papers by this authorKonrad K. Dabrowski
Department of Computer Science, Durham University, Durham, United Kingdom
Search for more papers by this authorMatthew Johnson
Department of Computer Science, Durham University, Durham, United Kingdom
Search for more papers by this authorCorresponding Author
Daniël Paulusma
Department of Computer Science, Durham University, Durham, United Kingdom
Correspondence Daniël Paulusma, Department of Computer Science, Durham University, South Road, Durham DH1 3LE, United Kingdom. Email: [email protected]
Search for more papers by this authorAlexandre Blanché
Département Informatique et Télécommunications, École normale supérieure de Rennes, Campus de Ker Lann, Bruz, France
Search for more papers by this authorKonrad K. Dabrowski
Department of Computer Science, Durham University, Durham, United Kingdom
Search for more papers by this authorMatthew Johnson
Department of Computer Science, Durham University, Durham, United Kingdom
Search for more papers by this authorCorresponding Author
Daniël Paulusma
Department of Computer Science, Durham University, Durham, United Kingdom
Correspondence Daniël Paulusma, Department of Computer Science, Durham University, South Road, Durham DH1 3LE, United Kingdom. Email: [email protected]
Search for more papers by this authorAbstract
A graph is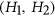 
-free for a pair of graphs 
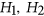if it contains no induced subgraph isomorphic to 
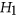or 
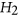. In 2001, Král et al initiated a study into the complexity of coloring for 
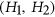-free graphs. Since then, others have tried to complete their study, but many cases remain open. We focus on those 
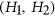-free graphs where 
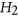is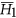 
, the complement of 
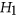. As these classes are closed under complementation, the computational complexities of coloring and clique cover coincide. By combining new and known results, we are able to classify the complexity of coloring and clique cover for 
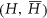-free graphs for all cases except when 
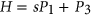for 
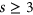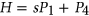or 
for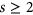 
. We also classify the complexity of coloring on graph classes characterized by forbidding a finite number of self-complementary induced subgraphs, and we initiate a study of 
-
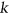coloring for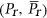 
-free graphs.
REFERENCES
- 1A. Blanché, K. K. Dabrowski, M. Johnson, V. V. Lozin, D. Paulusma, and V. Zamaraev, Clique-width for graph classes closed under complementation, Proceedings 42nd International Symposium on Mathematical Foundations of Computer Science (Leibniz International Proceedings in Informatics vol 83), (2017), pp. 73:1–73:14.
- 2F. Bonomo, M. Chudnovsky, P. Maceli, O. Schaudt, M. Stein, and M. Zhong, Three-coloring and list three-coloring of graphs without induced paths on seven vertices, Combinatorica. 38 (2018), 779-801.
- 3A. Brandstädt, H.-O. Le, and R. Mosca, Gem- and co-gem-free graphs have bounded clique-width, Int. J. Found. Comput. Sci. 15 (2004), 163–185.
- 4A. Brandstädt, H.-O. Le, and R. Mosca, Chordal co-gem-free and (
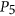, gem)-free graphs have bounded clique-width, Discrete Appl. Math. 145 (2005), 232–241.
- 5H. Broersma, P. A. Golovach, D. Paulusma, and J. Song, Determining the chromatic number of triangle-free
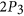-free graphs in polynomial time, Theor. Comput. Sci. 423 (2012), 1–10.
- 6K. Cameron and C. T. Hoàng, Solving the clique cover problem on (bull, C4)-free graphs, 2017, CoRR, arXiv: 1704.00316.
- 7M. Chudnovsky, J. Goedgebeur, O. Schaudt, and M. Zhong, Obstructions for three-coloring graphs with one forbidden induced subgraph, Proc. Annu. ACM-SIAM Symp. Discrete Algorithms, 2016, pp. 1774–1783.
- 8M. Chudnovsky, S. Huang, S. Spirkl, and M. Zhong, List-three-coloring graphs with no induced P6+rP3, 2018, CoRR, arXiv: 1806.11196.
- 9M. Chudnovsky, N. Robertson, P. D. Seymour, and R. Thomas, The strong perfect graph theorem, Ann. Math. 164 (2006), 51–229.
- 10M. Chudnovsky, S. Spirkl, and M. Zhong, Four-coloring-P6-free graphs. I. Extending an excellent precoloring, 2018, arXiv: 1802.02282.
- 11M. Chudnovsky, S. Spirkl, and M. Zhong, Four-coloring-P6-free graphs. II. Finding an excellent precoloring, 2018, CoRR, arXiv: 1802.02283.
- 12J.-F. Couturier, P. A. Golovach, D. Kratsch, and D. Paulusma, List coloring in the absence of a linear forest, Algorithmica 71 (2015), 21–35.
- 13K. K. Dabrowski, F. Dross, and D. Paulusma, Colouring diamond-free graphs, J. Comput. Syst. Sci. 89 (2017), 410–431.
- 14K. K. Dabrowski, P. A. Golovach, and D. Paulusma, Colouring of graphs with Ramsey-type forbidden subgraphs, Theor. Comput. Sci. 522 (2014), 34–43.
- 15K. K. Dabrowski and D. Paulusma, Classifying the clique-width of
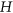-free bipartite graphs, Discrete Appl. Math. 200 (2016), 43–51.
- 16T. Emden-Weinert, S. Hougardy, and B. Kreuter, Uniquely colourable graphs and the hardness of colouring graphs of large girth, Comb. Probab. Comput. 7 (1998), 375–386.
- 17M. R. Garey and D. S. Johnson, Computers and intractability: A guide to the theory of NP-completeness, W. H. Freeman & Co., New York, NY, 1979.
- 18P. A. Golovach, M. Johnson, D. Paulusma, and J. Song, A survey on the computational complexity of colouring graphs with forbidden subgraphs, J. Graph Theory 84 (2017), 331–363.
- 19M. Grötschel, L. Lovász, and A. Schrijver, Polynomial algorithms for perfect graphs, Ann. Discrete Math. 21 (1984), 325–356.
- 20P. Hell and S. Huang, Complexity of coloring graphs without paths and cycles, Discrete Appl. Math. 216 (2017), 211–232.
- 21C. T. Hoàng, M. Kaminski, V. V. Lozin, J. Sawada, and X. Shu, Deciding
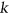-colorability of 
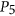-free graphs in polynomial time, Algorithmica 57 (2010), 74–81.
- 22C. T. Hoàng and D. A. Lazzarato, Polynomial-time algorithms for minimum weighted colorings of
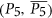-free graphs and similar graph classes, Discrete Appl. Math. 186 (2015), 106–111.
- 23S. Huang, Improved complexity results on
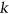-coloring 
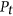-free graphs, Eur. J. Comb. 51 (2016), 336–346.
- 24M. Kamiński, V. V. Lozin, and M. Milanič, Recent developments on graphs of bounded clique-width, Discrete Appl. Math. 157 (2009), 2747–2761.
- 25S. Kitaev and V. V. Lozin, Words and graphs (Monographs in Theoretical Computer Science An EATCS Series), Springer, New York, NY, 2015.
- 26D. Kobler and U. Rotics, Edge dominating set and colorings on graphs with fixed clique-width, Discrete Appl. Math. 126 (2003), 197–221.
- 27D. Kráľ, J. KratochvÍl, Zs. Tuza, and G. J. Woeginger, Complexity of coloring graphs without forbidden induced subgraphs, Proc. 27th Int. Workshop Graph-Theoretic Concepts Comput. Sci. (Lecture Notes in Computer Science, vol 2204), 2001, pp. 254–262
- 28L. Lovász, Coverings and coloring of hypergraphs, Congressus Numerantium 8 (1973), 3–12.
- 29V. V. Lozin, Bipartite graphs without a skew star, Discrete Math. 257 (2002), 83–100.
- 30V. V. Lozin, and M. Kamiński, Coloring edges and vertices of graphs without short or long cycles, Contrib. Discrete Math. 2 (2007).
- 31V. V. Lozin and D. S. Malyshev, Vertex coloring of graphs with few obstructions, Discrete Appl. Math. 216 (2017), 273–280.
- 32V. V. Lozin and D. Rautenbach, On the band-, tree-, and clique-width of graphs with bounded vertex degree, SIAM J. Discrete Math. 18 (2004), 195–206.
- 33J. A. Makowsky and U. Rotics, On the clique-width of graphs with few
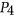’s, Int. J. Found. Comput. Sci. 10 (1999), 329–348.
10.1142/S0129054199000241 Google Scholar - 34D. S. Malyshev, The coloring problem for classes with two small obstructions, Optim. Lett. 8 (2014), 2261–2270.
- 35D. S. Malyshev, Two cases of polynomial-time solvability for the coloring problem, J. Comb. Optim. 31 (2016), 833–845.
- 36D. S. Malyshev and O. O. Lobanova, Two complexity results for the vertex coloring problem, Discrete Appl. Math. 219 (2017), 158–166.
- 37S. Oum and P. D. Seymour, Approximating clique-width and branch-width, J. Comb. Theory B 96 (2006), 514–528.
- 38F. P. Ramsey, On a problem of formal logic, Proc. Lond. Math. Soc. s2-30 (1930), 264–286.
10.1112/plms/s2-30.1.264 Google Scholar
- 39D. Schindl, Some new hereditary classes where graph coloring remains NP-hard, Discrete Math. 295 (2005), 197–202.
- 40R. E. Tarjan, Decomposition by clique separators, Discrete Math. 55 (1985), 221–232.
