Extrapolation Results on General Besov-Hölder-Lipschitz Spaces

General Besov -Hölder-Lipschitz spaces 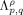(ℝⁿ ), where ρ is an arbitrary q-admissible function, are introduced and extrapolation characterizations concerning these spaces are given. We present some concrete examples and, in particular, we very easily obtain the extrapolation results [16, Proposition 2.5], [8, Proposition 4.2] and [14, Proposition 7]. New extrapolation results, as far as we are aware, concerning the spaces 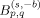(ℝⁿ ), with s > 0, b ≥ 0, 1 ≤ p ≤ +∞ and 0 < q ≤ +∞ are also given. We apply these extrapolation methods to give a different proof of some embeddings of certain Besov or Leopold spaces in spaces of Lipschitz type proved by Haroske, cf. [14, Proposition 11, Corollary 23 (i)]. We also improve [14, Proposition 11] when q = min(p, 2) and 1 ≤p < +∞, cf. Proposition 5.6.