Abstract and Applied Analysis
Volume 2013, Issue 1 532041
Research Article
Open Access

Scaled Diagonal Gradient-Type Method with Extra Update for Large-Scale Unconstrained Optimization

Mahboubeh Farid, 

Corresponding Author

Mahboubeh Farid

Department of Mathematics, University Putra Malaysia, 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author
Wah June Leong, 

Wah June Leong

Department of Mathematics, University Putra Malaysia, 43400 Serdang, Selangor, Malaysia upm.edu.my

Search for more papers by this author
Najmeh Malekmohammadi, 

Najmeh Malekmohammadi

Department of Mathematics, Islamic Azad University, South Tehran Branch, Tehran 1418765663, Iran azad.ac.ir

Search for more papers by this author
Mustafa Mamat, 

Mustafa Mamat

Department of Mathematics, Faculty of Science and Technology, University Malaysia Terengganu, 21030 Kuala Terengganu, Malaysia umt.edu.my

Search for more papers by this author
First published: 27 March 2013
https://doi.org/10.1155/2013/532041
Citations: 2
Academic Editor: Guanglu Zhou

Abstract

We present a new gradient method that uses scaling and extra updating within the diagonal updating for solving unconstrained optimization problem. The new method is in the frame of Barzilai and Borwein (BB) method, except that the Hessian matrix is approximated by a diagonal matrix rather than the multiple of identity matrix in the BB method. The main idea is to design a new diagonal updating scheme that incorporates scaling to instantly reduce the large eigenvalues of diagonal approximation and otherwise employs extra updates to increase small eigenvalues. These approaches give us a rapid control in the eigenvalues of the updating matrix and thus improve stepwise convergence. We show that our method is globally convergent. The effectiveness of the method is evaluated by means of numerical comparison with the BB method and its variant.

1. Introduction

In this paper, we consider the unconstrained optimization problem
()
where f(x) is a continuously differentiable function from Rn to R. Given a starting point x0, using notations gk = g(xk) = ∇f(xk) and Bk as an approximation to the Hessian Gk = [∇2f(xk)], the quasi-Newton-based methods for solving (1) are defined by the iteration
()
where the stepsize αk is determined through an appropriate selection. The updating matrix Bk is usually required to satisfy the quasi-Newton equation
()
where sk−1 = xk − xk−1 and yk−1 = gk − gk−1. One of the widely used quasi-Newton method to solve general nonlinear minimization is the BFGS method, which uses the following updating formula:
()
On the numerical aspect, this method supersedes most of the optimization methods; however, it needs O(n2) storage which makes it unsuitable for large-scale problems.
On the other hand, an ingenious stepsizes selection for gradient method was proposed by Barzilai and Borwein [1] in which the updating scheme is defined by
()
where Dk = (1/αk)I and .

Since that, the study of new effective methods in the frame of BB-like gradient methods becomes an interesting research topic for a wide range of mathematical programming; for example, see [2–10]. However, it is well known that BB method cannot guarantee a descent in the objective function at each iteration and the extent of the nonmonotonicity depends in some way on the size of the condition number of objective function [11]. Therefore, the performance of BB method is greatly influenced by the condition of the problem (particularly, condition number of the Hessian matrix). Some new fixed stepsizes gradient-type methods of BB kind are proposed by [12–16] to overcome these difficulties. In contrast with the BB approach in which the stepsize is computed by means of a simple approximation of the Hessian in the form of scalar multiple of identity, these proposed methods consider approximation of the Hessian and its inverse in diagonal matrix form based on the weak secant equation and quasi-cauchy relation, respectively (for more details see [15, 16]). Though these diagonal updating methods are efficient, their performance can be greatly affected by solving ill-conditioned problems. Thus, there is room for improve on the quality of the diagonal updates formulation. Since methods as described in [15, 16] have useful theoretical and numerical properties, it is desirable to derive a new and more efficient updating frame for general functions. Therefore our aim is to improve the quality of diagonal updating when it is poor in approximating Hessian.

This paper is organized as follows. In the next section, we describe our motivation and propose our new-gradient type method. The global convergence of the method under mild assumption will be established in Section 3. Numerical evidence of the vast improvements due to the new approach is given in Section 4. Finally, conclusion is made in the last section.

2. Scaling and Extra Updating

Assume that Bk is positive definite, and let {yk} and {sk} be two sequences of n-vectors such that for all k. Because it is usually difficult to satisfy the quasi-Newton equation (3) with a nonsingular Bk+1 of the diagonal form, one can consider satisfying it in some directions. If we project the quasi-Newton equation (3) (also called the secant equation), in a direction υ such that , then it gives
()
If υ = sk is chosen, it leads to the so-called weak-secant relation,
()
Under this weak-secant equation, [15, 16] employ variational technique to derive updating matrix that approximates the Hessian matrix diagonally. The resulting update is derived to be the solution of the following variational problem:
()
and gives the corresponding solution Bk+1 as follows:
()
where , sk,i is the ith component of the vector sk, and tr  denotes the trace operator.

Note that when , the resulting Bk+1 is not necessarily positive definite and it is not appropriate for use within a quasi-Newton-based algorithm. Thus, it is desirable to propose a technique to measure the quality of Bk in terms of its Rayleigh quotient and try to find a way to improve “poor” quality Bk before calculating Bk+1. For this purpose, it will be useful to propose, at first quality a criterion to distinguish between poor, and acceptable quality of Bk.

Let us begin by considering the curvature of an objective function, f in direction sk, which is represented by
()
where is the average Hessian matrix along sk. Since it is not practical to compute the eigenvalue of the Hessian matrix in each iteration, we can estimate its relative size on the basis of the scalar
()
If ρk > 1, it implies that the eigenvalues of Bk approximated by its Rayleigh are relatively small compared to those of the local Hessian matrix at xk. In this condition, we find that the strategy of extra update [17] seems to be useful for improving the quality of Bk by rapidly increasing its eigenvalues up to those of the actual Hessian relatively. This is done by updating Bk twice to obtain :
()
()
and use it to obtain, finally, the updated Bk+1:
()
On the other hand, when ρk < 1, it implies that the eigenvalue of Bk represented by its Rayleigh is relatively large and we have . In this case, we should suggest a useful strategy to encounter this drawback. As we reviewed before, the updating scheme may generate nonpositive definite Bk+1 when Bk has large eigenvalues relative to those possible values of , that is, when . On the contrary, this argument disappears when the eigenvalues of Bk are small (i.e., ). This suggests that the scaling should be made to scale down Bk, that is, choosing ρk < 1 only when and take ρk = 1, whenever . Combining these two arguments, we choose the scaling parameter ρk such that
()
This scaling resembles the Al-Baali [18] scaling that is applied within the Broyden family. Because the value of γk is always <1, then by incorporating the scaling to Bk, it decreases the large eigenvalues of Bk constantly, and consequently we can keep positive definiteness of Bk+1 (since ), which is an important property in descent method. In this case, the following updating:
()
will be used. To this end, we have the following general updating scheme for Bk+1:
()
where and γk are given by (13) and (15), respectively.

An advantage of using (17) is that the positive definiteness of Bk+1 can be guaranteed in all iterations. This property is not exhibited in the other diagonal updating formula such as those in [15, 16]. Note that there is no extra storage required to impose our strategy and the cost of computing is also not increased significantly throughout the entire iteration. Now we can state the steps of our new diagonal-gradient method algorithm with the safeguarding strategy for monotonicity as follows.

2.1. ESDG Algorithm

Step 1. Choose an initial point x0 ∈ Rn and a positive definite matrix B0 = I. Let θ ∈ (1,2). Set k : = 0.

Step 2. Compute gk. If ∥gk∥ ≤ ϵ, stop.

Step 3. If k = 0, set x1 = x0 − g0/∥g0∥.

Step 4. Compute , and calculate αk > 0 such that the following condition holds: where and σ ∈ (0,1) is a given constant.

Step 5. If k ≥ 1, let and compute ρk and γk by (11) and (15), respectively. If ρk < θ then update Bk+1 by (16).

Step 6. If ρk ≥ θ then compute and by (12), (13), respectively, and then update as defined Bk+1 (14).

Step 7. Set k : = k + 1, and return to Step 2.

In Step 4, we employ the nonmonotone line search of [19, 20] to ensure the convergence of the algorithm. However, some other line search strategies may also be used.

3. Convergence Analysis

This section is devoted to study the convergence behavior of ESDG method. We will establish the convergence of the ESDG algorithm when applied to the minimization of a strictly convex function. To begin, we give the convergence result, which is due to Grippo et al. [21] for the step generated by the nonmonotone line search algorithm. Here and elsewhere, ∥·∥ denotes the Euclidean norm.

Theorem 1. Assume that f is a strictly convex function and its gradient g satisfies the Lipschitz condition. Suppose that the nonmonotone line search algorithm is employed in a case that the steplength, αk, satisfies

()
where , with m ≤ k and σ ∈ (0,1), and the search direction dk is chosen to obey the following conditions. There exist positive constants c1 and c2 such that
()
for all sufficiently large k. Then the iterates xk generated by the nonmonotone line search algorithm have the property that
()

To prove that the ESDG algorithm is globally convergent, it is sufficient to show that the sequence {∥Bk∥} generated by (17) is bounded both above and below, for all finite k so that its associated search direction satisfies condition (19). Since Bk is diagonal, it is enough to show that each element of Bk, say , i = 1, …, n, is bounded above and below by some positive constants. The following theorem gives the boundedness of {∥Bk∥}.

Theorem 2. Assume that f is strictly convex function where there exist positive constants m and M such that

()
for all x, z ∈ Rn. Let {∥Bk∥} be a sequence generated by the ESDG method. Then ∥Bk∥ is bounded above and below for all finite k, by some positive constants.

Proof. Let be the ith element of Bk. Suppose that B0 is chosen such that where ω1, ω2 are some positive constants. It follows from (17) and the definition of γ in (15) that we have

()
where
()
Moreover, by (21) and (11), we obtain
()
Case  1. When ρ0 ≤ 1: by (24), one can obtain
()
Thus, it implies that .

Case  2. When ρ0 > 1: from (3), we have

()
Because ρ0 > 1 also implies that , using this fact and (24) give
()
Let s0,M be the largest component in magnitude of s0, that is, . Then it follows that , and (27) becomes
()
Using (28) and the same argument as previously mentioned, we can also show that
()
Hence in both cases, is bounded above and below, by some positive constants. Since the upper and lower bounds for are independent of k, respectively, we can proceed by using induction to show that is bounded, for all finite k.

4. Numerical Results

In this section we present the results of numerical investigation for ESDG method on different test problems. We also compare the performance of our new method with that of the BB method and that of MDGRAD method which is implemented using SMDQN of [22] with a same nonmonotone strategy as the ESDG method. Our experiments are performed on a set of 20 nonlinear unconstrained problems with dimensions ranging from 10 to 104 (Table 1).

Table 1. Test problem and its dimension.
Problem References
Extended Freudenstein and Roth, Extended Trigonometric,  
Broyden Tridiagonal, Extended Beale, Generalized Rosenbrock, Moré et al. [24]
Extended Tridiagonal 2, Extended Himmelblau, Raydan 2, EG2,  
Extended Three Exponential Terms, Raydan 1, Generalized PSC1,  
Quadratic QF2, Generalized Tridiagonal 1, Perturbed Quadratic,  
Diagonal 2, Diagonal 3, Diagonal 5, Almost perturbed Quadratic,  
Hager, diagonal 4 Andrei [23]

These test problems are taken from [23, 24]. The codes are developed with Matlab 7.0. All runs are performed on a PC with Core Duo CPU. For each test, the termination condition is ∥g(xk)∥ ≤ 10−4. The maximum number of iterations is set to 1000.

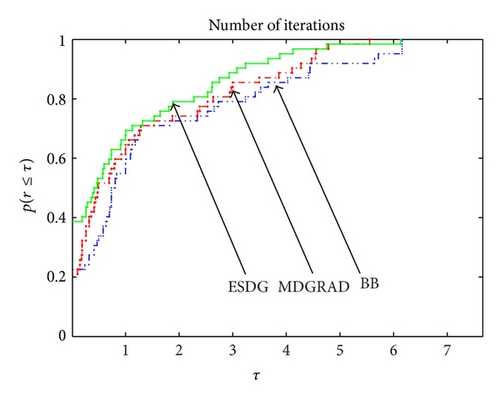
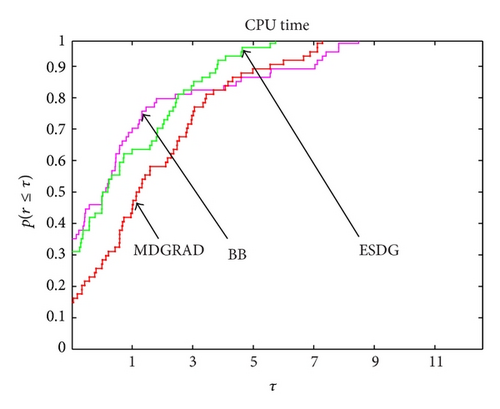
Figures 1 and 2 show the efficiency of ESDG method when compared to MDGRAD and BB methods. Note that ESDG method increases the efficiency of Hessian approximation devoid of increasing the number of storages. Figure 2 also shows the implementation of the ESDG method with BB and MDGRAD methods using the CPU time as a measure. This figure shows that ESDG method is again faster than MDGRAD method in most problems and requires reasonable time to solve large-scale problems when compares to the BB method. Finally, we can conclude that our experimental comparisons indicate that our extension is very beneficial to the performance.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Performance profile based on iterations.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Performance profile based on CPU time per iteration.

5. Conclusion

We have presented a new diagonal gradient method for unconstrained optimization. Numerical study of the proposed method when compared with BB and MDGRAD methods is also performed. Based on our numerical experiments, we can conclude that ESDG method is significantly preferable compared to the BB and MDGRAD methods. Particularly, the ESDG method is proven to be a good option for large-scale problems when high-memory locations are required. In view of the remarkable performance of ESDG method, globally converged and with only O(n) storage, we can expect that our proposed method would be useful for unconstrained large-scale optimization problems.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.