Volume 2013, Issue 1 496243

Research Article

Open Access

Hydrodynamic Trapping of Particles in an Expansion-Contraction Microfluidic Device

Ruijin Wang,

Corresponding Author

Ruijin Wang

[email protected]

orcid.org/0000-0001-8126-4339

Zhejiang University of Science and Technology, Hangzhou 310023, China zust.edu.cn

Centre of Smart Interface, Technische Universität Darmstadt, 24878 Darmstadt, Germany tu-darmstadt.de

Search for more papers by this author

Ruijin Wang,

Corresponding Author

Ruijin Wang

[email protected]

orcid.org/0000-0001-8126-4339

Zhejiang University of Science and Technology, Hangzhou 310023, China zust.edu.cn

Centre of Smart Interface, Technische Universität Darmstadt, 24878 Darmstadt, Germany tu-darmstadt.de

Search for more papers by this author

First published: 27 November 2013

https://doi.org/10.1155/2013/496243

Citations: 6

Academic Editor: Jianzhong Lin

Share a link

Email
Wechat
Bluesky

Abstract

Manipulation and sorting of particles utilizing microfluidic phenomena have been a hot spot in recent years. Here, we present numerical investigations on particle trapping techniques by using intrinsic hydrodynamic effects in an expansion-contraction microfluidic device. One emphasis is on the underlying fluid dynamical mechanisms causing cross-streamlines migration of the particles in shear and vortical flows. The results show us that the expansion-contraction geometric structure is beneficial to particle trapping according to its size. Particle Reynolds number and aspect ratio of the channel will influence the trapping efficiency greatly because the force balance between inertial lift and vortex drag forces is the intrinsic reason. Especially, obvious inline particles contribution presented when the particle Reynolds number being unit. In addition, we selected three particle sizes (2, 7, and 15 μm) to examine the trapping efficiency.

1. Introduction

Microfluidics has greatly interested many researchers in recent years, and has been widely used in the areas of nanomaterials preparation, pharmaceutical analysis, protein engineering, and so on [1–4]. Manipulation and sorting particles suspended in microflow are often applied to biomedical area. Separating targeted particles from the detect solution is an important process. Not a few techniques such as membrane filtration, fluorescence, or magnetic particle sorting were developed in recent years, and they have a wide range of applications [5–7]. However, microfluidic-based devices introduce several advantages, such as higher efficiency, lower sample buffer consumption, fine spatial resolution, and lower cost [8]. In addition, microfluidic-based device can trap particles based on their intrinsic physical characteristics. Hydrodynamic manipulation of particles in an expansion-contraction microfluidic device is a passive method by harnessing microchannel geometrical effects and nonlinear hydrodynamic forces and needs not any application of external force leading to a complicated device structure.

Passive methods used to trapping particles by exerting hydrodynamic force are arising in microfluidic devices. The main approaches are the cross-stream migration of suspended particles in confined flows and microvortical flow. The microvortex generated in sudden expansion is of great importance for particle manipulation. Researchers have gained some beneficial research results [9–11] in the theoretical analysis and experimental investigations on the formation of vortices in different microchannel configurations. Jiang et al. [9] numerically investigated the flow field under various inlet flow rates and cavity structures and then systematically studied the flow features of the vortex and Dean flow in this channel by LBM. Bălan et al. [10] investigated the dynamics of the vortices generated in the vicinity of Y- and T-microbifurcations with one occluded branch. The velocity distribution and streamlines were obtained through the experiments and numerical simulations. Karimi et al. [11] concentrated their study on the dynamical mechanisms of cross stream migration particles in shear and vortical flows. Tsai et al. [12–14] found that Reynolds number and aspect ratio are both influential factors for flow patterns in a suddenly expansion microchannel. Park et al. [15] developed a kind of microfluidic method for focusing on microparticles through the combined use of inertial lift forces and turbulent secondary flows in a patterned microchannel. Furthermore, some particles trapping applications of the microvortices in an expansion-contraction microchannel have been presented in recent years [16, 17]. According to their research work, in the contraction part, particles flow under the balance of shear-gradient lift force and wall effect lift force. When the particles move into the expansion part, wall effect lift force disappears and the shear-gradient lift force leads particles to the vortex formed in the orifice. Lee’s group [18, 19] demonstrated a blood plasma separation scheme by employing the unilateral contraction-expansion array microchannel with a low aspect ratio. Small particles are driven predominantly by Dean drag force while the larger ones are lifted by the inertial force and stay close to their previous positions, leading to the isolation of different size particles. The inlet flow rate should be appropriately controlled to avoid particles migration into the vortex in the orificial under a high flow rate.

In the present research, microvortex in the expansion-contraction microchannel is numerically studied in order to understand the particle migration mechanism. The particles distribution and equilibrium position will vary with the change of inlet flow rate and geometry dimensions. Moreover, the research object is also to gain an insight into what condition being beneficial to the particle trapping efficiency for varying particle sizes and to supply the design foundations of such a microfluidic device.

2. Problem Description

2.1. Geometric Model and Parameter Settings

The microdevice under investigation is presented in Figure 1. There are 3 orifices in order to separate the varying particle size distinctly. The distance from inlet to the first orifice is 2000 μm, and the width of channel and orifice is 200 and 800 μm (with another being 400), respectively. The spacing distance between 2 orifices is 500 μm. The depth of the entire device is set to be 200 μm. The dimension of the orifice is 800 × 800 μm. Inlet is injected with deionized water with polystyrene microspheres being at the size of 2, 7, and 15 μm (corresponding to the size of platelet, red blood cell and white blood cell). The outlet for drainage is long enough off the last orifice, so we are able to obtain distinct separation in terms of particle size. Full-developed velocity profile is set at inlet, while the outflow is set at the outlet. The reference atmospheric pressure is given at the inlet, and the no-slip condition is used at the walls.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Geometric model of the expansion-contraction microfluidic device.

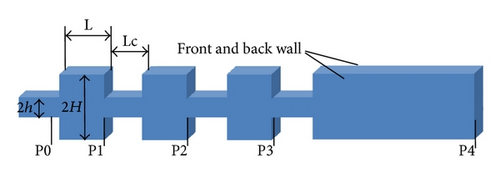
The settings of carried fluid properties: the viscosity, density, specific heat, and thermal conductivity of continuous phase are 1.003 g/m·s, 0.9982 g/cm³, 4180 J/kg·K, and 0.6 W/m·K, respectively. Density and specific heat of polystyrene microspheres are 1.055 g/cm³ and 1300 J/kg·K.

2.2. Numerical Model

The numerical model includes the continuity equation, Navier-Stokes equation which is still valid in current microchannel flow, and continuity equation for volume fraction

()

where p is the pressure, μ is the dynamic viscosity, and ρ is the density,

The particle continuity is derived from Buongiorno [20]. In our simulation, it is considered to be a dilute mixture (about 0.5% wt). Brownian diffusion can be regarded as the only slip mechanism for particle transport at low Reynolds number in microflow. They are incorporated into the particle transport equation as follows:

()

where α_p denotes the particle volume fraction. Brownian diffusion is described by the terms on the right hand side. D_B is Brownian diffusion coefficient. The coefficients read as

()

where k_B denotes Boltzmann’s constant, μ_b the viscosity of carried fluid, and d_p the particle diameter. The bulk fluid (carried fluid) is set to be zero.

There is still a lack of accurate theoretical models for the prediction of the viscosity the fluid containing particles. Normally, empirical laws [21] to predict the viscosity are

()

2.3. Method Validation

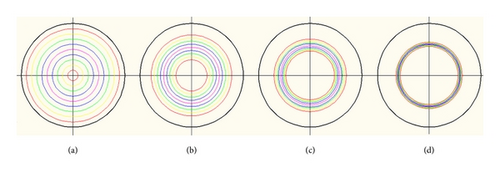
In order to verify the availability of the numerical model, we simulated numerically the flow with particles in a circular capillary. The particles distributions are shown in Figure 2. The equilibrium position is about 0.6 radius, being in good agreement with the theoretical results. We confirm the availability of our numerical model for the particle-laden microflow.

3. Results and Discussion

3.1. Particle Trapping Mechanism

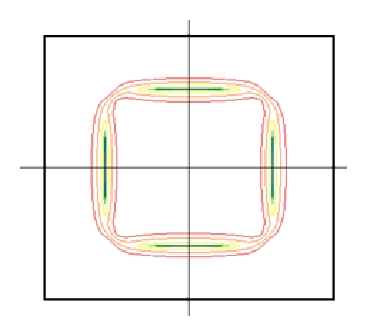
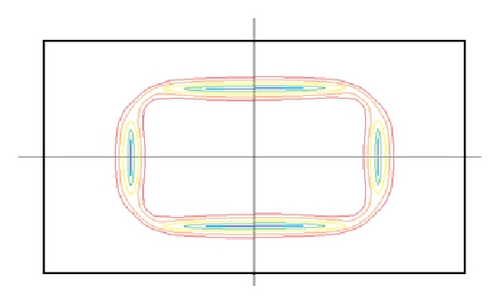
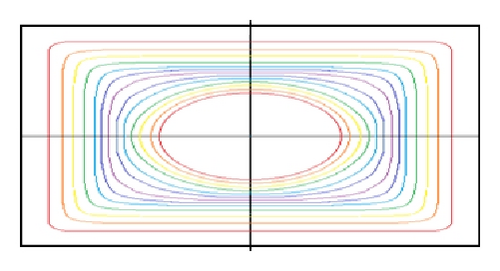
When particles are suspended in the carried fluid, the particle behavior is affected by the inertial and viscous forces occurring in the interaction with fluid. According to a number of theoretical analyses, the inertial migration phenomenon can be explained by a shear-gradient-induced lift force that causes particles to migrate away from the axis of pipe and a wall-effect-induced lift force that repels particles away from a pipe wall [22, 23]. This was proved to be right by our simulation results in Figure 2. In the case of square ducts, particles were concentrated near four walls (top, bottom, left, and right) [24]. We also simulated manifold geometries with varying aspect ratio (AR), and the results were shown in Figure 3. Numerical results show us that the particles distribution in almost in two lines when the aspect ratio is larger than 3 (see Figures 3(c) and 3(d)). This is the basis of hydrodynamic manipulation of particles in an expansion-contraction microfluidic device.

The channel geometry of multiorifices pattern (expansion-contraction structure) was designed so as to transform the particle distribution in a cross section of a straight channel and subsequently concentrate particles close to both side walls of channel. The mechanism of particle enrichment is based on the vortex flow due to the suddenly expansion channel, as shown in Figure 4. In this case, the wall-effect-induced lift forces are weakened compared to the shear-gradient-induced lift force; the reason is probably the long distance from the main stream to the side walls. The majority of particles can be focused near sidewalls as long as they pass through a series of contraction/expansion channels. The mechanism of particle migration induced by solely inertial lift forces cannot explain the dissimilarity for various particle sizes, because the size-based particle separation in a multiorifices microchannel is driven by a combination of two fluid-mechanical forces: inertial lift force and the momentum change over certain time interval is equivalent to inertial force. Inertial forces consist of two parts: inertial lift force and momentum-change-induced inertial force. The inertial lift force is caused by the lateral pressure gradient exerted on a particle, and the momentum-change-induced inertial force can be calculated by an equation. According to the momentum change over a certain time interval which is equivalent to inertial force, the particle migration velocity under consideration of the lateral migration driven by the inertial force can be obtained [25] by

()

Therefore, important dimensionless parameter named particle Reynolds number should be defined, because we are able to estimate the fluid dynamic phenomenon of particle flowing through a microchannel by using it. It is defined as the ratio of the inertial lift force and momentum-change-induced inertial force as

()

Here, d is the particle diameter, D_h is the hydraulic diameter of the channel, U_m is the maximum flow velocity in the channel, and ν is the kinematic viscosity of the carried liquid, μ is the dynamic viscosity. For Re_p bigger than 1, the inertial force becomes a dominant parameter for driving the lateral migration of particles transverse to fluid streamlines. In contrast, in the case of Re_p less than 1, the particle behavior is strongly promoted to follow the flow pattern by a viscous drag force acting on the particle surface.

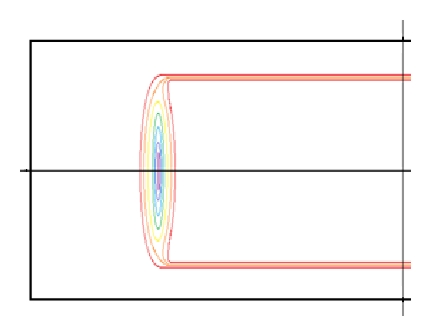
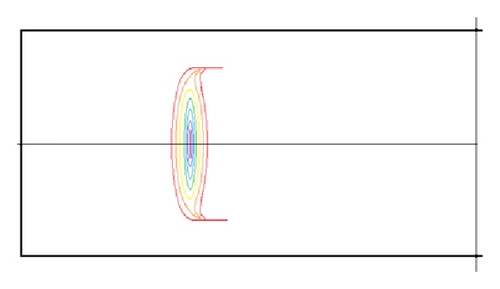
3.2. Numerical Results and Discussions

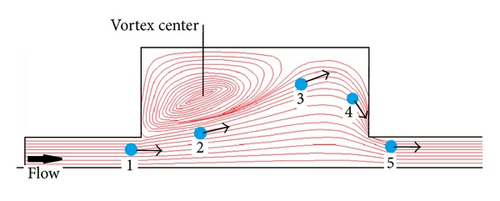
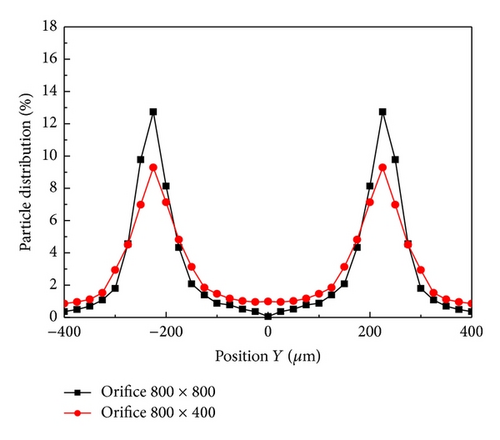
The channel geometry influences the particle trapping efficiency obviously. The main influence factors are aspect ratio, orifice number, and orifice structure. Figure 3 showed us that the aspect ratio affects the particle distribution obviously. Fortunately, the AR value of normal microfluidic device made of PDMS (polydimethylsiloxane) is bigger than 3. However, orifice number will also influence the trapping efficiency. Figure 5 shows us the contour lines of particle concentration in varying position of our device. Figure 5(a) is near the inlet but well developed, most of the particles were not trapped, and the particles distribution is almost identical over the entire section. At the end of first, second, and third orifices, the width of particle distribution decreases obviously in turn, and the particles near front and back wall fast disappeared. Near the channel end (outlet), the particles distribution appears to be two narrow lines. We also numerically simulated two orifice structures, and the comparison of their particle distributions (defined as the local population of particles to the total population of particles) was illustrated in Figure 6. Obviously the particles distribution lines in 800 × 400 μm orifice are not so narrow as those in 800 × 800 μm orifice. The reason should be that the particles trajectory will not be influenced by the microvortex in 800 × 400 μm orifice so greatly as that in 800 × 800 μm orifice. We can see in Figure 4 that the streamlines should be flat near the region from expansion to contraction when the orifice width decreased, and the particle movement at position 3 will not be so steep that the outward migration velocity is decreased.

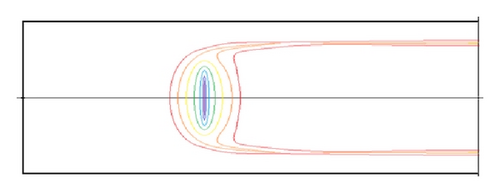
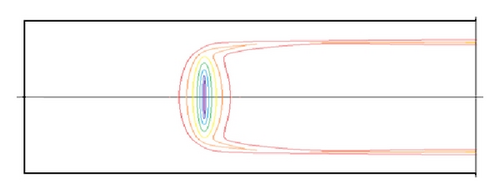
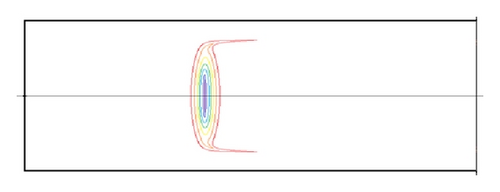
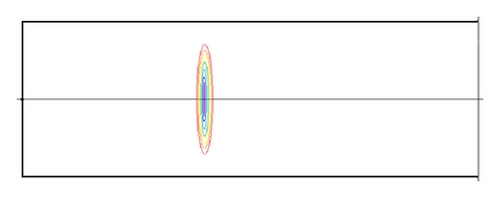
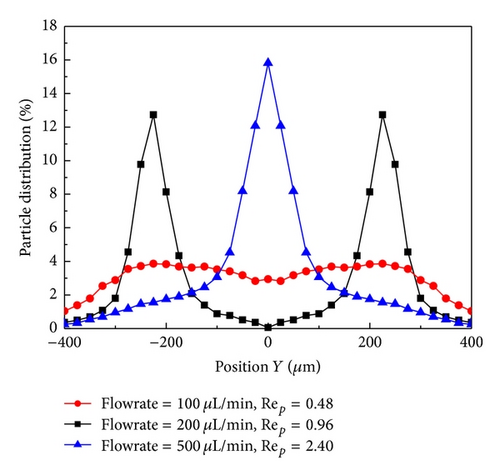
Equation (5) indicated that the flow rate is of great importance to the particle trapping. Our simulations were carried out for various flow rates ranging from 50 to 1000 μL/min, with relevant Reynolds number being about 8–160. To the particle size of 2, 7, and 15 μm, particle Reynolds numbers are calculated to be 0.02–0.41, 0.24–4.82, and 1.13–20.1, respectively. Figure 7 shows us the particle contributions in flow rates being 100, 200, and 500 μL/min, respectively, and the particle size is 7 μm. We can see that the trapping efficiency was better under the flow rate being 200 μL/min than that of 100 μL/min flow rate, and (5) indicated also that the lateral migration velocity (meaning of trapping efficiency) increased with the increasing of the flow velocity. However, almost all the particles concentrated near the center line of the channel, and the trapping efficiency closed to zero when the flow rate is very great. This can be explained as follows: when the flow velocity is great enough, the vortex center drifted right (see in Figure 4) and occupied almost the entire orifice, and therefore the streamlines in main channel will close to straight lines and the lateral migration of particles transverse to fluid streamlines decreased. In fact, Re_p can express the trapping efficiency, because we know that when Re_p is bigger than one, the inertial force becomes a dominant parameter for driving the lateral migration of particle transverse to fluid streamlines. In contrast, in the case of Re_p less than one, the particle behavior is strongly promoted to follow the flow pattern by a viscous drag force acting on the particle surface.

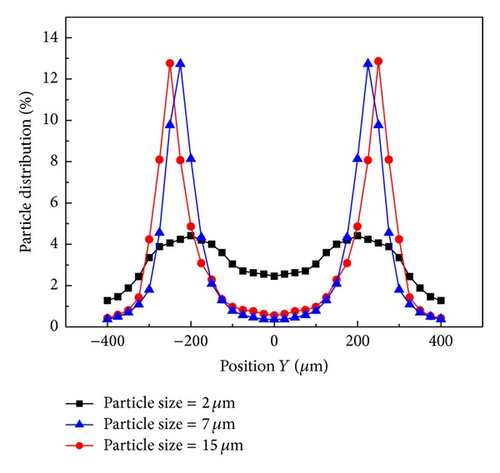
Particle size is another important factor to influence particle trapping efficiency. We simulated 3 sizes of particles 2, 7, and 15 μm, and the particle concentrations are 100, 25, and 5 × 10³/μL, respectively. In order to acquire relatively better trapping efficiency, the corresponding flow rate is 1000, 200, and 50 μL/min. The particle Reynolds numbers can be calculated using (6), and they are 0.41, 0.98, and 1.13, respectively. Although the particle Reynolds number is only 0.41 to particle size 2 μm, the flow rate is somewhat greater (1000 μL/min). The numerical results are shown in Figure 8. The particle distribution for particle sizes 7 and 15 μm showed us good trapping efficiency. Notice that the distribution center of particles with size of 7 μm is about 230 μm and that of particle with size of 15 μm is a little bigger (240 μm). However, the distribution center of particle with size of 2 μm is less than 210 μm. This result agrees with many published results. In addition, the numerical results verified once again that particle Reynolds number can predict the particle trapping efficiency.

4. Conclusions

After numerical simulations being carried out for various particle sizes under various flow rates in various orifices structures, the following conclusions can be drawn.

(1)
multiorifices structure is beneficial to particle trapping.
(2)
Aspect ratio of square channel influences the particle distribution greatly. When aspect ratio is bigger than 3, particle distribution appears to be two-lines structure, and loop line structure for less than 2 aspect ratios.
(3)
Particle Reynolds number is of great importance to particle trapping. When Re_p is bigger than one, the inertial force is dominant and enhanced the lateral migration of particle transverse to fluid streamlines. In contrast, in the case of Re_p less than one, the particle is to follow the flow pattern by a viscous drag force on the particle surface.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The author acknowledges the support from the Natural Science Foundation of Zhejiang Province China (LY12A02007).

References

1 Bao F. B. and Lin J. Z., Linear stability analysis for various forms of one-dimensional Burnett equations, International Journal of Nonlinear Sciences and Numerical Simulation. (2005) 6, no. 3, 295–303.
10.1515/IJNSNS.2005.6.3.295
Web of Science® Google Scholar
2 Bao F. B., Lin J. Z., and Shi X., Burnett simulation of flow and heat transfer in micro Couette flow using second-order slip conditions, Heat and Mass Transfer. (2007) 43, no. 6, 559–566, 2-s2.0-33847228085, https://doi.org/10.1007/s00231-006-0134-6.
10.1007/s00231-006-0134-6
Web of Science® Google Scholar
3 Bao F. B. and Lin J. Z., Burnett simulation of gas flow and heat transfer in micro Poiseuille flow, International Journal of Heat and Mass Transfer. (2008) 51, no. 15-16, 4139–4144, 2-s2.0-45449083611, https://doi.org/10.1016/j.ijheatmasstransfer.2007.12.009, ZBL1148.80306.
10.1016/j.ijheatmasstransfer.2007.12.009
CAS Web of Science® Google Scholar
4 Bao F. B. and Lin J. Z., Burnett simulations of gas flow in microchannels, Fluid Dynamics Research. (2008) 40, no. 9, 679–694, 2-s2.0-49549084362, https://doi.org/10.1016/j.fluiddyn.2008.03.003, MR2445866, ZBL1143.76057.
10.1016/j.fluiddyn.2008.03.003
Web of Science® Google Scholar
5 SooHoo J. R., Herr J. K., Ramsey J. M., and Walker G. M., Microfluidic cytometer for the characterization of cell lysis, Analytical Chemistry. (2012) 84, no. 5, 2195–2203, https://doi.org/10.1021/ac202461h.
10.1021/ac202461h
CAS PubMed Web of Science® Google Scholar
6 Kang J. H., Krause S., Tobin H., Mammoto A., Kanapathipillai M., and Ingber D. E., A combined micromagnetic-microfluidic device for rapid capture and culture of rare circulating tumor cells, Lab on a Chip. (2012) no. 12, 2175–2182, https://doi.org/10.1039/c2lc40072c.
10.1039/c2lc40072c
PubMed Web of Science® Google Scholar
7 Moon H. S., Kwon K., Hyun K. A. et al., Spatially gradated segregation and recovery of circulating tumor cells from peripheral blood of cancer patients, Biomicrofluidics. (2013) 7, no. 3, 034109, https://doi.org/10.1063/1.4808456.
10.1063/1.4808456
PubMed Web of Science® Google Scholar
8 Bhagat A. A. S., Bow H., Hou H. W., Tan S. J., Han J., and Lim C. T., Microfluidics for cell separation, Medical and Biological Engineering and Computing. (2010) 48, no. 10, 999–1014, 2-s2.0-77957818026, https://doi.org/10.1007/s11517-010-0611-4.
10.1007/s11517-010-0611-4
PubMed Web of Science® Google Scholar
9 Jiang D., Sun D. K., Xiang N., Chen K., Yi H., and Ni Z., Lattice Boltzmann numerical simulation and experimental research of dynamic flow in an expansion-contraction microchannel, Biomicroflidics. (2013) 7, no. 3, 034113, https://doi.org/10.1063/1.4812456.
10.1063/1.4812456
PubMed Web of Science® Google Scholar
10 Bălan C. C. M., Broboană D., and Bălan C., Lattice Boltzmann numerical simulation and experimental research of dynamic flow in an expansion-contraction microchannel, Microfluidics and Nanofluidics. (2012) 13, no. 5, 819–827, https://doi.org/10.1007/s10404-012-1005-8.
10.1007/s10404-012-1005-8
CAS Web of Science® Google Scholar
11 Karimi A., Yazdi S., and Ardekani A. M., Hydrodynamic mechanisms of cell and particle trapping in microfluidics, Biomicrofluidics. (2013) 7, no. 2, 021501, https://doi.org/10.1063/1.4799787.
10.1063/1.4799787
CAS PubMed Web of Science® Google Scholar
12 Tsai C. H., Chen H. T., Wang Y. N., Lin C., and Fu L., Capabilities and limitations of 2-dimensional and 3-dimensional numerical methods in modeling the fluid flow in sudden expansion microchannels, Microfluidics and Nanofluidics. (2007) 3, no. 1, 13–18, 2-s2.0-33947637219, https://doi.org/10.1007/s10404-006-0099-2.
10.1007/s10404-006-0099-2
Web of Science® Google Scholar
13 Tsai C. H., Yeh C. P., Lin C. H., Yang R., and Fu L., Formation of recirculation zones in a sudden expansion microchannel with a rectangular block structure over a wide Reynolds number range, Microfluidics and Nanofluidics. (2012) 12, no. 1–4, 213–220, 2-s2.0-84856210965, https://doi.org/10.1007/s10404-011-0864-8.
10.1007/s10404-011-0864-8
Web of Science® Google Scholar
14 Tsai C. H., Lin C. H., Fu L. M., and Chen H. C., High-performance microfluidic rectifier based on sudden expansion channel with embedded block structure, Biomicrofluidics. (2012) 6, no. 2, 024108, https://doi.org/10.1063/1.4704504.
10.1063/1.4704504
PubMed Web of Science® Google Scholar
15 Park J. S., Song S. H., and Jung H., Continuous focusing of microparticles using inertial lift force and vorticity via multi-orifice microfluidic channels, Lab on a Chip. (2009) 9, no. 7, 939–948, 2-s2.0-62649161487, https://doi.org/10.1039/b813952k.
10.1039/B813952K
CAS PubMed Web of Science® Google Scholar
16 MacH A. J., Kim J. H., Arshi A., Hur S. C., and Di Carlo D., Automated cellular sample preparation using a centrifuge-on-a-chip, Lab on a Chip. (2011) 11, no. 17, 2827–2834, 2-s2.0-80051625833, https://doi.org/10.1039/c1lc20330d.
10.1039/c1lc20330d
CAS PubMed Web of Science® Google Scholar
17 Hur S. C., Mach A. J., and Di Carlo D., High-throughput size-based rare cell enrichment using microscale vortices, Biomicrofluidics. (2011) 5, no. 2, 2-s2.0-79959913850, https://doi.org/10.1063/1.3576780, 022206.
10.1063/1.3576780
CAS PubMed Web of Science® Google Scholar
18 Lee M. G., Choi S., and Kim H. J., Inertial blood plasma separation in a contraction-expansion array microchannel, Applied Physics Letters. (2011) 98, 253702–253712, https://doi.org/10.1063/1.3601745.
10.1063/1.3601745
CAS Web of Science® Google Scholar
19 Lee M. G., Choi S., and Park J. K., Inertial separation in a contraction-expansion array microchannel, Journal of Chromatography A. (2011) 1218, no. 27, 4138–4143, 2-s2.0-79958851303, https://doi.org/10.1016/j.chroma.2010.11.081.
10.1016/j.chroma.2010.11.081
CAS PubMed Web of Science® Google Scholar
20 Buongiorno J., Convective transport in nanofluids, Journal of Heat Transfer. (2006) 128, no. 3, 240–250, 2-s2.0-33645634748, https://doi.org/10.1115/1.2150834.
10.1115/1.2150834
Web of Science® Google Scholar
21 Murshed S. M. S., Tan S. H., and Nguyen N. T., Temperature dependence of interfacial properties and viscosity of nanofluids for droplet-based microfluidics, Journal of Physics D. (2008) 41, no. 8, 2-s2.0-42549170489, https://doi.org/10.1088/0022-3727/41/8/085502, 085502.
10.1088/0022-3727/41/8/085502
Google Scholar
22 Matas J. P., Morris J. F., and Guazzelli E., Inertial migration of rigid spherical particles in Poiseuille flow, Journal of Fluid Mechanics. (2004) 515, 171–195, 2-s2.0-5444234134, https://doi.org/10.1017/S0022112004000254, ZBL1130.76301.
10.1017/S0022112004000254
Web of Science® Google Scholar
23 Zeng L., Balachandar S., and Fischer P. J., Wall-induced forces on a rigid sphere at finite Reynolds number, Journal of Fluid Mechanics. (2005) 536, 1–25, 2-s2.0-23844446089, https://doi.org/10.1017/S0022112005004738, ZBL1102.76017.
10.1017/S0022112005004738
Web of Science® Google Scholar
24 Chun B. and Ladd A. J. C., Inertial migration of neutrally buoyant particles in a square duct: an investigation of multiple equilibrium positions, Physics of Fluids. (2006) 18, no. 3, 2-s2.0-33645464069, https://doi.org/10.1063/1.2176587, 031704.
10.1063/1.2176587
CAS Web of Science® Google Scholar
25 Park J. S. and Jung H., Multiorifice flow fractionation: continuous size-based separation of microspheres using a series of contraction/expansion microchannels, Analytical Chemistry. (2009) 81, no. 20, 8280–8288, 2-s2.0-70449893812, https://doi.org/10.1021/ac9005765.
10.1021/ac9005765
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Hydrodynamic Trapping of Particles in an Expansion-Contraction Microfluidic Device

Abstract

1. Introduction

2. Problem Description