Optimising response to an introduction of African swine fever in wild pigs
Abstract
African swine fever virus (ASFv) is a virulent pathogen that threatens domestic swine industries globally and persists in wild boar populations in some countries. Persistence in wild boar can challenge elimination and prevent disease-free status, making it necessary to address wild swine in proactive response plans. In the United States, invasive wild pigs are abundant and found across a wide range of ecological conditions that could drive different epidemiological dynamics among populations. Information on the size of the control areas required to rapidly eliminate the ASFv in wild pigs and how this area should change with management constraints and local ecology is needed to optimize response planning. We developed a spatially explicit disease transmission model contrasting wild pig movement and contact ecology in two ecosystems in Southeastern United States. We simulated ASFv spread and determined the optimal response area (reported as the radius of a circle) for eliminating ASFv rapidly over a range of detection times (when ASFv was detected relative to the true date of introduction), culling capacities (proportion of wild pigs in the culling zone removed weekly) and wild pig densities. Large radii for response areas (14 km) were needed under most conditions but could be shortened with early detection (≤ 8 weeks) and high culling capacities (≥ 15% weekly). Under most conditions, the ASFv was eliminated in less than 22 weeks using optimal control radii, although ecological conditions with high rates of wild pig movement required higher culling capacities (≥ 10% weekly) for elimination within 1 year. The results highlight the importance of adjusting response plans based on local ecology and show that wild pig movement is a better predictor of the optimal response area than the number of ASFv cases early in the outbreak trajectory. Our framework provides a tool for determining optimal control plans in different areas, guiding expectations of response impacts, and planning resources needed for rapid elimination.
1 INTRODUCTION
African swine fever virus (ASFv) is a virulent pathogen of swine that has severe global socio-economic impacts (Brown et al., 2021; Mason-D'Croz et al., 2020; Tian & von Crame-Taubadel, 2020). Some strains cause near 100% mortality (Brown & Bevins, 2018). A detection in either wild or domestic swine triggers immediate control actions including movement and import-export bans, depopulation and disposal of affected swine and a need for increased surveillance capacity. As the range of ASF has expanded, it has become a major animal health and food security concern for many countries. As with other diseases at the wildlife–livestock interface (e.g., Gortazar et al., 2015), the ability of ASFv to persist endemically in widespread populations of wild swine (Sus scrofa) causes a major impediment for eradication efforts (Arias et al., 2018). Endemic persistence in wild swine obscures disease-free status and poses a re-introduction risk when a country eliminates ASFv from domestic swine. Additionally, control is more difficult to achieve in wild relative to domestic populations. Wild populations range freely, are usually not delineated, have movement processes and demographic ecology that are dynamic and change regionally, and disease surveillance is typically limited or non-existent. This makes it challenging to identify, locate and control infected individuals, which allows more opportunities for the disease to become established and spread across the landscape. These control challenges for an ASFv incursion have prompted many countries to develop plans for preventing an ASFv introduction in wild boar and wild pig populations and to rapidly respond if an introduction were to occur.
Recently, ASFv was detected in the Dominican Republic (FSN, 2021), which was the first time in almost 40 years the virus was detected in the Western Hemisphere. There is great concern that ASFv could enter the United States through contaminated pork products (Jurado et al., 2019) or other means (Brown et al., 2021). Following an incursion of ASFv in the continental United States, cumulative losses to the swine industry are predicted to be 50 billion USD (Carriquiry et al., 2020). The United States has a widely distributed wild pig population that occurs across different bioclimatic regions (McClure et al., 2015; N. P. Snow et al., 2017) and is sympatric with 37% of domestic swine farms (Miller et al., 2017). Wild pigs are an invasive species in the United States, and thus there is already substantial culling to control their damage at a national scale (Pepin et al., 2019) and a response plan to the potential introduction of the ASFv (USDA, 2020). The response area includes the initial establishment of a 5-km control area radius around wild pig detections within which intense culling and disease testing would occur in the wild pig population. The control area comprises two zones—the ‘infected zone’ minimum 3-km radius, ringed by the ‘buffer zone’ minimum of 2 km. A ‘surveillance zone’ minimum of 5 km is established around the border of the control area and, along with the buffer zone, is part of the ‘free area’. The response area is adaptive in that any new detections made from testing during the response would result in expanding the response area around each new detection based on the local wild pig movement characteristics and risk of disease transmission across the landscape (hereafter called ‘adaptive response’). Underlying ecological conditions can have a dramatic impact on wild pig space use and movement ecology (Gray et al., 2020; Kay et al., 2017), resulting in differences in rates and patterns of disease spread. Thus, it is important to investigate how ecological variation might influence the scale of the adaptive response during an outbreak.
To this end, we developed a spatially explicit model of ASFv transmission dynamics in wild pigs and determined the optimal response area (i.e., control + surveillance zone radius) by forward simulation and stakeholder-determined optimisation criteria. Our stakeholders included emergency response personnel from the US Department of Agriculture, Veterinary Services, who specified optimisation criteria during a structured discussion. In our previous work, we found that wild pig density, spatial structure and contact structure were key determinants of ASFv spread rates and establishment risk (Pepin et al., 2020, 2021; Yang, Boughton, et al., 2021). Thus, we investigated the effects of wild pig density and spatial ecology on the optimal response area with wild pig data from two different bioclimatic regions in the United States (fragmented rangeland and wetlands in Florida [FL] and mixed forest in South Carolina [SC]). We posed three main questions: (1) What size response area is needed to eliminate the ASFv in wild pigs as rapidly as possible? (2) How might the answer change with management constraints and local ecology? (3) When is it optimal to initiate culling from the outside or the inside of the culling zone? We hypothesized that the optimal response area would be, in part, driven by capacities for initial detection and culling. Specifically, we predicted that (1) if the initial detection of ASFv is quite long (months) after its introduction, a larger response area would be needed, and (2) if more wild pigs can be found and removed each day, a smaller response area could be optimal. We provide estimates of optimal response areas for different ecological and management conditions, explore their impacts on disease spread and illustrate what implementation of different response areas would mean for managers. Our approach addresses current gaps in spatial models of disease transmission in free-ranging animals and is readily extendable to other systems using data that are commonly collected (e.g., animal movement data).
2 MATERIALS AND METHODS
2.1 Approach overview
We developed a spatially explicit stochastic model of disease transmission based on ecological data from wild pigs in the United States and knowledge of ASFv disease dynamics. We simulated outcomes of disease spread under different management conditions and identified optimal response area sizes (determined from the radius around a positive case; hereafter referred to as the optimal control radius) for each set of conditions using criteria that were specified by our stakeholders (response personnel). For simplicity, we assumed that both intense culling and surveillance would occur throughout both the entire control area and surveillance zone (minimum 10-km radii). We then fit a regression tree ensemble model to the optimal control radii results with the management conditions as predictor variables. We used this model to evaluate how different management conditions determine optimal control radii and to generalize the results to other unmodelled conditions. Finally, we simulated how the application of optimal control radii impacted the outcome of disease spread and summarized the operational conditions that would be expected to occur when different optimal control radii are implemented. We conducted all analyses in Matlab version R2020b using the Statistics and Parallel toolboxes (MathWorks Inc.). Details of our analysis are further described below.
2.2 Disease transmission model
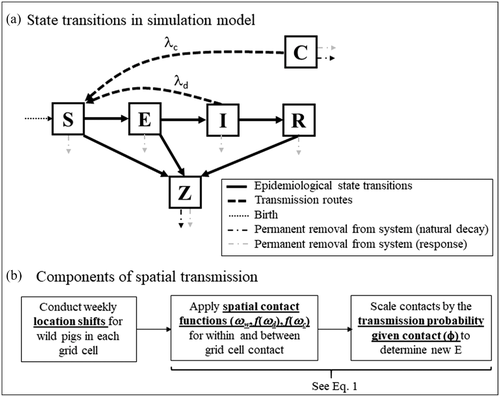
We modelled disease transmission using a stochastic metapopulation dynamics approach on a 50 × 50 km gridded landscape (2500 km2). The landscape was large enough that the ASFv spread under no control barely reached the outer edges by the end of the longest simulation (1.4 years) while maintaining a rapid run time for simulations. We used a compartmental model with the following state variables: susceptible (S), exposed (E), infectious (I), infectious carcass (C), non-infectious carcass (Z) and recovered (R) (Figure 1). Our previous work (Pepin et al., 2020) found that transmission from carcasses is likely to be substantial; thus, we included two modes of transmission: (i) between two living individuals (direct transmission) and (ii) between a living individual and a carcass (carcass-based transmission). We assumed that the disease-induced mortality was 95% to reflect the virulent strain that recently has been circulating in wild boar in Europe (Gallardo et al., 2017; Sanchez-Vizcaino et al., 2015). For wild pigs that survive, we assumed lifetime immunity because there are no data to support faster decay of immunity and because lifespan is probably short relative to immunity decay. The incubation and infectious periods of live individuals were random Poisson variables of 4 and 5 days on average, respectively (Pepin et al., 2020; Table 1). Carcass persistence on the landscape was fixed at 4.3 weeks, which is an average across different seasons (Table 1). We assumed that infectious and non-infectious carcasses were available for the same amount of time for contact or sampling and that for infected carcasses, infectiousness was constant throughout the carcass persistence period. Incubation, infectious and carcass persistence periods were converted to daily rates by taking their inverse and converted to probabilities (i.e., 1 − e–xt, where x is a rate per unit t) and then scaled to weekly probabilities. We modelled state transitions using a chain binomial model (Bailey, 1957). At the start of each simulation, the ASFv was introduced on Week 1 in one individual in the middle of the landscape. We excluded re-introductions.
| Parameter | Values | Source |
|---|---|---|
| Demographic parameters | ||
| Natural death rate | 0.0064 weeks−1 | N. S. Snow et al. (2020) |
| Birth rate | 0.0192 week−1 | Mean of Mayer and Brisbin (2009, fig. 1, p. 67) |
| Distance of weekly location shifts in kilometre | FL shifts ∼gamma(0.751, 0.355); SC shifts ∼ gamma(0.566, 1.91) | Fit data from Yang, Schlichting, et al. (2021) to a gamma distribution (Figure S4) |
| Initial density | 1.5, 3 or 5 wild swine/km2 | Varied; N. S. Snow et al. (2020) |
| Mean family group size at initiation | 2, 4 or 6 wild swine per grid cell depending on density (1.5, 3 or 5) | Expert opinion |
| Epidemiological parameters | ||
| Incubation period | ∼Poisson (4 days), truncated at 1 | Gallardo et al. (2017) |
| Infectious period | ∼Poisson (5 days), truncated at 1 | Gallardo et al. (2017) |
| Carcass persistence period | 4.3 weeks | Selva et al. (2005); Pepin et al. (2020) |
| Disease-induced mortality | 95% | Sanchez-Vizcaíno et al. (2015) and Gallardo et al. (2017) |
| Transmission rate within grid cells (direct and carcass-based): ωw | 0.74 (FL), 0.94 (SC) | Estimated from data in Yang, Schlichting, et al. (2021) using Equation (2) |
| Scaling parameter for transmission probability given contact among grid cells: ϕ | Varied by density and state where movement and contact data were collected: Direct FL: 0.9, 0.4, 0.2 for swine density of 1.5, 3 and 5; direct SC: 0.009, 0.004, 0.002 for swine density of 1.5, 3 and 5 Carcass-based (each condition): ϕ × 0.5 |
Sensitivity analysis; Figures S1 and S2 |
| Contact rate among grid cells (direct): f(ωd) | α = −0.80, β = −1.91 (FL) α = 0.64, β = −1.16 (SC) | Estimated from data from Yang, Schlichting, et al. (2021; Figure S3, top) using logistic regression; Equation (3) |
| Contact rate among grid cells (carcass-based): f(ωc) | α = 2.32, β = −6.37 (FL) α = 9.82, β = −4.11 (SC) | Estimated from data from Yang, Schlichting, et al. (2021; Figure S3, bottom) using logistic regression; Equation (3) |
| Culling parameters | ||
| Culling radius | 3–15 linear km (increments of 1 km) | Varied |
| Culling strategy | Start in or start out | Varied |
| Culling capacity | 2.5, 5, 7.5, 10, 15 or 20% of population in culling zone per week | Varied |
| Initial detection day (since introduction) | 8, 15 or 20 weeks | Varied |
| Scaling parameter on density-dependent capture probability: f(γ, density) | 1.1 | Expert opinion; see Figure S5 for functional form |
- Note: Parameters we varied to determine the optimal control radius are highlighted in light grey. We also varied whether the location shift and contact patterns were from low movement (FL; fragmented pasture and wetlands in Florida) or high movement (SC; mixed forest in South Carolina) areas.
2.3 Spatial transmission
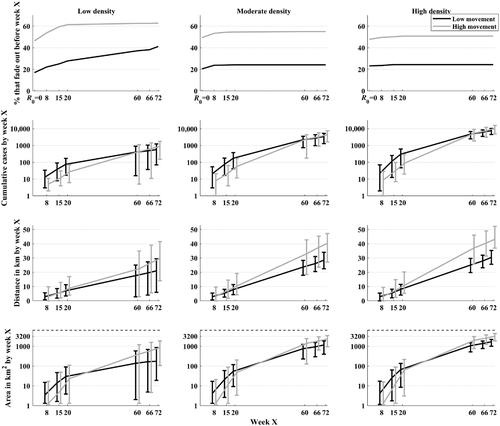
Three components are important for modelling spatial disease transmission in animals: 1) the amount of contact they make with others in their surrounding vicinity (contact rate; ω), 2) the transmission probability of ASFv when contact occurs (transmission probability given contact; ϕ), and 3) where animals currently are on the landscape at each time step (location shifts) (Figure 1, Table 1). Sub-populations within grid cells were assumed to be individuals from the same family group. We assumed that individuals within grid cells mixed homogenously, while groups among grid cells contacted each other at a frequency that depended on distance. We made these assumptions because previous work found that clustering of family groups influenced spatial disease transmission of the ASFv in wild pigs (Pepin et al., 2021; Podgorski et al., 2022). The force of infection (λ, Equation 1) included contact terms (ω) for within cells (w) and direct (d) or carcass-based (c) transmission between cells. The behaviour of spatial transmission in the absence of response is shown in Figure 2.
2.4 Contact among wild pigs in the same grid cell
We assume that within-cell contact rates (ωw) were equivalent among living individuals or between living individuals and carcasses and that these were also equivalent to a transmission rate (calculated from animal movement data as shown in Equation 2, where xw is the number of direct contacts per day for individuals in the same group, and Nw is the total number of possible contacts per day for individuals in the same group).
2.5 Contact among wild pigs between grid cells
Similarly, f(ω)k,j describes the spatial contact function for direct (d) or carcass-based (c) transmission between grid cells. Parameters for the spatial contact function (f(ω)k,j) were estimated using logistic regression (Equation 3) with distance (Xk,j) between median weekly location for pairs of individuals from different family groups as the predictor for direct contact and distance between median weekly location of individuals and food supplements as the predictor for carcass-based transmission (Figure S3). The models used animal contact and movement data from global positioning system (GPS) collars and proximity loggers affixed to wild pigs in our previous work (Yang, Boughton, et al., 2021; Yang, Schlichting, et al., 2021). We categorized the site differences in movement (Figure S1) and contact (Figure S2) as low versus high movement, where median weekly location shifts in low-movement pigs were 163 m (FL site) versus 526 m in high-movement pigs (SC site). The data analysis for estimating the contact functions and weekly location shift distribution parameters is described in the Supplementary Information sections ‘Estimating Location Shift Distributions from Animal Movement Data’ and ‘Estimating Spatial Contact Function’ and shown in Figures S1 and S2, respectively. Note that we used food supplements as point-source proxies for carcasses because we had no data on contact rates with carcasses and because wild boar can be attracted to and make contact with dead conspecifics (Probst et al., 2017).
2.6 Transmission probability given contact
2.7 Simulating weekly location shifts
We used a grid-cell size of 0.4 × 0.4 km for our landscape to approximate the scale at which wild pigs move across space at a weekly scale (Figure S1) because the majority of weekly location shifts in the data were < = 0.4 km, and this maintained reasonable computational time. To simulate weekly location shifts of groups among grid cells, we randomly selected a location shift distance for groups in each grid cell from the estimated gamma distribution (Table 1). For groups that selected shifts < 0.4 km, no location shift was made. For groups that selected shifts > 0.4 km, all other grid cells within an arbitrarily close distance to the selected distance were selected as potential new cells (the arbitrary distance was 0.1 km; e.g., if the selected distance was 0.8 km, all grid cells between 0.7 and 0.9 km from the current grid cell were selected as potential destinations). Of those potential destination cells, we selected the cell with the lowest abundance of wild pigs already present because different family groups typically remain independent (Kilgo et al., 2021; Sparklin et al., 2009). If there was a tie for cells with the lowest abundance, we selected among the tied cells at random.
2.8 Birth/death
Births (S only) occurred throughout the year (N. S. Snow et al., 2020) at a constant rate (Table 1) in a density-dependent manner following logistic population growth. Birth rates have seasonality that varies throughout the United States (Mayer & Brisbin, 2009; N. S. Snow et al., 2020), but exploring the effects of this seasonality was outside the scope of our current study. Carrying capacity was assumed to be 1.5 times the initial population abundance (Table 1) to allow populations to grow (i.e., substantially away from carrying capacity) at the start of simulations, as many populations in the United States appear to be growing (Pepin et al., 2019; N. P. Snow et al., 2017). The natural death rate was fixed and occurred in S, E and R individuals. We assumed an average lifespan of 3 years (Table 1) before dying of causes unrelated to ASFv or ASFv-response culling.
2.9 Response model
Responses were initiated when the initial detection day was reached (rationale in the Discussion section). We assumed that all individuals culled were also sampled for the ASFv with a turnaround time for test results of 1 day. We also assumed that response activities included both killing and removing living individuals and locating and removing carcasses and that these activities occurred at equal frequencies (i.e., in proportion to the presence of infectious individuals or carcasses) and required similar effort by personnel (because we did not have any data to assume otherwise). We applied an adaptive response area as specified in the current plan (USDA, 2020). Thus, any additional detections that were made based on testing in the response area resulted in an expansion of the area so that the response area radius extended from all detections.
Across simulations, we varied the following: the response area radius (3–15 km), the response strategy (whether the response started on the outside and worked out-to-in or the reverse), the weekly culling capacity (2.5%–20% of the population in the radius), the time since introduction that the first ASFv-positive wild pigs were detected (8, 15 or 20 weeks), the ecological context (low versus high movement) and the wild pig density (1.5, 3 or 5 per km2). These ranges were determined based on discussions with wild pig managers at USDA, Wildlife Services. We also assumed that culling success was density-dependent such that the proportion of the population that was actually captured depended on the remaining density in the response area according to the function in Figure S5. Thus, if the daily culling capacity was 10% of the population, close to that target would be culled daily when the wild pig density in the response area was 5 per km2 (i.e., 0.95 × 10% = 9.5%; Figure S5), whereas only about 5% would be removed when the wild pig density in the response area was 1 per km2 (i.e., 0.5 × 10% = 5%). We provide an example of how the combination of culling capacity and density-dependent capture success translates to weekly numbers of wild pigs removed and declines in abundance in Figure S6. We varied the response strategy (in-to-out versus out-to-in) by focusing on weekly culling at a given culling capacity consistently closest to the most recent detections (in-to-out) or closest to the outside edges (out-to-in) of the response area.
2.10 Simulation conditions
To initiate hosts on the landscape, we assumed that family group size was a Poisson random variable with a mean of 6 (based on one adult female with an average litter size of 5; N. S. Snow et al., 2020). We randomly selected family group sizes for assignment to unique grid cells until the total initial abundance was achieved. Thus, in lower density conditions, fewer grid cells were occupied than in higher density conditions. We simulated the spatial spread of the ASFv at a weekly scale for 1 year following a single introduction in the middle of the landscape. Home range shifts occurred weekly. We then introduced weekly culling at a fixed time (i.e., either 8, 15 or 20 weeks) after introduction. For each parameter set, we conducted replicate simulations, with more simulations conducted for the outbreak conditions that tended to cause natural fade-out early on (Figure 1; specifically: 800 for all low movement conditions; 1200 for high movement at low density; 1000 for high movement at moderate and high density). Example spatial dynamics produced by the model are shown in Figures S7 and S8.
2.11 Optimisation
We tracked the outcome of four key metrics of interest to stakeholders: maximum area of ASFv spread, maximum linear distance of ASFv spread from the index case, epidemic duration (total number of days there is at least one infected individual or carcass) and probability the strategy eliminates ASFv within a specified time frame (here, 1 year). We considered the optimal control radius and strategy to be the one that results in the lowest value for the average of all four metrics after rescaling each of them to a maximum value of 1 (i.e., placing them on equal scales) and giving them each equal weighting in the averaging. We selected all radii and strategies in the first percentile (lowest 1% of average scores) as the parameter sets that were optimal. We only included runs where there was at least one infectious individual or carcass at initial detection (i.e., R0> 0 with ≥ 1 infectious individual or carcass at detection). To determine the optimal control radii, we took the median of the distribution of optimal control radii for each set of conditions and displayed this with its 90% credible intervals to show uncertainty in the estimates. We chose 90% credible intervals instead of the more typical 95% level because distributions tended to be unimodal and left-skewed (i.e., there was a long tail towards lower values that occurred infrequently; extending the uncertainty to include more of this tail would reduce the lower bound towards conditions that suggest substantially lower optimal radii but actually occur infrequently and are driven by the stochastic nature of disease dynamics). To determine the optimal strategy (in-to-out versus out-to-in), we labelled culling in-to-out as a 1 and culling out-to-in as a 2. We then calculated the mean and 95% standard error for the strategy values that fell in the lower first percentile of the distribution of optimal radii. If the mean + SE was < 1.5, the optimal strategy was determined to be in-to-out. If the mean SE was > 1.5, the optimal strategy was determined to be out-to-in. Otherwise, both strategies were considered equally optimal.
2.12 Evaluating effects of management conditions on optimal radii
To understand how management, outbreak and ecological conditions (predictor variables) determine the optimal control radius, we developed a boosted regression tree (BRT) model (e.g., Elith et al., 2008). We chose a BRT approach for this analysis because the response variable followed a complex distribution (i.e., a non-parametric approach was better), and we expected higher-level interactions among predictors (i.e., which are naturally incorporated in BRT approaches). We used least-squares boosting as the ensemble aggregation method (fitrensemble function in Matlab; Mathworks, 2022) with four predictor variables: (A) culling capacity, (B) time between introduction and initial detection (detection week), (C) number of infected individuals at detection and (D) the movement type by density combination (a factor with six levels). (A) and (B) accounted for differences in management conditions. (C) accounted for stochastic differences among simulations in the number of infected individuals and carcasses at initial detection, which is an outcome of the simulation, not an input parameter. (D) represented differences in the ecological context (low versus high movement) and density, which together drive the rates of spatial spread in the absence of management. First, we determined the best predictive ensemble model using cross-validation. We exponentially increased the tree complexity level from one split to 2048 splits and increased the learning rate from 0.1 to 1 and fit regression tree ensembles of 150 trees under each set of hyperparameters. We identified the optimal hyperparameters (maximum number of splits, number of trees and learning rate) in the best BRT model by choosing hyperparameters that yielded the lowest overall 5-fold cross-validated mean-squared error. Finally, we trained our predictive BRT model using those chosen hyperparameters: 20 learning cycles (trees), 16 as the maximum number of splits, and a learning rate of 0.25 and estimated the predictor variable importance (Figure S9) under these conditions. Spearman's rank correlation between the simulated optimal radii and those predicted by fitting the BRT model to simulated data was 0.54. We used the model to predict optimal radii using a full-factorial design with our four predictor variables over the ranges used in the initial set of simulations.
2.13 Evaluating the impacts and operational dynamics of optimal radii and strategies
Finally, we conducted simulations with the optimal control radii/strategies under each set of management conditions to evaluate the effects on disease spread outcomes and what managers would be faced with in the field. For each set of management conditions, we conducted replicate simulations (800—all densities with low movement, 1200—low density and high movement, 1000—moderate and high density and high movement) with the estimated optimal radius (median of the optimal radii distribution) and strategy using the same number of replicate simulations as in the optimisation. To show the impacts of management, we tracked the number of weeks there were new cases after the initial detection day (duration), the maximum area of spatial spread in km2, and the furthest linear distance in km that an infection occurred relative to the true index case location. To show the operational dynamics that would be expected under each optimal control radius/strategy, we tracked the following: the maximum number of wild pigs in the culling zone, the total number of hosts culled to achieve ASFv elimination, the maximum area of the culling zone on any given week, the maximum number of positive detections within a week, the mean detection rate and the mean proportion of infected individuals or carcasses that occur within the response area. We summarized the simulation output descriptively as the median with 90% credible intervals.
3 RESULTS
3.1 Estimates of optimal control radii
On average, across all conditions, the optimal culling radius was 13.3 km (median = 14 km). Across all conditions, 90% of the values fell between 9 and 15 km (the highest value we examined), and 50% of the values fell between 12 and 15 km (Figure 3). The overall average optimal culling radius translates to an area of 556 km2. In the high movement condition, the median optimal radius was 15 km, with 90% of the values being between 12 and 15 km. In the low movement condition, the median optimal radius was 13 km, with 90% of the values being between 8 and 15 km. Lower optimal radii were possible at the highest culling capacities (medians of 12 and 14 km for low and high movement conditions across all density and detection weeks). Uncertainty in the optimal culling radius tended to be highest in the low movement condition when detection was early at 8 weeks (Figures 3 and 4). This was also the only condition where substantially lower optimal radii were observed at higher culling capacities (e.g., an average of 10.7 km at culling capacities ≥ 15% weekly, with 90% of the values falling between 6 and 15 km and a median of 11 km across all densities, and a median of 10 km for the moderate and high densities). In the low movement condition, the probability of elimination within 1 year was close to 100% for optimal radii across all conditions, but in the high movement condition, this only occurred at culling capacities near or above 10%, suggesting that radii above 15 km (i.e., more resources) may be needed when culling capacity is low. In the high movement condition, culling capacities > 10% weekly were important in general.
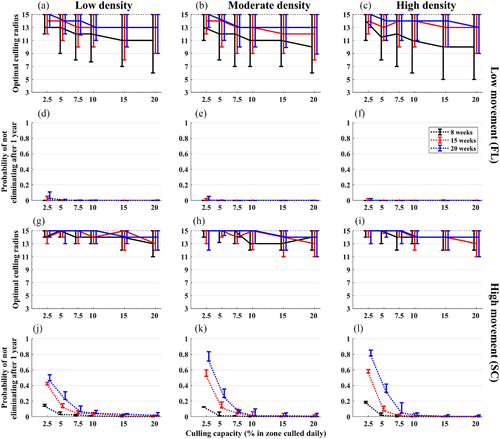
Our stakeholders concluded that constraining the optimisation by the amount of effort expended was not of interest because the priority would be to eliminate the ASFv as rapidly as possible regardless of costs. However, when the optimal radius was defined not only as the one that minimized ASFv duration and spatial spread but also minimized the number of wild pigs that needed to be removed to achieve elimination, substantially lower optimal radii were identified, especially under low movement, high culling capacities (≥ 15%), moderate to high densities and early detection (8 weeks; Figure S10). Under those conditions, 90% of the optimal radii were between 5 and 11 km with a median of 7 km (Figure S10). However, the average over all conditions was similar to when the effort was not used to constrain the optimisation—12.8 km, with 90% of the values falling between 8 and 15 km and a median of 14 km. Additionally, for the high movement condition, even when detection was early at 8 weeks, culling capacities ≥ 15%, optimal radii were still quite large, with a median of 13 km across all densities and 90% of the values being between 10 and 15 km. This was only slightly lower than when the effort was not used to constrain the optimisation (median 14 km with 90% of values between 12 and 15 km). Both of these resulted in a near 100% probability of ASFv elimination within 1 year.
Our optimisation algorithm selected optimal radii over both the radius and strategy dimensions. It was always better to prioritize culling closest to the most recent detection (in-to-out strategy), then to prioritize culling towards the outside edge and work out-to-in (data not shown).
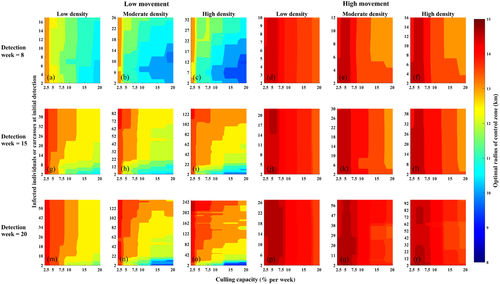
3.2 Predictors of optimal control radii
The most important predictor was the movement type by density condition (Figures 4 andS8). Detection week was the next most important predictor of optimal culling radius, followed by the number of infected individuals/carcasses at detection and culling capacity. The number of infected individuals/carcasses at detection correlates with early epidemic growth metrics such as R0, whereas the movement type correlates with the rate of spatial spread. Our results showed that the rate of spatial spread was far more important for predicting optimal response area sizes relative to early epidemic growth metrics (Figure 4). In the high movement condition, optimal radii were mostly affected by culling capacity, and this effect was marginal (ranging from 13 to 15 km only, with 13 km only observed at moderate-high densities, detection Week 8, and culling capacities ≥ 15%). A broader range of optimal control radii was predicted under the low movement conditions, where the optimal radii also depended on the number of infected individuals or carcasses at initial detection (Figure 4). In general, optimal radii as low as 10 km could be used when the number of infections at detection was roughly 10 or lower and the culling capacity was 15% or higher.
3.3 Impacts of culling on disease dynamics
In low movement conditions with initial detection at week 20, duration was reduced from 52 weeks (cut-off of the simulations) under no control to between 3 and 7 weeks with upper limits of between 6 and 18 weeks (for higher to lower culling capacities ranging from 5% to 20%; Figure 5a–c). In the same condition with high movement, applying the optimal radii resulted in ASFv elimination between 4 and 21 weeks depending on culling capacity (ranging from 20% to 5%), with upper limits of duration ranging from 15 to 52 weeks after detection (end of the simulation). Culling capacities of only 2.5% per week were generally less effective at reducing the duration or spatial spread, especially under the high movement conditions, and in the high movement conditions, culling capacities of ≥ 10% were needed to reduce the upper limits of duration below the full 52 weeks. The effects of optimal radii and culling capacity were similar on spatial spread—culling capacities of 10% or higher were needed to cause substantial reductions in spatial spread under high movement, while culling capacities of 5% or higher caused substantial reductions in spatial spread relative to no control under the low movement conditions. In general, when the lower bounds of the optimal radii were used in simulations, duration and spatial spread were not as reduced (Figure S11), suggesting that the medians and upper bounds of optimal radii are more conservative. The best outcomes were observed when detection was early at 8 weeks (Figure S12), which was especially important for high movement conditions.
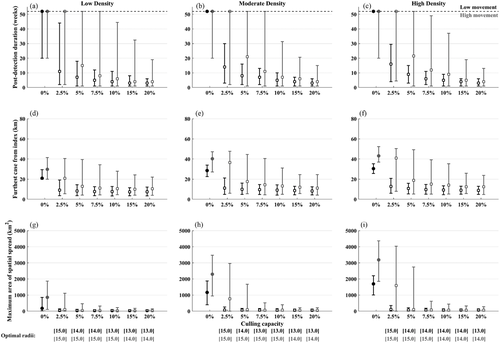
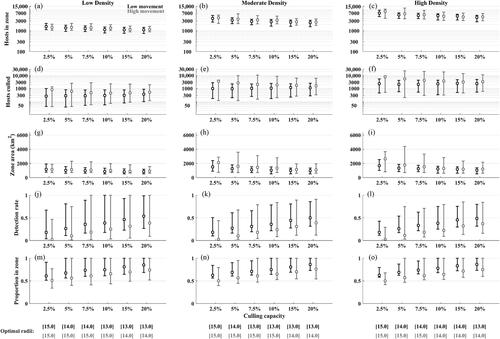
3.4 Operational dynamics during the application of optimal control radii
We examined the operational dynamics using the same output as with the culling impact analyses. Most commonly, the maximum number of hosts in the culling zone was 2759 (90% bounds: [1111; 6543], all intervals that follow are 90% bounds) under low movement conditions and 3295 [1159; 7762] under high movement conditions (Figure 6). The total number of wild pigs culled to reach elimination was most commonly 1037 [263; 2455] under low movement and 1963 [1159; 7762] under high movement. The maximum zone area during adaptive response was 1080 km2 [840; 1613] under low movement and 1196 km2 [899; 2432] under high movement. Figure 6j–k shows the important relationship between culling capacity and average detection rate, with median detection rates below 25% when culling capacity is 5% or lower but near 50% when culling capacity is 20%. Similarly, the average proportion of infected individuals who occur inside the response area can be as low as 50%–55% at low culling capacity but increases towards 100% at 20% culling capacity (Figure 6m–o).
4 DISCUSSION
We examined optimal response area sizes across a range of realistic ecological conditions for wild pigs in the United States. Our analyses underscore the importance of considering local ecology when planning a response to the ASFv. The higher rates of between-group contact and farther distance of weekly movement in the high-movement pig population translated to strikingly higher rates of spatial spread of ASFv and a need for larger response areas. In addition to affecting the epidemiological characteristics of ASFv, local ecology can affect operational response activities such as culling capacities because differences in vegetation, topography or road density (for access with heavy trapping equipment) can influence the ability to locate and remove wild pigs (Davis et al., 2018). Thus, accounting for local ecology and realistic culling capacities will be important when defining region-specific guidelines for optimal response areas.
The optimal size of the response area was much larger under ecological conditions that promoted higher rates of spatial spread, regardless of the early epidemic incidence rates. Thus, a second major implication of our findings is that R0 or early outbreak incidence rates may not be the best guidance for planning control radii or culling capacity. While the low movement conditions led to more cases in the first 20 weeks relative to the high movement conditions, larger control radii and higher culling capacities were needed to control ASFv under the high movement conditions. This contrasts with the theory developed for non-spatial disease spread, which predicts that higher intensities of control are needed in populations with higher R0 (Anderson & May, 1982) and highlights the importance of considering other epidemiological metrics for planning control in spatial settings (Tildesley & Keeling, 2009). In the case of ASFv in wild pigs, the high movement condition requires a higher culling capacity and larger control radii to contain the spread to increase the chances of locating infected individuals who may be quite far from the initial detection (Figure S7). In the low movement conditions, the outbreak spreads more like a diffusion process, with a lower chance of long-distance dispersal of the disease, and thus detection can be efficient even with lower culling capacities (Figure S6). These differences emphasize the importance of understanding how wild pigs use different landscapes, including during dispersal, for predicting where ASFv is most likely to spread and what response area size and culling capacity are optimal in different ecoregions.
4.1 Management implications
Most conditions we examined suggested that the optimal control radius should be at least 14 km. In conditions with high movement, our analyses suggested that larger radii could be important, although we did not explore radii above 15 km or culling capacities above 20% weekly because they are very difficult to achieve in practice. Only when high culling capacities can be achieved (≥ 15% of the population weekly) and under low-movement conditions did we observe that control radii < 14 km could be adequate. A key reason is that by the time initial detection occurs in high movement conditions, there are likely multiple distinct and distant foci of ASFv transmission. In our model, we assumed that surveillance data were coming only from individuals and carcasses that were removed through management activities in the response area. However, if after an initial detection there is also enhanced active surveillance outside the response area (as would be the case), these other foci might be found more rapidly (relative to relying only on the expansion of the initial control area), leading to additional control areas and more rapid elimination of ASFv. Under these conditions, it could be possible to use smaller control radii as long as a fairly large zone of enhanced surveillance are used around all foci. Under the parameters we used, the ASFv in high-movement wild pigs travelled 9–11 km from the index case by Week 20 and 22–37 km by week 60, depending on density, which is close to that observed in European wild boar (EFSA et al., 2018; Podgorski & Smietanka, 2018). Thus, depending on when initial detection occurs relative to the true index case, the surveillance zone may need to be very large (EFSA et al., 2018), and the size should depend on population density and delay in detection, applying larger surveillance zones in higher density areas. Previous work suggested that a radius extending at least 50 km from the middle of the core control area that allows intensive hunting is important for the containment in wild boar (Lange, 2015).
Application of the optimal, adaptive control radius in the high-density and high-movement conditions may require removal of more than 22,000 wild pigs within a zone area that had expanded to more than 4400 km2 (e.g., Figure 6), which is equivalent to a response area radius of 37.4 km. Response areas of this size can result in significant logistical and resource challenges that increase the time to elimination. A significant number of personnel and equipment resources would be needed, especially in areas where trapping and ground shooting might be the only effective control tools. An additional logistical constraint is the number of landowners that may be impacted. In many areas, working in such large response areas will likely require coordination from many landowners, including private landowners, and gaining this cooperation in a timely manner will be important for rapid elimination.
Other types of delays that we did not account for included the time between initial detection and ramping up the response to full capacity. For example, if the culling capacity was 20%, we assumed that 20% of the population was removed in the first week following detection. However, it is likely that there would be a lag in reaching full culling capacity. There could be extremely challenging field conditions in the response area that limit culling capacity, delay times between collection of surveillance data and case confirmation, legal complications due to private land access, other disease control or agriculture protection priorities that divert resources, or obstacles in the stockpile and supply chain for distributing the necessary control resources as rapidly as possible (Miguel et al., 2020). Additionally, in other disease control events, removal of large numbers of carcasses can be logistically challenging, resulting in a slowdown of culling processes or extension of the time that infectious carcasses are available for contact by susceptible individuals. In our model, we assumed that when individuals were culled or carcasses removed, they were instantaneously disposed and no longer available for transmission. It could be interesting to explore the trade-off between a response that involves time-intensive carcass disposal with reduced environmental contamination versus one that leaves carcasses in place and is thus able to remove more individuals more quickly. We also did not model the potential for response personnel to contaminate the area or translocate infection outside it. Given these potential challenges, it is likely that our estimates of optimal radii, time to elimination, and operational outcomes are conservative and lower than would be needed in reality.
The most important determinant of the optimal radius was the movement type by density condition. This was because in the high movement condition, the ASFv spread in a characteristically different way than in the low-movement condition. Thus, it could be important to apply different strategies for delineating the response area depending on the movement characteristics of the host population that may be informed by local density and environmental conditions. In high-movement conditions, the best strategy may be to focus initially on finding all the foci by applying intensive surveillance at farther distances from detections, while culling intensively close to each detection. However, in the low-movement condition, a single adaptive response area that focuses all response resources closest to the most recent detection was generally sufficient to encompass the infected area. The decision of which strategy to apply (emphasising intense surveillance outside the control area or not) could be informed by the rate at which new cases are confirmed at farther distances in the control area early in the response. This plan aligns with other frameworks that call for adaptive responses to control outbreaks and conduct surveillance to improve the management of diseases (Miller & Pepin, 2019).
4.2 Model strengths, limitations and future directions
There are several methods for modelling spatial disease transmission (White et al., 2018). We take a metapopulation approach where subpopulations represent family groups, and family groups can move to open or low-density patches during dispersal or resource tracking (following available food resources). A widespread gap in spatial transmission models has been due to a lack of accounting for the potential for disease transmission along animal movement trajectories or even a lack of modelling host location changes altogether (i.e., modelling the spread of disease through a population with fixed host locations). A strength of our approach is that we account for realistic frequencies that host groups move among patches and how far they move during each location shift. This allows different host groups to contact one another more regularly as they move throughout the landscape, rather than having a static surrounding population for contact. Thus, our model implicitly accounts for the dynamic nature of contact due to changing environmental conditions and host life history.
Our study focused on wild pig movement and contact behaviour from two different ecosystems in the United States, but a wider range of movement and contact behaviour is possible across the United States (Gray et al., 2020; Kay et al., 2017; Pepin et al., 2016), driven largely by environmental conditions. However, in our model, wild pig movement and contact were determined from GPS-tracked adult wild pigs, but we did not explicitly link movements to environmental conditions. Rather, we assumed that all individuals moved and contacted each other according to the same movement and contact distributions across the entire study area (a homogeneous landscape), which could lead to faster rates of spatial spread in landscapes that are less permissive to movement. Thus, we did not account for individual-level variation in movement and contact or changes in these processes across the landscape (environmentally determined variation or sex differences). Accounting for environmentally determined variation in movement and contact among individuals can improve inference of the spatio-temporal dynamics of disease spread on landscapes (Wilber et al., 2022), suggesting that it is likely important to allow movement and contact to change with landscape features within the study area for making more accurate predictions of spatial spread. Linking movement and contact to the environmental context would also provide a mechanism for predicting ASFv spread in different landscapes (Manlove et al., 2022) without relying on GPS data from every landscape where prediction is needed. These advancements in our disease simulation model could improve its accuracy in a variety of environmental contexts across the United States.
We also assumed that wild pig movement behaviour would remain similar during intense control activities as it is in the absence of these activities. However, even for much less intense control levels than would occur during an ASFv response, changes to movement speed and habitat selection occur in some individuals (Bastille-Rousseau et al., 2021; Campbell et al., 2010; Fischer et al., 2016). Also, wild pigs are social animals that potentially will travel long distances to reconnect with conspecifics when their family group members are removed (unpublished data). Thus, both physiological stress and social disruption that may occur during intense control activities could cause changes in the movement behaviour of wild pigs during control that affect the spatial spread of the ASFv. This potential effect has been observed for Mycobacterium bovis in badgers, another social species, where intense culling resulted in increased ranging and further disease spread (Woodroffe et al., 2006). A better understanding of how the movement and contact behaviour of wild pigs respond to intense control is needed to predict its potential effects on the spatial spread of the ASFv during a response.
While most wild pig movement is localized and occurs naturally, wild pigs are also translocated by humans over longer distances (Bevins et al., 2014; Hernandez et al., 2018; Tabak et al., 2017). Our model did not account for translocation, which can occur frequently in some populations (Tabak et al., 2017) or natal dispersal (our GPS collars were all on adults). Natal dispersal has been documented in Sweden as 4.5 km for females and 16.6 km for males on average (Truve & Lemel, 2003), but few data on dispersal distances were available from our sites. Translocation could result in a much farther spread of the ASFv than expected, highlighting the importance of policies and public education campaigns to reduce the anthropogenic movement of wild pigs. Other potential mechanisms of long-distance spread could be from avian scavengers or large carnivores that disperse infectious carcass material (Vincente & VerCauteren, 2019), but these potential routes are poorly understood for the ASFv. Repeated introduction from infected domestic pig farms is another mechanism affecting the spatial patterns of cases that we did not include. This interface could be especially important in areas with numerous small enterprise domestic pig farms where biosecurity might be low, allowing contact with wild pigs (USDA, 2009, 2014). In some European countries, the ASFv may transmit separately within wild boar and domestic pigs, occasionally spilling back and forth at this interface and generating distant, distinct infection foci (Alvarez et al., 2019; Arias et al., 2018; Frant et al., 2020). Accounting for the potential for small enterprise domestic pig farms to contribute to the spatial dynamics of the ASFv in wild pigs could be important for refining predictions of disease spread in some landscapes. Excluding long-distance spreading processes and reintroductions when planning response areas could lead to underestimation of the response areas and longer persistence than predicted by our model, as has been observed in other countries (e.g., Danzetta et al., 2020).
Transmission from carcasses is thought to play an important role in the transmission and persistence of ASFv in wild boar (Gervasi & Guberti, 2021; Lange & Thulke, 2017; Pepin et al., 2020). Data from Europe suggest that the ASFv can persist for weeks or months in carcasses (Mazur-Panasiuk & Woiniakowski, 2020) and that wild boar (Probst et al., 2017) and wild pigs (Turner et al., 2017) make contact with their dead conspecifics in late stages of carcass decay. Carcass-based transmission essentially extends the infectious period after an individual dies from infection, which can drive up incidence and spatial spread. Thus, ASFv transmission models are very sensitive to carcass-based transmission parameters (Lange, 2015; Lange & Thulke, 2017; Pepin et al., 2020, 2021). Because we did not have data from the United States to inform this parameter, we assumed that carcass contact rates would be similar to the frequency with which wild pigs visit bait sites or food supplements and that persistence of ASFv in carcasses reflects data from Eastern Europe (we chose 4.3 weeks; an average for the longer times during the cold months and shorter times during the warm months). However, in the Southern United States, temperatures are warmer on average than in Eastern Europe, and scavenger populations are also abundant. In these regions, pig carcasses have been observed to have complete removal of flesh from carcasses within 24 h in some cases (Turner et al., 2017), which may decrease the likelihood that other wild pigs visit the carcass. Estimates of contact rates with carcasses in ecological conditions in the United States will be important for reducing uncertainty in estimates of spatial spread and optimal control area size for a response to the ASFv in the United States.
We assumed density-dependent reproduction and capture success. While there is anecdotal evidence that reproduction rates and capture success are affected by population density, there are few data to inform the relationships, especially for the United States (N. S. Snow et al., 2020). Density-dependent reproduction would drive up the birth rates as the population is reduced during a response, which would also increase the immigration pressure from outside the response area. For responses that last 6 months or longer, inputs from births and immigration could substantially impact disease spread and persistence and increase the time to elimination. Thus, a better understanding of demographic responses to intense control is likely important for planning effective mitigation. Relatedly, capture success is known to decrease as population density decreases (Choquenot et al., 1999) because it becomes more difficult to find individuals using the same amount of effort. However, this relationship likely varies based on removal techniques, habitat and weather and has not been formally resolved for any of these conditions in the United States. More empirical data about the relationship between density and capture success in different ecological settings would help to refine predictions of elimination time using different culling capacities across ecoregions in the United States.
Finally, in this work, we assumed epidemiological characteristics similar to the virulent genotype II that has been circulating in wild boar in Eastern Europe (i.e., 95% mortality rate with mean incubation and infectious periods of 4 and 5 days, respectively). However, data from an unpublished virulence study using an isolate from the recent introduction in Dominican Republic suggest that this ASF strain may be less virulent than the traditional Georgia 2007 strain. These less virulent genotypes have also been observed in other settings (Gallardo et al., 2018) and could cause different dynamics of spatial spread relative to the more virulent strains (Gallardo et al., 2015). Thus, an important future direction is to examine how genotypes with different epidemiological characteristics might affect the optimal response areas. This question can be answered with the framework we have developed. Experiments with less virulent strains that measure epidemiological parameters such as incubation and infectious periods, the frequency that infected individuals recover, the length and strength of immunity in recovered individuals and the effects of these strains on detection (through clinical signs or pre-existing assays) will be important for predicting optimal surveillance and response plans across a variety of strains.
5 CONCLUSION
Our framework provides a platform for determining optimal response areas for a variety of different ecological and management conditions using an adaptive response area around detections. By examining a wide range of detection times, culling capacities and ecological conditions, we identified that optimal response areas are affected by all these features, especially local ecology. For most conditions, large control radii around detections (usually 14 km—near the maximum we examined) were needed to reach elimination as rapidly as possible with the least amount of spatial spread. It was always best to focus on culling nearest to detections and work in-to-out, as most wild pigs are eliminated, rather than starting at the outer edges of the response area and working out-to-in. Culling capacities ≥ 15% of the population weekly or early detection times (8 weeks or less) allowed for smaller control radii. Wild pig movement profiles and contact rates were more important in determining the optimal response area than early outbreak incidence (a similar metric to R0), highlighting the importance of understanding movement and contact in wild pigs in different ecological settings and refining response plans based on the local movement ecology of wild pigs.
ACKNOWLEDGEMENTS
The research was funded by the National Feral Swine Damage Management Program of the United States Department of Agriculture, Animal and Plant Health Inspection Service. The contributions of JCB were partially supported by the US Department of Energy under Award No. DE-EM0005228 to the University of Georgia Research Foundation. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer or otherwise does not constitute or imply its endorsement, recommendation or favouring by the US Government or any agency thereof. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the US Government or any agency thereof.
ETHICS STATEMENT
The authors confirm that the ethical policies of the journal, as noted on the journal's author guidelines page, have been adhered to. No ethical approval was needed, as this is a simulation modelling article. Field data of animal movement were taken from previously published work.
CONFLICT OF INTEREST
The authors declare no conflicts of interest.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




