Volume 47, Issue 12 pp. 5076-5088

ORIGINAL ARTICLE

Open Access

Analysis of root-environment interactions reveals mechanical advantages of growth-driven penetration of roots

Yoni Koren,

Yoni Koren

School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

Search for more papers by this author

Alessia Perilli,

Alessia Perilli

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel

Search for more papers by this author

Oren Tchaicheeyan,

Oren Tchaicheeyan

School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

Search for more papers by this author

Ayelet Lesman,

Corresponding Author

Ayelet Lesman

[email protected]

School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

Correspondence Ayelet Lesman, School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Yasmine Meroz, School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Search for more papers by this author

Yasmine Meroz,

Corresponding Author

Yasmine Meroz

[email protected]

orcid.org/0000-0003-4752-0372

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel

Correspondence Ayelet Lesman, School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Yasmine Meroz, School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Search for more papers by this author

Yoni Koren,

Yoni Koren

School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

Search for more papers by this author

Alessia Perilli,

Alessia Perilli

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel

Search for more papers by this author

Oren Tchaicheeyan,

Oren Tchaicheeyan

School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

Search for more papers by this author

Ayelet Lesman,

Corresponding Author

Ayelet Lesman

[email protected]

School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

Correspondence Ayelet Lesman, School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Yasmine Meroz, School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Search for more papers by this author

Yasmine Meroz,

Corresponding Author

Yasmine Meroz

[email protected]

orcid.org/0000-0003-4752-0372

Center for Physics and Chemistry of Living Systems, Tel Aviv University, Tel Aviv, Israel

School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel

Correspondence Ayelet Lesman, School of Mechanical Engineering, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Yasmine Meroz, School of Plant Science and Food Security, Tel Aviv University, Tel Aviv, Israel.

Email: [email protected]

Search for more papers by this author

First published: 14 August 2024

https://doi.org/10.1111/pce.15089

Citations: 1

Yoni Koren and Alessia Perilli contributed equally to this work.

Share a link

Email
Wechat
Bluesky

Abstract

Plant roots are considered highly efficient soil explorers. As opposed to the push-driven penetration strategy commonly used by many digging organisms, roots penetrate by growing, adding new cells at the tip, and elongating over a well-defined growth zone. However, a comprehensive understanding of the mechanical aspects associated with root penetration is currently lacking. We perform penetration experiments following Arabidopsis thaliana roots growing into an agar gel environment, and a needle of similar dimensions pushed into the same agar. We measure and compare the environmental deformations in both cases by following the displacement of fluorescent beads embedded within the gel, combining confocal microscopy and Digital Volume Correlation (DVC) analysis. We find that deformations are generally smaller for growing roots. To better understand the mechanical differences between the two penetration strategies, we develop a computational model informed by experiments. Simulations show that, compared to push-driven penetration, grow-driven penetration reduces frictional forces and mechanical work, with lower propagation of displacements in the surrounding medium. These findings shed light on the complex interaction of plant roots with their environment, providing a quantitative understanding based on a comparative approach.

1 INTRODUCTION

Plant roots have the extraordinary ability to sense the environment and adaptively grow inside their medium (Darwin and Darwin, 1880), making them one of the most efficient soil explorers amongst living organisms. This is critical for plant survival, enabling water and nutrient uptake, as well as anchoring (Dupuy et al., 2005; Gliński and Lipiec, 2018; Stubbs et al., 2019; Taiz et al., 2014). As opposed to the pushing penetration strategy commonly used by many digging organisms, roots penetrate by growing. This unique growth-driven mechanism has recently inspired the development of a new generation of growing robots (Hawkes et al., 2017; Meder et al., 2023; Sadeghi et al., 2017; Wooten and Walker, 2018).

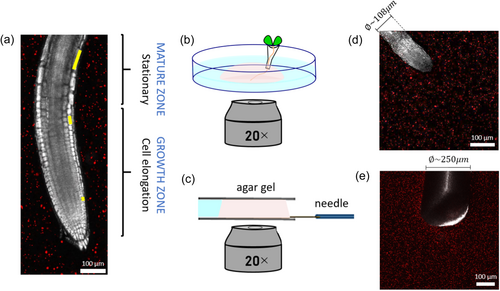
Root growth generally entails new cells being produced at the tip, just behind the root cap, and an increase in internal turgor pressure, overcoming external resistance, driving their elongation within a fixed sub-apical region called the growth zone (Taiz et al., 2014). The cells in the growth zone reach a maximal size, and become part of the mature zone, which remains fixed over time, as shown in Figure 1a. While it is generally accepted that growing roots excel at soil penetration, the underlying mechanism is not well understood. The measured pressure exerted by growing root tips, in the range of 0.1–1 MPa (Clark et al., 2003; Kolb et al., 2017; Misra et al., 1986), is generally lower than the resistance of soil to penetration, in the range of 0.5–4.5 MPa in soft soils (Ani et al., 2011; Herrick and Jones, 2002; Topakci et al., 2010). Traditionally this difference has been attributed to the production of mucilage at the tip of the root, which decreases friction (Bengough et al., 2006; Kirby and Bengough, 2002; Kolb et al., 2017; Ruiz et al., 2016; Tonazzini et al., 2013; Vollsnes et al., 2010). However, recent observations indicate that soil displacements are highest in the immediate vicinity of the root tip, falling at some distance behind it (Bull et al., 2020; Keyes et al., 2016, 2017; Vollsnes et al., 2010), suggesting a relation to the extent of the growth zone. This has motivated work comparing penetration driven by growing versus pushing (Sadeghi et al., 2013, 2014; Tonazzini et al., 2013). For example, Sadeghi et al. developed a self-growing robot that moves by 3D printing new material at the tip, and demonstrated that the addition of material (growth) facilitated soil penetration, since the rest of the robot (representing the mature zone) is stationary, thus decreasing peripheral friction and energy consumption down to 70% compared to pushing (Sadeghi et al., 2014). However, there are currently no experimental studies directly comparing the mechanical implications of penetration driven by growth (roots) with penetration driven by pushing.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Experimental setup of a growing root and a pushed needle penetrating agar gel. (a) Confocal image of a growing root with its distinct zones: cells elongate within the growth zone, and finally reaching their final size in the static mature zone. Three single cells are marked in yellow at different stages, demonstrating elongation as they get further away from the tip. (b) Schematics showing the glass dish with the Arabidopsis root growing into the agar gel droplet submerged in water and imaged from the bottom using a confocal microscope. (c) Schematics of the needle experiment where the needle is moving horizontally in the agar gel between two coverslips, submerged in water and imaged from the bottom using a confocal microscope. (d, e) Confocal image showing the root tip (d) and needle tip (e) surrounded by agar embedded with fluorescence reporter beads.

While such experimental observations could provide essential insight, the complexity of plant root experiments limits the identification and control of the different contributions, such as friction and changes in mechanical properties of the medium, as well as the role of turgor pressure and cell wall acidification. This motivates the use of experimentally informed computational models, which allow precise control over the problem through the systematic and independent change of relevant parameters. Furthermore, while some aspects of root mechanics and their impact on growth have been elucidated (Goriely, 2017; Jin et al., 2020; Kolb et al., 2017; Lockhart, 1965; Silverberg et al., 2012; Thompson and Holbrook, 2004; Trinh et al., 2021), and recent theoretical models have described the mechanical interaction of a growing root with an obstacle or its own weight (Chelakkot and Mahadevan, 2017; Porat et al., 2023; Sipos and Várkonyi, 2022), a comprehensive understanding of the mechanical aspects involved in soil penetration of growing roots is still lacking. In particular, computational examination of object penetration have predominantly concentrated on pushing mechanisms that do not consider growth (Assaad et al., 2015; Calusi et al., 2020; Jushiddi et al., 2019; Kataoka et al., 2008; Kirby and Bengough, 2002; Liyanapathirana, 2009; Oldfield et al., 2013; Ruiz et al., 2016; Tolooiyan and Gavin, 2011; Wei et al., 2005), and existing models considering root growth provide limited analyses of the mechanical interaction with the surrounding medium (Bastien et al., 2014; Bidhendi and Geitmann, 2018; Fayant et al., 2010; Porat et al., 2020, 2024; Seidel et al., 2022; Tomobe et al., 2023; Yanagisawa et al., 2015).

In this work, we present an experimental and computational study comparing growth- and push-driven penetration mechanisms, in terms of mechanical interactions with the surrounding medium. We measure the medium deformation imposed by Arabidopsis thaliana roots growing in an agar gel, compared to a pushed micro-needle of similar dimensions, and develop a 3D Finite Elements (FE) numerical model informed by experimental measurements. Based on simulations, we perform a quantitative analysis of these scenarios showing that growing is an energetically favorable penetration mechanism over pushing, leading to smaller deformations in the embedding medium.

2 MATERIALS AND METHODS

2.1 Root experiments

Arabidopsis roots were grown in agar hydrogel, and their growing process was recorded in real-time by confocal microscopy. The experimental stages included germination, initial growth, transfer for microscopy observation, and finally tracking the displacements of fluorescent beads embedded in the gel as the root grew further in the gel.

2.1.1 Seed germination

The medium for seed germination was prepared using 0.6% (w/v) Phytagel (Sigma P8169), Murashige and Skoog (MS) salts with vitamins (1.15 gl⁻¹) (M0222, Duchefa, 2003 RV Haarlem, Netherlands), MES monohydrate (0.5 gl⁻¹) (M1503, Duchefa, 2003 RV Haarlem, Netherlands) and D-(+)-Sucrose (10 gl⁻¹) (Bio-Lab Ltd). Sterile 90 mm Petri dishes were filled to a height of approximately 0.8 cm with this medium. 0.5–10 µL pipette tips (Gilson Clear Micro P10) were filled with the gel in liquid form, using a micropipette, with approximately 5 µL of medium from the Petri dish. Once the medium in the tips had solidified, they were cut at a distance of approximately 0.5 cm from the end and placed upright into the Petri dishes containing solid growth medium; a total of eight to twelve cones were placed in every Petri dish. On top of each of the cones, an Arabidopsis thaliana seed was placed with the help of a sterile wooden toothpick (Supporting Information S1: Figure S1). The dish was then sealed and put in a growth chamber to start germination; the growth conditions were 21°C at a 16 h light/8 h dark cycle. After 4–7 days, shoots grew upwards and roots grew down the cone towards the aperture.

2.1.2 Preparation of the set-up for microscope imaging

When the roots had grown about 1 cm past the cone aperture (between 7 to 10 days), they were selected for microscope imaging. The roots' growth was imaged in a second medium, made of 0.6% (w/v) agar gel (Agarose, low gelling temperature; Sigma A9045) supplemented with the same components mentioned in the previously described growth medium. The melted gel was mixed with fluorescent microbeads (FluoSpheres^TM Carboxylate-Modified Microspheres, 1.0 µm, orange fluorescent (540/560), 2% solids; Fischer F8820) in 0.75% concentration (v/v). To homogeneously distribute the beads, the mixture was agitated using a vortex mixer for about 1 min. The cone containing one of the selected roots was lifted from the growth medium using forceps and placed on a glass bottom dish (dish size 35 mm, well size 14 mm, #1.5 cover glass), with the root lying on the glass and the cone held upright using a piece of PDMS. The gel-bead mixture, still liquid but not too hot so as not to damage the root, was then slowly pipetted on top of the root, forming a hemispherical shaped droplet. Once the gel solidified, the glass bottom dish was filled with water to avoid dehydration during the imaging process. The glass bottom dish was placed in the growth chamber for a few hours to allow the plant to adapt to the new environment.

2.2 Needle pushing experiment

The experimental setup for the needle experiment consisted of a needle insertion device (SENSAPEX micromanipulator), the same agar gel that was used for the Arabidopsis thaliana root imaging, and the Zeiss confocal microscope (Zeiss 880, 20X magnification lens). The micromanipulator was placed upon the microscope stage (Supporting Information S1: Figure S2), holding and actuating a shaft that contained a stiff tungsten needle of 250 µm diameter and length of 1 cm, oriented horizontally and located about 100 µm above a glass coverslip (#1.5, 24 × 60 mm) over the microscope objectives. A 2.5 mm-thick strip of silicone rubber was glued to the coverslip in advance, serving as a mold for the agar gel. The vertical distance between the needle and the coverslip was within the working distance of the objective ( ~ 0.55 mm). When the correct position of the needle tip was detected in the microscope, a 1 mL agar gel embedded with micro-fluorescence beads (with the same concentration and composition as described in Section 2.1.2) was micropipetted and let solidify on the glass coverslip, covering the horizontal needle and surrounded by the silicone strip. This was made to ensure that the front part of the needle was embedded in the gel before the start of the experiment. After the gel was fully solidified, a second coverslip was placed on top of the gel, holding it gently to prevent any boundary motions of the gel during the needle insertion. Thus, the gel was 2.5 mm-thick before imaging. The silicone mold also contained a water reservoir keeping the gel moisturized, and preventing it from drying. A few drops of water were then carefully added around the gel through a small gap between the upper coverslip and the silicone strip, and the system was then left for stabilization for another 20 min. The needle was gradually inserted into the agar gel using the micromanipulator. The micromanipulator does not allow continuous penetration, and instead, we appproximated the root growth rate by inserting steps of 2.5 µm, at an insertion speed of 100 µm/s (the minimal possible speed for the device). Each step was followed by a 30 min break to allow the gel to stabilize.

2.3 Confocal imaging and agar displacement measurement

For both the needle and the root experiments, the imaging process was performed with an 880 Zeiss confocal microscope using a 20X magnification lens. The 3D root images were captured with an image resolution of 512 × 512 × 100 pixels, with 1.38 µm/pixel, for a total area of 708.49 × 708.49 µm² on the xy plane and z-stack of 138 µm. For the root, a time lapse was generated taking Z-stack images at intervals of 4 min for several hours.

Root growth deformed the embedding gel, and displacements were quantified by tracking fluorescent beads embedded in the gel using a Digital Volume Correlation (DVC) algorithm (Franck et al., 2007, 2011; Lesman et al., 2014). Due to instabilities of bead movements at the root-gel interface, displacements around the root were calculated from a minimal distance from the tip (equivalent to 0.6 of the root thickness). The 3D volumetric image was divided into subsets, which were then cross-correlated to compute the 3D displacement field of each subset. In our case, the size of the subset was ~44 × 44 × 44 µm³ and the spatial resolution was 22 µm. We measured the typical experimental noise in the system by quantifying the systematic error resulting from imaging artifacts or thermal fluctuations, performing DVC on the same agar gel with no roots/needle imaged over time. We found mean values generally around zero, indicating no global drifts, with fluctuations within 0.3 µm and 0.9% for the displacement and strain measurements, respectively (Supporting Information S1: Figure S3). These values set the noise threshold for measuring displacements and strains in our system.

For the needle experiments, the 3D confocal image stack was taken after a tip displacement of 2.5 µm, and the DVC analysis was performed taking the previous image as a reference. During the 30 min break needed for stabilization period, a z-interval of approximately 300 µm was recorded using the confocal microscope. The image resolution was 700 × 700 pixels, with 1.0 µm/pixel for a total area of 708.49 × 708.49 µm². To perform similar analyses in the case of the root and needle, we manually tracked the position of the root tip in all time-frames, identifying time points at which the root tip made a 2.5 µm displacement. Let k be the number of time frames corresponding to such 2.5 μm intervals, each i-th image was used as a reference for the (i + k)-th image in the DVC analysis (for instance, in one case the root penetrated 2.5 µm every 4 timeframes, so the first image was correlated to the 5th, the 2nd to the 6th, the 3rd to the 7th and so on). In this way, for each experiment made of N images, we obtained a series of (N-k) DVC analyses corresponding to the same displacement of 2.5 µm and statistically equivalent to each other. In the case of the needle experiments, four DVC analyses were performed for each experiment (one for each time step).

2.4 Agar gel characterization

A cylindrical sample of the same agar gel used for the root and needle experiments was prepared using a hollow cylindrical 3D-printed mold made of poly(lactic acid) (PLA) with an external diameter of 40 mm, internal diameter of 14.2 mm and height of 11.4 mm, that we designed using the software SOLIDWORKS (SolidWorks) and printed with a commercial Fused Deposition Modeling (FDM) 3D printer (Stratasys Fortus 450, ASA filament) for the purpose of the mechanical characterization of the gel. A thin layer of grease was applied to the inner surfaces of the 3D printed mold to prevent friction. The mold was placed on the bottom surface of a DHR-3 rheometer (Discovery Hybrid Rheometer, TA Instruments; 50 N force transducer, normal force resolution 0.5 mN, normal force sensitivity 0.005 N), between the two loading plates (Supporting Information S1: Figure S4a,b) and 1.8 mL of gel was poured into the mold and immediately sealed with a thin circular glass coverslip, to make sure that the upper surface of the gel is straight and parallel to the compressing plate. The mold consisted of two parts, so that they could be disassembled after gel polymerization. After 1 h of polymerization at room temperature, the mold was carefully removed and the gel was surrounded by a ring-shaped silicone strip, to create a border for a water reservoir keeping the gel moisturized. Rheometer measurements were performed at room temperature and by enclosing the rheometer stage with a polythene sheet to prevent dehydration. The upper and moveable plate (20 mm diameter) was lowered until it touched the top surface of the gel evident by non-zero normal forces. The normal force was set to zero before starting to compress the gel. Compression tests were performed with a constant speed of 0.055 µm/s, targeting the slow growth movement of roots. This was made by imposing a uniform downward motion of the upper plate, and the normal force was monitored over time. Measurements were repeated three times using the rheometer.

The raw data contained the gap distance between the two plates and the normal force. Subsequently, this data was used to calculate the engineering axial strain (ε) and engineering axial stress (σ) of the gel, which are given by:

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0001" display="block" wiley:location="equation/pce15089-math-0001.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><mi>\unicode{x003B5}</mi><mo>\unicode{x0003D}</mo><mfrac><mrow><mo>\unicode{x02206}</mo><mi>l</mi></mrow><msub><mi>l</mi><mn>0</mn></msub></mfrac></mrow></mrow></math>

(1)

where

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0002" wiley:location="equation/pce15089-math-0002.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><mo>\unicode{x02206}</mo><mi>l</mi></mrow></mrow></math>

is equal to the initial height of the sample

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0003" wiley:location="equation/pce15089-math-0003.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><msub><mi>l</mi><mn>0</mn></msub></mrow></mrow></math>

minus the gap distance, and

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0004" display="block" wiley:location="equation/pce15089-math-0004.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><mi>\unicode{x003C3}</mi><mo>\unicode{x0003D}</mo><mfrac><mi>F</mi><msub><mi>A</mi><mn>0</mn></msub></mfrac></mrow></mrow></math>

(2)

where

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0005" wiley:location="equation/pce15089-math-0005.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><mi>F</mi></mrow></mrow></math>

is the normal force, and A₀ is the initial cross-sectional area of the gel sample, that is equal to πd₀²/4 (d₀ is the original diameter of the sample). We assumed that the cross-sectional area of the sample did not considerably change throughout the test due to the relatively small change in gap distance. The test data were averaged to extract the resulting stress-strain relation curve (using Equations 1 and 2), to be used in the FE model. The stress–strain curve σ(ε) displays a linear elastic region followed by a nonlinear response above a critical compressive strain, to obtain an ‘elastic-plastic’ behavior of the simulated agar gel (Supporting Information S1: Figure S4c). That behavior is consistent with a recent study that reported a similar mechanical response of low concentration agar gel under a slow compression ramp (Ed-daoui and Snabre, 2021). The elastic regime of the curve was linearly fitted to obtain a Young's Modulus of 2361 Pa, a typical value for low-concentrated agar of 0.6% (Delaine-Smith et al., 2016; Hobson et al., 2021). The onset of the plastic regime, which is characterized by approximately constant stress, occurred at ε ≈ 2%–4% strain.

To study the effect of compression speed on the normal forces applied on the gel, stress relaxation experiments were performed on a weakly compressed cylindrical agar sample (ε = 5%) of the same dimensions and method as described above. First, the sample was compressed at some constant speed (ranged between 10 and 100 µm/s). The sample was then kept at the same strain for half an hour without applying a load, during which the force was monitored every 5 s.

2.5 Finite element modeling

For the FE analysis, the ABAQUS Standard/Implicit FE solver (SIMULIA, 2014) in its nonlinear analysis mode was used to simulate the push- and growth-driven penetration of a thin cylindrical and rigid object into a domain, with material properties of the agar gel measured in 2.4. Root parametrization, FE model construction and further details of the simulation setup are detailed in the following sections. To achieve a proper comparison of the push- and growth-driven penetrations, the tip of the penetrating object in both cases (second FE model; see Section 2.5.3 for details) was given the same total displacement of 0.52 mm, so that in each increment the tip penetrates the same distance. This way, each of the 100 time points are comparable.

2.5.1 Root growth parametrization

The model of root geometry was designed based on an experimental image of Arabidopsis Thaliana root taken with the confocal microscope. The shape of the root was approximated by a cylinder connected to an elliptical dome, providing a simplified 3D geometry with similar shape and dimensions as the root (Figure 4a). We assume a vertically positioned root throughout simulations, and disregard gravity effects. To simplify the model system and avoid failure of the material due to extreme deformations, we introduce a burrow within the gel domain, with a diameter corresponding to 0.9 the root diameter; as the root moves in the burrow, it is always in contact and pushes against the burrow wall, leading to friction. To compare the two penetration mechanisms (growing vs. pushing) and to account for differences between them, we ensured that the burrow is long enough to allow for sufficient penetration length. Growth occurs only in the growth zone, defined within a fixed region from the tip of length L_gz. We assume an exponential growth process (Bastien et al., 2014), with a uniform growth rate ε₀ (with dimensions 1/s) within the growth zone. For an infinitesimal segment of length Δ at distance s from the tip, the elongation reads:

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0006" display="block" wiley:location="equation/pce15089-math-0006.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><mfrac><mrow><mo>\unicode{x02202}</mo><mi mathvariant="normal">\unicode{x00394}</mi><mrow><mo stretchy="false">(</mo><mrow><mi>s</mi><mo>,</mo><mi>t</mi></mrow><mo stretchy="false">)</mo></mrow></mrow><mrow><mo>\unicode{x02202}</mo><mi>t</mi></mrow></mfrac><mo>\unicode{x0003D}</mo><mi>\unicode{x003B5}</mi><mrow><mo stretchy="false">(</mo><mi>s</mi><mo stretchy="false">)</mo></mrow><mi mathvariant="normal">\unicode{x00394}</mi><mrow><mo stretchy="false">(</mo><mrow><mi>s</mi><mo>,</mo><mi>t</mi></mrow><mo stretchy="false">)</mo></mrow></mrow></mrow></math>

(3)

where

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0007" display="block" wiley:location="equation/pce15089-math-0007.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><mi>\unicode{x003B5}</mi><mrow><mo stretchy="false">(</mo><mi>s</mi><mo stretchy="false">)</mo></mrow><mo>\unicode{x0003D}</mo><mfenced close="" open="{"><mtable columnalign="left" displaystyle="true"><mtr><mtd><msub><mi>\unicode{x003B5}</mi><mn>0</mn></msub><mi mathvariant="italic">if</mi><mspace width="0.25em"/><mi>s</mi><mo>\unicode{x0003C}</mo><msub><mi>L</mi><mi mathvariant="italic">gz</mi></msub></mtd></mtr><mtr><mtd><mn>0</mn><mspace width="1.20em"/><mi mathvariant="italic">otherwise</mi></mtd></mtr></mtable></mfenced></mrow></mrow></math>

(4)

In other words, the elongation of the growth zone has the form of exponential growth, where with each time increment dt, Δ is lengthened by ε₀Δdt (Schnepf et al., 2018). The root body is discretized into vertical sections (i.e., elements), which are connected by characteristic key points (generally located at their corners; i.e., nodes). Numerically, at every step n the length of an element inside the growth zone is updated as follows:

<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0008" display="block" wiley:location="equation/pce15089-math-0008.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><msub><mi mathvariant="normal">\unicode{x00394}</mi><mi>n</mi></msub><mo>\unicode{x0003D}</mo><msub><mi mathvariant="normal">\unicode{x00394}</mi><mrow><mi>n</mi><mo>\unicode{x02212}</mo><mn>1</mn></mrow></msub><mrow><mo stretchy="false">(</mo><mrow><mn>1</mn><mo>\unicode{x0002B}</mo><mi>\unicode{x003B5} dt</mi></mrow><mo stretchy="false">)</mo></mrow></mrow></mrow></math>

(5)

where dt is a discretization of time. This procedure determines the evolution of the vertical coordinate (y) of every element. The cross-section coordinates (x and z) remain unvaried in the cylindrical part of the root, while the convex region (the root tip) is translated as a rigid body (Figure 4b; see an animated demonstration of the growth in Supporting Information S1: Video S1, where for simplicity only the border line of the modeled root is shown). To reduce the computational cost of simulations, we chose a growth zone of L_gz = 0.1 mm, smaller than the observed values for Arabidopsis ~1 mm (Beemster and Baskin, 1998), without loss of generality. We started with a very dense discretization of the growth zone, to maintain a significant number of elements inside the growth zone at all times without the need of adding new elements, since elements progressively grow out of the elongation zone and become stationary. To avoid high stresses in the elements in the growth zone due to the elongation, ‘surface elements’ were used (SIMULIA, 2014). These elements can support any translation of their nodes without developing stresses, since they have no inherent stiffness. The root geometry was discretized using linear 4-node quadrilateral surface elements, and no material properties were allocated since these elements are computationally considered rigid compared to the gel.

2.5.2 Model parameters

The material properties of the medium are set based on the rheological measurements detailed in 2.4, with a Young's Modulus of 2361 Pa, and the Poisson ratio of 0.49 (Jushiddi et al., 2019; Nayar et al., 2012). The plastic region was defined in correspondence to the plateau in the stress-strain curve obtained from the rheological measurements, starting at 5% strain, and the corresponding yield stresses were calculated with the calibration tool in ABAQUS/CAE to match the experimental stress-strain curve (Supporting Information S1: Figure S4c). The agar gel was meshed with 8-node linear brick elements, reduced integration and hourglass control, to facilitate the simulation convergence (SIMULIA, 2014). A surface-to-surface contact interaction was defined in the interface between the gel domain and the root's outer surface, with different values of friction coefficients, to analyze the effect of friction. A static, general step was used to run the simulations, divided into 100 increments, which are referred to as frames, or ‘time points.’ Using a static step is reasonable, as the slow processes of root growth and needle insertion can be considered as quasi-static, with the system in equilibrium along the duration of penetration.

2.5.3 Simulations setup and boundary conditions

Two different models were developed. (1) The first model was designed to validate the mechanical response of the computational model by comparing the push-driven simulations and the needle experiment. The penetrating object was initially placed within the modeled agar gel, similar to the starting point in the needle experiment where the gel polymerized around the needle. The diameter and shape of the tip were determined to resemble the actual needle. As for the boundary conditions, the bottom gel surface was constrained in the vertical (y) direction, while the side surfaces were constrained in the lateral (x and z) directions. The penetrating object was constrained in both lateral directions, and was forced to translate 10 µm vertically downwards, similar to the total displacement of the needle (Figure 3a). We also performed a mesh sensitivity study of the model (see Supporting Information S1: Figure S5), finding that further reduction of mesh size did not substantially change the results of FE simulations. However, a finer mesh does significantly increase computational time. (2) The second FE model was developed to study the differences between push- and growth-driven penetrations. Root growth was simulated with distinct zones of elongation and maturation, where the maturation part is stationary and the growth zone elongates to resemble root growth, as detailed in Section 2.5.1. Push-driven simulations had the same body geometry but involved rigid-body motion. In both type of simulations, we included a burrow into which the body penetrates, which is 10% more narrow than the body diameter to allow access ahead of the body while pushing on the sides during penetration. Similar boundary conditions as in the first model were applied to the agar domain (Figure 4c).

3 RESULTS

3.1 Quantitative characterization of penetration experiments: Growing root versus pushed needle

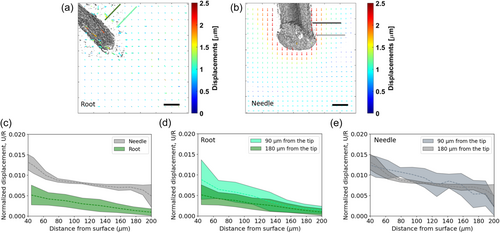
We performed an experimental characterization of the penetration of Arabidopsis thaliana roots growing in an agar gel, and a micro-needle pushed into the same medium (illustrated in Figure 1b,c). We placed an Arabidopsis root in an agar gel sample and recorded its growth using confocal microscopy at intervals of 4 min during several hours, with an average penetration rate of 10 μm per hour. Similarly, a needle with comparable dimensions was inserted in the same type of gel, performing four consecutive displacements of 2.5 μm each, leading to a total penetration of 10 μm (see Methods). Supporting Information S1: Figure S6 presents rheometer results, confirming that the waiting time between each needle displacement (30 min) was sufficient for relaxation (>15 min), and that slow and fast loading rates relax to similar values. This suggests that the varying penetration rates between the root and the needle are unlikely to significantly impact gel displacements. To resolve the 3D displacement field of the gel due to penetration, we track the displacement of fluorescent beads embedded within the gel (red speckles in Figure 1a,d,e) using a Digital Volume Correlation (DVC) analysis (see Methods). Quiver plots computed by the DVC algorithm for both the root and the needle are shown in Figure 2a,b, respectively, and in Supporting Information S1: Figure S7. Color maps of the effective gel strains are shown in Supporting Information S1: Figure S8 with strains ranging 1%–1.5% for the root and 1%–3% for the needle. Assuming radial symmetry, we consider a planar projection of displacements larger than the noise level of the system (~0.2 μm, see Supporting Information S1: Figure S3). In both cases, the displacements, mainly detected close to the surface of the root or the needle, were generally oriented in the direction of penetration. We plotted the radial displacements for two distances from the tip (90and 180 µm; lines of green shades in Figure 2a and lines of gray shades in Figure 2b). To account for differences in dimensions between the root and needle (the root and needle average diameters are approximately 108 and 250 µm, respectively, see Figure 1d,e), we normalized the radial displacements by the root/needle radius (Ganju et al., 2020; Peinke et al., 2020). We verified that normalizing to the radius is appropriate in our system using a computational analysis (Supporting Information S1: Figure S9, Section 2.5 in the Methods), demonstrating that the impact of diameter differences can be effectively removed through normalization to the radius. Displacements are higher for needle penetration (Figure 2c), suggesting a greater impact on the surrounding medium. Comparing the radial displacements at 90 and 180 µm from the tip (Figure 2d,e), we find that while these are similar for the needle, for the growing root displacements are higher closer to the tip. This difference likely stems from the root elongating (growing) closer to the tip, whilst farther away is the mature zone, which remains stationary relative to the medium. The difference in tip geometries between needle and root is expected to have a minor impact on the radial displacements, as shown by a computational analysis in Supporting Information S1: Figure S10.

3.2 Finite element (FE) computational model for agar gel penetration

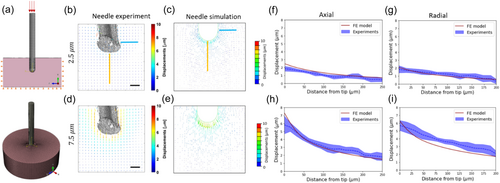
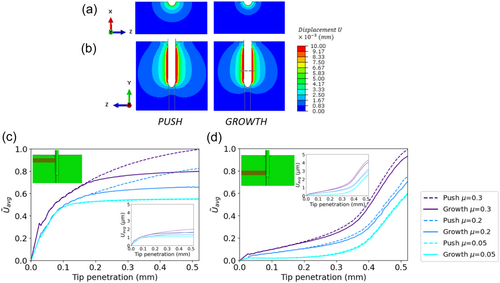
To obtain a quantitative understanding of the displacement fields observed in the pushing (needle) and growing (root) experiments, we developed a FE model describing these scenarios (Figure 3a; see Methods). To validate that our model captures the mechanical response of the agar gel, we compared the measured DVC displacements of the needle experiment with a simulated needle penetration, as shown in Figure 3b–e for tip penetrations of 2.5 and 7.5 µm. In these simulations, we implemented the mechanical properties of agar gel in compression, as measured by a rheometer (see Section 2.4 in Methods for further details) and assumed a contact friction coefficient of μ = 0.05. We find that the experimental and computational displacement profiles agree along both the axial and radial (90 µm from the tip) paths, for both 2.5 µm penetration (Figures 3f,g) and 7.5 µm penetration (Figure 3h,i), confirming the model reliably represents the behavior and characteristics of the agar gel in these experiments.

3.3 Growth reduces frictional forces and mechanical work

Building on our validated numerical framework, we now aim to computationally elucidate the differences between push-driven and growth-driven penetration. We use an identical shape in both types of simulations, informed by Arabidopsis thaliana root geometry (Figure 4a). The simulation of root growth is based on experimental observations of Arabidopsis roots (Porat et al., 2024) (see Section 2.5.1 in Methods for further details). Figure 4b shows snapshots of a simulated growing root, where the elongating growth zone is kept at a fixed length L_gz = 0.1 mm (smaller than the observed value L_gz ~ 1 mm to reduce computational resources, without loss of generality—see Methods), and the mature zone increases with time (see Supporting Information S1: Video S1). The boundary between the growth and mature zones is marked with a blue line. To capture differences between push-driven and growth-driven penetration, we focus on differences in radial effects that may emerge due to the growth-driven elongation and maturation zones, as motivated by the experimental observations in Figure 2. To avoid failure of the material in extreme deformations, we simplify our model by introducing a burrow within the gel domain with a diameter 0.9 of the root diameter (Figure 4c). As the root moves in the burrow, it pushes against it, leading to friction and radial deformations. We ran simulations for both pushing and growing penetration mechanisms using identical configurations, enabling us to quantitatively study key differences.

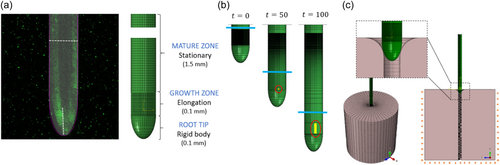
Figure 5a compares the contact shear force, F_s, developed at the interface of the root body and the agar for both push and growth simulations following a tip displacement of 0.52 mm, with friction μ = 0.2. The evolution of forces over time can be seen in Supporting Information S1: Video S2. While the contact shear force is approximately constant along the pushed body, the growing root is characterized by a sharp decrease in forces farther away from the growing tip, where the mature zone stops moving relative to the agar gel (marked by a blue line). These findings hold for other values of μ in the range of 0.05–0.3 (see Supporting Information S1: Figure S11). To follow the evolution of differences in contact forces with time, that is with increasing tip displacement, we define the total frictional force (parallel to the direction of penetration) during penetration by summing all the forces acting on the body surface: $<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0009" wiley:location="equation/pce15089-math-0009.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><msubsup><mi>F</mi><mi>S</mi><mi mathvariant="italic">tot</mi></msubsup><mo>(</mo><mi>t</mi><mo>)</mo><mo>\unicode{x0003D}</mo><msub><mo>\unicode{x02211}</mo><mi>i</mi></msub><mrow><msub><mi>F</mi><mrow><mi>s</mi><mo>,</mo><mi>i</mi></mrow></msub><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mrow></mrow></math>$ , where i denotes the number of a node located on the body surface. The evolution of total frictional force is shown in Figure 5b. As expected, in the beginning of penetration the force increases with time in an approximately identical manner for both push and growth simulations, as the front part of the body was pushed similarly in both mechanisms. Once the tip penetrates beyond 0.2 mm into the burrow, the static mature zone begins to form, revealing the emerging distinctions in penetration mechanisms. At this point, pushing exhibits higher total frictional force compared to the growing counterpart, for any friction coefficient.

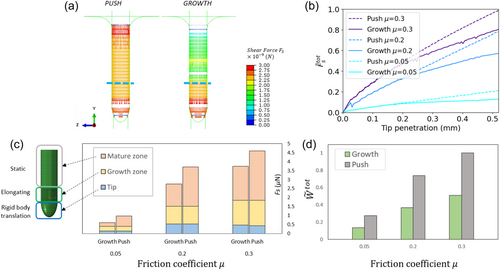
Next, to better understand the differences in frictional forces between growing and pushing penetration, we compare the local contact shear forces within different regions along the body—the mature zone, the growth zone, and the tip (Figure 5c). In the pushing simulation no elongation occurs, and the regions refer to the equivalent positions along the organ. Namely, we measure $<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0012" wiley:location="equation/pce15089-math-0012.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><msub><mi>F</mi><mi>S</mi></msub><mo>(</mo><mi>t</mi><mo>)</mo><mo>\unicode{x0003D}</mo><msub><mo>\unicode{x02211}</mo><mi>i</mi></msub><mrow><msub><mi>F</mi><mrow><mi>s</mi><mo>,</mo><mi>i</mi></mrow></msub><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mrow></mrow></math>$ for both the push and the growth simulations, where i is the number of nodes located within a specific part of the body surface; see schematics in Figure 5c. The main differences are evident within the stationary mature zone in the growing simulation and its equivalent region in the pushing simulation, where the pushed organ consistently experiences higher shear forces compared to the growing organ (gray columns). We also compare the mechanical work required for pushing and growing by measuring the sum of forces acting on the body surface nodes multiplied by the distances each node traveled during penetration:

$<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0013" wiley:location="equation/pce15089-math-0013.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><msup><mi>W</mi><mi mathvariant="italic">tot</mi></msup><mo>\unicode{x0003D}</mo><msub><mo>\unicode{x02211}</mo><mi>i</mi></msub><mrow><msub><mi>F</mi><mrow><mi>s</mi><mo>,</mo><mi>i</mi></mrow></msub><mo>\unicode{x022C5}</mo><msub><mrow><mi mathvariant="normal">\unicode{x00394}</mi><mi>y</mi></mrow><mi>i</mi></msub></mrow></mrow></mrow></math>$ . We find that growing demands approximately half the amount of work in comparison to pushing, across all friction values, suggesting that growing is energetically more efficient than pushing into a medium (Figure 5d). Increased friction at the interface increases the mechanical work for both growth and push penetration mechanisms, with a constant ratio.

3.4 Growing through the medium decreases the impact on the surrounding medium

To study the extent of the impact of growing vs pushing on the surrounding environment, we compute the propagation of displacements in the medium induced by the pushing/growing object. Figure 6a,b shows color maps of displacements for μ = 0.2, which extend farther around the pushed object compared to the growing one. This is evident in cross-sections of both the top view (Figure 6a and Supporting Information S1: Video S3) and side view (Figure 6b, and Supporting Information S1: Video S4). These findings also hold for μ = 0.3, with minor differences observed for the lowest friction, μ = 0.05 (see Supporting Information S1: Figure S12). To quantitatively address the evolution of these differences over time, we focused on two fixed rectangular regions in the agar domain (of a width of one quarter of the organ length which is in contact with the agar at the final time point, and a length equal to the radius of the agar domain, see Supporting Information S1: Figure S13 for a detailed description): one extending from the static mature zone (Figure 6c) and the other from the growth zone (Figure 6d), and their equivalent regions in the pushing simulations where no elongation occurs. At each time point, we compute the average displacements within these regions $<math altimg="urn:x-wiley:01407791:media:pce15089:pce15089-math-0014" wiley:location="equation/pce15089-math-0014.png" xmlns="http://www.w3.org/1998/Math/MathML"><mrow><mrow><msub><mi>U</mi><mi mathvariant="italic">avg</mi></msub><mo>(</mo><mi>t</mi><mo>)</mo><mo>\unicode{x0003D}</mo><mfrac><mn>1</mn><mi>n</mi></mfrac><msubsup><mo>\unicode{x02211}</mo><mrow><mi>i</mi><mo>\unicode{x0003D}</mo><mn>1</mn></mrow><mi>n</mi></msubsup><mrow><msub><mi>U</mi><mi>i</mi></msub><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mrow></mrow></math>$ for both penetration mechanisms, where i is a node located within the region and n is the number of nodes in this region. Average displacements are computed for different friction levels and are then normalized by the average displacement at the tip displacement of 0.52 mm for the pushed organ with μ = 0.3 (Figure 6c,d). Actual values with no normalization are brought in the insets. As expected, similar displacements are observed in both regions for tip penetration of up to 0.2 mm. However, for larger penetration values, when the mature zone begins to form, pushing leads to higher agar displacements. This difference is particularly pronounced in the vicinity of the mature zone, where displacements plateau for the growing mechanism, in contrast to the pushing mechanism where displacements continue to increase (Figure 6c). Within the growth zone region, differences between push and growth are less pronounced (Figure 6d). The raw plots, with no normalization (Figure 6c-d, insets) show that at a certain tip penetration (~0.3–0.4 mm; depending on the friction) displacements around the growth zone exceed those around the mature zone, that is the front part of the penetrating body has a more pronounced impact on the surrounding medium as penetration increases. In general, higher friction in the root/agar interface increases the differences between pushing and growing.

4 DISCUSSION

In this study, we studied the benefits of the growth-driven penetration mechanism employed by plant roots, compared to commonly-used push-driven mechanisms, in terms of mechanical interactions and deformation of the surrounding medium. We measured and compared the displacements within an agar gel induced by the penetration of a growing Arabidopsis thaliana root to those of a pushed needle. To measure the micro-scale deformations in the medium, we combined confocal microscopy imaging and tracking analysis using a DVC method (Bao et al., 2018; Franck et al., 2007, 2011; Keyes et al., 2016, 2017; Lesman et al., 2014; Vollsnes et al., 2010; von Wangenheim et al., 2017). Experiments revealed that the pushed needle leads to larger deformations in the agar compared to the growing root (Figure 2). Due to technical limitations, the insertion speed of the needle was faster than the root growth rate. In a viscoelastic gel, the loading rate can affect the gel's mechanical response, with higher speed leading to effectively stiffer material and thus reduced deformation (Ed-daoui and Snabre, 2021). In our system, we believe that the effect of penetration speed is negligible since the time elapsed between two successive measurements in the needle experiment (30 min) was longer than the relaxation time (~15 min). In addition, the relatively high speed of the needle can cause the gel to become more rigid, which in turn may lead to a decrease in the displacement field. Thus, the measured differences in the gel displacements between the needle and the root in case of a slower insertion speed of the needle could increase rather than decrease. Motivated by these results, we developed a FE model to identify the mechanisms underpinning these differences. We ran simulations, informed by experimental parameters, and found that growth-driven penetration reduces frictional forces and mechanical work, and causes lower displacements in the surrounding environment compared to the push-driven mechanism. These findings are in line with Sadeghi et al. who showed that a self-growing robot, based on additive manufacturing, penetrated granular substrates using up to 50% less force compared to pushing it (Sadeghi et al., 2013). Mechanical interactions are due to friction, and therefore the movement of the body relative to its surrounding medium. While in the case of a pushed rod the entire body moves against its surroundings, in the case of growing roots only the tip and subapical growth zone move, and the static mature zone does not move. Therefore, new deformations occur only at the front part of the root, and cease to develop as the growth zone becomes mature, and therefore stationary. Conversely, when an object is pushed, forces arise from the continuous movement of the entire object, intensifying frictional forces with the domain walls (Jushiddi et al., 2019). As a result, agar displacements stemming from the pushed object are more substantial and propagate over a greater distance compared to those produced by a growing object.

We note here that we employed a minimal model which captures the dominant characteristics of the problem. However, future studies will explore more intricate material models, such as modeling failure by crack propagation or material rupture (Assaad et al., 2015; Misra et al., 1986; Oldfield et al., 2013; Yamaguchi et al., 2018), characterizing the gel as a viscoelastic fluid adopting a Coupled Eulerian-Lagrangian (CEL)-based FE method for dynamic analysis during the insertion of an object into the medium (Jushiddi et al., 2019). We also adopted a minimal model of root growth, and future work may include further biological factors which may promote penetration, for example, lateral roots and root hairs behind the growth zone, which provide anchorage, and mucilage secretion or sloughing cells at the cap, which lubricate the root surface and decrease friction at the root-soil interface (Sadeghi et al., 2014; Sadeghi et al., 2017; Tomobe et al., 2023; Vollsnes et al., 2010).

In all, we find that not only is a growing object energetically more efficient than its pushed counterpart, but that it also leads to a smaller range of deformations, thereby minimizing the environmental disruption it causes to its surroundings. These findings may impact a number of fields. In the context of thigmotropism, the root's ability to actively respond to contact and overcome physical barriers (Kolb et al., 2017; Porat et al., 2023; von Wangenheim et al., 2017; Yamaguchi et al., 2018), this deformation range can be thought of as effectively increasing a root's presence in the medium, perhaps allowing a neighboring root to sense it through medium deformation—before direct physical contact. Moreover, our findings may provide bio-mimetic solutions for the development of a new generation of growth-driven penetrating devices as an alternative to the traditional push-driven devices, both for soil penetration, as well as for surgical procedures. Indeed, a common goal of many medical intervention surgeries that use catheters, endoscopic devices or biopsy needles is to penetrate complex, curved paths while attempting to minimally damage the surrounding tissue (Assaad et al., 2015; Jushiddi et al., 2019), for example neurosurgical scenarios (Audette et al., 2020).

ACKNOWLEDGEMENTS

We thank Sari Natan for her help with the confocal microscope in the root experiments. Yasmine Meroz acknowledges funding from: Israel Science Foundation Grant 2307/22. Yasmine Meroz and Ayelet Lesman acknowledge funding from the Zimin Institute for Engineering Solutions Advancing Better Lives.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflict of interest.

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information

REFERENCES

Ani, A.O., Mbajiorgu, C.C., Akubuo, C.O. & Onwualu, P.A. (2011) A proctor cone penetrometer for in-situ soil strength studies in Nigeria. International Journal of Agricultural and Biological Engineering, 4, 16–25.
Google Scholar
Assaad, W., Jahya, A., Moreira, P. & Misra, S. (2015) Finite-element modeling of a bevel-tipped needle interacting with gel. Journal of Mechanics in Medicine and Biology, 15, 1550079.
10.1142/S0219519415500797
Google Scholar
Audette, M.A., Bordas, S.P. & Blatt, J.E. (2020) Robotically steered needles: a survey of neurosurgical applications and technical innovations. Robotic Surgery: Research and Reviews, 7, 1–23.
10.2147/RSRR.S224446
PubMed Google Scholar
Bao, T., Melenka, G.W., Ljubotina, M.K., Carey, J.P. & Cahill, J.F. (2018) A new method for the rapid characterization of root growth and distribution using digital image correlation. New Phytologist, 218, 835–846.
10.1111/nph.15009
CAS PubMed Web of Science® Google Scholar
Bastien, R., Douady, S. & Moulia, B. (2014) A unifying modeling of plant shoot gravitropism with an explicit account of the effects of growth. Frontiers in Plant Science, 5, 1–9.
10.3389/fpls.2014.00136
Google Scholar
Beemster, G.T.S. & Baskin, T.I. (1998) Analysis of cell division and elongation underlying the developmental acceleration of root growth in Arabidopsis thaliana. Plant Physiology, 116, 1515–1526.
10.1104/pp.116.4.1515
CAS PubMed Web of Science® Google Scholar
Bengough, A.G., Bransby, M.F., Hans, J., McKenna, S.J., Roberts, T.J. & Valentine, T.A. (2006) Root responses to soil physical conditions; growth dynamics from field to cell. Journal of Experimental Botany, 57, 437–447.
10.1093/jxb/erj003
CAS PubMed Web of Science® Google Scholar
Bidhendi, A.J. & Geitmann, A. (2018) Finite element modeling of shape changes in plant cells. Plant Physiology, 176, 41–56.
10.1104/pp.17.01684
CAS PubMed Web of Science® Google Scholar
Bull, D.J., Smethurst, J.A., Sinclair, I., Pierron, F., Roose, T., Powrie, W. et al. (2020) Mechanisms of root reinforcement in soils: an experimental methodology using four-dimensional x-ray computed tomography and digital volume correlation. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 476, 1–23.
10.1098/rspa.2019.0838
Google Scholar
Calusi, B., Tramacere, F., Gualtieri, S., Pugno, N.M. & Mazzolai, B. (2020) Plant root penetration and growth as a mechanical inclusion problem. International Journal of Non-Linear Mechanics, 120, 103344.
10.1016/j.ijnonlinmec.2019.103344
Web of Science® Google Scholar
Chelakkot, R. & Mahadevan, L. (2017) On the growth and form of shoots. Journal of the Royal Society Interface, 14, 20170001.
10.1098/rsif.2017.0001
PubMed Google Scholar
Clark, L.J., Whalley, W.R. & Barraclough, P.B. (2003) How do roots penetrate strong soil? Plant and Soil, 255, 93–104.
10.1023/A:1026140122848
CAS Web of Science® Google Scholar
Darwin, C. & Darwin, F. (1880) The Power of Movement in Plants. Cambridge University Press.
10.5962/bhl.title.102319
Google Scholar
Delaine-Smith, R.M., Burney, S., Balkwill, F.R. & Knight, M.M. (2016) Experimental validation of a flat punch indentation methodology calibrated against unconfined compression tests for determination of soft tissue biomechanics. Journal of the Mechanical Behavior of Biomedical Materials, 60, 401–415.
10.1016/j.jmbbm.2016.02.019
CAS PubMed Web of Science® Google Scholar
Dupuy, L., Fourcaud, T. & Stokes, A. (2005) A numerical investigation into the influence of soil type and root architecture on tree anchorage. Plant and Soil, 278, 119–134.
10.1007/s11104-005-7577-2
CAS Web of Science® Google Scholar
Ed-daoui, A. & Snabre, P. (2021) Poroviscoelasticity and compression-softening of agarose hydrogels. Rheologica Acta, 60, 327–351.
10.1007/s00397-021-01267-3
CAS Google Scholar
Fayant, P., Girlanda, O., Chebli, Y., Aubin, C.É., Villemure, I. & Geitmann, A. (2010) Finite element model of polar growth in pollen tubes. The Plant Cell, 22, 2579–2593.
10.1105/tpc.110.075754
CAS PubMed Web of Science® Google Scholar
Franck, C., Hong, S., Maskarinec, S.A., Tirrell, D.A. & Ravichandran, G. (2007) Three-dimensional full-field measurements of large deformations in soft materials using confocal microscopy and digital volume correlation. Experimental Mechanics, 47, 427–438.
10.1007/s11340-007-9037-9
Web of Science® Google Scholar
Franck, C., Maskarinec, S.A., Tirrell, D.A. & Ravichandran, G. (2011) Three-dimensional traction force microscopy: a new tool for quantifying cell-matrix interactions. PLoS One, 6, e17833.
10.1371/journal.pone.0017833
CAS PubMed Web of Science® Google Scholar
Ganju, E., Han, F., Prezzi, M., Salgado, R. & Pereira, J.S. (2020) Quantification of displacement and particle crushing around a penetrometer tip. Geoscience Frontiers, 11, 389–399.
10.1016/j.gsf.2019.05.007
Google Scholar
Gliński, J. & Lipiec, J. (2018) Soil physical conditions and plant roots.
10.1201/9781351076708
Google Scholar
Goriely, A. (2017) The mathematics and mechanics of biological growth, 1st ed. Springer US.
10.1007/978-0-387-87710-5
Google Scholar
Hawkes, E.W., Blumenschein, L.H., Greer, J.D. & Okamura, A.M. (2017) A soft robot that navigates its environment through growth. Science Robotics, 2, 1–8.
10.1126/scirobotics.aan3028
Web of Science® Google Scholar
Herrick, J.E. & Jones, T.L. (2002) A dynamic cone penetrometer for measuring soil penetration resistance. Soil Science Society of America Journal, 66, 1320–1324.
10.2136/sssaj2002.1320
CAS Web of Science® Google Scholar
Hobson, E.C., Li, W., Juliar, B.A., Putnam, A.J., Stegemann, J.P. & Deng, C.X. (2021) Resonant acoustic rheometry for non-contact characterization of viscoelastic biomaterials. Biomaterials, 269, 120676.
10.1016/j.biomaterials.2021.120676
CAS PubMed Google Scholar
Jin, W., Aufrecht, J., Patino-Ramirez, F., Cabral, H., Arson, C. & Retterer, S.T. (2020) Modeling root system growth around obstacles. Scientific Reports, 10, 15868.
10.1038/s41598-020-72557-8
CAS PubMed Web of Science® Google Scholar
Jushiddi, M.G., Mulvihill, J.J.E., Chovan, D., Mani, A., Shanahan, C., Silien, C. et al. (2019) Simulation of biopsy bevel-tipped needle insertion into soft-gel. Computers in Biology and Medicine, 111, 103337.
10.1016/j.compbiomed.2019.103337
PubMed Google Scholar
Kataoka, H., Noda, S., Yokota, H., Takagi, S., Himeno, R. & Okazawa, S. (2008) Simulations of needle insertion by using a Eulerian hydrocode FEM and the experimental validations, Medical Image Computing and Computer-Assisted Intervention–MICCAI 2008 Conference Proceedings, Springer Berlin Heidelberg, 560–568.
10.1007/978-3-540-85990-1_67
Google Scholar
Keyes, S.D., Cooper, L., Duncan, S., Koebernick, N., McKay Fletcher, D.M., Scotson, C.P. et al. (2017) Measurement of micro-scale soil deformation around roots using four-dimensional synchrotron tomography and image correlation. Journal of the Royal Society Interface, 14, 20170560.
10.1098/rsif.2017.0560
PubMed Web of Science® Google Scholar
Keyes, S.D., Gillard, F., Soper, N., Mavrogordato, M.N., Sinclair, I. & Roose, T. (2016) Mapping soil deformation around plant roots using in vivo 4D x-ray computed tomography and digital volume correlation. Journal of Biomechanics, 49, 1802–1811.
10.1016/j.jbiomech.2016.04.023
CAS PubMed Web of Science® Google Scholar
Kirby, J.M. & Bengough, A.G. (2002) Influence of soil strength on root growth: experiments and analysis using a critical-state model. European Journal of Soil Science, 53, 119–127.
10.1046/j.1365-2389.2002.00429.x
Web of Science® Google Scholar
Kolb, E., Legué, V. & Bogeat-Triboulot, M.-B. (2017) Physical root—soil interactions. Physical Biology, 14, 065004–065029.
10.1088/1478-3975/aa90dd
PubMed Web of Science® Google Scholar
Lesman, A., Notbohm, J., Tirrell, D.A. & Ravichandran, G. (2014) Contractile forces regulate cell division in three-dimensional environments. Journal of Cell Biology, 205, 155–162.
10.1083/jcb.201309029
CAS PubMed Web of Science® Google Scholar
Liyanapathirana, D.S. (2009) Arbitrary Lagrangian Eulerian based finite element analysis of cone penetration in soft clay. Computers and Geotechnics, 36, 851–860.
10.1016/j.compgeo.2009.01.006
Web of Science® Google Scholar
Lockhart, J.A. (1965) An analysis of irreversible plant cell elongation. Journal of Theoretical Biology, 8, 264–275.
10.1016/0022-5193(65)90077-9
CAS PubMed Web of Science® Google Scholar
Meder, F., Baytekin, B., Del Dottore, E., Meroz, Y., Tauber, F., Walker, I. et al. (2023) A perspective on plant robotics: from bioinspiration to hybrid systems. Bioinspiration & Biomimetics, 18, 015006.
10.1088/1748-3190/aca198
Google Scholar
Misra, R.K., Dexter, A.R. & Alston, A.M. (1986) Maximum axial and radial growth pressures of plant roots. Plant and Soil, 95, 315–326.
10.1007/BF02374612
Web of Science® Google Scholar
Nayar, V.T., Weiland, J.D., Nelson, C.S. & Hodge, A.M. (2012) Elastic and viscoelastic characterization of agar. Journal of the Mechanical Behavior of Biomedical Materials, 7, 60–68.
10.1016/j.jmbbm.2011.05.027
CAS PubMed Web of Science® Google Scholar
Oldfield, M., Dini, D., Giordano, G. & Rodriguez y Baena, F. (2013) Detailed finite element modelling of deep needle insertions into a soft tissue phantom using a cohesive approach. Computer Methods in Biomechanics and Biomedical Engineering, 16, 530–543.
10.1080/10255842.2011.628448
PubMed Web of Science® Google Scholar
Peinke, I., Hagenmuller, P., Andò, E., Chambon, G., Flin, F. & Roulle, J. (2020) Experimental study of cone penetration in snow using X-Ray tomography. Frontiers in Earth Science, 8, 1–17.
10.3389/feart.2020.00063
Google Scholar
Porat, A., Riviere, M. & Meroz, Y. (2024) A quantitative model for spatio-temporal dynamics of root gravitropism. Journal of Experimental Botany, 75, 620–630.
10.1093/jxb/erad383
CAS PubMed Google Scholar
Porat, A., Tedone, F., Palladino, M., Marcati, P. & Meroz, Y. (2020) A general 3D model for growth dynamics of sensory-growth systems: from plants to robotics. Frontiers in Robotics and AI, 7, 1–14.
10.3389/frobt.2020.00089
PubMed Google Scholar
Porat, A., Tekinalp, A., Bhosale, Y., Gazzola, M. & Meroz, Y. (2023) On the mechanical origins of waving, coiling and skewing in Arabidopsis thaliana roots. Proceedings of the National Academy of Sciences, 121, 541081.
Google Scholar
Ruiz, S., Straub, I., Schymanski, S.J. & Or, D. (2016) Experimental evaluation of earthworm and plant root soil penetration-cavity expansion models using cone penetrometer analogs. Vadose Zone Journal, 15, 1–14.
10.2136/vzj2015.09.0126
Google Scholar
Sadeghi, A., Mondini, A. & Mazzolai, B. (2017) Toward self-growing soft robots inspired by plant roots and based on additive manufacturing technologies. Soft Robotics, 4, 211–223.
10.1089/soro.2016.0080
PubMed Web of Science® Google Scholar
Sadeghi, A., Tonazzini, A., Popova, L. & Mazzolai, B. (2013) Robotic mechanism for soil penetration inspired by plant root. IEEE International Conference on Robotics and Automation, Conference Proceedings, 3457–3462.
Google Scholar
Sadeghi, A., Tonazzini, A., Popova, L. & Mazzolai, B. (2014) A novel growing device inspired by plant root soil penetration behaviors. PLoS One, 9, e90139.
10.1371/journal.pone.0090139
PubMed Web of Science® Google Scholar
Schnepf, A., Leitner, D., Landl, M., Lobet, G., Mai, T.H. & Morandage, S. et al. (2018) CRootBox: a structural-functional modelling framework for root systems. Annals of Botany, 121, 1033–1053.
10.1093/aob/mcx221
PubMed Web of Science® Google Scholar
Seidel, S.J., Gaiser, T., Srivastava, A.K., Leitner, D., Schmittmann, O. & Athmann, M. et al. (2022) Simulating root growth as a function of soil strength and yield with a field-scale crop model coupled with a 3D architectural root model. Frontiers in Plant Science, 13, 1–19.
10.3389/fpls.2022.865188
Google Scholar
Silverberg, J.L., Noar, R.D., Packer, M.S., Harrison, M.J., Henley, C.L., Cohen, I. et al. (2012) 3D imaging and mechanical modeling of helical buckling in medicago truncatula plant roots. Proceedings of the National Academy of Sciences, 109, 16794–16799.
10.1073/pnas.1209287109
CAS PubMed Web of Science® Google Scholar
SIMULIA (2014) Abaqus/CAE 6.14 user's manual. SIMULIA.
Google Scholar
Sipos, A.A. & Várkonyi, P.L. (2022) A unified morphoelastic rod model with application to growth-induced coiling, waving, and skewing of plant roots. Journal of the Mechanics and Physics of Solids, 160, 104789.
10.1016/j.jmps.2022.104789
Google Scholar
Stubbs, C.J., Cook, D.D. & Niklas, K.J. (2019) A general review of the biomechanics of root anchorage. Journal of Experimental Botany, 70, 3439–3451.
10.1093/jxb/ery451
CAS PubMed Web of Science® Google Scholar
Taiz, L., Zeiger, E., Møller, I.M. & Murphy, A. (2014) Plant physiology and development, 6th edition, Sinauer Associates, Oxford University Press.
Google Scholar
Thompson, M.V. & Holbrook, N.M. (2004) Root-gel interactions and the root waving behavior of arabidopsis. Plant Physiology, 135, 1822–1837.
10.1104/pp.104.040881
CAS PubMed Web of Science® Google Scholar
Tolooiyan, A. & Gavin, K. (2011) Modelling the cone penetration test in sand using cavity expansion and arbitrary lagrangian eulerian finite element methods. Computers and Geotechnics, 38, 482–490.
10.1016/j.compgeo.2011.02.012
Web of Science® Google Scholar
Tomobe, H., Tsugawa, S., Yoshida, Y., Arita, T., Tsai, A.Y.L., Kubo, M. et al. (2023) A mechanical theory of competition between plant root growth and soil pressure reveals a potential mechanism of root penetration. Scientific Reports, 13, 7473.
10.1038/s41598-023-34025-x
CAS PubMed Google Scholar
Tonazzini, A., Sadeghi, A., Popova, L. & Mazzolai, B. (2013) Plant root strategies for robotic soil penetration, Biomimetic and Biohybrid Systems: Second International Conference, Living Machines 2013, London, UK, July 29–August 2, 2013. Proceedings 2. Springer Berlin Heidelberg, 447–449.
10.1007/978-3-642-39802-5_62
Google Scholar
Topakci, M., Unal, I., Canakci, M., Celik, H.K. & Karayel, D. (2010) Design of a horizontal penetrometer for measuring on-the-go soil resistance. Sensors, 10, 9337–9348.
10.3390/s101009337
Google Scholar
Trinh, D.C., Alonso-Serra, J., Asaoka, M., Colin, L., Cortes, M., Malivert, A. et al. (2021) How mechanical forces shape plant organs. Current Biology, 31, R143–R159.
10.1016/j.cub.2020.12.001
CAS PubMed Web of Science® Google Scholar
Vollsnes, A.V., Futsaether, C.M. & Bengough, A.G. (2010) Quantifying rhizosphere particle movement around mutant maize roots using time-lapse imaging and particle image velocimetry. European Journal of Soil Science, 61, 926–939.
10.1111/j.1365-2389.2010.01297.x
Web of Science® Google Scholar
von Wangenheim, D., Hauschild, R., Fendrych, M., Barone, V., Benková, E. & Friml, J. (2017) Live tracking of moving samples in confocal microscopy for vertically grown roots. eLife, 6, 1–20.
Google Scholar
Wei, L., Abu-Farsakh, M.Y. & Tumay, M.T. (2005) Finite-element analysis of inclined piezocone penetration test in clays. International Journal of Geomechanics, 5, 167–178.
10.1061/(ASCE)1532-3641(2005)5:3(167)
Google Scholar
Wooten, M.B. & Walker, I.D. (2018) Vine-inspired continuum tendril robots and circumnutations. Robotics, 7, 58.
10.3390/robotics7030058
Web of Science® Google Scholar
Yamaguchi, T., Sato, R. & Sawae, Y. (2018) Propagation of fatigue cracks in friction of brittle hydrogels. Gels, 4, 53.
10.3390/gels4020053
PubMed Google Scholar
Yanagisawa, M., Desyatova, A.S., Belteton, S.A., Mallery, E.L., Turner, J.A. & Szymanski, D.B. (2015) Patterning mechanisms of cytoskeletal and cell wall systems during leaf trichome morphogenesis. Nature Plants, 1, 15014.
10.1038/nplants.2015.14
CAS PubMed Web of Science® Google Scholar

Citing Literature

Volume47, Issue12

December 2024

Pages 5076-5088

Filename	Description
pce15089-sup-0001-20240627_Manuscript_SI_Final_clean.docx5.2 MB	Supporting information.
pce15089-sup-0002-movieS1_animation_of_growth.mp4724.6 KB	Supporting information.
pce15089-sup-0003-movieS2_contact_forces_fric02_push_growth_side_section_view.mp42 MB	Supporting information.
pce15089-sup-0004-movieS3_displacements_fric02_push_growth_top_view.mp4658.2 KB	Supporting information.
pce15089-sup-0005-movieS4_displacements_fric02_push_growth_side_section_view.mp43.3 MB	Supporting information.

Analysis of root-environment interactions reveals mechanical advantages of growth-driven penetration of roots

Abstract

1 INTRODUCTION