18O enrichment of sucrose and photosynthetic and nonphotosynthetic leaf water in a C3 grass—atmospheric drivers and physiological relations
Abstract
The 18O enrichment (Δ18O) of leaf water affects the Δ18O of photosynthetic products such as sucrose, generating an isotopic archive of plant function and past climate. However, uncertainty remains as to whether leaf water compartmentation between photosynthetic and nonphotosynthetic tissue affects the relationship between Δ18O of bulk leaf water (Δ18OLW) and leaf sucrose (Δ18OSucrose). We grew Lolium perenne (a C3 grass) in mesocosm-scale, replicated experiments with daytime relative humidity (50% or 75%) and CO2 level (200, 400 or 800 μmol mol−1) as factors, and determined Δ18OLW, Δ18OSucrose and morphophysiological leaf parameters, including transpiration (Eleaf), stomatal conductance (gs) and mesophyll conductance to CO2 (gm). The Δ18O of photosynthetic medium water (Δ18OSSW) was estimated from Δ18OSucrose and the equilibrium fractionation between water and carbonyl groups (εbio). Δ18OSSW was well predicted by theoretical estimates of leaf water at the evaporative site (Δ18Oe) with adjustments that correlated with gas exchange parameters (gs or total conductance to CO2). Isotopic mass balance and published work indicated that nonphotosynthetic tissue water was a large fraction (~0.53) of bulk leaf water. Δ18OLW was a poor proxy for Δ18OSucrose, mainly due to opposite Δ18O responses of nonphotosynthetic tissue water (Δ18Onon-SSW) relative to Δ18OSSW, driven by atmospheric conditions.
1 INTRODUCTION
Leaf water is enriched in 18O relative to source water, the water taken up by plants through their root systems (Barbour, 2007; Farquhar et al., 2007). This 18O enrichment of bulk leaf water (Δ18OLW, for definitions and specifications of symbols, see Table 1) is determined by environmental and biological factors (Barbour et al., 2021; Cernusak et al., 2016, 2022; Ferrio et al., 2012; Helliker & Ehleringer, 2000; 2002; Hirl et al., 2019; Holloway-Phillips et al., 2016). The 18O enrichment of leaf water also affects the 18O enrichment of primary photosynthetic products, such as sucrose (Cernusak et al., 2003, 2005; Lehmann et al., 2017), the most widely distributed transport sugar and primary substrate for metabolism in plants, including in grasses (Braun et al., 2014; Lalonde et al., 2003; Lattanzi et al., 2012). Although mechanistic understanding of the biological controls of Δ18OLW and their relationship with 18O enrichment of sucrose (Δ18OSucrose) is still imperfect, it is known that they determine an organic isotopic signal of plant function and past climate, motivating interest of a wide range of scientific disciplines from paleoecology to bioclimatology, crop physiology, ecophysiology and plant biochemistry (Barbour, 2007; Siegwolf et al., 2022). Here, our interest is to better understand the physiological controls of Δ18OLW and its relationship with Δ18OSucrose in perennial ryegrass (Lolium perenne L.), a model C3 grass species of high economic value (Chapman et al., 2017).
| Symbol | Definition | Specification |
|---|---|---|
| δ18OX (or δ2HX) | The relative abundance of 18O (or 2H) in a sample X (source water, bulk leaf water or water in the LGDZ) calculated as δ18OX (or δ2HX = RX/Rs – 1, with RX and Rs the molar abundance ratios, 18O/16O (or 2H/1H), of the sample and of VSMOW | Tissue water in the LGDZ was collected as in Liu et al. (2017) |
| δ18OSource or δ2HSource | The flux-weighted average δ18O/δ2H of the water taken up by the root system of a plant, often termed δ18O/δ2H of xylem water | δ18O of nutrient solution (−9.7 ± 0.2‰ SD); δ2H of nutrient solution (−70.1 ± 1.2‰ SD) |
| δ18OVapour or δ2HVapour | The δ18O/or δ2H of vapour as measured above the canopy | δ18OVapour/δ2HVapour: constant across experimental runs and treatments, but more enriched during the dark period (δ18O = −14.2‰ ± 0.5‰ SD; δ2H = −104.6‰ ± 3.8‰ SD) than during the light period (δ18O = −15.2‰ ± 0.6‰ SD; δ2H = −109.6‰ ± 4.4‰ SD) |
| Δ18OX | The 18O enrichment above source water of a sample X (leaf water, LGDZ water, sucrose or vapour) calculated as Δ18OX = (δ18OX – δ18OSource)/(1 + δ18OSource) | |
| Δ18OLW | The Δ18O of bulk leaf blade water | |
| Δ18OSSW | The Δ18O of medium water at the site of photosynthesis and associated sucrose synthesis water | Estimated as Δ18OSucrose − εbio |
| Δ18Onon-SSW | The Δ18O of water in the total nonphotosynthetic fraction of the leaf blade | Calculated by isotopic mass balance (Equation 15, Δ18Onon-SSW = (Δ18OLW − fSSW Δ18OSSW)/fnon-SSW) using replicate-specific data of Δ18OLW, Δ18OSSW and estimates of the nonphotosynthetic bulk leaf water fraction (fnon-SSW) of Lolium perenne leaf blades |
| εbio | The average biochemical fractionation between carbonyl oxygen and water | 26.7‰, according to the temperature dependence of εbio for cellulose synthesis in aquatic plants as reported by Sternberg and Ellsworth (2011); constant for all treatments and closely similar to the constant εbio = 27‰ used in most studies (Barbour, 2007) |
| Δ18Oe | Theoretical estimate of the transpiration-weighted Δ18O at the evaporative site of whole-leaf blades (Farquhar & Gan, 2003) | Estimated using Equation 1: Δ18Oe ≈ ε+ + εk + (Δ18OVapour – εk) wa/wi, assuming: cuticular transpiration did not occur, stomatal conductance was nonpatchy and there were no gradients in leaf temperature, relative humidity and stomatal conductance inside the canopies |
| ε+ | The equilibrium fractionation between liquid and vapour phase | Estimated according to Majoube (1971): , with T the measured leaf temperature |
| εk | The kinetic fractionation during diffusion of water vapour through the leaf boundary layer and stomata | Calculated as in Farquhar et al. (1989) , with rs and rb the stomatal and boundary layer resistances, respectively (inverses of stomatal and boundary layer conductances) |
| wa/wi | The ratio of the water vapour mole fractions in the air outside the leaf boundary layer and at the evaporative sites inside the leaf | |
| φX | The proportional difference between Δ18OX (the Δ18O of a sample X) and Δ18Oe (i.e., φX = 1 – Δ18OX/Δ18Oe), with X representing either bulk leaf blade, SSW or non-SSW water | |
| L | The effective path length of liquid water transport through the leaf | Calculated by solving Equations 4 and 7: L = ℘CD/E, , with E the transpiration rate, C the molar concentration of water and D the diffusivity of heavy water (H218O) in water |
| fx; (1 – fx) | The fraction of vein water in bulk leaf water; (1 – fx) the remaining leaf water | |
| fSSW; fnon-SSW | The photosynthetic (and sucrose synthesis) water (SSW) and nonphotosynthetic water (non-SSW) fractions of bulk leaf blade water (fnon-SSW = 1 – fSSW) | fnon-SSW = 0.53 estimated as the fraction of nonmesophyll water in bulk leaf blade water of L. perenne according to published leaf anatomy data (Charles-Edwards et al., 1974; Dengler et al., 1994) and used in Equation 6 under the standard assumption of a well-mixed mesophyll. In a sensitivity analysis (Figure 4, see also Figure 7) we also used fnon-SSW = 0.70 and 0.88 to assess putative effects of a nonfully-mixed mesophyll |
| Stomatal conductance to H2O | From leaf level measurements under the same environmental conditions as in the growth chambers for each treatment | |
| Stomatal conductance to CO2 | As specified for , above | |
| gm | Mesophyll conductance to CO2 | Estimated using the 13C discrimination method (Evans et al., 1986) during parallel gs and Eleaf measurements |
| gtotal | Total conductance for CO2, estimated as the sum of and gm | Calculated as 1/(1/ + 1/gm) |
| Eleaf | Leaf transpiration rate | From leaf level measurements under the same environmental conditions as in the growth chambers for each treatment |
- Abbreviations: LGDZ, leaf growth-and-differentiation zone; SD, standard deviation; SSW, sucrose synthesis water; VSMOW, Vienna standard mean ocean water.
Δ18OSucrose was first assessed systematically by Cernusak et al. (2003). During steady-state leaf cuvette measurements with Ricinus communis under a range of evaporative conditions, they found a virtually constant 27‰ 18O enrichment of phloem sap dry matter (which is mostly sucrose) relative to average lamina water, which is defined as bulk leaf water minus the water contained in the primary veins. This difference matched closely to expectations based on the equilibrium fractionation between water and carbonyl groups (the biochemical fractionation, εbio) obtained in comparisons of 18O in cellulose of aquatic plants and the water in which they grew (DeNiro & Epstein, 1981; Epstein et al., 1977; Yakir & DeNiro, 1990), and also in comparisons of acetone and water (Sternberg & DeNiro, 1983). Field studies with Eucalyptus globulus agreed with this finding, provided that the enrichment of average lamina water was flux-weighted over daily time scales using net CO2 assimilation rates (Cernusak et al., 2005). To our best knowledge, the relationship between Δ18OSucrose and the average lamina water of grasses has not been explored in detail. A few years ago, Lehmann et al. (2017) demonstrated that bulk leaf water of two C3 grasses (L. perenne L. and Dactylis glomerata L.) is less 18O enriched than the medium water where sucrose synthesis occurs (Δ18OSSW) when the latter was estimated as Δ18OSucrose—εbio, with εbio assumed to be constant at 27‰. Their investigations demonstrated a systematic underestimation of Δ18OSSW by Δ18OLW by 3.6‰–6.2‰ in the two species in a controlled environment study (note that Lehmann et al. used a definition of Δ18OSSW which was different from the present one, since they used the 18O enrichment above (bulk) leaf water rather than source water as used here). Interestingly, the offset between Δ18OSSW and Δ18OLW was higher at low (50%) than at high (75%) relative humidity (RH) of the air in the growth environment.
An offset between Δ18OSSW and Δ18OLW is of great interest, as it can inform us about the functional heterogeneity of 18O enrichment of bulk leaf water (Cernusak et al., 2003; Holloway-Phillips et al., 2016; Lehmann et al., 2017) and help us to improve our understanding of the biological mechanisms controlling Δ18O of photosynthetic and sucrose synthesis medium water (Δ18OSSW, Table 1) separately from nonphotosynthetic tissue water (Δ18Onon-SSW, Table 1) in the bulk leaf. Additionally, Δ18OSSW can be compared with the modelled 18O enrichment at the evaporative site (Δ18Oe, see below)—as already done by Cernusak et al. (2003) in R. communis—to test the alternative hypothesis that Δ18OSSW in grasses is closer to the 18O enrichment at the evaporative sites in leaves (Δ18Oe).
Equation 2 can be interpreted in terms of a two-pool model (Leaney et al., 1985; Song et al., 2015; Yakir et al., 1990) represented by a leaf having a certain fraction φLW of 18O unenriched (source) water in the veins (or vascular and associated ground tissue) and a remaining fraction 1 − φLW that has an 18O enrichment equal to that of the evaporating sites.
However, anatomical literature shows that fnon-SSW is much greater than fx (and, hence, fSSW is much smaller than 1 – fx), illustrating the fact that using Equation 7 allows a better accounting of the nonphotosynthetic fraction of bulk leaf water in the two-pool model. According to studies of Charles-Edwards et al. (1974) with L. perenne the vascular tissue (≈fx), including parenchyma extensions and bundle sheath, accounted for ~10% of the leaf cross-sectional area and ~12% of bulk leaf water, considering that intercellular air space accounts for ~30% of the mesophyll volume (Dengler et al., 1994). On the same basis, the epidermis accounted for ~41% and the mesophyll for ~47% of bulk leaf water content (LWC). On this basis, the sum of vascular tissue and epidermis (which together represent fnon-SSW) accounts for a total of ~53% of the bulk leaf water in L. perenne, mainly due to the dominant contribution of the epidermis. Considering that (1) hydraulic connections between mesophyll and surrounding tissue may be weak in grasses (or in other species with the same hydraulic design; Barbour et al., 2021; Zwieniecki et al., 2007), and (2) expectations from Equation 5, that is, that the mesophyll is well-mixed (cf eq. 9 in Holloway-Phillips et al., 2016), we hypothesize that Equation 7 is a useful abstraction of Δ18OLW based on Δ18O in its component photosynthetic (Δ18OSSW) and nonphotosynthetic tissue water fractions (Δ18Onon-SSW).
In this context, this work addresses five questions. First, it compares Δ18OSSW (estimated as Δ18OSucrose − εbio ignoring secondary isotope terms) with Δ18OLW in the C3 grass L. perenne, one of the model species used by Lehmann et al. (2017), to corroborate their finding of an RH-dependent mismatch between Δ18OSSW and Δ18OLW. Second, it analyzes the relationship between Δ18OSSW and Δ18Oe, to test the hypothesis that Δ18OSSW is more closely associated with Δ18Oe than with Δ18OLW in L. perenne, similar to the approach used by Cernusak et al. (2003) with a dicot species, R. communis. Third, we solve Equation 6 for Δ18Onon-SSW, using Δ18OLW, Δ18OSSW and the estimate of the fraction of nonphotosynthetic tissue water (fnon-SSW) of 0.53 (see above and Charles-Edwards et al., 1974; Dengler et al., 1994). In that, we also test the sensitivity of Δ18Onon-SSW to the assumption (in Equation 7) that the mesophyll is well-mixed, by including some mesophyll (e.g., mesophyll vacuole volume) in the non-SSW fraction. Fourth, we evaluate the proportional difference between estimates of Δ18Onon-SSW and Δ18Oe (φnon-SSW = 1 − Δ18Onon-SSW/Δ18Oe) and its sensitivity to the well-mixed mesophyll assumption. Finally, we explore the relationship between φSSW or φnon-SSW and physiological parameters (including transpiration and stomatal and mesophyll conductances) that have been implied previously as putative controls of φLW. In that, we also explore the idea that nonphotosynthetic leaf water displays a Péclet effect (based on Equation 7) and discuss possible implications for the sites of evaporation within leaves (Barbour et al., 2017; Barbour et al., 2021; Rockwell et al., 2014) in contrasting atmospheric CO2 concentration and daytime RH. This work made use of a fully replicated (n = 3–5) mesocosm-scale experiment described previously by Baca Cabrera et al. (2020) with L. perenne plants grown in sward-like conditions in a 2 × 3 factorial experiment with atmospheric CO2 concentration (200, 400 or 800 μmol mol−1) and daytime RH of 50% or 75%.
2 MATERIALS AND METHODS
2.1 Plant material and growth conditions
Perennial ryegrass (L. perenne, cv. ‘Acento’) plants were grown in four plant growth chambers (PGR15; Conviron) in a 16: 8 h day: night cycle (temperature 20/16°C), under a 3 × 2 factorial design: three atmospheric CO2 concentration levels (‘half-ambient’ = 200, ‘ambient' = 400 or ‘double-ambient’ = 800 μmol mol−1) and two daytime RH levels (low RH = 50%, high RH = 75%; nighttime RH was 75% for all treatments), as previously described in Baca Cabrera et al. (2020). In brief, L. perenne plants were grown individually in plastic tubes (350 mm height, 50 mm diameter) filled with washed quartz sand (0.3–0.8 mm grain size) and arranged in plastic containers (770 × 560 × 300 mm) at a density of 383 plants m−2. Plants were supplied four times a day with a Hoagland-type nutrient solution with reduced nitrate-N content. Light was supplied by cool-white fluorescent tubes and warm-white light-emitting diode (LED) bulbs with a constant photosynthetic photon flux density (PPFD) of 800 µmol m−2 s−1 at plant height during the 16 h-long light period. A total of five sequential experimental runs were performed, resulting in five chamber scale replicates for the so-called ‘reference treatment’ (400 μmol mol-1 CO2/50% RH) and three replicate mesocosm-scale runs for the other treatments.
CO2 and RH treatments were installed on the 13th day after seed imbibition. For this, the air supplied to the chambers was mixed from dry CO2-free air and 18O-enriched or 18O-depleted tank CO2, using mass flow controllers. 18O-enriched CO2 was obtained from CARBO Kohlensäurewerke and had a δ18OCO2 which ranged between 14.1‰ and 20.2‰ between individual cylinders; 18O-depleted CO2 was purchased from Linde AG and had a δ18OCO2 which ranged between −9.0‰ and −2.0‰ between individual cylinders. In each experimental run, treatments were run in duplicate, with one chamber receiving the 18O-depleted and the other chamber the 18O-enriched CO2. RH and temperature were controlled by the chamber control system (CMP6050; Conviron). CO2 concentration and RH were measured every 30 min by an infrared gas analyzer (IRGA; Li-840; Li-Cor) and never deviated more than ±5 μmol mol−1 and ±2.0% relative to the set nominal value, respectively. The δ18O of CO2 at the inlet and outlet of each growth chamber was measured as in Liu et al. (2016) with a continuous-flow isotope ratio mass spectrometer (IRMS) (Delta Plus, Finnigan MAT).
2.2 Sampling design and extraction of tissue water and sucrose
Plants from each chamber-scale replicate were sampled when plant canopies were closed (leaf area index >5, at 7–9 weeks after the beginning of the experiment). At that time, the morphometric traits of leaves were similar among treatments (Baca Cabrera et al., 2020). Sampling took place at c. 2 h before the end of the light and dark periods. In each replicate sampling, 12 plants were randomly selected, dissected and the sampled plant material of 6 plants pooled in 1 subsample (providing 2 subsamples per chamber and per sampling occasion). Additionally, we sampled other plants as described in Baca Cabrera et al. (2020), to estimate LWC (in mol m−2 leaf area) of young fully expanded leaf blades. LWC was obtained gravimetrically and normalized by the leaf area. The IMAGE J software (Schneider et al., 2012) was used for digital analysis.
For tissue water extraction, the two youngest fully expanded leaf blades and the leaf growth-and-differentiation zone (LGDZ, see Figure 1 in Baca Cabrera et al., 2020) of three mature tillers per plant were excised, sealed in 12 mL Exetainer vials (Labco), capped, wrapped with Parafilm and stored at –18°C until water extraction. Tissue water was extracted for 2 h using cryogenic vacuum distillation as in Liu et al. (2016).
For sucrose extraction, the youngest fully expanded leaf blades of another two mature tillers from the same plants were excised, placed into paper bags, frozen in liquid nitrogen, stored at −18°C until freeze-drying, milled and stored again at −18°C until sucrose extraction. Water-soluble carbohydrates were extracted from 50 mg aliquots of dry material and sucrose separated from other compounds using a preparative high-performance liquid chromatography (HPLC) technique according to Gebbing and Schnyder (2001).
Using separate samples for tissue water and sucrose extraction could theoretically lead to greater scatter in the relationship between δ18O of leaf water (δ18OLW) and sucrose (δ18OSucrose), an eventuality that we minimized by extensive subsampling.
2.3 Gas exchange measurements
Leaf gas exchange measurements were performed during a 2-week interval between weeks 7 and 9 as described in Baca Cabrera et al. (2020). In brief, net assimilation (A, μmol CO2 m−2 s−1), leaf transpiration (Eleaf, mmol H2O m−2 s−1) and stomatal conductance to water vapour or CO2 (, mol H2O m−2 s−1 or , mol CO2 m−2 s−1) were measured on 6–12 plants per treatment with a LI-6400xt (Li-Cor) portable CO2/H2O gas exchange system with a clamp-on leaf cuvette (2 × 3 cm), installed in a separate plant growth chamber (E15, Conviron). For measurements, individual plants were removed from their growth chamber, and the midsection of the youngest fully developed leaf blades of four tillers was enclosed in the leaf cuvette. A, gs and Eleaf were measured at a leaf temperature of 21°C (air temperature in the leaf cuvette ranged between c. 20.0–21.0°C) and a PPFD of 800 µmol m−2 s−1 and with CO2 concentration and RH in the leaf cuvette (sample chamber) set equal to the conditions in the original growth environment.
Air for the leaf cuvette was supplied by mixing CO2-free, dry air (with 21% O2) and tank CO2 (from Carbo Kohlensäurewerke or Linde AG, see Section 2.1) using mass flow controllers. Measurements were logged under steady-state conditions for stomatal conductance and water vapour concentration.
2.4 Mesophyll conductance to CO2
2.5 Isotope analysis
Water samples were analyzed by cavity ring-down spectroscopy as described in Liu et al. (2016). A total of 1 µL of a water sample was injected into an A0211 high-precision vapourizer coupled to an L2110-i-CRDS (both Picarro Inc.). Each sample was measured 5–12 times depending on memory effects. After every 15–25 samples, heavy and light laboratory water standards, spanning the range of δ18O values in the data set and previously calibrated against V-SMOW, V-GISP and V-SLAP, were measured for SMOW-scaling and possible drift correction. Analytical uncertainty (standard deviation, SD) was <0.2‰ and <1.0‰ for δ18O and δ2H, respectively.
Sucrose samples were measured by isotope ratio mass spectrometry (IRMS) as in Baca Cabrera et al. (2021). Each sample was measured against a laboratory working standard carbon monoxide gas, previously calibrated against a secondary isotope standard (IAEA-601, accuracy of calibration ±0.25‰ SD). Solid internal laboratory standards (cotton powder) were run each time after the measurement of four samples for possible drift correction and for SMOW-scaling. The precision (SD) for the laboratory standard was <0.3‰.
We also checked for possible fractionation effects during HPLC sucrose separation, by comparing untreated fine ground sucrose directly weighed into silver cups with the same sucrose obtained after passage through the HPLC column. For the latter, we prepared a standard-mix (containing fructan, sucrose, glucose and fructose in typical tissue concentrations) and collected the sucrose fraction eluting from the HPLC column. No difference was detected for δ18OSucrose of the untreated sucrose (30.8 ± 0.7‰ SD) compared with the sucrose from the standard-mix passed through the HPLC (31.0 ± 0.3‰ SD).
Additionally, δ18O and δ2H of water vapour in the growth chambers (δ18OVapour/δ2HVapour) was measured by cavity ring-down spectroscopy as described in Liu et al. (2016). Here, we measured δ18OVapour/δ2HVapour continuously for 2 weeks when canopies were closed, both during the light and the dark periods. δ18OVapour was constant across experimental runs and treatments but was c. 1‰ more enriched during the dark period (−14.2‰ ± 0.5‰ SD) than during the light period (−15.2‰ ± 0.6‰ SD). A similar behaviour was observed for δ2HVapour (−104.6‰ ± 3.8‰ SD during the dark period and −109.6‰ ± 4.4‰ SD during the light period).
2.6 Evaporative site 18O enrichment
The 18O enrichment of evaporative sites water above source water (∆18Oe) during the light period was calculated using the Craig–Gordon model (Craig & Gordon, 1965; Dongmann et al., 1974) as presented in Cernusak et al. (2016) and given in Equation 1. wa/wi was calculated based on daytime air temperature (20°C) and RH (50% or 75%) inside the chambers, and canopy surface temperature, which was estimated using measurements of six type T thermocouples (in-house, custom-made) attached to mature leaf blades across each canopy. ε+ and εk were calculated as in Cernusak et al. (2016) (see Table 1), with stomatal conductance and boundary layer conductance (gb) data obtained from leaf gas exchange measurements and rates of water loss from leaf replicas (Grace & Wilson, 1976) (gb ≈ 0.2 mol m−2 s−1 for all treatments), respectively. Calculation of Δ18Oe—as given here—makes the (customary) simplifying assumptions that cuticular transpiration did not occur, stomatal conductance was nonpatchy and there were no gradients in leaf temperature, RH and stomatal conductance between the base and the top of the canopies.
2.7 The fractions of leaf water in nonphotosynthetic leaf tissue and its 18O enrichment
According to isotopic mass balance, Δ18OLW is a mass-weighted average of the Δ18O of its photosynthetic (Δ18OSSW) and nonphotosynthetic (Δ18Onon-SSW) components, with fssw and fnon-SSW the mass fractions of photosynthetic and nonphotosynthetic leaf water (fnon-SSW = 1 − fSSW) (Equation 6). Δ18OLW was obtained experimentally as explained above, and Δ18OSSW was estimated as Δ18OSucrose − εbio, with εbio the 18O fractionation between carbonyl groups and water in which they are formed (Barbour, 2007). εbio (=26.7‰) was estimated from the temperature-dependence of εbio associated with cellulose synthesis in aquatic plants (Sternberg & Ellsworth, 2011; see also Hirl et al., 2021) and the nominal daytime air temperature in the growth chambers (including treatment-related offsets of canopy temperature in the calculation would not change the temperature-dependent εbio by more than ± 0.15‰). This estimate of εbio is also close to the (temperature-independent, constant) 27‰ which has been used most commonly in this type of analysis (Barbour, 2007; Lehmann et al., 2017).
To allow for and explore the uncertainty of this well-mixed mesophyll assumption, we also used higher values of fnon-SSW, which effectively treated part of the mesophyll (e.g., some or all the mesophyll vacuole volume) as a component of the nonmesophyll fraction, that is, reflecting a Δ18O equal to that of the nonmesophyll water (Δ18Onon-SSW). The most extreme scenario set fnon-SSW = 0.88, which would include the entire mesophyll vacuole volume in the nonmesophyll fraction. In this scenario, the photosynthetic leaf water fraction (fSSW) equaled 0.12 and was represented solely by the combined water volume fraction of the mesophyll cytosol and chloroplasts. The latter was calculated from the volume fraction of cytosol plus chloroplasts (26%) in mesophyll cells of barley leaves (Winter et al., 1993) as 0.26 × (1 − 0.53). As an intermediate scenario we used fnon-SSW = 0.70. These higher estimates of fnon-SSW were then used to analyze the sensitivity of Δ18Onon-SSW (Equation 15), φnon-SSW (=1 Δ18Onon-SSW/Δ18Oe) and effective path length (L; calculated by the Péclet effect model defined by Equation 7) to variation of fnon-SSW.
2.8 Data selection and statistics
In the first step, linear mixed models were fitted to test the effect of the diel period (day vs. night) on Δ18OLW (n = 160) and Δ18OSSW (n = 70). All available subsamples (pseudo-replicates) were included in the analysis, with the growth chamber and experimental run defined as the random factors. A small but significant diel trend between the end of the light period and the end of the dark period was detected for Δ18OLW, but not for Δ18OSSW (Supporting Information: Table S1). Therefore, we decided to: (1) pool day and night Δ18OSSW data together; and (2) only use Δ18OLW data obtained near the end of the light period for further calculations, under the assumptions that these values better reflect 18O enrichment processes during photosynthesis. Additionally, we calculated φLW and φnon-SSW (which are derived from Δ18OLW) using data obtained either near the end of the light or the dark period but observed only very small differences and no variation in the CO2 and RH statistical effects on these variables (Supporting Information: Figure S1), indicating that our data selection was reasonable for further analyses.
In a second step, canopy scale replicates were obtained by pooling all individual subsamples from each canopy (n = 3–5) and two-way analysis of variance (ANOVA) tests used to assess the effects of CO2, RH and their interaction on Δ18OLW, Δ18OSSW, Δ18Oe and all derived parameters. The same statistical analysis was used for the gas exchange parameters but based on individual leaf replicates (n = 6–12). Additionally, ordinary least-squares linear regressions were performed to test the relationship between the different parameters (using treatment averages). All statistical analyses were performed in R v.4.0.2 (R Core Team, 2022). The R packages nlme (Pinheiro et al., 2019) and ggplot2 (Wickham, 2016) were used for fitting linear mixed models and data plotting, respectively.
3 RESULTS
3.1 18O enrichment of bulk leaf water (Δ18OLW), photosynthetic tissue water (Δ18OSSW), evaporative site enrichment (Δ18Oe) and relations among them
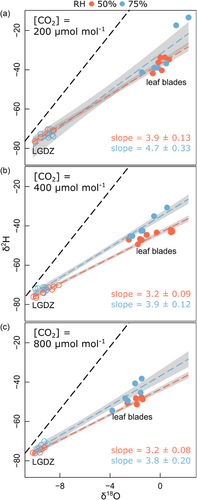
Δ18OLW determined near the end of the 16 h-long periods of constant light ranged between 7.9‰ and 10.2‰ and responded significantly to [CO2], with the increase of [CO2] from 200 to 800 μmol mol−1 causing decreases of Δ18OLW of 1.3‰ at a daytime RH of 50% (designated ‘low RH’ in the following) and 2.3‰ at a daytime RH of 75% (‘high RH’) (Table 2, Supporting Information: Figure S2). RH alone and the interaction of RH and [CO2] had no significant effects on Δ18OLW. Similar treatment effects (or their absence) were detected for Δ18OLW near the end of the dark period. However, Δ18OLW changed slightly more between the end of the light and the end of the dark period in the low than the high RH treatment, likely owing to the fact that the low RH treatment involved a 25%-increase of RH between the light and dark periods, while RH was kept constant in the high RH treatment. Overall, however, the changes of Δ18OLW between the end of the light and the end of the dark period were small (∼1.6‰ at low RH and ∼0.8‰ at high RH). These effects were consistent in replicated (n = 3–5) mesocosm-scale experiments. Although the absence of a significant daytime-RH effect on Δ18OLW was unexpected, plots of δ18O versus δ2H—made using end-of-the-light-period leaf water and leaf growth zone samples—demonstrated a significantly steeper slope (Figure 1) and a lower deuterium deviation with reference to the global meteoric water line (Supporting Information: Table S2) for the high RH compared with the low RH treatment, for all [CO2] levels, supporting a differential effect of daytime evaporative conditions on bulk leaf water isotope composition (Voelker et al., 2014) (see also discussion under Section 4.4).
| Parameter | Daytime RH (%) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 50 | 75 | ||||||||
| Atmospheric CO2 concentration (μmol mol−1) | Effect significance (p value) | ||||||||
| 200 | 400 | 800 | 200 | 400 | 800 | CO2 | RH | CO2:RH | |
| Δ18OLW day (‰) | 9.9 (0.2) | 9.6 (0.5) | 8.6 (0.2) | 10.2 (0.9) | 9.2 (0.8) | 7.9 (0.4) | <0.01 | 0.55 | 0.47 |
| Δ18OLW night (‰) | 8.5 (0.3) | 8.2 (0.1) | 6.7 (0.4) | 8.8 (0.6) | 8.6 (0.1) | 7.6 (0.5) | <0.001 | 0.09 | 0.34 |
| Δ18OSSW (‰) | 18.7 (1.9) | 17.5 (0.7) | 15.9 (0.8) | 12.4 (0.5) | 11.3 (1.0) | 10.3 (0.2) | 0.02 | <0.001 | 0.74 |
| Δ18Oe (‰) | 18.0 (0.2) | 19.0 (0.1) | 20.1 (0.2) | 10.6 (0.4) | 12.3 (0.3) | 13.4 (0.1) | <0.001 | <0.001 | 0.19 |
| φLW | 0.45 (0.01) | 0.50 (0.02) | 0.57 (0.01) | 0.03 (0.11) | 0.26 (0.06) | 0.41 (0.03) | <0.001 | <0.001 | 0.03 |
| φSSW | −0.04 (0.12) | 0.08 (0.04) | 0.20 (0.05) | −0.17 (0.05) | 0.08 (0.06) | 0.23 (0.01) | <0.001 | 0.54 | 0.26 |
| Eleaf (mmol m−2 s−1) | 3.3 (0.3) | 2.3 (0.2) | 1.4 (0.1) | 2.9 (0.2) | 1.9 (0.2) | 1.0 (0.1) | <0.001 | 0.01 | 0.64 |
| (mol m−2 s−1) | 0.30 (0.03) | 0.19 (0.02) | 0.11 (0.01) | 0.78 (0.08) | 0.35 (0.04) | 0.16 (0.03) | <0.001 | <0.001 | <0.001 |
| gm (mol m−2 s−1) | 0.43 (0.04) | 0.37 (0.07) | 0.22 (0.05) | 0.36 (0.02) | 0.31 (0.03) | 0.14 (0.02) | <0.001 | 0.06 | 0.81 |
| LWC (mol m−2) | 12.2 (0.1) | 12.9 (0.2) | 13.8 (0.2) | 12.8 (0.0) | 12.2 (0.1) | 12.4 (0.0) | <0.01 | <0.01 | <0.001 |
| Turnover time (min) | 62 (1) | 92 (1) | 163 (2) | 73 (0) | 107 (1) | 212 (1) | <0.001 | <0.001 | <0.001 |
- Note: Averages for each treatment (mean ± SE) and p values of a two-way ANOVA for multiple physiological parameters measured in replicated mesocosm experiments. Significant effects are given in bold type. Averages were calculated based on individual leaf replicates in the case of gas exchange parameters (Eleaf, and gm, n = 6–12) and canopy scale replicates for all other parameters (n = 3–5).
- Abbreviations: ANOVA, analysis of variance; LW, leaf water; LWC, leaf water content; RH, relative humidity; SSW, sucrose synthesis water.
The 18O enrichment of photosynthetic medium water (Δ18OSSW) was calculated as Δ18OSucrose − εbio (with εbio constant at 26.7‰; see Section 2.7). Δ18OSucrose did not differ between samples collected between the end of the light and end of the dark period (Supporting Information: Table S1). Δ18OSSW responded to both RH and [CO2] treatments, with no significant interaction between RH and [CO2] (Table 2, Supporting Information: Figure S2). That is, the RH response was the same for all CO2 treatments. In all treatments, Δ18OSSW was more enriched than Δ18OLW, and this enrichment was much greater at low RH (+7.4 to +8.7‰) than at high RH (+2.2 to +2.4‰). At the same time, Δ18OSSW decreased by ∼2.4‰ between 200 and 800 μmol mol−1 CO2. The average RH and [CO2] sensitivities of Δ18OSSW were –0.24‰/% and –0.004‰/μmol mol−1.
Craig–Gordon modelled evaporative site enrichment (Δ18Oe) also responded significantly to RH and [CO2] (Table 2). However, the [CO2] effect on Δ18Oe was opposite to that for Δ18OSSW, as Δ18Oe increased (by 2.1‰ at low RH and 2.8‰ at high RH) when [CO2] during growth was increased from 200 to 800 μmol mol−1. The average RH and CO2 sensitivities of Δ18Oe were −0.28‰/% and +0.004‰/μmol mol−1.
Δ18OSSW was significantly related to Δ18Oe (R2 = 0.69, p = 0.04), but not to Δ18OLW (R2 = 0.20, p = 0.38) if all treatments were pooled (Figure 2). Nevertheless, there were treatment-specific differences between Δ18OSSW and Δ18Oe. While Δ18OSSW was similar to Δ18Oe at ambient [CO2], Δ18OSSW was higher than Δ18Oe at low [CO2] and lower at high [CO2]. This [CO2] effect on Δ18OSSW−Δ18Oe was very similar in the two RH treatments (Figure 2b).
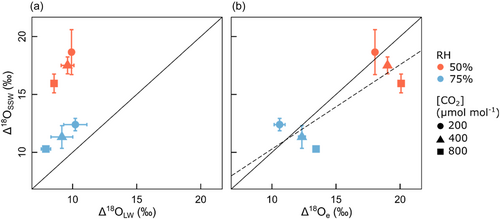
The proportional difference between Δ18OLW and Δ18Oe (φLW = 1 − Δ18OLW/Δ18Oe) varied between 0.03 and 0.57, and was influenced by RH and [CO2], as well as their interaction (Table 2). φLW was higher at low RH than at high RH at every [CO2] and increased with [CO2], with this [CO2]-driven effect being much higher at high RH. Conversely, the proportional difference between photosynthetic tissue water and evaporative site 18O enrichment (φSSW) was smaller (–0.17 to 0.23) and did not respond to RH, but increasing [CO2] caused an increase of φSSW.
3.2 Gas exchange parameters, LWC and turnover
Leaf measurements of stomatal conductance for water vapour () and transpiration (Eleaf) of paired plants were performed under conditions approximating those in the growth environment in each experimental run (Table 2) and have been reported by Baca Cabrera et al. (2020). Briefly, responded significantly to [CO2] and RH and their interaction. Specifically, decreased exponentially with [CO2] with an RH-sensitivity that decreased with [CO2]. In the low [CO2] treatment, was 2.6-fold greater at high than at low RH, but only 1.5-fold greater at high [CO2]). Eleaf also decreased exponentially (by ∼62%) with increasing [CO2] and was higher at low than at high RH (+12%, +22% and +45% at low, ambient and high [CO2]). Notably, the to Eleaf ratio decreased with [CO2]. This effect was (at least partially) related to systematic differences in air temperature among treatments (up to 1.3°C), caused by differences in Eleaf (leaf temperature was fixed at 21°C), associated offsets between leaf and air temperature (up to 0.9°C) (Figure 3) and offsets of actual relative to nominal %RH conditions (up to 3% RH) during gas exchange measurements in the leaf cuvette. We also observed systematic differences among treatments in the average canopy temperature (as measured with thermocouples; range 19.1–21.0°C), which were inversely related to canopy scale transpiration (Baca Cabrera et al., 2020). This indicates that the results observed at the leaf cuvette level were essentially also reflected at the entire sward scale.
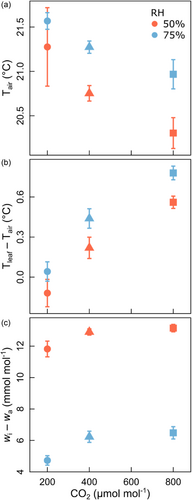
Mesophyll conductance (gm) decreased near-linearly by ~54% between low and high [CO2] and was ~26% smaller at high than at low RH (Table 2). Also, gm correlated linearly with Eleaf (R2 = 0.89), but the correlation between gm and gs was not significant.
LWC was practically the same in the different treatments (12.2–12.9 mol m−2), except at high [CO2]/low RH, where LWC was 11% higher than the average of the other treatments (Table 2). Accordingly, the turnover time of bulk leaf water (calculated as LWC/Eleaf) was primarily determined by the variation of Eleaf and varied between 62 min (low [CO2] and low RH) and 212 min (high [CO2] and high RH).
3.3 18O enrichment of nonphotosynthetic tissue water
18O enrichment of the nonphotosynthetic leaf water fraction (Δ18Onon-SSW) was first estimated by Equation 15 using a fnon-SSW = 0.53, the anatomically based estimate of the nonmesophyll water fraction in the bulk leaf (Figure 4a, left panel). The proportional offset of Δ18Onon-SSW from Δ18Oe (φnon-SSW = 1 − Δ18Onon-SSW/Δ18Oe) is given in Figure 4b (left panel). The estimates of Δ18Onon-SSW thus obtained relied on the assumption that the mesophyll was well-mixed (as explained in Section 2.7, and consistent with Equation 7), which implied that Δ18OSSW was representative for the entire mesophyll, including the mesophyll vacuoles. Under this assumption, Δ18Onon-SSW was 2.0‰ on average for the low RH treatments, implying that the δ18O of water in the non-SSW fraction was relatively close to source water (specifically, decreasing fnon-SSW below 0.48 predicted negative Δ18Onon-SSW for these treatments). Conversely, at high RH, isotopic mass balance (Equation 15) indicated that the nonphotosynthetic leaf water fraction was distinctly 18O enriched, and particularly so at low [CO2] (+8.3‰).
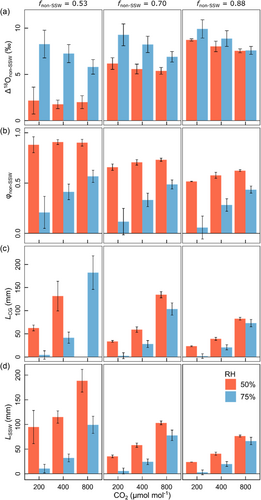
Increasing fnon-SSW from 0.53 to 0.88—which considered nonperfect mixing of the mesophyll, that is, an increasing proportion of the mesophyll having the same Δ18O as the nonmesophyll tissue—predicted increases of Δ18Onon-SSW (Figure 4a) and corresponding decreases of φnon-SSW in all treatments (Figure 4b). This effect was most apparent at low RH. That is, with the type of sensitivity analysis used here, consideration of nonperfect mixing of the mesophyll was associated with a much smaller effect on estimates of Δ18Onon-SSW at low RH than at high RH.
3.4 Relationships between gas exchange parameters and 18O enrichment of whole-leaf water, and of the photosynthetic and nonphotosynthetic tissue water fractions
Overall, the relationship between Eleaf and φLW was nonsignificant (R2 = 0.14; p > 0.05) and exhibited great scatter (Figure 5a). However, this scatter hid systematic, but opposing RH and [CO2] effects on the relationship between Eleaf and φLW: an RH-driven positive relationship evident at each individual [CO2] level, and a counteracting negative relationship driven by variation of [CO2], which was present at both RH levels. Meanwhile, Eleaf and φSSW (calculated as φSSW = 1 − Δ18OSSW/Δ18Oe) correlated negatively across the treatments (R2 = 0.81; p < 0.05) (Figure 5b). Conversely, the relationship between Eleaf and φnon-SSW (calculated as φSSW = 1 − Δ18Onon-SSW/Δ18Oe) was nonsignificant irrespective of the value at which fnon-SSW was fixed (Figure 5c for fnon-SSW = 0.53; data for other values of fnon-SSW not shown). Also, φnon-SSW displayed qualitatively similar treatment-dependent relationships with Eleaf as φLW (compare Figure 5a,c).
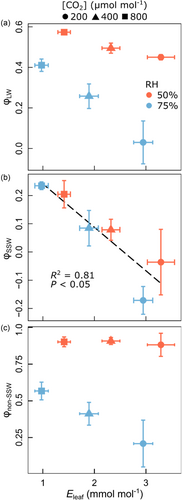
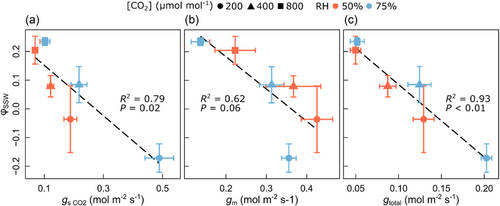
φSSW was negatively correlated with , gm and total conductance (gtotal, calculated as 1/(1/ + 1/gm) (Figure 6). The correlation between φSSW and gtotal was particularly strong (R2 = 0.93; p < 0.01), while the one with alone (R2 = 0.79; p = 0.02) appeared to vary between RH levels. The correlation of φSSW with gm was only marginally significant (R2 = 0.62; p = 0.06). In contrast, φLW and φnon-SSW did not correlate with gm (not shown), similar to the relationships with Eleaf, which were also nonsignificant (compare with Figure 5a,c).
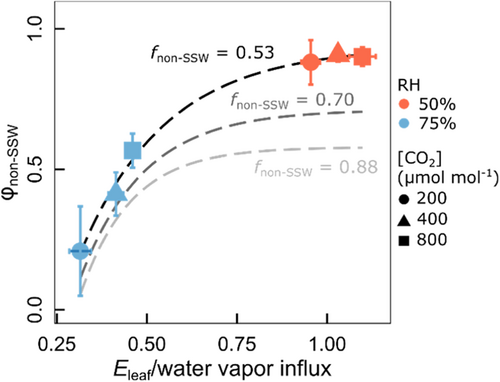
φnon-SSW demonstrated a very close, saturating relationship with the ratio of Eleaf to water vapour influx, estimated as × wa (Pseudo-R2 = 0.99, p < 0.05 for fixed fnon-SSW of 0.53) (Figure 7). Increasing fnon-SSW from 0.53 to 0.70 or 0.88 did not alter this relationship in a qualitative sense (Pseudo-R2 = 0.98 and 0.96, respectively), although it did change the value of the asymptote. Similar, although more blurred relationships existed between φLW and the ratio of Eleaf to water vapour influx (not shown). Conversely, there was no significant relationship (p > 0.05) between φSSW and the ratio of Eleaf to water vapour influx.
Using the data presented in Table 2 to fit the Péclet model as presented in Equation 7, we obtained estimates of the effective path length (termed LCG) for the different treatments (Figure 4c). These estimates of L were sensitive to (i) the assumptions of fnon-SSW used in the estimation of Δ18Onon-SSW, and growth conditions of (ii) [CO2] and (iii) daytime RH (Figure 4c). In general, however, L increased with increasing [CO2] and decreased with daytime RH. Specifically, at fnon-SSW = 0.53, L increased from 63 to 132 mm between low and ambient [CO2] (no value could be fitted for the high [CO2] level) at 50% RH and from 4 to 182 mm between high and low [CO2] at 75% RH. Alternatively, we also estimated L (termed LSSW, Figure 4d) using the same data, except for replacing Δ18Oe by Δ18OSSW, the Δ18O of the photosynthetic water pool, which is represented by the first term on the right-hand side of Equation 7. This yielded qualitatively similar estimates of L, except that the effect of [CO2] on L was attenuated. Thus, estimates of LSSW were higher than LCG at low [CO2], but lower at high [CO2].
4 DISCUSSION
4.1 On the approach—Advances and caution
Here, we present a new type of compartmental analysis of bulk leaf water 18O enrichment (Δ18OLW), based on the propositions of Holloway-Phillips et al. (2016) (see their eqns. 9–11). This analysis distinguished Δ18O in the photosynthetic tissue (Δ18OSSW) and nonphotosynthetic tissue (Δ18Onon-SSW) by using an isotopic mass balance (Equation 6) and estimates of the bulk leaf water fractions in photosynthetic and nonphotosynthetic leaf tissues, where the latter includes the veins and epidermis. This analysis rested partly, but significantly, on published comprehensive leaf anatomical analyses of C3 grasses (Dengler et al., 1994), including L. perenne (Charles-Edwards et al., 1974), the object of this work. This approach is functionally distinct and alternative to previous works which divided bulk leaf water into leaf lamina and primary vein water (see Section 1, Gan et al., 2002, 2003; Yakir et al., 1994) particularly for how water in the epidermis (a co-dominant component of bulk leaf water) is attributed to the functional parts of the leaf: exclusively associated with the nonphotosynthetic leaf tissue (which also includes the veins) in the present approach; and mostly with the lamina fraction (which includes the photosynthetic tissue) when the bulk leaf is separated in its lamina and (main) vein parts, in the earlier approach. Likewise, consistent with the proposition of Holloway-Phillips et al. (2016), we argue that the photosynthetic tissue was in (or near) equilibrium with 18O-enrichment at the evaporative sites as predicted by the Craig–Gordon model (although small offsets were systematic; see discussion under Section 4.2). Conversely, the nonphotosynthetic tissue, including vascular tissue and epidermis, appeared to display a treatment-dependent Péclet effect (Section 4.2).
However, the present analysis relied on several assumptions, including (1) that εbio for sucrose was the same (26.7‰) in all treatments, meaning that there was a constant offset between Δ18OSucrose and Δ18OSSW across treatments. Assumptions specifically important for the analysis of nonphotosynthetic tissue water fraction were more numerous and required, for all treatments, that (2) the mesophyll was well-mixed, (3) fnon-SSW was 0.53, (4) the ratio of assimilation to transpiration (A/E) was constant over the leaf surface and (5) that Equation 7, which was used to calculate L in the nonphotosynthetic tissue water fraction, provides a reasonable description of Δ18OLW. Considering uncertainty, however, we did relax specific assumptions of the analysis, as we discuss below.
Concerning (1): the temperature-dependent (Hirl et al., 2021; Sternberg & Ellsworth, 2011) εbio chosen here was very close to the ‘constant 27‰’ assumption which has been used most commonly (Barbour, 2007; Cernusak et al., 2005; Lehmann et al., 2017) as we used a thermal environment for which the εbio estimates of the two approaches converged closely (air temperature in the light period = 20°C). This estimate of εbio is taken from that for cellulose formation (Barbour, 2007; Cernusak et al., 2003); we are not aware of independent confirmations of εbio for sucrose in photosynthesizing leaves. Importantly, however, we found no evidence for incomplete equilibration of carbonyl groups with sucrose synthesis water, as the δ18O of sucrose did not differ significantly between plants grown in the presence of 18O-enriched or 18O-depleted CO2 (Supporting Information: Figure S3), similarly to cellulose (Liu et al., 2016). Also, the δ18O of bulk leaf water was not affected by the 18O of CO2 (p = 0.7).
Further, (2): Δ18OSucrose did not vary between the end of the light period and the end of the dark period, indicating that diurnal variation in mobilization of sucrose from the vacuole or recycling of sucrose via hydrolysis or fructan metabolism (Lattanzi et al., 2012; Pollock & Cairns, 1991) did not alter the 18O composition of sucrose. The apparent constancy of Δ18OSucrose could be related to a relative constancy of Δ18O of mesophyll water, as we observed only very small (if any) variation of Δ18OLW between the end of the day and end of the night. Conversely, however, Lehmann et al. (2017) found that hexoses were depleted by ∼2‰ relative to sucrose, equivalent to a ∼2‰ depletion of the synthesis water of hexoses relative to sucrose, if the εbio was the same for both sugars. This could indicate that metabolism of hexoses derived from sucrose was associated with significant oxygen exchange in a less 18O-enriched environment locally, or that the hexose-to-sucrose ratio varied along the leaf in parallel with 18O enrichment of medium water (Lehmann et al., 2017). Evidence for a different subcellular localization was presented by Wagner et al. (1983) who found hexoses to be virtually exclusively localized in the vacuole and a significant fraction of the sucrose in the cytosol of mesophyll cells isolated from barley primary leaves. Most interestingly, Koroleva et al. (1998) found a much higher hexose-to-sucrose ratio in epidermal cells of barley leaves than in the mesophyll (or bundle sheath parenchyma). If epidermis water is less 18O enriched than mesophyll water (as we suggest), this could also explain a lesser 18O enrichment of hexoses in whole-leaf extracts.
Nevertheless, we realize that direct empirical proof for the (eventual) constancy (or absence thereof) of εbio for leaf sucrose (εbio Sucrose) is presently missing. Certainly, there is a critical need for experimental determinations across a range of plant functional groups, environmental conditions and diurnal cycles (Holloway–Phillips et al. 2022). This includes possible metabolically based variation of εbio Sucrose (a) at the site of primary synthesis in the mesophyll, (b) during transport to and into sieve elements, and (c) in association with sucrose-consumption and resynthesis during eventual storage along the path in nonphotosynthetic leaf tissue.
Although we did not perform anatomical investigations ourselves, we believe that assumption (3) was well-founded for a fnon-SSW = 0.53, if the mesophyll was well-mixed. Estimates of mesophyll and nonmesophyll proportions of C3 grass leaves are known to vary comparatively little among and within studies (e.g., Charles-Edwards et al., 1974; Dengler et al., 1994; Garnier & Laurent, 1994; Winter et al., 1993). In particular, fractions of mesophyll and nonmesophyll tissue observed by Charles-Edwards et al. (1974) were remarkably constant among genotypes of L. perenne across contrasting growth conditions. Although leaf thickness correlated with the proportion of mesophyll, this parameter displayed little variation across diverse environments (Charles-Edwards et al., 1974). Also, we found very little variation of leaf thickness, based on LWC (Table 2). Moreover, leaf length and width, and epidermal cell number and length did not differ between treatments (Baca Cabrera et al., 2020). Finally, a minimum fnon-SSW ~ 0.5 was also supported by isotopic mass balance (Equation 15). Thus, we propose as the most parsimonious hypothesis that the proportions of mesophyll (and nonmesophyll) tissue, and hence fSSW (and fnon-SSW) were very closely similar between the different growth environments.
Assumption (4) is predicted by optimal stomatal control theory (Cowan & Farquhar, 1977) and supported by the close agreement between Δ18Oe and Δ18OSSW for the ambient [CO2] treatments at both high and low RH. Yet, we did observe small but systematic [CO2]-dependent variation of φSSW (range –0.17 to +0.23), as we discuss below.
4.2 18O enrichment of sucrose more closely related to evaporative site enrichment than to whole-leaf water
Our work confirms the observation of Lehmann et al. (2017) of a significant and RH-dependent underestimation of Δ18OSucrose by Δ18OLW + εbio (26.7‰) in L. perenne. In fact, the underestimation observed at low daytime RH was higher than that observed by Lehmann et al. (2017). Thus, the RH sensitivity of Δ18OSucrose (−0.24‰/%) was markedly greater at every [CO2] level than the RH sensitivity estimated for their data (ca. −0.16‰/% on average of the two grasses).
Additionally, our data reveal an overall closer agreement of Δ18OSSW (i.e., Δ18OSucrose − εbio) with Δ18Oe than with Δ18OLW. This result differs from the conclusion of Cernusak et al. (2003) which was based on the comparison of the 18O enrichment of phloem dry matter (mostly sucrose; e.g., Smith & Milburn, 1980) with lamina water (which excluded the main veins) or Δ18Oe in a dicot (R. communis). However, as our analysis was based on bulk leaf water, it is not strictly comparable with that of Cernusak et al. (2003). As shown by Gan et al. (2003) and Barbour et al. (2021), accounting for the vein fraction—which represents by itself only a fraction of the total nonphotosynthetic tissue water (see above)—already reduces substantially the discrepancy between 18O enrichment of lamina water and Δ18Oe. Unfortunately, sufficiently-rapid, artifact-free physical separation of the nonphotosynthetic and photosynthetic leaf tissue of L. perenne (or other C3 grasses) appears to be practically impossible at present (see also discussions in Cernusak et al., 2003).
The offset between Δ18OSSW and Δ18Oe was influenced strongly by [CO2], but not by RH or the interaction of [CO2] and RH. This effect correlated closely with the effect of [CO2] on Eleaf, gs, gm and gtotal. To our best knowledge, the relationship between φSSW and gas exchange parameters has not been investigated previously, reducing opportunities for discussion. However, Ferrio et al. (2012) observed an apparent coordination between mesophyll (and hydraulic) conductance and effective path length (L) in vein-severing experiments with droughted and control plants of Vitis vinifera. Our observation of a negative relationship between Eleaf and φSSW (Figure 5b) also implies a (strong) decrease of L with increasing Eleaf, an effect previously observed in tree species (Loucos et al., 2015; Song et al., 2013); and—since Eleaf and gm (as well as gtotal) were closely correlated—there may have also been a negative association between gm and L, consistent with observations of Ferrio et al. (2012), when applied only to photosynthetic medium water in the present case.
An increase in L under increasing [CO2] for both RH levels could also be related to changes in anatomical features of stomata. Studies in Arabidopsis (Larcher et al., 2015) and mangrove plants (Sternberg & Manganiello, 2014) indicated a decrease in L with increasing stomatal density, associated with a decrease in the distance between the stomatal pores and the veins and an increase in the total cross-sectional area through which mesophyll water flows. As [CO2] has risen, stomatal density has decreased (and pore size increased) over geological time (Franks & Beerling, 2009). A similar behaviour has been observed in controlled experiments under elevated [CO2] for a wide variety of species and accessions of Arabidopsis thaliana (Hetherington & Woodward, 2003). However, metaanalyses of FACE experiments indicate a weaker relationship between [CO2] and stomatal density, with low consistency (Ainsworth & Rogers, 2007; Poorter et al., 2022). We did not measure stomatal density or pore size in our experiment, but the observed positive relationship between [CO2] and L could be indicating a stomatal density-driven effect (i.e., increase in L with increasing CO2, due to lower stomatal density). Certainly, disentangling the effect of stomatal density/pore size and stomatal aperture (gas exchange) on L under rising [CO2] should be a target for future research.
Notably, based on our analysis, Δ18OSSW was slightly greater than Δ18Oe (implying that φSSW < 0) at low [CO2] in both RH treatments. As Δ18OSSW has not been analyzed previously, there is no other work with which this observation can be compared. However, negative values of φLW have been observed quite frequently in different plant functional groups (Cernusak et al., 2016, 2022), including in grasses (Helliker & Ehleringer, 2000), although such relationships are theoretically unexpected in steady-state conditions (Farquhar & Gan, 2003; Gan et al., 2003; Ogée et al., 2007). Because of the expectation that Δ18OSSW should always be greater than Δ18OLW, we would assume that such reported negative φLW values were also associated with (even more) negative φSSW values.
Errors in the simplifying assumptions for the calculation of Δ18Oe (i.e., absence of cuticular transpiration, stomatal patchiness and RH and temperature gradients between base and tip of the leaf and the canopy) could perhaps also contribute to a mismatch between Δ18Oe and Δ18OSSW. In particular, the increase in Δ18Oe from the leaf base toward the tip, which has been observed in grasses (Helliker & Ehleringer, 2000; Ogée et al., 2007) was not included in our model. A similar increase is expected for Δ18OSSW but has not been studied so far. At the same time, transpiration (E) (Helliker & Ehleringer, 2000; Ogée et al., 2007) and photosynthesis (A) (Meinzer & Saliendra 1997; Xiong et al., 2015) are known to increase from the leaf base to the leaf tip in grasses, and relative changes of the A/E ratio may vary along the leaf (Ocheltree et al., 2012), deviating from the constant A/E assumption. To which degree this relationship is affected by [CO2] has not been explored but could perhaps play a role in the spatial mismatch. Any spatial mismatch between (transpiration-weighted) Δ18Oe and (assimilation-weighted) Δ18OSSW, with weighted maximum assimilation occurring closer to the leaf tip than transpiration (Lehmann et al., 2017), could perhaps explain why Δ18OSSW > Δ18Oe or φSSW < 0 at low [CO2] (see also Ogée et al., 2007). In the same sense, the opposite spatial pattern could explain why Δ18OSSW < Δ18Oe or φSSW > 0 at high [CO2], that is, the weighted maximum assimilation occurring further away from the leaf tip than transpiration. Also, the [CO2]-dependent shifts could be connected to the fact that low [CO2] caused high gs and gm, while the opposite may have been the case at high [CO2]. Additionally, one may wonder, if a spatial mismatch between transpiration-weighted Δ18Oe and assimilation-weighted Δ18OSSW could also be associated with variation of transpiration and photosynthetic activity with depth inside the leaf. Finally, the assumption of a constant εbio discussed in Section 4.1 could also play a role in the discrepancy between Δ18Oe and Δ18OSSW at low and high [CO2]. Clearly, these are important questions for future investigations.
4.3 18O enrichment of nonphotosynthetic tissue water was sensitive to water vapour influx
Probably the greatest uncertainty in our analysis is connected with the estimation of Δ18Onon-SSW (and φnon-SSW) as this was determined from the residual of Equation 6 (hence integrated virtually all uncertainties discussed above, see Equations 15) and Equation 5 depended on the adequacy of Equation 7 for estimation of L. For the latter, we believe that the (variable) discrepancy between Δ18OSSW and Δ18OLW, the comparatively close relationship between Δ18OSSW and Δ18Oe, and the high φnon-SSW at low RH support well the model represented by Equation 7. Also, we did account for uncertainty in the assumption that the mesophyll was well mixed, by increasing the proportion fnon-SSW in a sensitivity analysis. All results demonstrated that estimates of L, and relationships of Δ18Onon-SSW and φnon-SSW with treatment effects and physiological parameters, remained the same in a qualitative sense.
In their analysis of the relative contributions of vapour and liquid water transport from the veins toward the stomata, Rockwell et al. (2014) predicted that an increase in Eleaf due to a decrease in ambient vapour mole fraction (wa) would pull the distribution of leaf internal evaporation away from the perivascular space toward the stomata. Such an effect should drive an increase of L (Barbour et al., 2017). This expectation is consistent with the RH effect on L of the non-SSW leaf water fraction as estimated here, either by Equation 7 (Figure 4c) or by using a modified Equation 7, in which Δ18Oe was replaced by Δ18OSSW in the first term on the right-hand side of the equation (Figure 4d). In both cases, the increase of L resulting from the decrease of RH in the growth environment was strong at every [CO2] level and for every fnon-SSW used in the estimation of Δ18Onon-SSW.
At the same time, L increased pronouncedly with increasing [CO2] in the growth environment. This effect was associated with a decrease in Eleaf, at both RH levels, independently of assumptions of fnon-SSW. Although Rockwell et al. (2014) did not explore effects of different [CO2] levels, this result is consistent with pulling the (evaporation-weighted) site of transpiration toward the periveinal/perivascular space when [CO2] is decreased. The leaf gas exchange measurements—performed under environmental conditions approximating those of the growth environment—indicated a very strong [CO2] effect on which entrained a parallel effect on Eleaf, the temperature gradient between leaf (TL) and air (Ta), TL − Ta, and hence wi − wa inside the leaf cuvette at both RH levels (Figure 3). Clearly, [CO2] must have had very strong effects on the energy balance of leaves, increasing the ratio of sensible to latent heat transfer, a situation that would cause an increase in the fraction of peristomatal evaporation (Rockwell et al., 2014). Again, this interpretation is consistent with our estimates of L increasing with [CO2]. The values of L (termed LCG) based on Equation 7 cover a wide range (2–182 mm for a fnon-SSW 0.53). The range of L estimated with Δ18Oe replaced by Δ18OSSW (termed LSSW) was distinctly smaller (by about half) but displayed qualitatively the same treatment response. Interestingly, the ranges of L estimated here are similar in magnitude to the ones obtained for whole leaves of another C3 grass (wheat) based on anatomical investigations and a range of scenarios concerning the site of evaporation within leaves (Barbour & Farquhar, 2004; Barbour et al., 2017).
An intriguing observation made here concerns the (saturating) relationship between φnon-SSW and the ratio of Eleaf to water vapour influx (Figure 7). An analogous asymptotic relationship was not observed for φSSW but existed also for φLW (Pseudo-R2 = 0.94), although the latter comprised more scatter due to the inclusion of the photosynthetic medium fraction in whole-leaf water. Eleaf equals source water influx into the leaf in the steady state, which very likely existed at the time of sampling (~14 h into the light period under constant environmental conditions, including irradiance). The ratio of Eleaf to water vapour influx abbreviates to (wi – wa)/wa when is eliminated from both the numerator and denominator of the ratio. This shows that at a given RH, variation of wi resulting from the variation of leaf temperature (controlled by ) was the main determinant of the variation of (wi – wa), as wa was kept near constant in the growth chambers. At high RH, the variation of wi drove a strong variation of φnon-SSW, with (wi – wa)/wa increasing dramatically in response to increasing [CO2] due to the increase of TL, which was a consequence of the gs-driven decrease in Eleaf. Thus, at high RH, variation of φnon-SSW appeared to be critically dependent on the energy balance of the leaf as controlled by . In that, it seems possible that the CO2-dependent relationship between (wi – wa)/wa and φnon-SSW is somehow connected with the position (depth inside the leaf) of evaporative sites, and related effects on L, particularly at high humidity.
4.4 Absence of a daytime RH effect on 18O enrichment of leaf water—Unreal, uncommon or just unnoted and underexplored?
Commonly, Δ18OLW exhibits a negative trend with RH (e.g., Cernusak et al., 2016, 2022; Helliker & Ehleringer, 2002; Hirl et al., 2019; Lehmann et al., 2017; Liu et al., 2017), a relation that we did not find here. But, we did find evidence of some effect of daytime evaporative conditions in bulk leaf water composition, based on the observations that the deuterium deviation with reference to the global meteoric water line (Voelker et al., 2014; Wei & Lee, 2019) was higher at low RH than at high RH, for all [CO2] levels (Figure 1, Supporting Information: Table S2).
The commonly expected relation between RH and Δ18OLW is generally interpreted in terms of predictions from the Craig–Gordon model (e.g., Roden & Ehleringer, 1999), which dictates a strong negative effect of increasing RH on Δ18Oe (Equation 1) and propagation of this enrichment in leaf water (Barbour, 2007; Cernusak et al., 2016, 2022; Craig & Gordon, 1965; Dongmann et al., 1974; Farquhar et al., 1989, 2007; Flanagan et al., 1991). However, a recent compilation of published and previously unpublished leaf water isotope data (data set S1 in Cernusak et al., 2022) demonstrates an (RH-insensitive) global average φLW of 0.16, which indicates that the RH sensitivity of Δ18OLW should be about 16% smaller than that of Δ18Oe. However, φLW can be much greater (Cernusak et al., 2016), which would further reduce the RH sensitivity of Δ18OLW in these cases. Specifically, the grassland (Hirl et al., 2019) and grass species (Stipa capillata, Zhao et al., 2014) included in the Cernusak et al. (2022) data set had an average φLW of 0.36 and 0.45, respectively, suggesting per se a 36% and 45% reduced RH sensitivity of Δ18OLW relative to Δ18Oe. Moreover, φLW exhibited a common negative RH response of −0.005%−1 in the studies of Hirl et al. (2019) and Zhao et al. (2014) (data collected between 10 AM and 4 PM), respectively (Supporting Information: Figure S4), a fact not highlighted or discussed before. This negative RH response of φLW implied an additional 13% reduction of the RH effect on Δ18OLW in the range from 50% to 75% RH. In the present work, we observed a mean φLW of 0.37 and an RH-sensitivity of φLW (−0.01%−1) which was twice that of Hirl et al. (2019) and Zhao et al. (2014). This greater negative RH response of φLW effectively cancelled the RH effect on Δ18OLW in our investigations and was mainly related to the opposite effects of RH on Δ18Onon-SSW relative to Δ18OSSW. Notably, other datasets with a nonsignificant RH response of Δ18OLW are also included in the data set of Cernusak et al. (2022) and comprise the S. capillata data of Zhao et al. (2014; samples collected between 10 AM and 4 PM and reflecting an RH range from 26% to 56%). Notably, the RH sensitivity of ∆18OLW which we calculate from the data of Lehmann et al. (2017) is also quite low, when compared to the average response of the global data set of Cernusak et al. (2022): −0.09‰/% versus −0.30‰/%. These findings and considerations all support the view that the magnitude and range of the φLW and ∆18OLW data and their response to RH, as observed in the present work, fall inside the range of observations made previously by others in diverse environments (Cernusak et al., 2022).
5 CONCLUSION AND OUTLOOK
This work demonstrated that Δ18OSSW was well predicted by Δ18Oe with offsets that correlated with gas exchange parameters (gs or total conductance to CO2) influenced by [CO2] in the growth environment. Offsets between Δ18OSSW and Δ18Oe may have resulted from spatial gradients of evaporative 18O enrichment in the mesophyll which diverged from spatial patterns of photosynthetic activity. Remarkably, Δ18OLW was a poor predictor of Δ18OSSW, as RH had an opposite effect on Δ18Onon-SSW relative to Δ18OSSW. The effect of Δ18Onon-SSW on Δ18OLW was strong, as the fraction of nonphotosynthetic tissue water in bulk leaf water was high, with epidermis water a dominant component. Leaf-to-air temperature gradients were mainly dependent on [CO2] and had a strong effect on φnon-SSW, a phenomenon that correlated with the transpiration-to-water vapour influx ratio, particularly at high RH. Based on the present analysis, we believe that future work should target the following questions: (1) Which constitutive biophysical mechanisms determine the variation of φSSW and its relationship with gs, gm and gtotal? (2) How do the opposite effects of CO2 and RH on the E vs L relationship affect the interpretation of Δ18OLW signals, especially in the case of long-term timeseries (climate change); (3) Is RH sensitivity of Δ18OLW influenced by leaf hydraulic design or energy balance? And how do these factors influence Δ18Onon-SSW in particular? And more generally; (4) which mechanisms underlie the natural variation of the RH sensitivity of Δ18OLW, beyond effects of nonsteady-state, vapour isotope composition or boundary-layer and stomatal conductance?
ACKNOWLEDGEMENTS
We thank Anja Schmidt, Monika Michler, Angela Ernst-Schwärzli, Laura Dorn, Wolfgang Feneis, Richard Wenzel and Hans Vogl for skillful assistance in sampling and sample processing (A. S., M. M., A. E. S., H. V.), carbohydrate analyses (A. S., L. D.), maintenance of the mesocosm facility and gas exchange equipment (W. F., R. W.), and manufacturing thermocouples for leaf temperature measurements (R. W.). We acknowledge preliminary discussions with Haitao Liu (Henan Agricultural University, China) and Xiaoying Gong (Fujian Normal University, China), as well as comments of Rolf Siegwolf (Eidg. Forschungsanstalt für Wald, Schnee und Landschaft, WSL, Switzerland). Comments of Guillaume Tcherkez and two anonymous referees helped us greatly to improve the paper. This research was supported by the Deutsche Forschungsgemeinschaft (DFG SCHN 557/9-1). J. Z. was supported by the China Scholarship Council (CSC). Open Access funding enabled and organized by Projekt DEAL.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest
Open Research
DATA AVAILABILITY STATEMENT
The data sets that support the findings of this study are available from the corresponding author on reasonable request.




