FTIR Spectroscopic and Theoretical Study of the Photochemistry of Matrix-isolated Coumarin
It must be noted here that the HOMA index has been only defined for molecules with C–C and C–N bonds (see Refs. [ 46–49]). That is why in our estimations of the HOMA index for the α-pyrone and the pyrone sub-unit of coumarin only the four CC bonds were used, i.e. the obtained values (0.475 and 0.526) are average values over these four bonds only.
Abstract
The infrared spectrum of monomeric unsubstituted coumarin (C9H6O2; 2H-1-benzopyran-2-one), isolated in solid argon at 10 K is presented and assigned. The UV-induced (λ > 200 nm) unimolecular photochemistry of the matrix-isolated compound was studied experimentally. Three main photoreactions were observed: (a) decarboxylation of the compound and formation of benzocyclobutadiene and CO2, with the Dewar form of coumarin as intermediate; (b) isomerization of the compound, leading to production of a conjugated ketene; and (c) decarbonylation, leading to formation of CO and benzofuran complex. Further decomposition of benzofuran to produce ethynol is suggested. Photochannels (a) and (b) correspond to those previously observed for matrix-isolated α-pyrone and its sulfur analogs (Phys. Chem. Chem. Phys. 2004, 6, 929; J. Phys. Chem. A 2006, 110, 6415), while route (c) is similar to the UV-induced photochemistry of coumarin in the gaseous phase (J. Phys. Chem. A 2000, 104, 1095). Interpretation of the experimental data is supported by extensive calculations performed at the B3LYP/6-311++G(d,p), MP2/6-31G(d,p) and MP2/6-311++G(d,p) levels.
Introduction
Coumarin is the name given to the basic structural unit present in a large group of heterocyclic oxygen compounds that possess the benzopyran-2-one nucleus. As early as in the mid-1930s, Späth and coworkers carried out an extensive study on the isolation and structural elucidation of a large number of coumarins from plants belonging to the Umbelliferae family (1–3). After Späth’s studies there was a comparative lull in the research of coumarins, until the 1960s, when there was a noticeable re-wakening of interest in naturally occurring coumarins. Because of its many practical applications, this family of compounds is nowadays the subject of intensive research (4).
Coumarins are widely used as dyes owing to their efficient light emission properties, high stability and easy synthesis (4–9). They are of considerable biological and medical interest, showing important physiological effects (anti-coagulant, anti-HIV, anti-tumor, anti-hypertension, anti-arrhythmia and anti-osteoporosis activities, weak toxicity, etc.) (10–14). Natural products like esculetin, fraxetin, daphnetin and other related coumarin derivatives are also recognized to possess anti-inflammatory as well as antioxidant activities (15,16). Coumarins are also currently used in perfumes and agrochemical production (17).
Very surprisingly, unsubstituted coumarin (2H-1-benzopyran-2-one; Fig. 1) has only been scarcely studied both from structural and spectroscopic points of view. The structure of coumarin has been solved for the crystalline compound and predicted theoretically using the semiempirical (AM1), Hartree-Fock (HF) and DFT/B3LYP methods [with the modest 4–31 G(O*) or 6-31G* basis sets] (18,19). Coumarin crystals were found to be orthorhombic (a = 15.4669, b = 5.66022, c = 7.7448 Å), space group Pca2(1), with four molecules per unit cell (19). The X-ray diffraction study at 90 K showed that weak C−H···O and C−H···π interactions stabilize the crystal lattice of coumarin (20). Variations in charge density properties and derived local energy densities were investigated in the regions of intermolecular interactions. Theoretical charge density calculations on crystals, using the B3LYP/6-31G** method, showed agreement with the experimentally obtained properties and energy densities (20). No experimental data on the gas phase structure of coumarin have been reported hitherto.
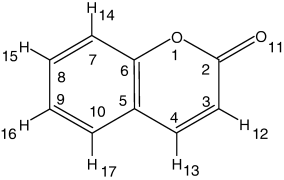
Molecular structure of coumarin, with adopted atom numbering. Note that the present atom numbering is different from the IUPAC recommendations, for the sake of easier comparison between coumarin and α-pyrone.
The infrared (IR) spectra of the compound in several solvents were obtained by Nyquist and Settineri (21) and predicted theoretically at the DFT/B3LYP/6-31G* level of theory by Hsieh et al. (19). Raman spectra of coumarin and several of its isotopologues in deoxygenated ethanol solution were obtained experimentally by Uesugi et al. (18), who also presented partial data (only in-plane vibrations in the 1750–280 cm−1 range) on the ab initio HF calculated spectra for these species. In the latter work, the radical anion as well as the lowest excited triplet state of coumarin were also studied using time-resolved resonance Raman spectroscopy. UV and NMR spectra of coumarin have also been reported previously (22,23). To the best of our knowledge, no experimental vibrational data for coumarin in the gas-phase or for the molecule isolated in cryogenic inert matrices have been reported.
In 1993, McCarthy and Blanchard (24) studied the electronic structures of a series of coumarin molecules using the AM1 method. They calculated the ground-state, first excited triplet state and first excited singlet state energies and dipole moments, as well as their dependence on the geometries and on different side groups. They demonstrated the complexity associated with the optical response of coumarins. Because of the multitude of electronic states in close energetic proximity to S1, and the propensity to intersystem crossing to their triplet manifold, it was concluded that coumarins as a class are less than ideal for probing transient photophysical and dynamical processes (24). A few years later, the electronic structure and other properties of 21 coumarin derivatives, including the nonsubstituted compound, were investigated by a combination of experimental and theoretical methods: UV photoelectron spectra, UV–visible spectroscopy and semi-empirical MO calculations (25,26). It was reported that the excited electronic states of coumarins that are responsible for their luminescent properties have high density in the vicinity of S1. It was pointed out that (in keeping with the high density of states in the vicinity of S1) the emission bands of coumarins are broad and featureless. Further, from the analysis of the intensity and band shape of the 0−0 transition, HOMO and HOMO−2 in coumarine were described as having bonding character, while in HOMO−1 and HOMO−3 the bonding character was suggested to be less pronounced (25).
The photophysical properties of coumarin have been quite extensively investigated both experimentally and theoretically (27–31). Experimentally, it was found that the first excited singlet state of coumarin showed an energy of 82 kcal mol−1 (28 680 cm−1) relative to the ground state (32). It was also shown that the S1 state is of nπ* character and stays well below the S2(ππ*) state, the difference in energy between these two states decreasing with solvent polarity (27). Very interestingly, in di- and tri-substituted coumarins the order of the nπ* and ππ* states may be inverted (27). The three lowest excited states of the triplet manifold were shown to have lower energies compared with the S1 state; the first two triplet states have ππ* character and the third one is nπ* (27,33). In a rigid matrix of ethanol ether at 77 K (33), the lowest energy triplet state gives rise to phosphorescence with a 0–0 band at 458 nm (21 830 cm−1). The experimental energies of S1 (32) and T1 (33) states are in a good agreement with the calculated values (27).
The photochemistry of coumarin has also been the subject of numerous studies. The photochemical dimerization of coumarin in solution is a well-known reaction in organic photochemistry since the early 1960s (see, for example, Ref. [34] and references therein). In nonpolar solvents such as benzene, the interaction of excited singlet coumarin with ground state coumarin leads only to self-quenching (32). In polar solvents such as ethanol, the interaction of excited singlet coumarin with ground state coumarin leads to both self-quenching and formation of the cis-head-to-head dimer. In the presence of triplet sensitizers such as benzophenone, the trans-head-to-head dimer is formed. In sensitized reactions, triplet coumarin is produced by energy transfer from the excited triplet sensitizer. On the other hand, in the direct reaction at high dilution, intersystem crossing in coumarin can compete with self-quenching and the trans-head-to-head dimer is produced without involving a sensitizer (32). It has been recently shown (35) that the cyclization reaction is a two-photon-induced process and that this process is photoreversible.
The irradiation of gaseous coumarin by an ArF excimer laser (λ = 193.3 nm) resulted in the decarbonylation of the compound, with benzofuran being the second photoproduct (36). The triplet state, fluorescence and cation radical of coumarin were not observed in the transient spectra. The addition of nitrogen effectively quenched the formation of benzofuran, indicating that this compound was obtained from a highly vibrationally excited state of coumarin. Moreover, it was concluded (36) that the vibrationally hot coumarin was an intermediate in the two-photon decarbonylation reaction. The ArF excimer laser irradiation induced a reaction similar to that observed in the flash vacuum pyrolysis at 1100 K (37).
In the present work, we focus attention on the photochemistry of monomeric coumarin isolated in low temperature inert matrices; to the best of our knowledge these data are reported for the first time. The structural and vibrational properties of matrix-isolated coumarin and a variety of its possible photoproducts are also investigated. Interpretation of the experimental data is supported by extensive DFT(B3LYP)/6-311++G(d,p), MP2/6-31G(d,p) and MP2/6-311++G(d,p) calculations.
Materials and Methods
Experimental details. Coumarin was obtained from Sigma (purity 99%). The IR spectra were obtained using a Mattson (Infinity 60AR Series) Fourier transform IR spectrometer, equipped with a deuterated triglycine sulfate detector and a KBr beamsplitter, with 0.5 cm−1 spectral resolution. Necessary modifications of the sample compartment of the spectrometer were made to accommodate the cryostat head and allow purging of the instrument by a stream of dry nitrogen to remove water vapor and CO2. A solid sample of coumarin was placed in a specially designed Knudsen cell with shut-off possibility, whose main component is a NUPRO SS-4BMRG needle valve (38). The cell was kept at a room temperature (24°C) during deposition of the sample. At this temperature, the saturated gas pressure over the solid coumarin was found to be sufficient to assure a reliable deposition, therefore the cell was not heated. In order to deposit a matrix, the vapor of coumarin was codeposited together with large excess of the host matrix gas (argon N60, from Air Liquide) onto a cold CsI window (T = 10 K) mounted on the tip of the cryostat. All experiments were performed on the basis of an APD Cryogenics closed cycle helium refrigeration system with a DE-202A expander. The matrices were irradiated using a series of long-pass optical filters, through the outer quartz window of the cryostat, using a 200 W output power of the 500 W Hg(Xe) lamp (Oriel, Newport). The lowest wavelength coming out of the lamp (200 nm) defined the upper limit of UV energies available for photochemical excitations.
Computational methodology. The equilibrium geometries for coumarin and its photoproducts were fully optimized at the DFT level of theory with the 6-311++G(d,p) split valence triple-ζ basis set, and using the ab initio MP2 method with the 6-31G(d,p) and 6-311++G(d,p) basis sets. The DFT calculations were carried out with the three-parameter B3LYP density functional, which includes Becke’s gradient exchange correction (39) and the Lee, Yang, Parr correlation functional (40). The MP2 calculations were found to provide better results, compared with the DFT approach, in the characterization of systems with nonbonded interactions. In the MP2 calculations, the potential energy surface of coumarin and its photoproducts was initially investigated at the MP2/6-31G(d,p) level. In selected cases, the MP2 calculations were also carried out at a higher theory level, MP2/6-311++G(d,p), in order to ensure that the structures of noncovalently bonded dimers (e.g. [benzofuran + CO]) do exhibit attractive profiles. Whenever possible, molecular symmetry (Cs point group) was conserved. All calculations were carried out using the GAUSSIAN 98 program (41).
Vibrational spectra were calculated at both the DFT(B3LYP)/6-311++G(d,p) and MP2/6-31G(d,p) levels of theory, using the built-in analytic standard algorithms of GAUSSIAN 98. Subsequent transformations of the Cartesian force constants to molecule-fixed symmetry adjusted internal coordinates allowed the ordinary normal-coordinate analysis to be performed as described by Schachtschneider (42). The symmetry internal coordinates used in this analysis were defined in the manner recommended by Pulay et al. (43), and are provided as Supplemental Materials to this article. Potential energy distribution (PED) matrices (44) have been calculated and the elements of these matrices greater than 10% were used to characterize the different vibrations in terms of the chosen symmetry coordinates. In order to correct for vibrational anharmonicity, basis set truncation and the neglected part of electron correlation, the calculated frequencies were scaled as specified below.
Results and discussion
Molecular structure and IR spectrum of coumarin
The DFT and MP2 calculated equilibrium geometries for coumarin are given in Table 1, where they are compared with the X-ray structure of the compound in the crystalline state (19). From the analysis of the two datasets (calculated vs experimental) it can be concluded that the calculated geometry for the monomer in vacuum is in excellent agreement with the X-ray data, indicating that, in the condensed phase, the intermolecular interactions introduce only relatively unimportant effects on the electron distribution in the coumarin molecules. It is worth noticing that this result follows the trend previously observed for both α- and γ-pyrone (45), where intermolecular interactions in the condensed phases were also found to affect the structure and vibrational properties of the molecules only very slightly.
| Coumarin | α-pyrone (45) | |||
|---|---|---|---|---|
| B3LYP 6-311++G(d,p) | MP2 6-31G(d,p) | Exp. X-ray (19) | B3LYP 6-311++G(d,p) | |
| Bond length (Å) | ||||
| O1−C2 | 1.396 | 1.396 | 1.374 | 1.419 |
| O1−C6 | 1.365 | 1.373 | 1.378 | 1.344 |
| C2−C3 | 1.459 | 1.461 | 1.454 | 1.450 |
| C=O | 1.202 | 1.215 | 1.213 | 1.201 |
| C3=C4 | 1.349 | 1.353 | 1.347 | 1.357 |
| C3−H12 | 1.082 | 1.080 | 1.082 | |
| C4−C5 | 1.440 | 1.441 | 1.438 | 1.431 |
| C4−H13 | 1.086 | 1.084 | 1.085 | |
| C5−C6 | 1.405 | 1.404 | 1.397 | 1.350 |
| C5−C10 | 1.406 | 1.406 | 1.405 | |
| C6−C7 | 1.394 | 1.396 | 1.394 | |
| C7−C8 | 1.389 | 1.390 | 1.383 | |
| C7−H14 | 1.083 | 1.082 | ||
| C8−C9 | 1.402 | 1.403 | 1.397 | |
| C8−H15 | 1.084 | 1.082 | ||
| C9−C10 | 1.385 | 1.388 | 1.380 | |
| C9−H16 | 1.083 | 1.082 | ||
| C10−H17 | 1.085 | 1.084 | ||
| Bond angle (degrees) | ||||
| C2−O1−C6 | 122.9 | 122.1 | 121.9 | 122.4 |
| O1−C2−C3 | 115.9 | 116.2 | 117.4 | 114.7 |
| O1−C=O | 117.9 | 118.2 | 116.8 | |
| C2−C3=C4 | 121.7 | 122.0 | 121.4 | 121.5 |
| C4=C3−H12 | 122.8 | 122.5 | 122.6 | |
| C3=C4−C5 | 120.8 | 120.3 | 120.1 | 120.5 |
| C5−C4−H13 | 118.7 | 119.1 | 119.5 | |
| C4−C5−C6 | 117.4 | 117.6 | 118.1 | 117.8 |
| C4−C5−C10 | 124.1 | 123.9 | 123.6 | |
| O1−C6−C5 | 121.3 | 121.8 | 121.1 | 123.0 |
| O1−C6−C7 | 117.5 | 116.7 | 116.9 | |
| C6−C7−C8 | 119.0 | 119.0 | 118.4 | |
| C6−C7−H14 | 119.1 | 118.9 | ||
| C7−C8−C9 | 120.8 | 120.6 | 120.9 | |
| C7−C8−H15 | 119.4 | 119.5 | ||
| C8−C9−C10 | 119.8 | 120.0 | 120.3 | |
| C8−C9−H16 | 120.0 | 119.9 | ||
| C5−C10−C9 | 120.6 | 120.4 | 120.2 | |
| C5−C10−H17 | 118.9 | 118.9 | ||
- *Dihedral angles are not shown in the table as both molecules (coumarin and α-pyrone) are planar species.
Table 1 also shows the equilibrium geometry calculated for α-pyrone (45) at the DFT(B3LYP)/6-311++G(d,p) level of theory. Comparison of the structural parameters obtained for the two molecules at the same level of theory (in particular, bond lengths) allowed us to shed light on the influence of the phenyl ring of coumarin on the electronic properties of its pyrone ring.
The C6=C5 bond length increases considerably upon going from α-pyrone to coumarin (from 1.350 to 1.405 Å), which is a consequence of the involvement of this bond in the π-delocalization associated with the phenyl ring of coumarin (see structure II in Scheme 1).
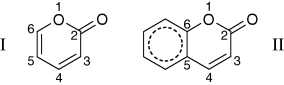
Comparative scheme of structures of α-pyrone (I) and coumarin (II).
In coumarin, the C2−O1 and C3=C4 bonds are shorter than in α-pyrone, while the C6−O1, C4−C5 and C2−C3 bonds are longer; moreover, the calculated carbonyl bond lengths are approximately equal in coumarin and α-pyrone. These trends can be explained as follows: in α-pyrone the C3=C4−C5=C6 fragment is linearly conjugated, which results in a delocalization of the ring π-electrons over these four carbon atoms (and also somewhat over the C=O bond). On the other hand, in coumarin, as mentioned above, C5 and C6 atoms share their π-electron densities with the benzene sub-unit, which becomes almost ideally aromatic (structure II in Scheme 1). Then, in this molecule, C5 and C6 are not contributing their π-electrons to share with the C3 and C4 atoms of the pyrone sub-unit and, consequently, the C3=C4 bond gains a stronger double-bond character compared with the equivalent bond in α-pyrone, while the adjacent CC bonds turn more pronounced as single bonds (i.e. C4−C5 and C2−C3 bonds become longer). Furthermore, because of the weakening of the C2−C3 bond, the adjacent C2−O1 becomes shorter in coumarin. This trend is reinforced because the C6−O1 bond (adjacent to the C2−O1 bond) is weakened by its interaction with the aromatic benzene sub-unit. In consonance with the similar calculated values for the carbonyl bond in the two molecules, one may conclude that the electronic density of the carbonyl group is practically not affected by the presence of the additional phenyl ring in coumarin.
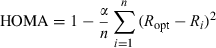
We estimated the HOMA index for α-pyrone and each ring of coumarin using the bond lengths calculated at the MP2/6-31G(d,p) level of theory. The reference value Ropt was taken equal to 1.3963 Å, which corresponds to the CC bond length in the molecule of benzene optimized at the MP2/6-31G(d,p) theory level. The value of 0.987 was obtained for the benzene sub-unit of coumarin, which indicates that this ring shows an appreciable aromatic character. For the pyrone sub-unit of coumarin, HOMA = 0.475, while for α-pyrone HOMA =0.526, i.e. there is indeed a decrease in the level of π-electron delocalization in the pyrone ring when the phenyl ring is attached to it.1
The IR spectrum of monomeric coumarin isolated in an argon matrix (T = 10 K) is presented in Fig. 2, together with the DFT(B3LYP)/6-311++G(d,p) and MP2/6-31G(d,p) calculated spectra. The calculated data facilitated the assignment of the observed spectrum, which is given in Table 2. Tables S1–S3, provided as Supplemental Materials, summarize the results of the normal coordinates analysis, which was undertaken based on both the calculated DFT and MP2 force constants and optimized geometries. Table S1 contains the definition of the symmetry coordinates used in these calculations, whereas Tables S2 and S3 give the calculated PEDs.
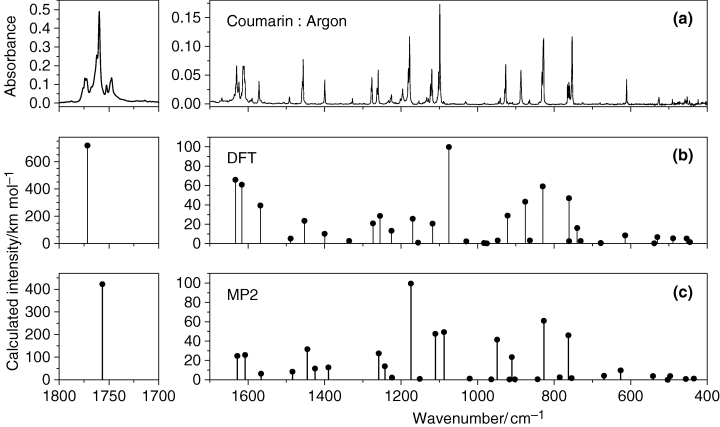
(a) Experimental FTIR spectrum of coumarin isolated in an argon matrix (T = 10 K). (b) Spectrum of coumarin monomer calculated at the B3LYP/6-311++G(d,p) level of theory. The calculated wavenumbers were scaled with a factor of 0.982 in the 2500–1000 cm−1 range and with a factor of 0.989 in the range below 1000 cm−1. (c) Spectrum of coumarin monomer calculated at the MP2/6-31G(d,p) level of theory. The calculated wavenumbers were scaled with a factor of 0.956 in the 2500–1000 cm−1 range and with a factor of 1.014 in the range below 1000 cm−1.
| Approximate description† | Symmetry | Calculated DFT(B3LYP)/6-311++G(d,p) | Calculated MP2/6-31G(d,p) | Observed spectra Ar (10 K) | |||
|---|---|---|---|---|---|---|---|
| Frequency‡ | Intensity | Frequency§ | Intensity | Frequency | Intensity|| | ||
| ν(C3−H) | A′ | 3099 | 0.3 | 3100 | 0.5 | – | |
| ν(C7−H) | A′ | 3088 | 3.2 | 3087 | 4.1 | 3096 | 1.0 |
| ν(C9−H) | A′ | 3079 | 11.0 | 3079 | 10.6 | 3085, 3079 | 1.5 |
| ν(C8−H) | A′ | 3065 | 7.0 | 3064 | 5.5 | 3059 | 1.0 |
| ν(C10−H) | A′ | 3055 | 5.2 | 3050 | 0.9 | 3053 | 1.1 |
| ν(C4−H) | A′ | 3051 | 4.1 | 3052 | 11.0 | 3043 | 0.7 |
| ν(C=O) | A′ | 1772 | 718.0 | 1757 | 422.3 | 1776, 1774, 1772, 1767, 1762, 1759, 1752, 1748, 1747 | 456.6 |
| ν(C3=C4) | A′ | 1633 | 65.9 | 1628 | 24.8 | 1635, 1632, 1631, 1630 | 45.0 |
| ν(C10−C9) | A′ | 1616 | 60.7 | 1608 | 25.7 | 1617, 1613, 1612, 1610 | 54.1 |
| ν(C8−C7) | A′ | 1568 | 39.3 | 1566 | 6.3 | 1572, 1571 | 12.7 |
| δ(C−H) ph | A′ | 1489 | 5.2 | 1484 | 8.4 | 1492 | 3.2 |
| ν(C7−C6) | A′ | 1453 | 23.4 | 1445 | 31.6 | 1459, 1458, 1455 | 25.8 |
| δ(C−H) py | A′ | 1400 | 10.1 | 1425 | 11.6 | 1399 | 9.8 |
| ν(C5−C6)/δ(C−H) ph | A′ | 1336 | 2.7 | 1390 | 12.8 | 1329, 1327 | 1.9 |
| δ(C−H) ph/ν(C5−C6) | A′ | 1273 | 20.7 | 1258 | 27.3 | 1278, 1276, 1275 | 13.2 |
| ν(C6−O) | A′ | 1255 | 28.6 | 1242 | 14.0 | 1263, 1262, 1260, 1259 | 17.6 |
| ν(C4−C5) | A′ | 1225 | 13.1 | 1224 | 2.2 | 1233, 1232, 1228, 1226, 1225 | 13.8 |
| δ(C−H) py/ν(C2−C3) | A′ | 1169 | 25.6 | 1174 | 99.5 | 1202, 1197, 1196, 1194, 1181, 1178 | 69.2 |
| δ(C−H) ph | A′ | 1156 | 0.9 | 1151 | 0.9 | 1156, 1153 | 1.2 |
| δ(C−H) ph | A′ | 1118 | 20.5 | 1111 | 47.5 | 1134, 1132, 1129, 1128, 1123, 1119, 1118 | 32.6 |
| ν(C2−C3)/δ(C−H) py | A′ | 1075 | 99.8 | 1088 | 49.2 | 1106, 1102, 1098, 1097 | 56.1 |
| ν(C9−C8) | A′ | 1030 | 2.2 | 1021 | 1.3 | 1031, 1030 | 1.0 |
| γ(C−H) py | A′ | 983 | 0.5 | 964 | 0.5 | 984, 982 | 0.2 |
| γ(C−H) ph | A′ | 969 | 0.2 | 917 | 0.3 | – | |
| γ(C−H) ph | A′ | 948 | 3.2 | 903 | 0.5 | 945, 944, 942, 940 | 3.4 |
| ν(O−C2)/δ ring ph | A′ | 922 | 28.8 | 911 | 23.5 | 929, 927, 926 | 19.8 |
| δ ring ph/ν(O−C2) | A′ | 875 | 43.3 | 949 | 41.5 | 888, 886 | 21.0 |
| γ(C−H) ph | A′ | 863 | 3.1 | 843 | 0.6 | 866, 865, 864 | 2.3 |
| γ(C−H) py | A′ | 830 | 59.1 | 827 | 61.0 | 832, 829, 828, 827 | 52.2 |
| ν(C10−C5) | A′ | 761 | 2.5 | 785 | 2.6 | 765, 763, 762, 761, 759, 753 | 56.2 |
| γ(C−H) ph | A′ | 761 | 46.8 | 763 | 46.0 | ||
| τ ring py¶ | A′ | 740 | 15.9 | ||||
| δ ring ph | A′ | 731 | 2.6 | 754 | 1.7 | 726, 725 | 1.1 |
| γ(C=O) | A′ | 678 | 0.5 | 669 | 4.2 | 680 | 0.2 |
| δ ring py | A′ | 614 | 8.3 | 626 | 9.7 | 610 | 7.3 |
| τ ring py | A′ | 538 | 0.2 | 503 | 0.0 | – | |
| δ ring py | A′ | 530 | 6.7 | 542 | 3.9 | 527, 526 | 2.0 |
| δ(C=O) | A′ | 489 | 5.4 | 497 | 3.9 | 490, 486(?) | 0.6 |
| τ Butterfly | A′ | 454 | 5.2 | 435 | 1.3 | 459, 452 | 4.6 |
| δ ring ph | A′ | 445 | 1.5 | 456 | 0.8 | 446 | 0.3 |
| τ ring py¶ | A′ | 355 | 0.4 | ||||
| τ ring ph | A′ | 369 | 0.1 | 327 | 0.1 | ||
| δ ring py | A′ | 304 | 0.8 | 308 | 1.0 | ||
| τ ring py | A′ | 253 | 0.5 | 243 | 0.3 | Not investigated | |
| τ ring ph | A′ | 154 | 4.6 | 154 | 4.5 | ||
| τ ring ph | A′ | 93 | 1.4 | 93 | 1.2 | ||
- *See Table S1 for definition of symmetry coordinates and Tables S2 and S3 for PEDs calculated using the DFT and MP2 force constants and geometries, respectively. †Approximate description is known to be an oversimplification of the vibration description, where their description in terms of a single, most significant symmetry coordinate was attempted. The detailed description is given in the PED form (Tables S2 and S3). ν, bond stretching; δ, bending; γ, rocking; τ, torsion; ph, phenyl ring; py, pyrone ring. Wherever two approximate descriptions are given, separated by a slash (/) symbol, the left-most corresponds to the approximate description extracted from the PEDs calculated at the DFT(B3LYP)/6-311++G(d, p) level and the second one to that obtained based on the MP2/6-31G(d,p) calculations. ‡Theoretical positions of absorption bands were scaled by a factor of 0.964 in the 4000–2500 cm−1 region, 0.982 in the 2500–1000 cm−1 region and 0.989 in the region below 1000 cm−1. §Theoretical positions of absorption bands were scaled by a factor of 0.938 in the 4000–2500 cm−1 region, 0.956 in the 2500–1000 cm−1 region and 1.014 in the region below 1000 cm−1. || Observed intensities (Intexp) correspond to band integral absorbances (A) normalized by the theoretical intensities (Intcalc) at MP2/6-31G(d, p) level, according to the formula Intexp(i) = A(i).ΣIntcalc/ΣA, where the sums extend to all theoretical bands which have an experimentally observed counterpart. ¶In the low frequency region the torsional vibrations of the pyrone ring were predicted in a substantially different way by the DFT(B3LYP)/6-311++G(d, p) and MP2/6-31G(d, p) methods.
Two points deserve additional comments. First, the IR spectrum of matrix-isolated coumarin exhibits extensive band splitting. This is particularly evident in the case of the intense carbonyl stretching vibration (see Fig. 2), where the corresponding multiplet band spans more than 30 cm−1. As addressed below, all components of this multiplet decrease proportionally during irradiation of the matrix and thus should originate in vibrations of the monomeric coumarin. Such a large splitting cannot be attributed solely to the matrix site-splitting effect. Most probably, the splitting in the C=O stretching region should be related with pronounced anharmonicity of the C=O stretching vibration in coumarin. A similar situation has been observed experimentally for matrix-isolated uracil, which exhibits bands of an extremely complicated shape in the region of the C=O stretching vibration (51). In the latter case, the spacing in multiplet C=O absorptions also exceeded 30 cm−1 and was attributed to Fermi resonances. An analogous spectral behavior, with a strong split of the bands due to the C=O stretching vibrations, was also observed for matrix-isolated pyruvic acid (38).
Secondly, though the general agreement of both DFT and MP2 calculated spectra with the experimental data is very good, the two methods perform differently in the different spectral regions. Hence, the DFT method fits better the experimental data in the 1600–1300 cm−1 spectral range, while the MP2 method performs better in the low frequency spectral region (below 1000 cm−1). In the 1300–1000 cm-1 region, both methods have their advantages: the DFT method better predicts the relative intensities, while the MP2 method provides the better relative frequencies, compared to the experimental spectrum. This is a consequence of the different way the two methods take into account electronic correlation effects. Indeed, it has been shown (52) that in calculations of cyclic molecules (especially those with strained bonds and angles) accounting for nondynamical electronic correlation may be particularly relevant, resulting in a better performance of the MP2 method compared with the DFT approach, specially for highly anharmonic low frequency vibrations. This point will be developed in the next section.
Photochemical experiments
Once the spectrum of matrix-isolated coumarin was interpreted, the sample was subjected to in situ UV irradiation. By analogy with α-pyrone (53) it was expected that the photochemistry of matrix-isolated coumarin might depend on the wavelength of the UV-irradiation. With this idea in mind, the matrix was subjected to a series of irradiations where the incident light was filtered by different long-pass filters, similar to those used in the study of α-pyrone. However, somewhat surprisingly, no changes in the absorption spectra were observed when consecutive irradiations were carried out with filters transmitting light with λ > 337, 315, 285 and finally λ > 235 nm. The photoreaction started to occur, slowly, only when the sample was irradiated with λ > 200 nm through the outer quartz window of the cryostat. Photolysis of the compound manifested itself by the decrease in the intensity of bands initially present in the spectrum. It is particularly interesting to comment on the behavior of the absorptions in the carbonyl stretching region of coumarin during irradiation (Fig. 3). All components of the multiplet band decreased uniformly and proportionally during irradiation. This is an indication that the nature of the splitting observed in the C=O stretching region cannot be related with the association. On the contrary, all bands originate in the matrix-isolated monomeric species, and the observed splitting should be related to the anharmonic nature of the carbonyl stretching vibration in coumarin. For example, the anharmonicity and a strong coupling between the C=O, C=C and C≡N stretching vibrations were recently reported in a similar system, 2-cyanocoumarin (54).
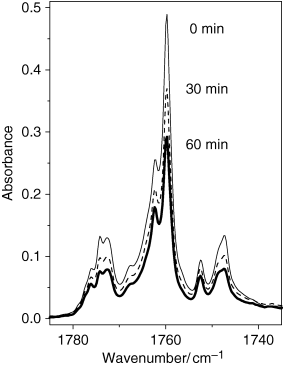
Carbonyl stretching region of the experimental infrared spectra of coumarin isolated in an argon matrix at 10 K. The upper trace (thin line): A freshly deposited, nonirradiated matrix (0 min). The middle trace (dashed line): After 30 min of irradiation with the unfiltered UV-light from Hg(Xe) lamp (λ > 200 nm). The lower trace (bold line): After 60 min of irradiation (λ > 200 nm). Note that the spectrum decreases proportionally over the entire region indicating the monomeric nature of the absorption multiplet.
Concomitant with the consumption of coumarin, new bands appeared in the spectra of the irradiated matrix. Although the photochemical response of matrix-isolated coumarin was found to occur at different wavelengths compared with the matrix-isolated α-pyrone, it can be expected that photochemical transformations of the two compounds present some similarities. The photochemistry of α-pyrone has been extensively investigated in the past for the compound in solution and was also recently studied for the matrix-isolated monomer (53,55–61). Upon UV (λ > 337 nm) excitation, α-pyrone has been shown to undergo a Norrish Type I ring-opening reaction leading to the production of the open-ring conjugated aldehyde-ketene in the Z configuration of the aldehyde and ketene groups with respect to the central C=C bond. The UV irradiation with higher energies (λ > 285 nm) promoted conversion of the Z form of the aldehyde-ketene into the energetically most stable E form (53). Concomitantly, irradiation with λ > 285 nm led also to the photoproduction of the Dewar valence isomer of α-pyrone (2-oxa-3-oxobicyclo[2.2.0]-hex-5-ene). Upon subsequent λ > 235 nm irradiation, the Dewar isomer underwent further photolysis to give rise to a cyclobutadiene complex with carbon dioxide (53). The important experimental finding is that different photochemical channels in α-pyrone are triggered by UV-irradiation of different wavelengths. Several substituted α-pyrones isolated in cryogenic inert matrices were shown to follow essentially the two main reaction paths observed for nonsubstituted α-pyrone (ring-opening and ring-contraction followed by decarboxylation) and the preferred reaction channel was found to depend considerably on the substituents (62–64).
It has been proposed (65,66) that the α-cleavage process leading to ketene-type photoproducts originates from excited states with nπ* character, whereas formation of Dewar isomers should proceed starting from excited ππ* states. In α-pyrones the S1 state is of nπ* character (67), and the nπ*-type photochemistry should be favored for such compounds, especially when they are free of any substituents. The experimental photochemical results obtained for matrix-isolated α-pyrone and substituted α-pyrones (53,62–64) fully confirm these expectations, in particular the considerably stronger preference for the α-cleavage process over the Dewar formation in the case of nonsubstituted α-pyrone.
Besides the two photochannels similar to α-pyrone (ring-opening and ring-contraction followed by decarboxylation), coumarin may exhibit an additional photochemical reaction pathway. According to the results of photochemical studies of coumarin in the gaseous phase (36), the molecule may also undergo decarbonylation, with formation of benzofuran and carbon monoxide.
Selected fragments of the experimental spectra resulting from irradiation of matrix-isolated coumarin are presented in Fig. 4. The experimental spectra of the irradiated matrix provide evidence for all three different photoreaction channels described above and presented in Scheme 2: (a) ring-contraction followed by decarboxylation (CO2 absorption), (b) ring-opening (ketene absorption, designated in Fig. 4 as Z and E), (c) decarbonylation (CO absorption).
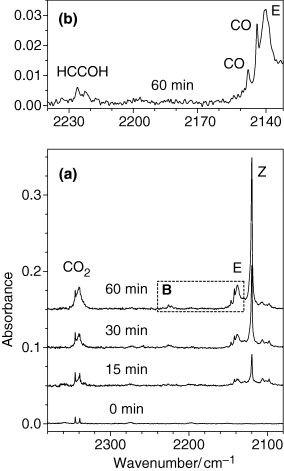
Fragments of experimental infrared spectra (2370–2080 cm−1 range) of coumarin isolated in an argon matrix at 10 K. Frame a. The lowest trace: A freshly deposited, nonirradiated matrix (0 min). The weak doublet at 2345/2339 cm−1 is due to residual impurity of matrix-isolated CO2 monomers. Three upper traces: Spectra of the UV-irradiated (λ > 200 nm) matrix at different stages of irradiation (15, 30 and 60 min total). Frame b [corresponds to the dashed rectangle “B” in frame (a)]. Assignments of bands due to photoproducts are indicated in the figure. Z and E stand for open-ring ketene isomers I and II, respectively. Spectra in frame a are shifted along ordinate for clarity.
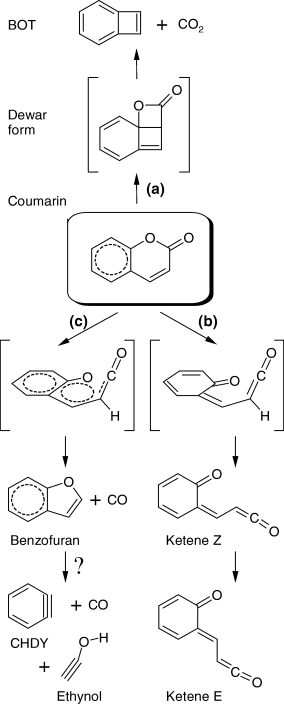
Proposed photolytic reaction pathways resulting from UV (λ > 200 nm) irradiation of matrix-isolated coumarin. Structures in brackets are either not detected [Dewar form, channel (a)] or transition states [channels (b) and (c)]. The reaction marked by question mark is tentative. BOT = bicyclo[4.2.0]octa-1,3,5,7-tetraene (benzocyclobutadiene); CHDY = cyclohexa-1,3-dien-5-yne (benzyne).
In order to shed light on the structures and energies of the species appearing in the matrix upon UV-irradiation, a special attention in this work was paid to the theoretical simulation of possible products resulting from unimolecular photochemical reactions. The DFT calculations failed in predicting stable structures for complexes formed between molecules that can be produced in the same matrix cage upon photolysis, while the MP2 calculations were successful. The energies of possible photoproducts calculated at the MP2/6-31G(d,p) level are summarized in Table 3, while relevant structures are shown in Fig. S1.
| Structure* | Relative energy† | C=O stretching‡ | Relative energy¶ | ||
|---|---|---|---|---|---|
| Electronic | E+ZPVE | Frequency§ | Intensity|| | ||
| Coumarin | 0.0 | 0.0 | 1837.5 | 422.3 | 0.0 |
| Dimer A | 62.5 | 50.8 | 2113.3 | 17.3 | 47.6 |
| Dimer B | 62.7 | 50.9 | 2113.0 | 18.0 | 47.3 |
| Dimer C | 64.0 | 52.5 | 2123.7 | 23.7 | 54.4 |
| Dimer D | 64.3 | 52.6 | 2118.5 | 23.5 | 54.4 |
| Dimer E | 64.2 | 52.7 | 2123.9 | 22.1 | |
| Dimer F | 65.1 | 53.2 | 2118.1 | 23.3 | |
| Dimer G | 66.6 | 54.8 | 2119.6 | 21.7 | |
| Dimer H | 67.1 | 55.0 | 2123.8 | 32.3 | |
| Dimer J | 67.0 | 55.1 | 2117.2 | 22.7 | |
| Dimer K | 67.9 | 55.8 | 2116.6 | 22.2 | |
| Dimer P | 176.0 | 161.4 | 2442.8 | 291.8 | 154.7 |
| Dimer Q | 176.9 | 162.0 | 2444.8 | 312.4 | 155.0 |
| Dimer R | 182.4 | 167.6 | 2441.9 | 360.8 | 166.5 |
| Ketene I | 187.6 | 179.3 | 2206.2 | 1670.2 | |
| Ketene II | 198.9 | 190.3 | 2212.3 | 1389.5 | |
| Ketene III | 207.5 | 198.6 | 2199.6 | 933.4 | |
| Dewar | 298.9 | 297.4 | 1902.9 | 435.6 | |
| TS1 | 255.6 | 244.4 | |||
| TS2 | 358.6 | 348.4 | |||
| TS3 | 373.7 | 361.3 | |||
- *All listed structures are depicted graphically in Fig. S1. Dimers A-K are complexes [benzofuran + CO]; Dimers P-R are complexes [bicyclo[4.2.0]octa-1,3,5,7-tetraene (BOT) + CO2]; TS1 is a transition state for isomerization between coumarin and Ketene I; TS2 and TS3 are transition states for decarbonylation. †MP2/6-31G(d,p) level. All energies are in kJ mol−1 relative to coumarin; the absolute calculated values for coumarin are equal to −495.569534 Eh (electronic only) and to −495.442307 Eh (electronic + zero-point vibrational energy). ‡All listed species have only one vibration in the 1800–2500 cm−1 region, which can be described as (1) C=O stretching for coumarin, its Dewar isomer, and dimers A–K; (2) antisymmetric O=C=O stretching for Dimers P and Q and (3) antisymmetric C=C=O stretching for ketenes I–III. §Frequency nonscaled, in cm−1. || Intensities in km mol−1. ¶MP2/6-311++G(d,p) level. All energies are in kJ mol−1 relative to coumarin; the absolute calculated value for coumarin is equal to −495.766206 Eh (electronic only).
As seen from Table 3, among the possible photoproducts of coumarin the most energetically favoured species are dimers A-K, resulting from decarbonylation of the compound [channel (c)]. In the calculations, many stable dimer structures were found, but probably the number of possible dimers is even higher. In the conformational search we explored only those structures where the detached CO molecule remains in the vicinity of the oxygen atom of benzofuran, i.e. the geometries which imply a minimal displacement of the CO molecule from its original position in the starting compound. It is likely that the potential energy hypersurface of the dimer [benzofuran + CO] has additional local minima. At the chosen level of theory [MP2/6-31G(d,p)] the electronic energies of the optimized structures range from ca 62 to 68 kJ mol-1 compared with coumarin, and after accounting for the zero-point vibrational energies the dimers become more stabilized, their energy relative to coumarin being only ca 50–56 kJ mol-1. The calculated vibrational spectra of all dimers do not exhibit any imaginary frequencies, i.e. these structures are true minima on the potential energy surface of the system. Among all calculated dimers, the most stable structures result from stacking geometries, where the CO molecule floats over the furan sub-unit of benzofuran at the distance of ca 3.1 Å. Optimization of selected structures was repeated at the MP2 level with diffuse functions added on all atoms [MP2/6-311++G(d,p)] and using split valence triple-ζ basis set instead of double-ζ basis set. This allowed for a better theoretical description of long-range interactions in the studied systems. The MP2 calculations with the split valence triple-ζ basis set augmented with diffuse functions resulted in further stabilization of dimers with respect to coumarin. The relative energies (electronic only) of dimers A and B with the stacking orientation of the components (CO and benzofuran) decreased from ca 62 to 47 kJ mol-1 with the increase in the basis set (stabilization of ca 15 kJ mol−1). The stabilization of the planar dimers C and D was ca 10 kJ mol−1 (see Table 3). At the available computational resources, calculation of vibrational spectra was not feasible at the MP2/6-311++G(d,p) level. However, the optimized geometries at both levels remained similar: separation between CO and benzofuran amounted again to ca 3.1 Å. This suggests that the structures of dimers do correspond to the true minima. Assuming that the zero-point vibrational energies at the two theory levels are equal, one may predict that the energies of the most stable [benzofuran + CO] dimers (stacking dimers A and B) are ca 35 kJ mol−1 relative to coumarin. An additional factor may contribute to the stabilization of the photoproduced dimers in matrices. Unlike the gaseous phase, for the matrix-isolated compound the decomposition products usually are confined to the same matrix cavity. Such a spatial limitation may serve as an additional stabilization factor for the dimers photoproduced from coumarin.
The other relevant possible photoproducts of coumarin have direct analogy with those photochemically produced from α-pyrone, with an additional phenyl ring attached to the remainder of the photochemically transformed pyrone sub-unit. Decarboxylation [channel (a)] leads to a dimer of carbon dioxide with bicyclo[4.2.0]octa-1,3,5,7-tetraene (BOT, benzocyclobutadiene). As a possible intermediate in the formation of this dimer, the Dewar analog of coumarin was considered (see Scheme 2). For isomerization [channel (b)] three stable structures of the open-ring ketene were found (Scheme 3). Finally, geometries of transition states for ketene formation as well as for decarboxylation were calculated. All these structures are depicted graphically in Fig. S1 and have very high relative energies: starting from ca 160 and up to ca 300 kJ mol−1 compared with coumarin (see Table 3).
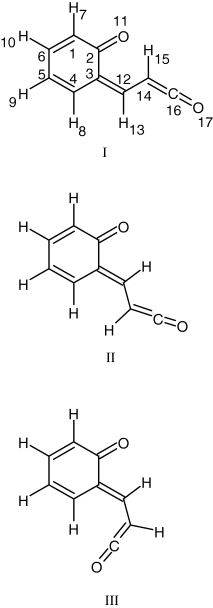
Conformers of the open-ring ketene derived from coumarin, with adopted atom numbering scheme. Conformer I belongs to the Z type, while II and III belong to the E type.
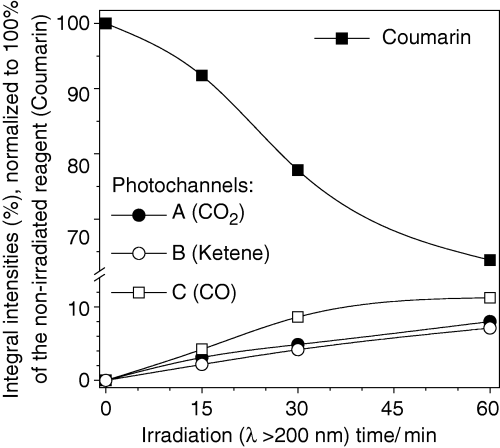
Time evolution of populations of selected photoproducts generated upon UV irradiation (λ > 200 nm) of coumarin isolated in an Ar matrix at 10 K. Experimental integral intensities are reduced by calculated intensities and normalized. Three photochannels were considered: (a) decarboxylation (formation of CO2 and BOT); (b) isomerization (formation of the open-ring ketene); (c) decarbonylation (formation of CO and benzofuran). Estimation is based on the bands due to C=O or C=C=O stretching vibrations. Results for photochannels (b) and (c) include cumulative intensity over two absorption peaks (see Fig. 4), and normalization was carried out using average calculated intensities for two most stable calculated photoproducts (ketenes E and Z, and dimers A and B). Note ordinate break.
The choice of species used in the estimation of abundances deserves additional comments. For the dimeric photoproducts (A-K and P-R) it was assumed that the most energetically stable geometry is formed in the matrices. This assumption was based on the fact that the optimization procedure revealed that CO- and CO2-containing dimers have very low forces for displacements of CO and CO2 molecules around their counterparts, benzofuran and BOT, respectively. The corresponding low barriers can be easily overcome in matrices and, in the conditions of low-temperature environment, dimers should adopt their energetically most stable geometries.
The most stable CO2-containing photoproducts are stacking complexes between CO2 and BOT (dimers P and Q, Fig. S1). The rotation of the CO2 part with respect to BOT does not produce any significant change in the energy of the complex and multiple orientations are possible. Probably because of this reason, the absorption band due to matrix-isolated photoproduced CO2 is broadened (see Fig. 4a).
Regarding the [benzofuran + CO] dimer, the calculations predicted that the two lowest energy stacking structures (dimers A and B) are practically isoenergetic. These species differ only by orientation of the CO molecule with respect to benzofuran; they are good candidates for the experimentally observed bands at 2146 and 2142 cm−1 (Fig. 4b). The observation of the CO absorptions at these frequencies is an indication that the CO molecules stay in the same matrix cage with benzofuran and form a complex, as these are usual frequencies for CO complexes (68,69). It must be noted that the band centered at 2138 cm−1 cannot be attributed completely to the absorption of CO. The absorption of carbon monoxide is very weak in IR (average calculated intensity over all dimers is ca 22 km mol−1, see Table 3) and if the whole area below the absorption band at 2138 cm−1 would originate in CO, this would require the amount of photoproduced CO molecules to be three times more than the amount of consumed coumarin. On the other hand, the whole absorption in the 2150–2100 cm−1 region cannot be entirely attributed to ketene species either. Indeed, in contrast to CO, the ketene gives rise to an extremely strong IR absorption (above 1000 km mol−1). Then, attributing the full 2150–2100 cm−1 region to the absorption of the ketene would imply that the total amount of photoproduced species is too little compared with the amount of consumed coumarin. The obvious compromise is that both CO and ketene species contribute to the absorptions in the 2150–2100 cm−1 region. However, it is less obvious how to separate these two contributions. A fairly reasonable result is obtained when the CO absorption was attributed to the weak bands centered at 2146 and 2142 cm−1 (as shown in Fig. 4b), and the remaining strong absorptions at 2138 and 2120 cm−1 were assigned to open-ring ketenes (Z and E in Fig. 4a). Under these conditions, the normalized amount of the consumed reagent corresponds to the normalized amount of photoproduced species.
The ketene produced from coumarin may exist in three stable conformations (see Scheme 3). The most stable form (form I in Scheme 3) has the Z orientation with respect to the central C3=C12 bond, while forms II and III are E isomers. The Z isomer exhibits a C–H···O= intramolecular hydrogen bond forming a six-membered ring and, in the ground electronic state, it is predicted by the DFT calculations to be more stable than the other two conformers (forms II and III in Scheme 3) by 12.9 and 23.4 kJ mol−1, respectively. At the MP2 level these differences in energy amount to 11.0 and 19.3 kJ mol−1, respectively (see Table 3).
The presence in the spectra of absorptions due to two ketene conformers implies that both the Z and at least one of the E isomers with respect to the orientation of carbonyl and ketene groups are formed in the irradiated matrix. This observation is in agreement with recent studies of matrix-isolated α-pyrone (53) and its sulfur analogs (64) where the formation of the Z and E photoproducts was experimentally observed. Assignment of the bands due to the Z and E isomers in the 2150–2100 cm−1 spectral region was based on the relative positions of the two absorptions: ketene I (Z), absorbs at lower frequencies, compared to ketene II (E, see Fig. 4 and Table S4).
The time evolution of the bands ascribed to the photoproducts resulting from the different observed reaction paths revealed that all products appear concomitantly, with approximately equal probabilities and grow in parallel at all stages of irradiation. Although Fig. 5 seems to show that the CO-containing species [photochannel (c)] are formed in a slightly higher amount than those produced in photochannels (a) and (b), the experimental error is also higher in case (c), due to two facts: (1) very low intrinsic intensity of the CO absorption and (2) overlapping of the CO absorption with that of ketene E [see frame (b) of Fig. 4], which reduces the certainty in the choice of baseline and may introduce an additional error in the results of integration.
In summary, the proposed mechanism of photolysis of matrix-isolated coumarin consists essentially of three main reaction pathways (see Scheme 2). Two of them [(a) and (b)] are similar to those previously observed for α-pyrone (53) and α-pyrone derivatives (62–64). The compound can undergo isomerization to the Dewar form (2-oxatricyclo[4.4.0.01,4]deca-5,7,9-trien-3-one), with subsequent decarboxylation and formation of bicyclo[4.2.0]octa-1,3,5,7-tetraene (BOT, benzocyclobutadiene) and carbon dioxide [channel (a)] or a ring opening reaction leading to production of the isomeric conjugated ketene [channel (b)]. The third pathway [channel (c)] consists of decarbonylation, leading to the formation of benzofuran and carbon monoxide. As mentioned before, the photochemistry of type (c) has been previously reported for coumarin in the gaseous phase (36). Yatsuhashi and Nakashima (36) mentioned that the photochemically produced benzofuran underwent further decomposition upon UV irradiation. However, the authors did not specify what the final products of such decomposition were. We now suggest, tentatively, that benzofuran may undergo cleavage of the five-membered ring and give rise to benzyne (CHDY—cyclohexa-1,3-dien-5-yne) and ethynol (H−C≡C−O−H). A band ascribable to the C≡C stretching vibration of ethynol was observed as a weak doublet between 2230 and 2220 cm−1 in our experiment (see Fig. 4b). The DFT calculations predict that it is the strongest band of ethynol in IR (163 km mol−1) and the position of this band is predicted at 2237 cm−1. However, this band in our experiments is extremely weak indicating that the secondary photoreaction is as difficult as the photodecomposition of coumarin itself. The second strongest absorption of ethynol in IR (119 km mol−1) is predicted to be at 3716 cm−1 and is ascribed to the OH stretching vibration. In the experiment, a very weak band of a photoproduct was found to appear at ca 3327 cm−1. This is a plausible frequency for an OH group involved in intermolecular H-bonding interactions.
The presence of several different photoproducts in the photolysed matrix is also evident from other spectral regions (see Table 4, with proposed assignments of bands due to the identified photoproducts). The strongest bands in the fingerprint region of the calculated spectra of all photoproducts are predicted to appear around 750 cm−1. This is easy to explain: all photoproducts include an aromatic six-membered ring with four C−H groups attached to it. Such molecular fragment has a very characteristic vibration, strong in IR, corresponding to the all in-phase out-of-plane CH bending (γC−H) mode. A very strong IR absorption appearing at this frequency was experimentally found (see Table 4) for gaseous benzofuran (70) and for matrix-isolated monomeric benzocyclobutadiene (71,72). The molecule of coumarin also has the γC−H vibration at similar spectral position; this vibration serves as a good reference point for comparison with the spectra of the photoproducts. Seeing the situation from the other perspective, we may say that the presence of the absorption band around 750 cm−1 in the spectra of photoproducts implies that the aromatic six-membered ring with four C−H groups is not affected by irradiation and all photochemical changes of coumarin should be related to the reorganization of the pyrone sub-unit. This reasoning reduces the number of possible photochemistries to channels (a), (b) and (c) only. We could not find any other mechanisms/reaction schemes which preserve the six-membered benzene ring intact.
| Photoproduct | Calculated frequency† | Calculated intensity | Observed frequency‡ | |
|---|---|---|---|---|
| This work | Literature data | |||
| Ketene | ||||
| II | 2115 | 1389.5 | 2138 | |
| I | 2109 | 1670.2 | 2122, 2120, 2114, 2108 | |
| I | 1609 | 155.4 | 1604 | |
| II | 1555 | 187.4 | 1563 | |
| I | 1549 | 31.6 | 1557 | |
| II | 1530 | 666.6 | ∼1514 | |
| I | 1513 | 647.3 | 1505 | |
| II | 1455 | 15.9 | 1460 | |
| I | 1447 | 19.5 | 1456 | |
| I | 1362 | 8.6 | 1360(?) | |
| II | 1235 | 50.0 | 1262 | |
| I | 1233 | 90.6 | 1253 | |
| II | 1173 | 63.2 | 1181 | |
| I | 1129 | 37.9 | 1123 | |
| I/II | 1044/1040 | 6.3/19.9 | 1032 | |
| I | 917 | 27.7 | 889(?) | |
| I | 744 | 65.8 | 770–745¶ | |
| II | 732 | 58.3 | 728 | |
| I | 643 | 41.1 | 650–620# | |
| II | 635 | 30.8 | ||
| II | 624 | 41.4 | ||
| [Benzofuran + CO]§ | ||||
| 2020 | 17.3 | 2146/2142 | ||
| 1453 | 14.7 | 1460 | 1457 | |
| 1432 | 24.2 | 1420 | ||
| 1261 | 31.8 | 1278 | 1253 | |
| 1172 | 28.7 | 1181 | 1179 | |
| 1130 | 12.9 | 1123 | 1131 | |
| 1090 | 9.1 | 1098 | 1107 | |
| 1034 | 10.0 | 1032 | 1036 | |
| 889 | 12.3 | 861 | 861 | |
| 754 | 70.2 | 770–745¶ | 767 | |
| 746 | 43.8 | 746 | ||
| [BOT + CO2] || | ||||
| 2335 | 291.8 | 2341 | ||
| 743 | 71.4 | 770–745¶ | 737 | |
| 683 | 34.9 | 690 | 700 | |
| 643 | 16.0 | 650–620# | ||
| 631 | 41.7 | |||
- *See Table S4 for complete calculated spectra of the photoproducts. †Theoretical MP2/6-31G(d,p) positions of absorption bands were scaled by a factor of 0.956 in the 2500−1000 cm−1 region and of 1.014 in the region below 1000 cm−1. DFT calculated frequencies for ketene isomers in the 1600–1300 cm−1 region were scaled by the factor 0.982. ‡Bands in italic were assigned to more than one photoproduct. Between 1650 and 1600 cm−1 absorptions due to traces of water (bending mode) present as impurity in the matrix preclude any detailed analysis. Literature data for benzofuran is for the gas phase (70), for BOT is for the isolated monomer in solid argon (71,72). §All bands are possible to be assigned to both dimers A and B with the exception of the band at 861 cm−1. Because of that, only calculated frequencies and intensities for dimer A are presented in the table, except for that band, where the values presented correspond to those obtained for dimer B. || All bands are possible to be assigned to both dimers P and Q. Thus, only calculated frequencies and intensities for dimer P are presented in the table. ¶In the 770–745 cm−1 region there are multiple bands whose assignment to individual species cannot be made with certainty. However, it is certain that all these species bear the common structural unit: A six-membered benzene ring. #The number of possible contributors for this spectral region is expected to be large, with frequencies differing slightly from each other due to effects of the lifting of degeneracy from the OCO bending vibration due to dimerization (for the BOT/CO2 complex) and inhomogeneous band broadening (for both BOT/CO2 complex and ketenes), so that the resulting broad profile is difficult to be distinguished from the background (see text and also Fig. 6).
Because of the presence of the common structural moiety (six-membered benzene ring), the spectra of the photoproducts are very likely to overlap between them and with the absorptions of coumarin. To unveil the spectra of matrix-isolated photoproducts, the absorption of the parent compound were subtracted from the spectra of irradiated matrices. In order to do that, the spectrum of the nonirradiated matrix, i.e. the spectrum of coumarin, was downscaled and subtracted from the spectrum of the irradiated sample. At different stages of irradiation, different scaling factors were used, chosen to nullify absorptions of coumarin in the spectral regions free of absorptions of the photoproducts. Two selected examples, after 60 and 210 min of irradiation, are presented in Fig. 6 (solid lines, upper frame) along with the spectrum of coumarin (dashed line).

Experimental infrared spectra of coumarin and photoproducts in the region of the C−H out-of-plane and CO2 bending vibrations. Upper frame. Dashed line: Spectrum of coumarin in a freshly deposited argon matrix, prior to irradiation (0 min). Full lines: Difference spectra of photoproducts formed after 60 min (thin line) and after 210 min (bold line) of irradiation with the unfiltered UV-light from Hg(Xe) lamp (λ > 200 nm). The difference spectra were obtained by subtraction of the scaled spectrum of nonirradiated matrix from the spectra of irradiated samples. Lower frame. Theoretical spectra of coumarin (dashed sticks) and selected photoproducts (solid sticks) calculated at the MP2/6-31G(d,p) level of theory. A and B stand for the two most stable dimers (benzofuran + CO); P and Q stand for the two most stable dimers (BOT + CO2). DFT calculations failed to converge for these dimers. Z and E stand for the open-ring ketene species. All calculated frequencies in this region were scaled by a factor of 1.014. Calculated intensities of coumarin are multiplied by a factor of 10. Middle frame. The solid line represents a superposition of spectra A, B, P, Q, Z and E (in the proportions 1.5/1.5/1.0/1.0/1.6/0.4, respectively). It was simulated using Lorentzian functions centered at the calculated frequencies and with bandwidth-at-half-height equal to 4 cm−1.
The experimental difference spectra of photoproducts are compared in Fig. 6 with the simulated spectrum of photoproducts (middle frame). For such a branched photochemistry, in simulation of the vibrational spectra, it is important to know the relative efficiencies of different photochannels. These efficiencies were assessed based on kinetic data (Fig. 5). It was assumed that, after 1 h of irradiation, photoproducts in channels (a), (b) and (c) were formed in the ratio 1:1:1.5 (or 2:2:3). Moreover, the ketene species Z and E [channel (b)], were subdivided in ratio 4:1 (or 1.6:0.4), based on the relative intensities of the respective absorptions in the C=C=O stretching region (Fig. 4). The two most stable dimers in each of the channels [(a), dimers P and Q] and [(c), dimers A and B] were subdivided in the simulation in the equal ratios (1:1 and 1.5:1.5, respectively). Thus, structures A, B, P, Q, Z and E contribute to the simulated spectrum in the proportions 1.5/1.5/1.0/1.0/1.6/0.4, respectively (Fig. 6, middle frame).
The difference spectra in Fig. 6 confirm that the bands due to photoproducts overlap slightly with the absorption due to coumarin, but still are distinct. All further discussion is based on the results of MP2 calculations, as they correspond much better to the experimental observations. DFT calculations fail to predict correctly not only frequencies, but also the forms of vibrations in this spectral region. For example, both benzofuran and benzocyclobutadiene have four H atoms which are connected to the benzene sub-unit and two other H atoms that are connected to the second ring, either four- or five-membered. In the DFT calculations, the out-of-plane vibrations of all six hydrogen atoms in these molecules are strongly mixed and contribute to the same vibrational mode (usually all in-phase vibrations), giving rise to a band close to that of coumarin (observed around 750 cm−1). On the other hand, in the MP2 calculations, the out-of-plane CH vibrations of hydrogens attached to different rings do not mix.
In benzofuran (complexed with CO), the difference in the frequencies of these two modes amounts to ca 8–9 cm−1 resulting in a very characteristic doublet structure of the absorption band due to the out-of-plane CH vibrations of the photoproduct. The whole doublet is slightly shifted to lower frequencies compared to the vibration of coumarin, both in the experiment and in the MP2 calculations (see Fig. 6).
The calculated spectrum of the dimer [BOT + CO2] represents a more interesting case and deserves a special description. First, the frequencies characteristic of concerted out-of-plane vibrations of four CH groups connected to the benzene ring remain at 743–745 cm−1 (Tables 4 and S4), close to those of benzofuran, thus contributing to the doublet-like cumulative band of the photoproducts (see solid line in the simulated spectrum shown in Fig. 6). Secondly, the frequencies of the out-of-plane vibration of the two CH groups connected to the four-membered ring are now predicted much lower, at ca 683 cm−1, bearing also a considerable IR intensity. The separation of the two vibrations (associated with the CH-quartet of the phenyl sub-unit and the CH-pair of the cyclobutadiene sub-unit) amounts now to 60 cm−1. This is in agreement with the experimentally observed separation of 56 cm−1, and explains the appearance in the spectra of photoproducts of the band at 690 cm−1, which DFT calculations were not able to predict. Indeed, there is a good agreement of the relative position of this band compared to the peak of coumarin at ca 680 cm−1, both in the experiment and in the MP2 calculations. The last result is particularly important, both experimentally and theoretically, as it unequivocally confirms the occurrence of the photochannel (a), related to the decarboxylation of coumarin. No other photoproducts are predicted to absorb at a frequency close to 690 cm−1. Moreover, this frequency is practically not affected by the orientation of the CO2 molecule in the dimer, thus all types of dimers contribute to a single strong absorption.
Further evidence of the decarboxylation channel (a) can be obtained from the absorptions of the CO2 molecules in dimers. The high symmetry of the CO2 monomer (D∞h) is lifted when it makes part of a complex, and lifting of degeneracy from the OCO bending vibration results in formation of a doublet. This is exactly what occurs in the case of the dimer [BOT + CO2]. In the two considered [BOT + CO2] dimers, P and Q, the four OCO bending vibrations (two doublets) were predicted at four different frequencies: ca 631, 639, 642 and 643 cm−1. Considering the possibility of existence of additional different geometries for dimers of this type, it is easy to expect that the absorption caused by the CO2 bending vibrations will be “smashed” over a large frequency range due to the effect of the inhomogeneous band broadening. This fact is already noticeable in the shape of the absorption of the cumulative spectrum between 620 and 650 cm−1 (see Fig. 6), in consideration of two different [BOT + CO2] dimers only, besides contributions from ketenes.
After prolonged irradiation, one may note an increase in the absorption band around 663 cm−1. No strong bands at this frequency are predicted for any photoproduct. On the other hand, this frequency is characteristic of absorption resulting from monomeric CO2 isolated in argon matrix. Increase in the corresponding absorption may indicate that a part of CO2 molecules, produced together with BOT, escape from the initial matrix cavity and travel across the matrix as monomers.
It is also worth mentioning that the mechanism proposed for the production of CO2 by elimination of this species from the Dewar analog of coumarin is similar to that previously observed for α-pyrone and other α-pyrone derivatives, for which the corresponding Dewar isomers could be experimentally characterized and the progress of the reaction followed spectroscopically (53,62).
The presence of photoproducts in the matrix can also be verified in other spectral regions. Figure S2 shows two fragments of spectra. In the 1620–1340 cm−1 range, the ketene photoproducts are expected to absorb in spectral regions free from band of other photoproducts and of coumarin itself. The strong experimental bands appearing at 1604, 1514 and 1505 cm−1, as well as a few weaker absorptions, can be unequivocally attributed to the vibrations of ketenes, and confirm the occurrence of the photochannel (b) (Fig. S2a). This observation reinforces conclusions drawn from the analysis of results in the C=C=O stretching region (Fig. 4).
Photoproducts in channel (c) were the most difficult to identify. The majority of CO and benzofuran absorptions are predicted to be very weak (note, for example, squares in Fig. S2b). The strongest bands of benzofuran have a very moderate intensity in IR (below 70 km mol−1) and their identification is complicated by the fact that they coincide with bands of coumarin or with those due to other photoproducts (Fig. 6 and Fig. S2b). Two bands of the absorptions of benzofuran which stay “apart” are predicted at 1261 and 889 cm−1, and they can be correlated with the bands of photoproduct appearing at 1278 and 861 cm−1, respectively. These bands correlate well with the two very strong absorptions of gaseous benzofuran observed experimentally at nearly the same frequencies (1253 and 861 cm−1) (70).
Mechanism of coumarin photochemistry: similarities and contrasts with related molecules
One can make some interesting comparisons between the photochemistries of matrix-isolated and gaseous coumarin as well as between matrix-isolated coumarin and related molecules. As mentioned above, there are similarities between UV-induced processes in matrix-isolated coumarin and matrix-isolated α-pyrone. On the other hand, the striking difference is that the photochemical cleavage of coumarin can be experimentally achieved only upon UV-excitation with λ > 200 nm, while in α-pyrone the ring-opening reaction starts readily upon irradiation with λ > 337 nm. This discrepancy cannot be explained in terms of different energy gaps between the electronic ground states and the lowest excited states in two compounds. In coumarin the two lowest singlet states were found to have energies of 29 100 cm−1 (n,p*) and 32 800 cm−1 (p,p*) (27), while in α-pyrone the corresponding energies were comparable or slightly higher: 30 200 cm−1 (n,p*) and 35 000 cm−1 (p,p*) (67). From the energy λ > 200 nm, which that could afford cleavage of coumarin molecule (λ > 200 nm), and comparison with the UV absorption spectrum of coumarin at room temperature (31), it can be deduced that the target electronic excitation corresponds to the band at ca 210 nm (in ethanol). It is equal to ca 47600 cm−1, which according to calculations in Ref. (27) is as high as S5. Only such a high excitation is capable of inducing the photochemical processes in the matrix. Four singlet states and five triplet states are situated below this level! We suggest the following arguments to justify this behavior:
- (i)
The presence of the additional phenyl ring attached to the pyrone sub-unit results in an increase in the density of electronic states in coumarin in the vicinity of S1 and S2, compared to α-pyrone. In coumarin, the S1 (n,π*) state is almost isoenergetic with T3 (n,π*): 29100 ± 500 and 28000 ± 300 cm−1, respectively (27). This proximity can result in a very effective intersystem crossing and subsequent quenching, via T2 to T1 (22000 ± 300 cm−1). The lowest triplet state is probably lying too low in energy to induce ring cleavage.
- (ii)
The increase in the number of atoms in coumarin compared to α-pyrone results in the increase in intramolecular vibrational degrees of freedom that can serve as intermediates for the processes of nonradiative dissipation of energy.
- (iii)
Steric hindrances may also reduce efficiency of the ring-opening reaction. We calculated the potential energy profile for the cleavage of the O1−C2 bond in coumarin. The results are presented in Fig. 7. When the reaction coordinate approaches 2 Å, the relative energy of coumarin starts to increase much faster. This can be related, in part, to the fact that the two neighboring hydrogen atoms of coumarin, H13 and H17, enter in a strong repulsive interaction with increase in the O1−C2 distance.
- (iv)
The effects of π-electron delocalization in the two systems are different. In the α-pyrone molecule, the ring-opening reaction results in an increase in the number of double bonds, which can be considered as a stabilizing contribution in terms of the molecular π-system. On the other hand, in coumarin the opening of the pyrone sub-unit ring affects the π-electronic system of the neighboring phenyl ring, partly destroying its aromaticity, which can be considered as a generally destabilizing factor. Indeed the energies of the two similar open-ring species (ketene I) relative to the closed-ring counterparts are equal to 75 kJ mol−1 in α-pyrone (53) and 140 kJ mol−1 in coumarin!
- (v)
Competitive photolysis processes are stronger in coumarin. Indeed, the present experimental data indicate that, along with the ring-opening reaction (isomerization), the decarboxylation and decarbonylation reactions do also occur. In α-pyrone, because the ring-opening reaction occurs at lower excitation energies than decarboxylation, such competing mechanisms are not operative. In coumarin, induction of the three observed photochemical channels requires excitation of the molecule to a state as high as S5 in order to provide a sufficient excess of energy to start the different types of processes. Note that the increase in excitation energy in α-pyrone led to simultaneous occurrence of both ring-opening and decarboxylation reactions (53).
- (vi)
The competitiveness in the different photochannels can be also seen from another point. We carried out a series of potential energy scans for ring-opening and for decarbonylation of coumarin. For the ring-opening process, the results were predictable and similar to those in α-pyrone. As there is no minimum for any open-ring geometry in the vicinity of the ketene conformation depicted in Scheme 4 (see also Fig. 7 for the potential energy profile), the transition state between the closed-ring coumarin and the open-ring ketene I represents a geometry where the O=C=C–H group is situated in the perpendicular plane regarding the rest of the molecule (see TS1 in Fig. S1).
Surprisingly, two transition states which were found for decarbonylation (TS2 and TS3 in Fig. S1) resemble very much TS1 regarding the orientation of the ketene moiety. One of the notable differences between TS1, on one side, as opposite to TS2 and TS3, on the other side, lies in the aromaticity of the phenyl sub-unit of the molecule. However, the proximity on the potential energy surface of the molecular geometries for the mentioned transition states may imply the existence of an efficient “cross-road” in the vicinity of the isomerization and decarbonylation photochannels. It should be noted that our optimizations of the transition states were carried out at the electronic ground states. However, the geometries of transition states that we found for coumarin are very close to the geometry for the ring opening of coumarin sub-unit in psoralen (73), which was found as a conical intersection of S0 and S1 potential energy hypersurfaces. Even more interesting is the fact that Tatchen and Marian (73) reported difficulties in the optimization of that geometry using the time-dependent DFT approach. It is then possible that in psoralen there is a close proximity of different excited states and that geometrically similar transition states lead to different products.
- (vii)
As regards the effects of collisional deactivation by the matrix gas, in the gas-phase study of the photochemistry of coumarin (36), it was found that the initial intermediate, which was formed with the laser pulse, was immediately deactivated in the presence of 570 torr of nitrogen. The addition of nitrogen effectively suppressed both the formation of benzofuran and the depletion of coumarin. Applying this observation to the matrix isolation technique, it is clear that the matrix environment is a very abundant and effective quencher for the UV-induced photochemical processes. However, notwithstanding the presence of this quencher, the matrix-isolated coumarin still exhibits propensity to the photochemical cleavage, in contrast to the gaseous coumarin. That is why, the deeper comparative analysis of the gas phase and matrix-isolated photochemistry appears as a very intriguing task not only for coumarin but also in general.
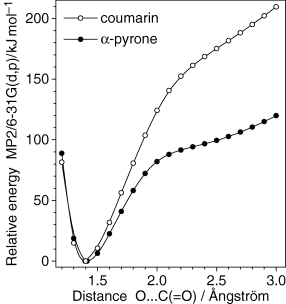
Comparative potential energy profile for cleavage of the C−O α-bond in coumarin and α-pyrone. The C−O bond length was incrementally changed while all other bond lengths and all valence angles were optimized. For simplicity, planarity was imposed on two molecules. The ordinate scale is chosen so that the relative energies of both closed-ring species are equal to zero.
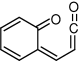
Conformation (not minimum energy structure) of the open-ring ketene where this molecule would adopt the geometry most closely resembling that of coumarin.
Conclusion
The IR spectrum and photochemistry of monomeric unsubstituted coumarin isolated in solid argon at 10 K were investigated. The complete assignment of the IR spectrum of the compound was carried out. In situ UV-induced (λ > 200 nm) irradiation of the compound was found to induce three main photoreactions: (a) ring-contraction to the Dewar coumarin, followed by decarboxylation and formation of bicyclo[4.2.0]octa-1,3,5,7-tetraene (benzocyclobutadiene) and CO2, which in the matrix exist predominantly as a stacked-type complex; (b) ring-opening leading to the formation of the isomeric conjugated ketene, which is produced in both E and Z forms; (c) decarbonylation, leading to the formation of a [benzofuran + CO] complex; further decomposition of benzofuran to produce ethynol + benzyne is suggested. Photochannels (a) and (b) correspond to those previously observed for matrix-isolated α-pyrone and its sulfur analogs (53,62–64), while route (c) is similar to the UV-induced photochemistry of coumarin in the gaseous phase (36). Interpretation of the experimental data is supported by extensive calculations performed at the B3LYP/6-311++G(d,p), MP2/6-31G(d,p) and MP2/6-311++G(d,p) levels.
The obtained results, both experimental and theoretical, were systematically compared with available data for similar compounds, in particular α-pyrone. It was found that the pyrone ring in coumarin exhibits a smaller π-delocalization than in α-pyrone, as a consequence of the presence of the extra phenyl ring, which is reflected in the structural parameters (in particular in the bond lengths) calculated for the two compounds as well as in the HOMA indexes obtained for the pyrone ring in these species. The similarities and contrasts noticed in the photochemistry of coumarin and α-pyrone as well as the substituted α-pyrone derivatives and sulfur analogs were also investigated and possible factors determining them presented.
A systematic analysis of the relative performance of the DFT(B3LYP)/6-311++G(d,p) and MP2/6-31G(d,p) (and in some cases also of the MP2/6-311++G(d,p)) methods in calculations of structures and vibrational spectra of coumarin and its photoproducts also enabled us to conclude that (1) the MP2 method could successfully predict the structures of the complexes formed in a given matrix cage between the molecules formed upon photolysis of matrix-isolated coumarin, while DFT was unable to do so, and (2) the MP2 could better predict the low frequency region (below 1000 cm−1) of the IR spectrum of coumarin and its photoproducts than the DFT method, whereas the opposite trend was noticed for the higher frequency spectral regions.
Acknowledgments
Acknowledgements— This work was funded by Fundação para a Ciência e a Tecnologia (FCT, Grant SFRH/BD/16119/2004 and Projects POCI/QUI/59019/2004 and POCI/QUI/58937/2004, also supported by FEDER), Fundação Calouste Gulbenkian and Eskişehir Osmangazi University Research Foundation (Research Project 200519010).




