Simultaneous numerical representation of soil microsite production and consumption of carbon dioxide, methane, and nitrous oxide using probability distribution functions
Abstract
Production and consumption of nitrous oxide (N2O), methane (CH4), and carbon dioxide (CO2) are affected by complex interactions of temperature, moisture, and substrate supply, which are further complicated by spatial heterogeneity of the soil matrix. This microsite heterogeneity is often invoked to explain non-normal distributions of greenhouse gas (GHG) fluxes, also known as hot spots and hot moments. To advance numerical simulation of these belowground processes, we expanded the Dual Arrhenius and Michaelis–Menten model, to apply it consistently for all three GHGs with respect to the biophysical processes of production, consumption, and diffusion within the soil, including the contrasting effects of oxygen (O2) as substrate or inhibitor for each process. High-frequency chamber-based measurements of all three GHGs at the Howland Forest (ME, USA) were used to parameterize the model using a multiple constraint approach. The area under a soil chamber is partitioned according to a bivariate log-normal probability distribution function (PDF) of carbon and water content across a range of microsites, which leads to a PDF of heterotrophic respiration and O2 consumption among microsites. Linking microsite consumption of O2 with a diffusion model generates a broad range of microsite concentrations of O2, which then determines the PDF of microsites that produce or consume CH4 and N2O, such that a range of microsites occurs with both positive and negative signs for net CH4 and N2O flux. Results demonstrate that it is numerically feasible for microsites of N2O reduction and CH4 oxidation to co-occur under a single chamber, thus explaining occasional measurement of simultaneous uptake of both gases. Simultaneous simulation of all three GHGs in a parsimonious modeling framework is challenging, but it increases confidence that agreement between simulations and measurements is based on skillful numerical representation of processes across a heterogeneous environment.
1 INTRODUCTION
Fluxes of greenhouse gases (GHGs) from soil to the atmosphere are likely to play a significant role as biotic feedbacks to climate change (Ciais et al., 2014; Davidson & Janssens, 2006). Soils under forest, agriculture, and other land-use classes contribute to nearly a quarter of global emissions of GHGs, including carbon dioxide (CO2), methane (CH4), and nitrous oxide (N2O; IPCC, 2014). Production and consumption of these biogenic GHGs are often associated with complex processes, involving carbon (C), nitrogen (N), and oxygen (O2) substrates and inhibitors, and environmental controllers such as temperature, moisture, and transport of solutes and gases (Conrad, 1996), which remain challenging to simulate in ecosystem and earth system models (ESMs).
In this special issue, we present an expansion of a numerical soil process model that is a logical progression of several papers published by our group in the pages of this journal. While the importance of temperature on soil heterotrophic activity has been recognized for over a century (Arrhenius, 1889; Lloyd & Taylor, 1994; Vant't Hoff & Lehfeldt, 1899), and optima at intermediate values of soil moisture have also been well described (Hursh et al., 2017; Linn & Doran, 1984; Moyano, Manzoni, & Chenu, 2013), empirical relationships with these driving factors have had limited value in revealing a mechanistic understanding of soil respiration. Davidson, Belk, and Boone (1998) demonstrated that soil temperature and moisture had opposite seasonal trends in a moist temperate forest, resulting in confounding effects on soil respiration. Drawing on a growing body of research on soil respiration in the 1990s and 2000s, Davidson, Janssens, and Luo (2006) reviewed the emerging recognized need to move beyond mostly temperature functions, such as Q10s, and to mechanistically link temperature and moisture drivers to substrate supply for soil heterotrophic respiration (Rh). Those concepts formed the basis of a parsimonious numerical model that used Dual Arrhenius and Michaelis–Menten (DAMM) kinetics to link soil temperature and moisture to their effects on substrate supply for soil respiration (Davidson, Samanta, Caramori, & Savage, 2012). In the 20 year special issue of this journal, Davidson, Savage, and Finzi (2014) described a vision for how the DAMM model could be conceptually linked to related processes of soil carbon dynamics, which has since been demonstrated in the modular Millennial Model (Abramoff et al., 2018), and how it could be integrated into large ecosystem models, which was since demonstrated by Sihi et al. (2018). Davidson et al. (2014) also proposed that other soil trace gas emissions could be simulated using the DAMM approach.
Here, we offer a new version of DAMM for the greenhouse gases, CO2, CH4, and N2O (hereafter, DAMM-GHG: Dual Arrhenius and Michaelis–Menten-Greenhouse Gas). We use three simultaneous data streams from chamber measurements of CO2, CH4, and N2O fluxes in a New England forest to constrain the DAMM-GHG model, which has a common structure for biophysical processes of production, consumption, and diffusion within the soil, including the contrasting effects of oxygen (O2) as substrate or inhibitor for each process. Another innovation presented here is to represent soil microsite heterogeneity of soil carbon and moisture contents with probability distribution functions (PDFs) and to simulate the production and consumption of each gas at a microsite scale, rather than the traditional modeling approach of using bulk soil means of measured carbon and moisture as model drivers.
Thermodynamic theories suggest that CH4 oxidation (aka methanotrophy) should proceed under aerobic conditions and CH4 production (aka methanogenesis) should be favored under anaerobic (or reducing) conditions (Conrad, 2009; Dean et al., 2018). Production of N2O via nitrification and denitrification processes is known to peak at an optimal intermediate soil moisture content, whereas reducing soil conditions under high water content are thought to be prerequisites for N2O reduction to N2 via classical denitrification (Butterbach-Bahl, Baggs, Dannenmann, Kiese, & Zechmeister-Boltenstern, 2013; Davidson, 1991; Firestone & Davidson, 1989). While a large body of literature generally supports these patterns, there are exceptions that are frequently attributed to spatial heterogeneity within soils and soil microsites.
While the highest rates of net consumption of atmospheric N2O (i.e., N2O reduction) is observed in wetlands, N2O reduction in well-drained upland soils has been observed sporadically for many years (Chapuis-Lardy, Wrage, Metay, Chotte, & Bernoux, 2007; Schlesinger, 2013; Syakila, Kroeze, & Slomp, 2010). Such observations have often been discounted as measurement error or noise. The recent advent of fast response field instruments with good sensitivity and precision has permitted confirmation that upland soils can be small sinks of N2O (Eugster et al., 2007; Savage, Phillips, & Davidson, 2014), and a modest soil sink for atmospheric N2O is now generally accepted as plausible for some sites and times. Increasing soil sink strength of N2O during drought events further increases perplexity, given that drought events generally facilitate soil aeration (Goldberg & Gebauer, 2009). Occasional observations of net emissions of CH4 from well-drained upland soils, although contrary to expectations, are also common (Brewer, Calderón, Vigil, & Fischer, 2018; Cattânio, Davidson, Nepstad, Verchot, & Ackerman, 2002; Keller & Matson, 1994; Silver, Lugo, & Keller, 1999; Teh, Silver, & Conrad, 2005; Verchot, Davidson, Cattânio, & Ackerman, 2000).
Spatial heterogeneity of soil microsites is often invoked to explain net atmospheric uptake of N2O and net emissions of CH4 from well-drained upland soils. Soil heterogeneity at microscales can cause a wide range of microsite redox potentials and concentrations of substrates, which must be accounted for to explain highly skewed distributions of soil GHG fluxes (Parkin, 1987, 1993; Savage et al., 2014; Stoyan, De-Polli, Böhm, Robertson, & Paul, 2000). Because existing ESMs are not able to represent the underlying mechanisms that control variation in enzymatic processes at microsite scales (Tian et al., 2019; Xu et al., 2016), these models often fail to capture the dynamics of soil GHG fluxes, including the so-called hot spots and hot moments (Groffman, 2012; Groffman et al., 2009; Lurndahl, 2016; Saha et al., 2018) or control points (Bernhardt et al., 2017).
Only recently have modeling activities at ecosystem (or landscape) scales begun to shift from the classical framework based on redox strata (or water table position) and mean measured soil moisture to emerging conceptual frameworks that consider heterogeneous environment for production and consumption of GHGs (Ebrahimi & Or, 2018; Keiluweit, Gee, Denney, & Fendorf, 2018; Or, 2019; Wang, Brewer, Shugart, Lerdau, & Allison, 2019; Yang et al., 2017). However, to our knowledge, mechanistic simulation of simultaneous production, consumption, and diffusion of multiple gases (CO2, CH4, N2O, and O2) among multiple soil microsites has not yet been attempted. Numerical representation of microsite production and consumption of multiple GHGs is necessary to simulate concurrent N2O reduction and CH4 oxidation processes in well-drained upland soils (Savage et al., 2014). The overall objective of this work is to demonstrate that the qualitative explanations of microsite heterogeneity can be expressed in a mathematically consistent biophysical process model that is numerically consistent with simultaneously measured fluxes of all three GHGs: CO2, CH4, and N2O.
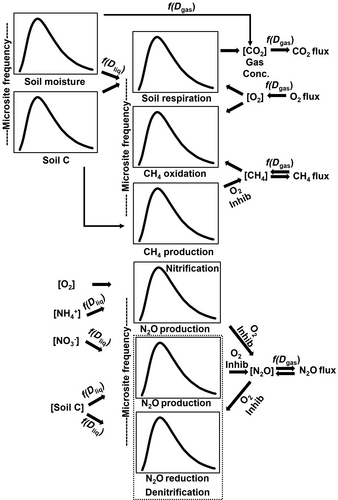
While originally developed for aerobic Rh, here we expand the original core structure of the DAMM model (Davidson et al., 2012, 2014; Figure S1) to represent methanogenesis, methanotrophy, N2O production, and N2O reduction reactions using the same framework and physics for simulating the availability of O2 and other substrates and for diffusion of gases across soil–atmosphere boundary using microsite PDFs (Figure 1; Figure S1). Simultaneously constraining our GHG enzyme kinetic model (i.e., DAMM-GHG) with observations of fluxes of multiple GHGs presents large challenges, because tuning a model to agree with one data stream may cause a poorer fit to a second or third data stream. However, if all data streams can be simultaneously simulated with adequate fidelity and skill, this multiple constraint approach enhances the probability that the parameterization and process representations are realistic and robust. One can never be certain that a model gets the “right answer for the right reason,” but challenging a single model with multiple data streams of related but differing processes, such as CO2, CH4, and N2O fluxes, confers additional credence to its structure and parameterization.
2 MATERIALS AND METHODS
2.1 Site description and data collection
We measured GHG fluxes in a mature boreal-transition forest with a hummock–hollow microtopography, Howland Forest research site (45.20°N, 68.74°W) from central Maine, United States. Mean annual temperature and mean annual precipitation are +5.5°C and 1,000 mm, respectively. Soils of the Howland Forest upland sites are characterized as Skerry fine sandy loam, frigid Aquic Haplorthods. More information on the Howland Forest research site can be found in Fernandez, Rustad, and Lawrence (1993).
High-frequency (sampling frequency: 1 Hz) real-time soil CH4 and N2O fluxes were measured using an Aerodyne quantum cascade laser integrated with soil CO2 flux measurements by LI-COR IRGA assembly. Triplicate chambers were each sampled once every 2 hr. Chamber tops were closed for 5 min and automated fluxes were calculated by fitting a linear regression on the change in headspace GHG concentrations followed by temperature and pressure corrections. We characterized the uncertainty of measurements by the standard deviation estimates for all three GHGs. Soil temperature and soil moisture were measured at each chamber location at 10 cm depth once every hour using a Type-T thermocouple and Campbell Scientific CS616 water content reflectometer probes, respectively, and stored on a Campbell Scientific CR10X data logger (Campbell Scientific). We used daily average values of both drivers (soil temperature and soil moisture) and GHG fluxes for modeling purposes to smooth high measurement noise observed at subdaily timescale. See Savage and Davidson (2003) for more details on our chamber design and automated sampling system. Quality control protocols for soil GHG fluxes can be found in Savage, Davidson, and Richardson (2008) and Savage et al. (2014).
2.2 Modeling scheme
Aerobic and anaerobic processes in soil are linked through heterotrophic dependence on fixed C sources for energy, but with contrasting effects of O2 as either essential substrate or potential inhibitor (Figure 1; Figure S1). To date, most biogeochemical models use separate model versions for simulating soil organic matter decomposition resulting in CO2 emissions and the processes affecting CH4 and N2O emissions, but here we simultaneously simulate biogeochemically linked multiple GHG emissions using the same biophysical framework.
- The measured soil C and soil moisture can be partitioned according to a simulated log-normal PDF, such as a distribution where only a small fraction of microsites has high soil C or high soil moisture.
- Log-normal PDFs of soil C substrates and soil moisture among microsites lead to a simulated PDF of Rh, applying the original DAMM model independently to each microsite within the PDF.
- Simulated microsite CO2 production is aggregated to the chamber scale to estimate Rh contributing to the chamber flux measurement. We then estimate the total soil CO2 flux by adding the contribution of root-derived CO2 fluxes to Rh based on previously measured ratios at the Howland Forest (Carbone et al., 2016; Savage, Davidson, Abramoff, Finzi, & Giasson, 2018; Sihi et al., 2018). A distinct seasonal pattern of the contribution of root-derived CO2 (Ra) to total soil CO2 fluxes (SR) increased from 0.50 in early spring to around 0.65 in early autumn, followed by a declining trend through winter (Figure S2). Total chamber-based measurements of CO2 efflux are used as a constraint for the sum of the simulated root and heterotrophic CO2 production rates across the simulated PDF of microsites.
- The simulated and measured soil CO2 efflux is a reasonable proxy for O2 demand within the soil. The respiration quotient is not exactly unity, but is usually close enough to unity in noncalcareous soils to allow simulation of O2 consumption within the soil based on measurement-constrained simulated CO2 efflux (Angert et al., 2015). Knowledge of respiration quotient would be needed for the application of our DAMM-GHG model to calcareous soils. We assumed that the simulation of O2 consumption by the original version of the DAMM model serves our purpose of estimating the O2 demand (or consumption) here (see Figure S1).
- Microsite PDFs of O2 concentrations are then simulated as a function of O2 consumption rates distributed across microsites and gaseous diffusion rates using the same DAMM functions in Figure S1 driven by air-filled porosity.
- Next, the resulting PDF of O2 concentrations is used to simulate methanogenesis, methanotrophy, N2O production, and N2O consumption at the scale of each of the distributed microsites according to similar Michaelis–Menten and diffusion equations (Figure S1), where O2 serves as either inhibitor or substrate (Davidson et al., 2014). The net CH4 and N2O flux summed across simulated PDFs of microsites are constrained by observed chamber-based fluxes of CH4 and N2O.
We used soluble C as a proxy for the reducing power needed for methanogenesis. However, future studies may explicitly represent specific substrates for acetoclastic and hydrogenotrophic methanogenic pathways, if parameterization of that type of model structure can be constrained by the availability of data on concentrations of organic acids (acetate, formate) and hydrogen (H2), which was not the case for our study. We also assumed that respiration is the dominant pathway of CO2 production in soil. Thus, we did not account for the minor contribution of acetoclastic methanogens to CO2 production and hydrogenotrophic methanogens to CO2 consumption. Likewise, we considered soil respiration is the major sink of O2 and ignored the otherwise small fraction of O2 consumed by methanotrophs.
We added a nitrification module to account for the N2O production during nitrification using the observed seasonal dynamics of ammonium (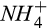 ) in our study area (Fernandez, Lawrence, & Son, 1995). The Howland Forest is a strongly nitrogen-limited system, with porewater nitrate (
) in our study area (Fernandez, Lawrence, & Son, 1995). The Howland Forest is a strongly nitrogen-limited system, with porewater nitrate (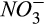 ) concentration always close to detection limits by inductively coupled plasma-mass spectrometry, ICP-MS (Fernandez et al., 1995). N2O production during classical denitrification is mechanistically simulated using seasonally averaged porewater
) concentration always close to detection limits by inductively coupled plasma-mass spectrometry, ICP-MS (Fernandez et al., 1995). N2O production during classical denitrification is mechanistically simulated using seasonally averaged porewater 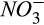 data along with microsite PDFs of soil C and soil moisture. Nitrous oxide is reduced to N2 during classical denitrification following the Hole-in-the-Pipe conceptual model, including possible reduction of atmospheric N2O that diffuses into the soil (Firestone & Davidson, 1989). See Supporting Information (Section S2) for DAMM-GHG model equations.
data along with microsite PDFs of soil C and soil moisture. Nitrous oxide is reduced to N2 during classical denitrification following the Hole-in-the-Pipe conceptual model, including possible reduction of atmospheric N2O that diffuses into the soil (Firestone & Davidson, 1989). See Supporting Information (Section S2) for DAMM-GHG model equations.
2.3 Microsite probability distribution functions of soil C and soil moisture
The microsite PDFs of soil C substrate and soil moisture were generated from a bivariate truncated log-normal distribution. The PDF for soil C was truncated at 0.001 and 0.15 (g/cm3), respectively. The soil C PDF was distributed with mean equaling the observed soil C value (see Figure S3 for more information on the PDF of soil C). Likewise, the soil moisture PDF was distributed with mean equaling the observed soil moisture value, truncations at 70% and 200% of the observed mean soil moisture values. The spatial heterogeneity of soil C and soil moisture were constrained by optimizing the parameters (standard deviation and/or coefficient of variation) that control the skewness of soil C and soil moisture PDFs by enveloping the bounds reported by Stoyan et al. (2000). If the upper truncation limit of the soil moisture PDF exceeded the soil pore volume, we reset it to 95% of the porosity value. We constructed the microsite PDF as the product of two log-normal distributions of soil C and soil moisture. The PDF was evaluated at 10 × 10 equally spaced quantiles for soil C and soil moisture, respectively.
Here, we focused on spatial heterogeneity across soil microsites at the mm and sub-mm scale. Within stand heterogeneity at the meter scale, such as variation in bulk density and porosity along topographical gradients, is not account for in this study.
2.4 Parameter optimization and uncertainty analysis
We optimized model parameters within a Bayesian Markov chain Monte Carlo (MCMC) framework (see Section S1 for more details on the optimization algorithm). We implemented the MCMC algorithm using mcmc and doParallel packages (Revolution Analytics & Weston, 2015) in the R (version 3.3.2) statistical programming language (R Core Team, 2018). We applied a posterior predictive procedure to estimate the uncertainty of the optimized parameters. We implemented the posterior predictive analyses using the R-INLA package (Lindgren & Rue, 2015; Rue, Martino, & Chopin, 2009). We divided daily-average soil GHG flux measurements into alternative synoptic-scale periods of 10 days, where we used one half of measured GHG fluxes for model calibration and another half for model validation.
2.5 Sensitivity analysis
We evaluated the sensitivity of model parameters using a global variance-based sensitivity analysis and a collinearity (or parameter identifiability) analysis. We implemented a variance-based sensitivity analysis using the R-multisensi package, where a generalized sensitivity index (ranging between 0 and 1, extracted from the first axis of principle component analysis) was used to determine the sensitivity of multiple GHG fluxes to each model parameter value (Bidot, Lamboni, & Monod, 2018). The global sensitivity analysis quantifies the proportion of variability accounted by each of the parameters on model outputs, where a high GSI value indicates that the simulation results are highly sensitive to that parameter (Lamboni, Makowski, Lehuger, Gabrielle, & Monod, 2009).
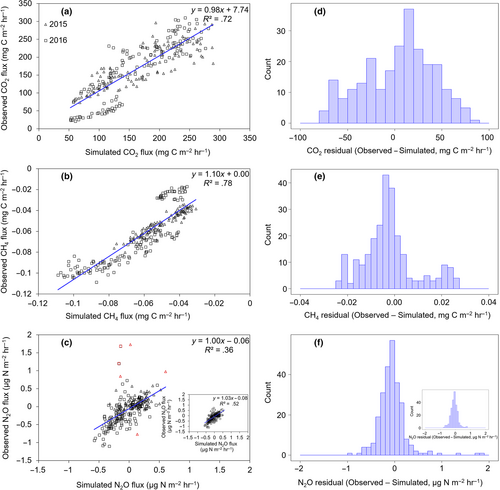
We implemented the collinearity analysis using the collin function of R-FME package, where the collinearity index (CI) was used to determine the linear dependence of model parameters to each other (Brun, Reichert, & Künsch, 2001; Soetaert, 2016; Soetaert & Petzoldt, 2010). In general, higher values of CI indicate increased equifinality (or decreased number of identifiable parameters) of model parameters. One can compensate 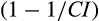 % of the effect of a change in one parameter by modifying the values of other parameters. Hence, CI values can range between 1 (when all terms are orthogonal or all subsets of parameters are identifiable) and infinity (when all terms are linearly dependent, or no single subset of parameters is identifiable). The CI value of 15 is considered as a threshold above which approximate linear dependence of model parameters increases and poor identifiability can be expected (sensu Omlin, Brun, & Reichert, 2001).
% of the effect of a change in one parameter by modifying the values of other parameters. Hence, CI values can range between 1 (when all terms are orthogonal or all subsets of parameters are identifiable) and infinity (when all terms are linearly dependent, or no single subset of parameters is identifiable). The CI value of 15 is considered as a threshold above which approximate linear dependence of model parameters increases and poor identifiability can be expected (sensu Omlin, Brun, & Reichert, 2001).
3 RESULTS
3.1 Seasonality of soil greenhouse gas fluxes
Soil CO2 fluxes followed the typical seasonal trend of soil temperature, where both seasonal average and peak CO2 fluxes were comparable between 2015 (average [min–max]: 171 [73–297] mg CO2-C m−2 hr−1) and 2016 (average [min–max] measurement period: 168 [52–281] mg CO2-C m−2 hr−1; Figure 2). This is due, in part, to the comparable seasonal soil temperature ranges between 2015 (average: 14.4°C, ranged between 8.4 and 18.6°C) and 2016 (average: 13.3°C, ranged between 5.6 and 17.9°C) measurement periods (Figures 2 and 3). Soil CO2 fluxes exponentially increased with soil temperature (R2 = .75; Figure 3a). We also observed a typical bell-shaped relationship between CO2 flux and soil moisture (R2 = .16), with the optimum for CO2 flux at intermediate water contents (Figure 3d). Although the effect of soil moisture on CO2 fluxes was always secondary to soil temperature (Figure S5), the fit with soil moisture was better when it was more limiting in the dry summer of 2016 than the wet summer of 2015 (R2 = .24 and .52 in 2015 and 2016, respectively; Figure S6d).
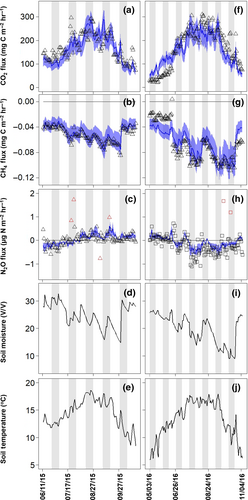
In contrast to CO2 fluxes, soil CH4 fluxes mimicked the seasonal trend of soil moisture for both years (Figure 2b,g). Soil moisture and net CH4 fluxes were positively related (R2 = .70), although the slope of the linear regression line was steeper during 2016 than during 2015 (Figure 3e; Figure S6e). We observed relatively smaller net CH4 oxidation in the spring followed by higher net CH4 oxidation in summer months, and again lower net CH4 oxidation in the autumn. Although seasonal average values were generally similar, the range of CH4 flux values in 2016 (average: −0.07 µg CH4-C m−2 hr−1, min–max range: −0.13 to 0.004 µg CH4-C m−2 hr−1) was wider than in 2015 (average: −0.05 µg CH4-C m−2 hr−1, min–max range: −0.08 to −0.03 µg CH4-C m−2 hr−1).
Unlike CO2 and CH4, the seasonal trend of soil N2O fluxes contrasted between 2015 and 2016 (Figures 2c,h and 3f; Figure S6f). The 2015 growing season was significantly wetter than the 2016 growing season. The cumulative precipitation of the summer months (June 1 to September 30) of 2015 and 2016 was 439 mm and 279 mm, respectively (source: https://www.ncdc.noaa.gov/crn/). Consequently, the average soil moisture was generally higher (24.8 v/v, min–max range: 14.8–32.6 v/v) during the 2015 growing season (measured over June 11 to October 17) than the average soil moisture (19.7 v/v, min–max range: 8.9–27 v/v) during the 2016 growing season (measured over May 3 to November 6; Figures 2d,i and 3f; Figure S6f).
We observed low rates of net N2O consumption during the spring of 2015 when soil moisture was highest, which was followed by mostly near zero net emissions and a few positive emissions throughout the 2015 summer (Figure 2c,d). In contrast, we observed net positive N2O emission during the early spring of 2016 and net N2O consumption throughout most of the 2016 growing season, when soil moisture was minimal (Figure 2h,i). The temperature effect was weak and inconsistent between 2 years (Figure 3c; Figure S6c). On average, we observed small net N2O emission during the 2015 growing season (average: 0.06 µg N2O-N m−2 hr−1, ranged between −0.77 and 1.73 µg N2O-N m−2 hr−1) and net N2O consumption during the 2016 growing season (average: −0.18 µg N2O-N m−2 hr−1, ranged between −1.10 and 1.68 µg N2O-N m−2 hr−1).
3.2 Performance of the DAMM-GHG model
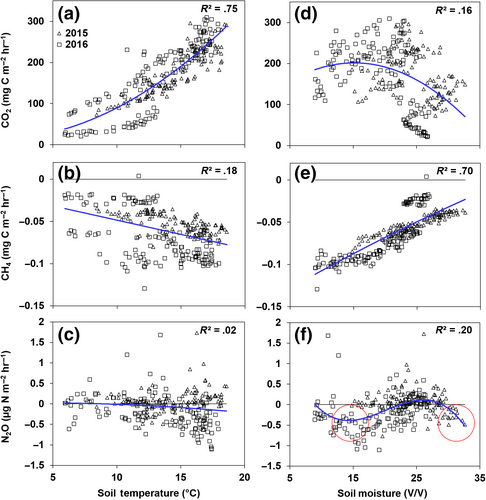
Overall, the model reproduced the seasonal dynamics of soil greenhouse gas fluxes (Figures 2 and 4). The model explained 72% of the variation in soil CO2 fluxes (Figure 4a). Likewise, the 1:1 relation between the observed and simulated soil CH4 fluxes was remarkable (R2 = .78; Figure 4b). The model marginally overestimated CO2 fluxes and underestimated CH4 fluxes during early spring of 2016 (Figure 2f,g).
Soil N2O fluxes were relatively noisier as compared to CO2 and CH4 fluxes with a few outliers in both years (red triangles and squares in Figures 2 and 4, respectively). The model generally explained the dynamics of N2O fluxes (R2 = .36 and .52 with and without outliers, respectively; Figure 4c). The model did not capture the few very low net N2O fluxes observed in the peak season of 2016. Most importantly, the model captured the instances when net atmospheric consumption of CH4 (i.e., net CH4 oxidation) co-occurred with net atmospheric consumption of N2O (i.e., net N2O reduction) within the same soil chamber and at two extremes of the measured soil moisture, during the early wet spring of 2015 and during the driest period of the 2016 growing season (see Figure 2c,h and red circles in Figure 3f).
In general, there was little bias in the relations between the observed and simulated GHG fluxes (slope ranged between 0.98 and 1.10; Figure 4). The 95% CI of the simulated GHGs for all, CO2, CH4, and N2O, were narrow and the model parameter values were generally well constrained. The interquartile ranges in the posterior distributions of all parameters were less than half of their respective prior interquartile ranges (Table 1). The prior interquartile ranges represent the approximate upper and lower bounds of the measured values from the relevant literature.
| Parameter | Description | Unit | Prior range | Posterior range | Source |
|---|---|---|---|---|---|
| For CO2 module | |||||
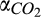
|
Base rate for soil respiration | µmol CO2 L−1 hr−1 | 2 × 1010 (2 × 109–2 × 1011) | 5 × 109 (2 × 109–9 × 109) | Abramoff et al. (2017), Davidson et al. (2018), Sihi et al. (2018) |

|
Temperature sensitivity for soil respiration | kJ/mol | 72 (60–80) | 66 (64–72) | |
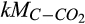
|
Half-saturation constant of C for soil respiration | µmol C/L | 1 (0.1–100) | 0.9 (0.7–1.6) | |
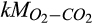
|
Half-saturation constant of O2 for soil respiration | µmol O2/L | 100 (3–300) | 16 (4–38) | |
| Depth | Effective depth | cm | 15 (5–30) | 7 (6–11) | This study |
| Total microsite | Total number of microsites | unitless | 104 (103–105) | 7 × 103 (2 × 103–9 × 103) | This study |
| Soil CSD | Coefficient that determines skewness of soil carbon PDF | unitless | 0.5 (0.1–0.9) | 0.5 (0.1–0.9) | Stoyan et al. (2000) |
| Soil moistureSD | Coefficient that determines skewness of soil moisture PDF | % | 20 (5–30) | 7 (6–12) | Stoyan et al. (2000) |
| For CH4 module | |||||
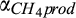
|
Base rate for CH4 production | µmol CH4 L−1 hr−1 | 3 × 105 (3 × 104–3 × 106) | 3 × 105 (2 × 105–6 × 105) | This study |
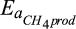
|
Temperature sensitivity for CH4 production | kJ/mol | 100 (50–150) | 74 (68–78) | Nedwell and Watson (1995), Westermann (1993) |
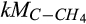
|
Half-saturation constant of C for CH4 production | µmol C/L | 1 (0.1–100) | 1.2 (0.9–2.1) | This study |
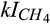
|
Inhibition coefficient of O2 for CH4 production | µmol O2/L | 3 (0.3–4.3) | 0.43 (0.4–0.9) | Arah and Stephen (1998) |
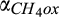
|
Base rate for CH4 oxidation | µmol CH4 L−1 hr−1 | 0.07 (0.007–7) | 0.1 (0.08–2) | Davidson et al. (2001) |
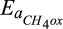
|
Temperature sensitivity for CH4 oxidation | kJ/mol | 30 (10–50) | 34 (32–37) | Crill, Martikainen, Nykanen, and Silvola (1994) |

|
Half-saturation constant of CH4 for CH4 oxidation | µmol CH4/L | 10–2 (10–3 to 10–1) | 0.005 (0.002–0.006) | Davidson et al. (2001) |
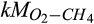
|
Half-saturation constant of O2 for CH4 oxidation | µmol O2/L | 43 (3–300) | 24 (13–33) | Davidson et al. (2001) |
| For N2O module | |||||
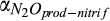
|
Base rate for nitrification | µmol N2O/L | 102 (101–103) | 282 (207–722) | This study |
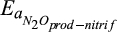
|
Temperature sensitivity for N2O production during nitrification | kJ/mol | 60 (45–75) | 62 (57–67) | Stark (1996), Stark and Firestone (1996) |
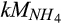
|
Half-saturation constant of 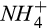 for N2O production for N2O production |
µmol 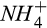 /L /L |
15 (8–22) | 9 (8–10) | Stark and Firestone (1996), Zarnetske, Matsuo, Yamazaki, and Wada (1987) |
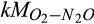
|
Half-saturation constant of O2 for N2O production | µmol O2/L | 100 (9–163) | 36 (15–44) | Bodelier, Libochant, Blom, and Laanbroek (1996), Verstraete and Focht (1977), Zarnetske et al. (1987) |
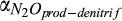
|
Base rate for N2O production | µmol N2O/L | 102 (101–103) | 520 (438–958) | This study |
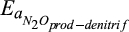
|
Temperature sensitivity for N2O production during denitrification | kJ/mol | 60 (45–75) | 67 (65–71) | Canion et al. (2014), Holtan-Hartwig, Dörsch, and Bakken (2002), Vieten (2008) |
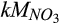
|
Half-saturation constant of 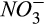 for N2O production for N2O production |
µmol 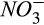 /L /L |
26 (15–57) | 17 (16–19) | Zarnetske et al. (1987) |
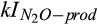
|
Inhibition coefficient of O2 for N2O production | µmol O2/L | 14.3 (4.3–43) | 41 (40–42) | Körner and Zumft (1989), Zarnetske et al. (1987) |

|
Half-saturation constant of C for N2O production and reduction during denitrification | µmol C/L | 1 (0.1–100) | 0.6 (0.3–1) | This study |
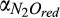
|
Maximum velocity for N2O reduction | µmol N2O/L | 103 (102–104) | 3,413 (1,585–9,583) | This study |
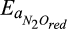
|
Temperature sensitivity for N2O reduction | kJ/mol | 50 (45–75) | 47 (46–47) | Canion et al. (2014), Holtan-Hartwig et al. (2002), Vieten (2008) |
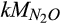
|
Half-saturation constant of N2O for N2O reduction | µmol N2O/L | 0.16 (0.05–0.27) | 0.19 (0.13–0.26) | Holtan-Hartwig et al. (2002), Vieten (2008) |
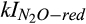
|
Inhibition coefficient of O2 for N2O reduction | µmol O2/L | 7.5 (4.3–20.1) | 19.5 (18.6–19.7) | Körner and Zumft (1989), Vieten (2008) |
Note
- Prior range represents initial (min–max) of prior interquartile range. Posterior range represents median (95% CI) of posterior interquartile range. Units for all base rates, that is, α(s), are in µmol concentration dissolved in water.
- Abbreviation: PDF, probability distribution function.
The effective depth in the DAMM-GHG model was optimized to a median value of 7 cm (min–max range: 6–11 cm; Table 1), indicating that most of the important processes affecting the net GHG fluxes that we measured with chambers were occurring within the topsoil horizons at this site. The number of microsites within the 0.07 m2 chamber footprint was optimized to a median value of 7,000 (min–max range: 2,000–9,000; Table 1), indicating that the simulated microsites were about 3.6 mm in diameter, which could include macroaggregates and clusters of fine roots and pockets of organic debris.
3.3 Sensitivity analysis
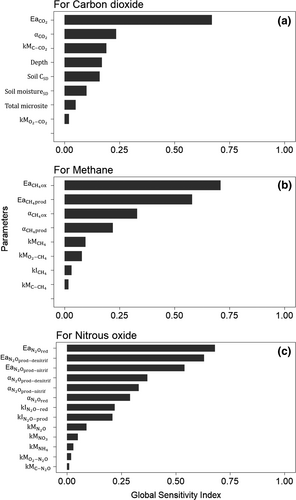
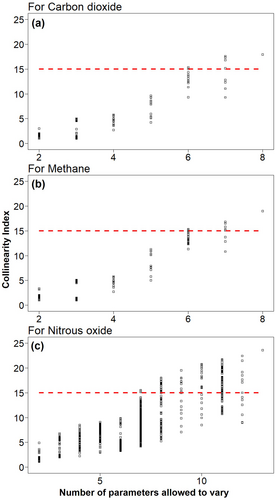
Soil moisture primarily (and soil temperature secondarily) controlled the microsite PDFs of production, consumption, and diffusion processes of CO2, CH4, and N2O. The net flux is the net effect of production, consumption, and diffusion of individual gases (Figure 5; Figure S10). Of all parameters, the most sensitive ones were those that control the Vmax terms in the Arrhenius equation (Ea and α) for production and consumption of individual GHGs, followed by the half-saturation constants (kMs) and O2 inhibition coefficients (kIs) for each process (Figure 6). The linear dependence of the DAMM-GHG model parameters was generally low and was usually below the threshold of 15 (with a few exceptions) identified for potential equifinality issues (Figure 7).

4 DISCUSSION
Our goal is a novel integration of measurement and modeling of three key greenhouse gases to improve understanding of and modeling capacity for interactions of belowground temperature, moisture, and substrate supply that control the net soil emissions of CO2, CH4, and N2O. To this end, we built upon the DAMM model, which mechanistically simulates soil Rh using Arrhenius equations, diffusion functions, and Michaelis–Menten enzyme kinetics (Davidson et al., 2012, 2014). Our framework of the DAMM-GHG model is unique in that it represents the simultaneous production and consumption of all three GHGs within the same soil biophysical framework using microsite PDFs. Below we discuss the performance of the DAMM-GHG model and the utility of the microsite PDFs in reproducing the spatial and temporal dynamics of observed CO2, CH4, and N2O fluxes within a multiple constraint framework.
4.1 Microsite representation captures co-occurrence of methane oxidation and nitrous oxide reduction
Consumption of atmospheric N2O via classical denitrification should occur only under reducing conditions. Yet, we have observed net uptake of atmospheric CH4 (oxidation) and uptake of atmospheric N2O (reduction) simultaneously in well-drained soils of Howland forest under both low and high soil moisture levels. With the advent of high frequency and high sensitivity flux measurement technology, we can be confident that these modest uptake rates of both CH4 and N2O are significantly different from zero and are not measurement errors or artifacts (Figures 2 and 4; also see Figure S4). These seemingly contradictory observations have been qualitatively explained by describing diffusional constraints of gas transport as follows: both CH4 and N2O can diffuse into well-drained soils; the CH4 is oxidized at microsites where O2 is abundant; while N2O is reduced at other microsites where N2O is present and Rh is sufficiently rapid to consume O2. Here, we demonstrate that this qualitative explanation can be expressed in a mathematically consistent biophysical process model that is numerically consistent with simultaneously measured fluxes of these gases.
The area under a soil chamber was partitioned according to a bivariate log-normal PDF of soil C and moisture across a range of microsites, which leads to a PDF of CO2 production and O2 consumption among microsites. The resulting broad range of microsite O2 concentrations determines the PDF of microsites that produce or consume CH4 and N2O according to Michaelis–Menten and Arrhenius functions for each process (Figure 1; Figure S1). Concentrations of below ambient N2O (hot spots of N2O reduction) occur in microsites with simulated high C and high moisture. Net consumption and production of CH4 and N2O are simulated within a chamber as the average of all soil microsite simulations. To demonstrate that it is numerically feasible for microsites of N2O reduction and CH4 oxidation to co-occur under a single chamber, we discuss three different scenarios where mean soil moisture levels cover the envelope of observed soil moisture in our study area (Figure 5).
Of the two growing seasons, we measured highest bulk soil moisture (32.6 v/v) on June 29 (DOY 180), 2015. Consequently, microsite PDFs of soil moisture ranged from 23.7 v/v to as high as 47.7 v/v (solid line in Figure 5b). Microsites with high soil moisture limited diffusion of gaseous O2 through air-filled pore space. Simultaneously, soils had warmed up enough during the late spring of 2015 for soil respiration to exceed 100 mg CO2-C m−2 hr−1, which created significant O2 demand in microsites with high soil C. Relatively high soil respiration along with limited O2 diffusion resulted in a large fraction of total soil microsites with low O2 concentrations (solid line in Figure 5d). Production of N2O was high in microsites with high soil C. However, reducing environments favored N2O reduction more than N2O production in microsites with low O2 concentrations. Together, the PDFs of soil microsites resulted in a modest net negative mean flux of N2O (solid line in Figure 5l). Classical theories of biological denitrification processes fit with our observations of net negative fluxes of N2O under conditions of high soil moisture (and soil C) when enzymatic reduction of N2O to N2 under reducing environment outcompete N2O production rates, especially in nitrogen-limited systems like our field site (Davidson, Keller, Erickson, Verchot, & Veldkamp, 2000; Davidson et al., 1993; Firestone & Davidson, 1989). Although N2O reduction slightly exceeded N2O production under these conditions, net uptake rates of atmospheric N2O were low, because diffusion of atmospheric N2O into the soil, while occurring and thus supporting some uptake, was also limited by high water-filled pore space.
The diffusion of atmospheric N2O into the soil increased during the drier 2016 summer, thus enabling somewhat larger net uptake of atmospheric N2O. The observed soil moisture content of 18.2 v/v on July 30 (DOY 212), 2016, approximately represents the first quantile of observed soil moisture across 2015 and 2016 growing seasons. Rates of N2O production during nitrification and denitrification were low in a large majority of microsites due to the oxygen inhibition effects as well as the diffusional constraints of soil C, ammonium, and nitrate substrates at low soil moisture. However, greater diffusion of atmospheric N2O to soil microsites also increased the microsite concentrations of N2O (dotted line in Figure 5j), including a small fraction of microsites with sufficiently low O2 concentrations to not fully inhibit N2O reduction (i.e., the simulated O2 was near the kI for N2O reduction (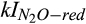 ) in approximately 10% of total microsites, resulting in net negative flux of N2O (dotted line in Figure 5d; Table 1). Our observation of a net soil sink of atmospheric N2O during summer drying events match with reports from other natural and managed ecosystems, ranging from tropical to temperate climates, where net uptake of atmospheric N2O has been measured when mean bulk soil moisture was drier than would normally be expected for N2O reduction (Donoso, Santana, & Sanhueza, 1993; Flechard, Neftel, Jocher, Ammann, & Fuhrer, 2005; Goldberg & Gebauer, 2009; Verchot et al., 2000; Yamulki, Goulding, Webster, & Harrison, 1995). In this case, however, we can demonstrate quantitatively that reducing conditions in only about 10% of the microsites was sufficient to enable net uptake of atmospheric N2O.
) in approximately 10% of total microsites, resulting in net negative flux of N2O (dotted line in Figure 5d; Table 1). Our observation of a net soil sink of atmospheric N2O during summer drying events match with reports from other natural and managed ecosystems, ranging from tropical to temperate climates, where net uptake of atmospheric N2O has been measured when mean bulk soil moisture was drier than would normally be expected for N2O reduction (Donoso, Santana, & Sanhueza, 1993; Flechard, Neftel, Jocher, Ammann, & Fuhrer, 2005; Goldberg & Gebauer, 2009; Verchot et al., 2000; Yamulki, Goulding, Webster, & Harrison, 1995). In this case, however, we can demonstrate quantitatively that reducing conditions in only about 10% of the microsites was sufficient to enable net uptake of atmospheric N2O.
In contrast to the above two examples, intermediate soil moisture conditions are favorable for production to exceed consumption, resulting in modest net emissions of N2O from soil to the atmosphere. Within this context, observed soil moisture content of 25.4 v/v on July 10, 2016 (DOY 192; dashed lines in Figure 5), approximately represents the third quantile of observed soil moisture across 2015 and 2016 growing seasons (Figure 5b). As expected, N2O production was greatest at this intermediate soil moisture (Figure 5j), especially in microsites with high soil C. Because N2O production was much higher than the very low N2O reduction rates (Figure 5k) in a sufficiently large number of total soil microsites, a net positive mean N2O flux resulted (Figure 5l).
Previous studies indicated that N2O production during biological nitrification and denitrification often peak at 50%–80% of water-filled pore space (Davidson, 1991; Metivier, Pattey, & Grant, 2009), when soil moisture may be sufficiently high such that nitrate and nitrite are more available than O2 as the alternate elector acceptor in many microsites, but the soil O2 content is still high enough to mostly inhibit the reduction of N2O to N2. This is the basis of the soil moisture function of the conceptual hole-in-the-pipe model (Firestone & Davidson, 1989). This relationship between soil moisture and N2O production is often represented in models as an empirical statistical algorithm, such as a polynomial or similar function (e.g., Del Grosso et al., 2001; Potter, Matson, Vitousek, & Davidson, 1996). In contrast, the responses to soil moisture in the DAMM-GHG model produce the response pattern across simulated microsites (Figure S7) predicted by the conceptual hole-in-the-pipe model as an emergent property of the role of O2 as substrate (for nitrification, see Figure S1) or inhibitor, as represented by different kI values (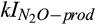 and
and 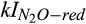 ) used in DAMM mechanistic functions (Table 1).
) used in DAMM mechanistic functions (Table 1).
For CH4, the microsite PDFs of production, consumption, and net emission were relatively straightforward. Methane production was high in a relatively few numbers of microsites with high soil moisture (and soil C). In contrast, CH4 oxidation was high in the majority of microsites, which had low soil moisture, as the diffusion of both substrates (O2 and CH4) increased with decreasing soil moisture. Note that CH4 production was several orders of magnitude lower than CH4 oxidation across the simulated range of microsite moisture contents in our study, mainly due to significant oxygen inhibition. Therefore, microsite PDFs of CH4 oxidation primarily dominated the net CH4 emission, where net CH4 emission linearly decreased with decreasing soil moisture (Figure 5e–h).
Taken together, these results demonstrate that representing production, consumption, and diffusion processes as a function of soil microsite PDFs can neatly encapsulate the factors affecting emissions of CO2, CH4, and N2O in field studies and their underlying mechanisms. We also did a comparison of the model performance to a conventional framework, where we kept identical soil C and soil moisture values, set to the average values observed for the bulk soil, across all microsites. Although the performance of the model without microsite PDF was comparable to the one with microsite PDF for CO2, model performance for CH4 and N2O was strongly affected by microsite variability (Figures S8 and S9). The model without microsite PDF simulated less uptake of CH4 overall, had larger than observed peaks and valleys during in wet-up and dry-down events, and had more biased residuals (Figures S8b,g and S9b,e). For N2O, the model with PDF representation of microsite variation also had an overall better fit to the observations and less biased residuals (Figures S8c,h and S9c,f).
The model–data fusion algorithm we used tends to reduce the overall model–data mismatch for the entire measurement window, and so it is not surprising that there are periods within that window where simulations do not match observations as well, such as the CO2 and CH4 fluxes of spring 2016 (Figure 2). This may also be due to other factors not included in the DAMM-GHG model, such as impacts of spring freeze–thaw cycles on C availability or phenology of root exudates. Additionally, the lower fraction of observed variability of N2O fluxes accounted for by the model, compared to CO2 and CH4 fluxes, can be attributed to: (a) the low signal-to-noise ratio inherent to very low N2O fluxes; and (b) the increased number and complexity of interactions of substrates (and inhibitors) for production (e.g., C, O2, 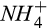 , and
, and 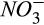 ) and consumption (e.g., C, O2, and N2O) of N2O during nitrification and denitrification that are represented numerically in the model with additional parameters (Figures 2 and 4). We further discussed how these potential interacting processes might have increased the covariation of parameters related to N2O dynamics than those related to CO2 and CH4 dynamics (see Section 4.3).
) and consumption (e.g., C, O2, and N2O) of N2O during nitrification and denitrification that are represented numerically in the model with additional parameters (Figures 2 and 4). We further discussed how these potential interacting processes might have increased the covariation of parameters related to N2O dynamics than those related to CO2 and CH4 dynamics (see Section 4.3).
4.2 Sensitivity analysis
4.2.1 Sensitivity of predicted greenhouse gas fluxes to model parameters
Sensitivity indices indicated that the parameters representing the Vmax terms in the Arrhenius equation (α and Ea) for production and consumption of each gas were the most influential for all three GHGs (Figure 6a–c), which is in line with other reports (Abramoff, Davidson, & Finzi, 2017; Zarnetske, Haggerty, Wondzell, Bokil, & González-Pinzón, 2012). Sensitivity of GHG fluxes to the parameters representing Michaelis–Menten equations was secondary to those of the α(s) and Ea(s), where the individual ranking was associated with the importance of controlling drivers. Following α(s) and Ea(s), some of the half-saturation constants, that is, kM(s), were more important than others. For example, relatively higher sensitivity indices of the half-saturation constants of CH4 ( ) and O2 (
) and O2 (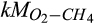 ) for CH4 oxidation as compared to the half-saturation constants of C (
) for CH4 oxidation as compared to the half-saturation constants of C (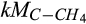 ) and inhibition coefficient of O2 (
) and inhibition coefficient of O2 (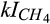 ) for CH4 production can be explained by the dominant role of CH4 oxidation in controlling net CH4 emissions in our study. The inhibition coefficients of O2 for N2O reduction (
) for CH4 production can be explained by the dominant role of CH4 oxidation in controlling net CH4 emissions in our study. The inhibition coefficients of O2 for N2O reduction (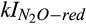 ) and N2O production (
) and N2O production (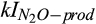 ), along with the half-saturation constant of N2O for N2O reduction (
), along with the half-saturation constant of N2O for N2O reduction (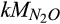 ), had relatively higher sensitivity indices than those for the half-saturation constant of ammonium (
), had relatively higher sensitivity indices than those for the half-saturation constant of ammonium (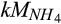 ) and O2 (
) and O2 (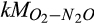 ) during nitrification and nitrate (
) during nitrification and nitrate (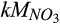 ) and C
) and C  during denitrification, respectively. These results indicate the greater importance of reducing conditions and the diffusive supply of N2O in controlling net N2O emission at our site than either the concentrations of
during denitrification, respectively. These results indicate the greater importance of reducing conditions and the diffusive supply of N2O in controlling net N2O emission at our site than either the concentrations of 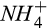 and O2 substrates for nitrification or
and O2 substrates for nitrification or 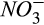 and C substrates for denitrification. This result may be particular to our site where
and C substrates for denitrification. This result may be particular to our site where 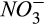 is uniformly low and the seasonal trend of
is uniformly low and the seasonal trend of 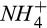 is much less dynamic than that of soil moisture (Fernandez et al., 1995). We speculate that
is much less dynamic than that of soil moisture (Fernandez et al., 1995). We speculate that 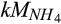 and
and  might be more commonly important in agricultural soils, where large temporal variations in
might be more commonly important in agricultural soils, where large temporal variations in 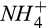 and
and 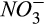 are expected depending on the timing of fertilization and crop uptake.
are expected depending on the timing of fertilization and crop uptake.
4.2.2 Sensitivity of predicted greenhouse gas fluxes to model drivers
Soil moisture primarily (and soil temperature secondarily) controlled the skewness of the microsite PDFs of production, consumption, and diffusion processes of each gas (Figure S10). Within this context, it is important to note that even though the parameters representing the Vmax terms in the Arrhenius equation (Ea and α) had higher sensitivity indices than the Michaelis–Menten parameters that represent the influence of soil moisture (Figure 6a–c), most of the temporal variations in CH4 and N2O fluxes were nevertheless explained by soil moisture rather than temperature. The correlation matrix in Figure S5 also indicates that soil moisture, rather than soil temperature, controlled the temporal variation of CH4 and N2O fluxes. In other words, if the Ea value is changed, the average simulated flux for the entire time period increases or decreases significantly, but the within-season variation in CH4 and N2O fluxes is still dominantly influenced by variation in soil moisture (Figures S6 and S10).
4.3 Collinearity analysis
As expected, the CI increases as the number of variable parameters increases (Figure 7). Given the parsimonious model structure, we had few problems of identifiability of the processes for CO2 and CH4 module, and the most parameter combinations remain below the threshold value of 15 (Brun, Kühni, Siegrist, Gujer, & Reichert, 2002; Omlin et al., 2001). However, we do have some parameter combinations with CI > 15 for the N2O module, due to probable ambiguity of whether N2O fluxes are affected more by production via nitrification (affected by 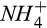 substrate), production via denitrification (affected by
substrate), production via denitrification (affected by 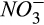 substrates), or consumption of N2O (affected by N2O diffusion). Trade-offs of processes within models can account for inflation of CI values (Keenan, Carbone, Reichstein, & Richardson, 2011; Richardson et al., 2010), which is likely the case for the N2O module relative to the CO2 and CH4 modules. Overall, however, collinearity analysis indicates that the chances of having equifinality issues characterized by biologically improbable process representations were generally low in the DAMM-GHG model.
substrates), or consumption of N2O (affected by N2O diffusion). Trade-offs of processes within models can account for inflation of CI values (Keenan, Carbone, Reichstein, & Richardson, 2011; Richardson et al., 2010), which is likely the case for the N2O module relative to the CO2 and CH4 modules. Overall, however, collinearity analysis indicates that the chances of having equifinality issues characterized by biologically improbable process representations were generally low in the DAMM-GHG model.
We believe that this success is largely due to the multiple constraints imposed by simultaneously modeling data streams of three different gases, which enabled us to capture the influence of temporally and spatially varying drivers on GHG fluxes (Myrgiotis, Williams, Topp, & Rees, 2018). For example, when simulating only CH4 flux, a better fit of the model to the data might be achieved by adjusting either the Michaelis–Menten parameters or the diffusion parameters, but it may be impossible to know which the “correct” adjustment is. However, if N2O and CO2 are also being simultaneously simulated, then adjusting the diffusion parameters will affect simulations of all three gases, whereas adjusting the Michaelis–Menten parameters for CH4 oxidation should have little effect on the other two gases. Hence, the additional constraints help identify which model parameterizations are consistent with all three data streams of flux measurements.
4.4 Microsite probability distribution functions permit model parsimony
Simulating a 3-D array of soil aggregates or pore networks (Arah & Vinten, 1995; Ebrahimi & Or, 2014; Yan et al., 2016) is another approach for representing spatial heterogeneity of soil matrix in biogeochemical models. However, explicit representation of soil spatial variability requires detailed information on soil structure, involving high-throughput instrumentations such as X-ray CT scan (see Carducci, Zinn, Rossoni, Heck, & Oliveira, 2017) and may require greater computational power than our PDF approach. Because of the limited measurements on the spatial variability of soil aggregates (or pores) at a plot scale, let alone at larger scales, and because of the increased computational complexity in spatially explicit model structures, scaling up of 3-D soil aggregate (or pore network) models to the ecosystem models and ESMs is still challenging.
Statistically representing microsite variation as PDFs in the DAMM-GHG model offers a relatively computationally efficient, yet mechanistically consistent, alternative way of simulating soil heterogeneity and maintaining model parsimony, as in the original DAMM model (Davidson et al., 2012, 2014; Sihi et al., 2018). We believe that our framework could be used to simulate fluxes of GHGs from other natural and managed systems as well as be scaled up to ecosystem models and ESMs.
4.5 Opportunities for future improvement of the DAMM-GHG model
We represented all microsite-scale processes by optimizing an equivalent depth for Rh, where most of the biological reactions appear to happen in the soil of this study site (posterior range: 6–11 cm) and fixed that depth for simulating processes related to production and consumption of CH4 and N2O. This simplification allowed us to use unitless diffusion constants for gaseous and dissolved substrates and to avoid needing to know exact diffusion path lengths (see Davidson et al., 2012 for details). Exploring heterogeneity of diffusivity within and among soil horizons could be an appropriate next step.
Including more complex models of gas diffusion that includes variable diffusivity between intra-aggregate and inter-aggregate pore spaces may be more appropriate for aggregated media like soil (Millington & Shearer, 1971; Resurreccion et al., 2010). Representing soil microsite PDFs in more than one vertically stratified soil horizon by differentiating between the organic and various mineral horizons may be needed for application to other sites (e.g., wetland with a seasonally variable depth to the water table), such that transport of gases between soil horizons and across soil–air boundary can be estimated using Fick's law. Measured vertical concentration profiles of soil gases could serve as additional data constraints for soil gas concentration profiles that become emergent simulated properties of this modeling approach. It would also be useful to have a data stream of heterogeneity of O2 or redox potentials across microsites, but that would require new generations of microprobes.
Additionally, techniques that disentangle gross production and gross consumption rates of CH4 and N2O under field conditions could increase the predictive power of the dynamics of soil GHGs fluxes. For example, Chanton, Powelson, Abichou, and Hater (2008) reported that measuring stable carbon isotope of emitted CH4 (13CH4) is a feasible way to quantify gross CH4 oxidation in situ. Likewise, Wen et al. (2016) demonstrated that 15N2O pool dilution method can be effective to measure atmospheric N2O uptake in soil under field conditions. In situ quantification of microbial activities pertaining to gross production and consumption of CH4 and N2O can also be pursued following the gas push-pull method (Urmann, Gonzalez-Gil, Schroth, Hofer, & Zeyer, 2005). Quantifying gross nitrogen transformations using stable isotope tracing could help constrain the sources of N2O emissions (Morse & Bernhardt, 2013; Müller, Rütting, Kattge, Laughlin, & Stevens, 2007; Myrold & Tiedje, 1986).
In addition to nitrification and biological denitrification, other bacterial (Jensen & Burris, 1986; Yamazaki, Yoshida, Wada, & Matsuo, 1987) and fungal (Hayatsu, Tago, & Saito, 2008; Shoun, Kim, Uchiyama, & Sugiyama, 1992) contributions, as well as abiotic (Davidson, Chorover, & Dail, 2003; Vieten, 2008) sinks of N2O in soil could be explored if warranted. Adding other controlling factors, such as pH effects, temporal dynamics of enzyme synthesis, and root exudation, could improve model performance for some sites (Butterbach-Bahl et al., 2013; Zheng & Doskey, 2015). In all of these cases, however, the potential additional explanatory value of more parameters and model complexity must be balanced with the availability of data to constrain them and with the advantages of model structure parsimony.
5 CONCLUSIONS
Representing microsite heterogeneity as PDFs related to predictive processes offers a new approach for numerical representation of methanogenesis, methane oxidation, nitrification, and denitrification and other spatially and temporally variable microbial processes in soil. Our ability to accurately measure and skillfully model rates of these processes has been hampered by highly variable soil microsite conditions, which are difficult to measure and simulate, but our use of PDFs to represent that variability offers a promising and computationally efficient approach. In addition, by measuring and modeling all three greenhouse gases (CO2, CH4, and N2O), we have mechanistically and quantitatively explained the apparent paradox of observed simultaneous aerobic respiration that produces CO2, CH4 uptake (oxidation), CH4 production, and N2O uptake (reduction) in the same soil profile. Skillful representations of multiple ecologically relevant processes increase confidence of getting the right answers for the right reasons. This relatively parsimonious process modeling framework has the potential to be implemented within ecosystem models and ESMs to better capture the dynamics of soil-based greenhouse gases at landscape, regional, and global scales.
ACKNOWLEDGEMENTS
This work was supported by the USDA NIFA award # 2014-67003-22073. Research activities at the Howland Forest are supported by the USDA Forest Service's Northern Research Station and the US Department of Energy's BER (Office of Science) Program. We thank Dr. Andrew D. Richardson for facilitating our access to the Odyssey cluster supported by the FAS Division of Science at the Harvard University, which we used for computational purposes. All data used in this paper are available through Richardson et al. (2019). R scripts used for this modeling work are made available as a GitHub repository (https://github.com/dsihi/DAMM-GHG).




