Prediction: Coveted, Yet Forsaken? Introducing a Cross-Validated Predictive Ability Test in Partial Least Squares Path Modeling
Beginning August 2020, Dr. Sharma will be on the faculty of Information Systems, Statistics and Management Science in the University of Alabama's Culverhouse College of Business. He can be reached at [email protected]
[Article updated on June 8, 2020 after first online publication: Additional affiliation information inserted for Dr. Pratyush Nidhi Sharma.]
ABSTRACT
Management researchers often develop theories and policies that are forward-looking. The prospective outlook of predictive modeling, where a model predicts unseen or new data, can complement the retrospective nature of causal-explanatory modeling that dominates the field. Partial least squares (PLS) path modeling is an excellent tool for building theories that offer both explanation and prediction. A limitation of PLS, however, is the lack of a statistical test to assess whether a proposed or alternative theoretical model offers significantly better out-of-sample predictive power than a benchmark or an established model. Such an assessment of predictive power is essential for theory development and validation, and for selecting a model on which to base managerial and policy decisions. We introduce the cross-validated predictive ability test (CVPAT) to conduct a pairwise comparison of predictive power of competing models, and substantiate its performance via multiple Monte Carlo studies. We propose a stepwise predictive model comparison procedure to guide researchers, and demonstrate CVPAT's practical utility using the well-known American Customer Satisfaction Index (ACSI) model.
INTRODUCTION
Management and social science disciplines have historically placed substantial emphasis on theory and understanding, where prediction devoid of a causal explanation is considered suspect and attributed to chance correlation (Douglas, 2009; Tsang, 2009). However, deprived of the ability to predict, a causal explanation becomes unverifiable and uncontradictable, and so loses its practical relevance (Shmueli, 2010). In his seminal treatise on the philosophy of science, Conjectures and Refutations, Popper (1962) posited that prediction is the primary criterion for evaluating falsifiability and that all explanatory theories must “rise and fall based on their objective predictions” (Shugan, 2009, p. 994). Thus, a successful marriage between explanation and prediction lends authority to our knowledge of a system (Dubin, 1969). This is the fundamental quest of science.
Although explanation and prediction are philosophically compatible, in practice they are often not treated as such (Yarkoni & Westfall, 2017). For example, the supervised machine-learning models utilized in data-driven fields such as artificial intelligence, computational linguistics, and bioinformatics have traditionally focused solely on predictive assessments. Only recently have researchers started to explore how to draw causal inferences from these predictive models (Athey, 2017; Chernozhukov et al., 2018; Wager & Athey, 2018). In contrast, the explanation-oriented models typically used in the management and social science disciplines often ignore predictive power assessments using established methods such as cross-validation (Shmueli & Koppius, 2011; Yarkoni & Westfall, 2017). A possible reason for this singular focus is that a large segment of theory-driven management and social science research does not rely on observational data as is commonly processed by machine-learning techniques. Instead, researchers frequently deal with latent constructs such as individuals’ attitudes, intentions, and perceptions that are analyzed by using complex regression-based techniques.
Researchers frequently bemoan the lack of prediction in management and social science research, calling for the routine use of methods that facilitate estimating an explanatory model's predictive power (e.g., Shmueli & Koppius, 2011; Hofman, Sharma, & Watts, 2017; Hair, Sarstedt, & Ringle, 2019b). One particularly useful technique in this respect is the composite-based partial least squares path modeling (PLS), which has gained substantial popularity in the last few years in management research (e.g., Hair, Sarstedt, Pieper, & Ringle, 2012a; Ringle, Sarstedt, Mitchell, & Gudergan, 2019) and numerous other fields (e.g., Kaufmann & Gaeckler, 2015; Nitzl, 2016). PLS is considered well-suited to create and evaluate explanatory-predictive theories due to its predictive stance coupled with its explanatory strengths (Jöreskog & Wold, 1982; Sarstedt, Ringle, & Hair, 2017). For example, Becker, Rai, and Rigdon (2013) and Evermann and Tate (2016) show that PLS has high predictive accuracy across a broad range of conditions. Related developments have expanded the scope of PLS's predictive abilities by introducing a framework to assess out-of-sample predictive power (Shmueli, Ray, Velasquez Estrada, & Chatla, 2016), error-based out-of-sample metrics (Becker et al., 2013; Evermann & Tate, 2016), and information theory-based metrics for prediction-oriented model selection (Sharma, Sarstedt, Shmueli, Kim, & Thiele, 2019a; Sharma, Shmueli, Sarstedt, Danks, & Ray, 2019b).
Despite these promising developments, a weakness in the PLS armory is the lack of a statistical test to compare whether a proposed or alternative theoretical model (henceforth the AM) offers significantly better out-of-sample predictive power than a theoretically derived benchmark or established model (henceforth the EM). This is a critical requirement if PLS is to fulfill its promise as a predictive tool for theory development, because expert predictions in the social sciences are often unreliable due to their reliance on causal-explanatory models based solely on in-sample assessments (Silver, 2012; Gonzalez, 2015). The ability to conduct such assessments to improve the predictive relevance of models is crucial, not only for theory development and validation, but also for selecting models on which to base managerial and policy decisions (Shmueli et al., 2016; Hofman et al., 2017).
Our primary contribution is to fill this research gap by introducing the cross-validated predictive ability test (CVPAT) in PLS. The test enables a pairwise comparison between theoretically derived competing models, and selecting the model with the highest predictive power based on a prespecified statistical significance level, to enhance the theoretical and managerial relevance of PLS studies. Due to its reliance on cross-validation, CVPAT helps reduce generalization error, thereby increasing the likelihood that the associated inferences will apply well to other datasets drawn from the same population (Markatou, Tian, Biswas, & Hripcsak, 2005). This characteristic is particularly useful for decision makers who often face binary choices while designing and reviewing policies, and who want to know whether they will be effective in other situations as well (Snow & Phillips,2007).
In the following, we discuss the concerns with the current predictive model assessment tools in PLS, and introduce CVPAT. Next, we demonstrate CVPAT's ability to select the best model for prediction purposes by assessing its statistical power and Type I error probability using multiple Monte Carlo studies. We then introduce a stepwise predictive model comparison procedure to guide researchers, and illustrate its practical utility using the well-known American Customer Satisfaction Index (ACSI) model. Finally, we discuss potential misconceptions that may arise in the application of the CVPAT, and provide guidance to researchers to support its adoption.
EXPLANATION SANS PREDICTION: CONCERNS REGARDING THE CURRENT PLS PREDICTION TOOLKIT
In recent years, PLS has become a popular tool in management and the social sciences to model relationships among latent and manifest variables (e.g., Hair et al., 2012a; Kaufmann & Gaeckler, 2015; Nitzl, 2016).1 Several models relevant to the broader management field, such as the ACSI (Fornell, Johnson, Anderson, Cha, & Bryant, 1996) and the unified theory of acceptance and use of technology acceptance model (UTAUT; Venkatesh, Morris, Davis, & Davis, 2003), have relied almost exclusively on PLS in their development. PLS is well-suited for building theories that offer both explanation and prediction, because of its empirical strengths that bridge both explanatory and predictive goals (Shmueli et al., 2016).2 Unlike supervised machine-learning techniques—such as artificial neural networks, which are considered “black boxes” because they offer good predictions but no causal interpretability (Yarkoni & Westfall, 2017)—PLS is a transparent technique. It enables interpretability in the form of a diagram depicting causal linkages between variables based on theory so that researchers can fine-tune the actual theoretical underpinnings of predictions (Shmueli et al., 2016; Sarstedt et al., 2017).
Methodological developments in PLS have focused on developing its causal-explanatory strengths by proposing several goodness-of-fit measures. Examples include the standardized root mean square residual (SRMR) and the exact fit test (Henseler et al., 2014). Besides the conceptual concerns regarding their usefulness in PLS (e.g., Lohmöller, 1989; Hair et al., 2019b), the goodness-of-fit criteria are usually in-sample measures oriented toward assessing a model's explanatory power and specification, but not its out-of-sample predictive power (Shmueli et al., 2016; Sharma, Pohlig, & Kim, 2017). As a result, these measures provide no guarantee regarding how well the model will fit another dataset, nor regarding how generalizable the inferences and policy recommendations will be to other, similar contexts (Petter, 2018). In contrast to causal-explanatory model evaluation where the focus is on parameter estimation and model fit (Fornell & Bookstein, 1982), predictive model evaluation relies on the use of cross-validation and out-of-sample error metrics (Shmueli & Koppius, 2011).
Research on PLS has only recently begun to follow calls to focus on its strength as a predictive technique (e.g., Rigdon, 2012, 2014) and propose metrics to assess predictive relevance (Shmueli et al., 2016; Shmueli et al., 2019). For example, Sharma et al. (2019b) introduced several information theory-based model selection criteria to PLS, such as the Akaike information criterion (AIC) and the Bayesian information criterion (BIC), to enable model comparisons by balancing model fit and complexity (i.e., the bias-variance trade-off). These criteria strengthen PLS's repertoire by allowing researchers to select correctly specified models with low prediction error. Their in-sample nature, however, means that researchers cannot assess the actual out-of-sample performance of models on unseen data.
Thus far, the Stone–Geisser criterion (Q²), which is based on the blindfolding procedure, has been the only (quasi) out-of-sample test criterion with which to assess a model's predictive relevance in PLS (Chin, 1998; Hair, Hult, Ringle, & Sarstedt, 2017a). Shmueli et al. (2016) note, however, that the Q² has several major limitations, namely (1) it does not draw a clear distinction between the training and the holdout sets3 (i.e., it is not a “true” out-of-sample metric), (2) it is an ad hoc measure, which provides no clear cutoffs for model comparisons, and (3) its imputation steps do not take heterogeneity in prediction errors into account. As a remedy, they introduced the PLSpredict procedure, which provides a framework within which to assess a PLS path model's predictive quality via true out-of-sample metrics such as the root mean square error (RMSE) and the mean absolute error (MAE).
Although PLSpredict improves PLS's prediction-oriented model assessment capabilities considerably, the approach does not offer an overall inferential test to assess whether the AM's predictive capabilities are significantly better than the EM's. Deprived of this capability, researchers are left in the dark regarding the generalizability of their models to other samples and contexts, and incapable of successfully utilizing the strengths of predictive modeling in the management and social science disciplines (Shmueli & Koppius, 2011; Hofman et al., 2017). Addressing this critical concern, we propose CVPAT to enable such comparisons, and substantiate its performance via several Monte Carlo studies.
CVPAT FOR PREDICTIVE MODEL COMPARISON
CVPAT is designed to conduct a pairwise comparison between two theoretically derived models for their ability to predict the indicators of all the dependent latent variables simultaneously. For practical utility and ease in decision-making, the test determines whether the AM has a significantly better predictive accuracy than the EM (or not) at a prespecified significance level (e.g., α = .05). To quantify the out-of-sample prediction errors, CVPAT relies on k-fold cross-validation (Stone, 1974), which is a widely used procedure in modern machine-learning prediction methods, but which Shmueli et al. (2016) have only recently introduced in the PLS context. Cross-validation seeks to assess a model's out-of-sample predictive power or generalization error by recycling and splitting the sample into training and holdout sets k-times (Hastie, Tibshirani, & Friedman, 2009). For representative samples, the cross-validated generalization error estimate will typically be very close to the model's true out-of-sample performance (Yarkoni & Westfall, 2017). As such, cross-validation enables the assessment of a model's generalization performance, and acts as a safeguard against overfitting and underfitting, particularly in situations where researchers build complex models using relatively small datasets—as is often the case in PLS.
CVPAT randomly splits the dataset into a specific number of groups or folds (e.g., 10-folds) and iterates through all the folds. In the first iteration, it reserves the first fold as an independent holdout set and estimates the model on the remaining observations, which act as the training set. Using the training parameter estimates, the output variables of the first fold are predicted by their input variables. The out-of-sample prediction error is the difference between the predicted value of the output variables and their actual values. The procedure is repeated for each fold to generate the out-of-sample prediction errors for each observation in the dataset. Online Supplement OS.2 presents a detailed description of the CVPAT algorithm.
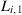 and
and 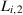 denote the individual losses for the EM and the AM, respectively; then the average loss difference
denote the individual losses for the EM and the AM, respectively; then the average loss difference 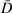 is calculated as
is calculated as
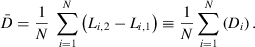 (1)
(1)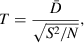 (2)
(2)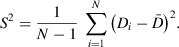 (3)
(3)Under the null hypothesis (H0), the EM and AM have equal predictive abilities, such that the average loss equals zero (i.e., 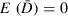 ). The structure of the CVPAT test statistic given in Equation (2) resembles the Diebold and Mariano (1995) test, which also considers the average loss differences divided by its variance. Although Diebold and Mariano (1995) introduced their test to support model selection in a time-series framework, CVPAT is designed to be used with cross-sectional data in which the losses are estimated by cross-validation. Analogous to the Diebold–Mariano test, CVPAT also represents a form of the paired t-test to investigate the average effect of treating each observation with a different model. Based on the use of cross-validated paired t-tests in the prior literature (Dietterich, 1998; Alpaydin, 2014), we evaluate the test statistic in Equation (2) with respect to a t-distribution with N – 1 degrees of freedom.4
). The structure of the CVPAT test statistic given in Equation (2) resembles the Diebold and Mariano (1995) test, which also considers the average loss differences divided by its variance. Although Diebold and Mariano (1995) introduced their test to support model selection in a time-series framework, CVPAT is designed to be used with cross-sectional data in which the losses are estimated by cross-validation. Analogous to the Diebold–Mariano test, CVPAT also represents a form of the paired t-test to investigate the average effect of treating each observation with a different model. Based on the use of cross-validated paired t-tests in the prior literature (Dietterich, 1998; Alpaydin, 2014), we evaluate the test statistic in Equation (2) with respect to a t-distribution with N – 1 degrees of freedom.4
SIMULATION STUDY
Design
To ensure researchers can reliably utilize CVPAT in their applications with real data, we assessed its performance in several Monte Carlo studies by systematically manipulating an expansive set of experimental conditions. The aim was to compare a population model (PM) to a misspecified model (MM) and calculate CVPAT's probability of selecting the PM (e.g., Ericsson, 1991).5
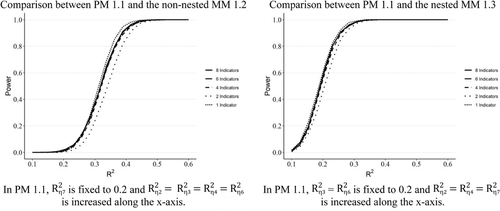
The simulation study used a relatively complex model setup (Figure 1) that mirrored the ACSI model's principal structure (Fornell et al., 1996) and reflects the typical degree of complexity seen in PLS studies in marketing, management, and other social science fields (e.g., Hair, Sarstedt, Ringle, & Mena, 2012b; Ringle et al., 2019). The data were generated based on PM 1.1 for the simulation study. This model was compared to a particularly challenging nonnested alternative for predictive purposes, MM 1.2, which used all latent variables as direct antecedents of the target construct η7. We also contrasted PM 1.1 to a parsimonious misspecified version, MM 1.3, to assess CVPAT's applicability in nested model comparisons that are widely encountered in empirical SEM research (Cagli, 1984; Pornprasertmanit, Wu, & Little, 2013).
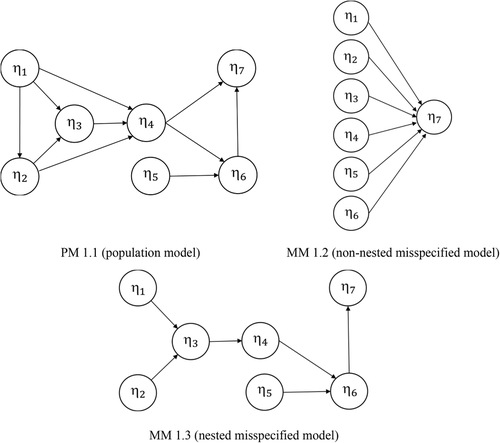
- Twenty conditions of equally spaced and increasing R2 values in the endogenous constructs ranging from .1 to .6, with the inner model coefficients changing accordingly.
- Five conditions of sample size (50, 100, 250, 500, and 1,000).
- Five conditions of varying numbers of indicators per construct (1, 2, 4, 6, and 8).
- Two conditions of loadings (.5 and .8).6
We generated normally distributed composite model data using the approach employed by Sarstedt, Hair, Ringle, Thiele, and Gudergan (2016), as well as by Hair, Hult, Ringle, Sarstedt, and Thiele (2017b).7 We also conducted additional analysis using nonnormal data, reported in the robustness checks section. We ran 3,000 replications of each of the factorial combinations, using the following settings: equal weights for initialization of the algorithm (Hair et al., 2017a), correlation weights for the outer model estimations in all the initial simulations (Wold, 1982; Chin, 1998), path weighting scheme for the inner model estimations (Lohmöller, 1989), and a stop criterion of 10−5 (Tenenhaus, Esposito Vinzi, Chatelin, & Lauro, 2005). All simulations were run using the R statistical software (R Core Team, 2019) on a parallel computing environment.
Results of the Power Analysis
We investigated CVPAT's ability to correctly reject the null hypothesis that the PM and the MM have equal predictive capabilities (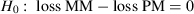 ) in favor of the alternative hypothesis that the PM has a higher predictive capability (i.e., a lower loss) than the MM (
) in favor of the alternative hypothesis that the PM has a higher predictive capability (i.e., a lower loss) than the MM (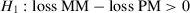 ). A specific factor combination's estimated power is calculated as
). A specific factor combination's estimated power is calculated as 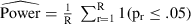 at the 5% significance level, where pr is the p-value of the rth Monte Carlo run, 1(·) is the indicator function, and R is the total number of Monte Carlo repetitions (Cameron & Trivedi, 2005). A power level of .8 signifies that CVPAT chose the PM in at least 80% of the simulation runs across the experimental conditions. Note, however, that a power level of .8 does not imply the CVPAT chose the incorrect model 20% of the time.
at the 5% significance level, where pr is the p-value of the rth Monte Carlo run, 1(·) is the indicator function, and R is the total number of Monte Carlo repetitions (Cameron & Trivedi, 2005). A power level of .8 signifies that CVPAT chose the PM in at least 80% of the simulation runs across the experimental conditions. Note, however, that a power level of .8 does not imply the CVPAT chose the incorrect model 20% of the time.
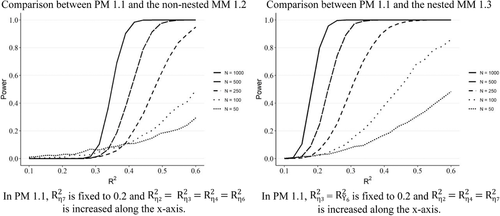
The graphs in Figure 2 show the power results with varying sample sizes when keeping the number of indicators fixed at four. The x-axis plots increasing levels of R² values for specific constructs. The discrepancy between the null and alternative hypothesis increases with an increase in R2 values, resulting in higher power levels for CVPAT.
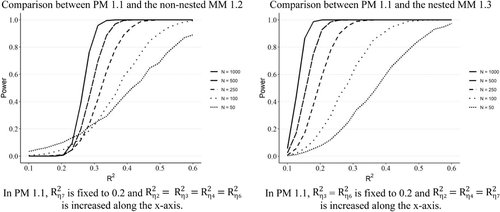
When comparing PM 1.1 with the nonnested MM 1.2, we found that CVPAT's power increased with sample size and R2 (Figure 2, left). With larger sample sizes (≥250), power levels surpassed the recommended threshold value of .8 at moderate R2 values of .35 (Cohen, 1988). With sample size 100, power levels passed .8 when R2 was higher than .45. In contrast, with smaller sample sizes (n = 50), power levels breached the .8 level only when R2 was higher than .55. For the nested model comparison between PM 1.1 and MM 1.3 (Figure 2, right), we found that power levels surpassed .8 for larger sample sizes (≥250) at relatively low R2 values of .25 and higher. A sample size of 100 required R2 to be greater than .35 for acceptable power, whereas small sample (n = 50) required relatively high R2 values of .5 and higher.
Next, we analyzed the effect of the number of indicators in the measurement model on the CVPAT power levels. Figure 3 shows that the number of indicators per construct did not have an appreciable effect on the power level. Although the results shown in Figure 3 are for a sample size of 250, these differences did not change noticeably with other sample sizes.
These results hold for acceptable item loadings of .8 for the construct's measurement. In contrast, low item loadings had a negative effect on the power. Figure 4 displays the power levels with four indicators per construct, each with a low loading of .5, which is less than the recommended threshold of .7. As can be seen in the figure, low loadings necessitated larger samples with much higher inner model R2 values to reach an acceptable power level. For example, sufficient power was achieved with a sample size of 250 only when the R2 was higher than .5 for the nonnested comparison, and .4 for the nested comparison. In particular, we found that sufficient power levels may not be achievable with sample sizes smaller than 100 and low item loadings. These results suggest that recommended levels of item loadings are required to achieve sufficient power levels when using CVPAT.
Overall, this analysis provides evidence that CVPAT is effective in correctly rejecting the null hypothesis with standard sample sizes and levels of measurement model loadings, and when the inner models show moderate to high levels of R2, as is generally seen in management research. Under these conditions, PLS researchers can confidently expect to achieve high power levels with CVPAT, underlining its practical utility for most research situations. With small sample sizes (e.g., 100), researchers can still expect to achieve satisfactory power levels, provided that R2 values are also high (.45 or higher). However, the use of CVPAT becomes impractical when sample sizes are smaller than 100 or when item loadings are low, because high R2 values may not be achievable under these circumstances, and thus sufficient power is not guaranteed.
Robustness Checks
We provide further evidence of CVPAT's practical utility by conducting several robustness checks that assessed its performance under a broader range of conditions. First, we assessed the CVPAT test statistic's reliance on the t-distribution. A test statistic that follows a t-distribution with N – 1 degrees of freedom is expected to incorrectly reject a true null hypothesis (i.e., Type I error) in 5% of cases given a .05 significance level. To determine whether our test statistic met this criterion, we conducted an additional model comparison study under the null hypothesis of equal predictive ability, assuming a t-distribution with N – 1 degrees of freedom and a .05 significance level. We repeated the analysis 3,000 times to calculate the percentage of runs in which the null hypothesis was falsely rejected. Table 1 shows the results of this simulation study. For an explanation of the models compared and the different factor levels considered in the simulation study, please see Online Supplement OS.3. The results show that the Type I error rates in general were slightly lower than 5%, which confirms that CVPAT is a well-sized, but mildly conservative inferential test.8
| Sample Sizes | |||||||
|---|---|---|---|---|---|---|---|
| Inner Model Coefficient | Number of Indicators | 50 | 100 | 250 | 500 | 1,000 | 10,000 |
| Low: .15 | 1 | .029 | .026 | .029 | .041 | .041 | .045 |
| 2 | .075 | .062 | .036 | .042 | .041 | .051 | |
| 4 | .066 | .048 | .030 | .037 | .040 | .059 | |
| 6 | .062 | .053 | .036 | .036 | .038 | .050 | |
| 8 | .073 | .051 | .027 | .034 | .042 | .049 | |
| Medium: .3 | 1 | .043 | .046 | .047 | .042 | .045 | .042 |
| 2 | .056 | .046 | .041 | .049 | .038 | .043 | |
| 4 | .044 | .042 | .037 | .039 | .039 | .045 | |
| 6 | .045 | .039 | .038 | .045 | .037 | .043 | |
| 8 | .038 | .048 | .036 | .038 | .037 | .051 | |
| High: .5 | 1 | .047 | .042 | .040 | .034 | .036 | .040 |
| 2 | .049 | .047 | .033 | .043 | .042 | .039 | |
| 4 | .041 | .040 | .038 | .040 | .028 | .039 | |
| 6 | .040 | .043 | .036 | .037 | .039 | .040 | |
| 8 | .042 | .038 | .032 | .037 | .040 | .034 | |
Second, we assessed the effect of nonnormally distributed data on CVPAT's power level by re-running the model setup shown in Figure 1. We used exponential distribution with a scale parameter of one, kurtosis six, and skewness two (for simulations with nonnormal data in PLS, also see Ringle, Sarstedt, & Schlittgen, 2014). As shown in Figure OS.2 (Online Supplement OS.4), nonnormality adversely affected CVPAT power levels. In general, compared to normal data (c.f. Figure 2), CVPAT required somewhat higher levels of R2 to achieve similar power for each sample size. For example, a sample size of 250 required an R2 value of at least .45 for the nonnested comparison and .3 for the nested comparison. Moreover, a small sample size of 100 required an R2 of at least .55 for nonnested comparison, and .45 for nested comparison. With smaller sample sizes (n = 50), sufficient power levels may be very difficult to achieve in practice, in which case the use of CVPAT is not recommended.
Third, we investigated CVPAT's performance for measurement models with formative indicators (Sarstedt et al., 2016; Bollen & Diamantopoulos, 2017). This analysis compared PM 1.1 with the nested MM 1.3. However, in both models, η1 was now specified as a formative construct and we used regression weights to estimate their outer weights (Rigdon, 2012; Becker et al., 2013). The power results with the formative measurement model generally mirrored those of the reflective measurement model (Figure OS.3 in Online Supplement OS.4). In particular, the sample size and R² values continued to be the primary drivers of CVPAT power levels.
Fourth, we investigated CVPAT's performance in the presence of mediation effects that are widely assessed in PLS (Nitzl, Roldán, & Cepeda Carrión, 2016; Hair et al., 2017a). Figure OS.4 in Online Supplement OS.5 shows the simple model setup with three reflective constructs similar to the study by Henseler and Sarstedt (2013). Model 2.1 has two relationships, that is, between η1 and η2, and between η2 and η3. Thus, η2 (fully) mediates the relationship between η1 and η3. In contrast, Model 2.2 has no relationship between η2 and η3, but a relationship between η1 and η3. To mitigate the possibility of bias against a specific type of model structure, each of the two models acted as the PM in turn, whereas the other acted as the MM. This resulted in two model comparison cases. For each case, we assessed CVPAT's performance in selecting the PM. The results show that power levels easily surpassed .8 in both cases for sample sizes of 100 or more and when the R² was .25 or higher (Figure OS.5 in Online Supplement OS.5). Similar to our main analysis (Figure 4), we found that low item loadings (.5) had a negative effect (Figure OS.6 in Online Supplement OS.5), but the number of indicators did not have any noticeable effect on power (Figure OS.7 in Online Supplement OS.5). We also found that the effect of nonnormality was less pronounced in the simple model setup (Figure OS.8 in Online Supplement OS.5) than in the complex model setup (Figure OS.2 in Online Supplement OS.4). This analysis confirms CVPAT's practical utility when dealing with both mediation and nonmediation model comparisons across a wide range of factor levels.
Fifth, we considered that researchers can implicitly assume that the model with the highest number of predictors is the best predictive model due to its high R2 value, although overspecified models often offer weaker predictive outcomes (Shmueli & Koppius, 2011). We therefore investigated whether CVPAT has a systematic tendency to select a more complex model (i.e., overfitting) by conducting an additional simulation study that compared the PM with more complex, systematically overspecified model alternatives; that is, the MMs included more paths than the PM (Figure OS.9 in Online Supplement OS.6). As expected, additional predictors in the overspecified models improved their in-sample explanatory power (R2) (Figure OS.10 in Online Supplement OS.6). At the same time, however, as the increased loss indicates, their out-of-sample predictive capabilities decreased, suggesting overfitting. Although the PM had the lowest explanatory power (as expressed by the lowest R² value), it had the highest out-of-sample predictive power. This finding is not surprising, because the model with the highest in-sample explanatory power might not be the best model for out-of-sample prediction (Sharma et al., 2019a; Sharma et al., 2019b). CVPAT's average loss function showed the lowest value for the PM, whereas the average loss increased with the level of model overspecification. Overall, these results substantiate that CVPAT avoids selecting falsely overspecified models.
Finally, we analyzed the probability of incorrectly choosing an overspecified model as a better predictive alternative compared to a proposed PM. In order to do so, we used the simulations in the previous paragraph, where a parsimonious PM was tested against a systematically overspecified model alternative. We found that the use of CVPAT reduced the probability of choosing an incorrect model substantially in comparison to using a rule of thumb for selecting the model with the lowest loss. For instance, when considering the two-indicator case and one overspecification in the MM, approximately 85% of the results had the correct signs in the loss differences (Figure OS.11, left, in Online Supplement OS.6). In other words, by simply relying on a rule of thumb, researchers can expect about 15% of their decisions to be false. However, by relying on CVPAT, researchers can expect substantially better outcomes. In fact, the probability of selecting a false overspecified model is close to zero with CVPAT regardless of the degree of overspecification (Figure OS.11, right, in Online Supplement OS.6).
APPLICATION OF CVPAT
Procedure
We propose a stepwise prediction-oriented model selection procedure to enable researchers and practitioners to systematically apply CVPAT in their PLS analyses (Figure 5). Step 1 involves the selection of two theoretically motivated models to be compared for their out-of-sample predictive abilities. Because PLS analyses focus on providing causal explanations (Jöreskog & Wold, 1982; Chin, 1995), the models selected for comparison must be based on valid theoretical reasoning and might not be purely empirically motivated (Sharma et al., 2019a). In accordance with the null hypothesis testing practice, the model that represents the current state of theoretical knowledge typically serves as the EM, whereas the model that the researcher is proposing serves as the AM. Because the EM represents the status quo, it serves as the null hypothesis and is only rejected if there is strong statistical evidence against it (Larsen & Marx, 2018). For example, in customer satisfaction research, Olsen and Johnson (2003) propose an alternative “satisfaction-first” model that is compared to the widely accepted “equity-first” formulation of customer loyalty. The specific goal of the CVPAT analysis is to test whether the AM offers a statistically significant improvement over the EM in its out-of-sample predictive power.
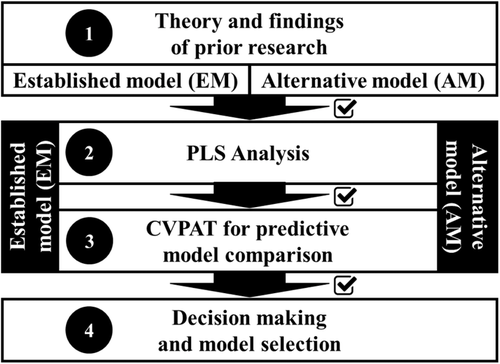
In Step 2, the researcher must ensure the suitability of the empirical context for a fair model comparison and conduct the PLS analysis for both the EM and the AM to assess whether the models meet the established requirements in terms of data and measurement quality (Hair et al., 2017a). First, the researcher must ensure that the data collection procedure follows the established guidelines for sample representativeness and minimum sample size requirements for PLS (Hair et al., 2017a). Second, a specific model comparison aspect requires the empirical context to be unbiased, that is, the observed difference in predictive abilities should be attributable to models themselves, rather than to the specific sample chosen for comparison. An objective and fair model comparison process requires data that do not unfairly favor one theory over another (Cooper & Richardson, 1986).9 In addition, it is important that the constructs use the same measurement model in the EM and AM (i.e., the same indicators) and the same mode of model estimation (i.e., Mode A or B) for a valid comparison. Other settings also have to be identical in the EM and AM estimations (e.g., missing data treatment, PLS algorithm settings). Finally, both the EM and the AM have to meet the established measurement model evaluation criteria (Chin, 1998; Hair, Risher, Sarstedt, & Ringle, 2019a).
Step 3 compares the EM and the AM for their out-of-sample predictive power by using CVPAT. The goal is to identify the model with higher out-of-sample predictive accuracy. The two key CVPAT algorithm settings are the number of cross-validation folds and bootstrap samples. Prior literature suggests the use of five- or 10-folds (e.g., Hastie et al., 2009) and 5,000 or more bootstrap samples (e.g., Hair et al., 2017a).
Finally, in Step 4 the researcher selects a model based on the CVPAT outcome. If the AM has a higher loss than the EM, the researcher retains the EM as the predictive model of choice. In contrast, a statistically significant (i.e., p < .05) positive loss difference (i.e., loss EM – loss AM > 0) is interpreted as evidence that the null hypothesis is incompatible with the observed data (Greenland et al., 2016). It is important to note that a small p-value only suggests relative support for the AM based on the comparison with the EM, and does not convey any information about the size of the loss difference or its practical significance (Wasserstein & Lazar, 2016). Researchers should further consult evidence provided by the 95% confidence interval along with the p-value to make the decision (Ferguson & Speier-Pero, 2017). Table 2 summarizes the decision-making based on the CVPAT results in Step 4.
| EM is Favored A Priori Over AM | |
|---|---|
| One-Sided Significance test | Conclusion |
 |
Cannot reject H0: retain EM |
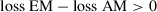 |
Reject H0: choose AM |
- H0:
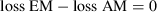 and H1:
and H1: 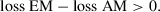
- Abbreviations: EM, established model; AM, alternative model; loss, average prediction error.
Empirical Illustration
We illustrate the application of CVPAT on empirical data to showcase its utility and provide additional validation. We draw on the ACSI, which is one of the most widely used models in business research and practice for analyzing the impact of customer satisfaction on repurchase intentions or customer loyalty (Fornell et al., 1996; Anderson & Fornell, 2000).10 The ACSI conceptualizes customer satisfaction as a cumulative construct and asks customers to rate their overall experience with the provider to date. This contrasts with transaction-specific satisfaction models that evaluate satisfaction based on customers’ experience related to a specific product or service transaction (Olsen & Johnson, 2003). The main benefit of cumulative evaluations is they are better predictors of customer behavior. Figure 6 (left) shows the ACSI model, which is widely supported by research (e.g., Fornell et al., 1996; Hult, Sharma, Morgeson, & Zhang, 2019), and thus serves as the EM in Step 1 of the procedure. The model consists of five reflectively measured constructs: customer satisfaction (ACSI), customer expectations (CUEX), customer loyalty (CUSL), perceived quality (PERQ), and perceived value (PERV).11
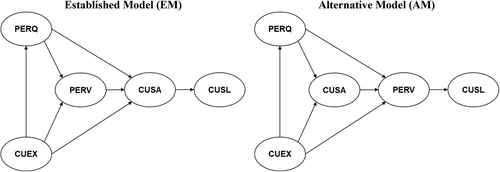
We focused on the causal link between PERV, CUSA, and CUSL to identify a theoretically motivated AM for the purpose of our illustration. The majority of customer research supports the “value-first” conceptualization of the EM where PERV serves as the immediate antecedent of customer satisfaction (CUSA) (Hult et al., 2019). In contrast, research in customer value equity literature suggests an alternative “satisfaction-first” conceptualization, where PERV mediates the effect of CUSA on CUSL, particularly when cumulative satisfaction is being considered for customers who have had no reason to complain (Johnson, Gustafsson, Andreassen, Lervik, & Cha, 2001). For example, Olsen and Johnson (2003) argue that customers’ cumulative satisfaction determines their value equity judgments when they are making repurchase decisions.12 Cumulative satisfaction is therefore seen as the direct cause of customers’ attitude formation regarding the value associated with a product or service provider. In other words, satisfied customers with no reason to complain in the long run are likely to perceive the provider's service as “good value for money,” which affects their loyalty positively (Vogel, Evanschitzky, & Ramaseshan, 2008). Related research by Chang and Wildt (1994) also supports the direct effect of PERV on repurchase intentions, which is an item of CUSL. Based on this line of reasoning, we propose an AM (i.e., the “satisfaction-first” research model) as depicted in Figure 6 (right). The two models (EM and AM) form the starting point of our illustration of the stepwise predictive model comparison procedure using CVPAT. The main question of interest is: which of the two theoretical models (i.e., EM and AM) exhibits higher out-of-sample predictive ability?
In Step 2, to ensure a fair comparison among the models, we followed Olsen and Johnson's (2003) recommendations and focused only on the customers of the utilities industry who did not complain.13 Previous research has validated the applicability of both the EM (e.g., Schlittgen, Ringle, Sarstedt, & Becker, 2016) and the AM (e.g., Olsen & Johnson, 2003) for such customers. Our final sample consisted of 2,854 unique survey responses.14 For the PLS model creation, estimation, and validation, we utilized the SmartPLS 3 software (Ringle, Wende, & Becker, 2015). Online Supplements OS.7 and OS.8 present the PLS results of the EM and AM. The outcomes of both models meet the established evaluation criteria of PLS for the measurement models and the structural model (e.g., Chin, 1998; Hair et al., 2017a).
Next, we ran a CVPAT-based model comparison (Step 3) using our own code for R statistical software (R Core Team, 2019).15 The goal was to determine whether the AM offers significantly higher predictive power than the EM. We therefore tested the EM against the AM using a one-sided hypothesis test.16 The null hypothesis proposes equal out-of-sample predictive abilities (i.e., H0: Loss of EM = Loss of AM), whereas the alternative hypothesis proposes that the AM has lower average loss than the EM (i.e., H1: Loss of EM > Loss of AM).
We found that the EM exhibited lower loss (.682) than the AM (.690), which supported retaining the EM as the best predictive model (Table 3). The high p-value of 1 indicated that we cannot reject the null hypothesis of the two models having equal predictive ability given the alternative hypothesis. The same inference was supported by the 95% CI.
- Note: A negative average loss value difference between the EM and AM indicates that the EM has a smaller average loss and is therefore preferable. If the average loss value difference is positive, the AM has superior predictive power.
- a The null hypothesis is equal predictive ability and the alternative hypothesis is that the AM (column 3) has better predictive ability than the EM (column 2); the p-value is based on 10,000 bootstrap samples.
- b CI = 95% confidence interval of the one-sided test.
- Abbreviations: EM, established model; AM, alternative model.
Step 4 focuses on the final decision-making and model selection. Based on the empirical evidence, we chose to retain the EM, which offers higher predictive accuracy than the AM. Overall, the results support the PERV’s theoretically established role as a predecessor of CUSA as conceptualized in the original ACSI model for improving the predictive accuracy of the ACSI model.17
DISCUSSION
Findings
Management and business disciplines are inherently forward-looking where anticipation is a crucial element for making successful policy decisions. To remain ahead of the competition, management experts and practitioners invest heavily not only in identifying the current trends and perceptions, but also in preparing for unforeseen changes in the dynamic social, technological, and economic environment. In this vein, the prospective outlook of predictive modeling, in which a model is constructed to predict unseen or new data, can provide a valuable lens for theoretical validation that complements the retrospective (or postdictive) nature of causal-explanatory modeling that dominates the field (Gauch & Zobel, 1988; Shmueli, 2010).
From an academic standpoint, predictive modeling is valuable for theory construction and enhancement via comparison, relevance assessment, improvement in measures and construct operationalizations, and benchmarking the predictability of a given phenomenon (Shmueli et al., 2016; Hofman et al., 2017). From a practitioner's perspective, the focus is not typically on validating or testing theories, but rather on generalizable approaches or policies with immediate commercial utility or predictive power (Ruddock, 2017).
Predictive modeling has the potential to engage stakeholders on both sides of the theoretical spectrum. A sharper focus on a model's predictive abilities can help to connect the subjective and objective realities by helping assess the distance between theory and practice, and narrowing the range of possibilities to ensure successful policy making (Shmueli & Koppius, 2011; Silver, 2012). PLS emphasizes prediction in estimating statistical models with a structure designed to simultaneously provide theoretical explanation (Wold, 1982; Lohmöller, 1989). To fulfill its initial promise as a predictive technique, PLS researchers need to have proper tools to reliably conduct and compare the out-of-sample predictive abilities of their models—as recent research calls have indicated (e.g., Richter, Cepeda Carrión, Roldán, & Ringle, 2016). To this end, we introduce the CVPAT—a procedure that permits researchers to develop and examine theoretical models through a predictive lens rather than with purely explanation-oriented model evaluation metrics. More specifically, by relying on cross-validation and out-of-sample prediction errors and allowing for the null hypothesis testing of two competing models (i.e., the EM against an AM), CVPAT distinguishes itself from current PLS-based explanatory fit criteria that support the postdictive approach to model building (e.g., SRMR and exact fit; Henseler et al., 2014).
Our simulations confirm CVPAT's capability to reliably assess an established model's predictive performance compared to that of an alternative model. Furthermore, our simulations point to CVPAT's potential to help detect the best inner model for prediction purposes. We find that CVPAT performs in accordance with the expectations of a null hypothesis-based test (Cameron & Trivedi, 2005). Specifically, our simulation results reveal that CVPAT has very high power with sample sizes of 250 and more, and when the measurement model loadings are .8. With lower sample sizes, researchers can still expect to achieve satisfactory CVPAT power levels when R2 values are .4 or higher. However, CVPAT power levels are generally below the recommended threshold of .8 when sample sizes are 100 or smaller. The number of indicators per construct and model complexity do not have a significant impact on the power levels. Moreover, CVPAT is well sized but slightly conservative, and it does not show a tendency to systematically choose the model with the highest number of predictors (i.e., highest R2). Due to its favorable characteristics and performance across a wide range of model and data constellations, CVPAT can be a valuable tool to support both researchers and practitioners in their prediction-oriented model assessments.
Guidelines to avoid pitfalls in the application of CVPAT
Although the assessment of a model's predictive power is well documented in prior PLS research (Shmueli et al., 2016; Danks & Ray, 2018), predictive model comparisons have remained unaddressed, with few available guidelines. Hence, we issue several clarifying remarks below to help researchers avoid certain pitfalls when applying CVPAT:
Role of theory is paramount
A sound theoretical basis for the proposed and the alternative models is mandatory in order to ensure that the analysis focuses on a limited number of theoretically plausible model alternatives (Sharma et al., 2019a). The proposed stepwise procedure should not be used in data-driven searches for a model that offers best predictive fit but lacks theoretical foundation. Other purely predictive methods, such as neural networks, support such a goal better than PLS—the latter technique seeks to balance explanation and prediction. Comparing a limited number of theoretically plausible models also safeguards against difficulties related to multiple comparisons. Although approaches for maintaining the familywise error rate of statistical tests (e.g., the Bonferroni correction) can be applied to CVPAT, there is no clear consensus on when to apply them, because their use often causes substantial increase in Type II error rates (Cabin & Mitchell, 2000).
In-sample and out-of-sample assessments might differ
In-sample model assessment criteria might not agree with CVPAT's out-of-sample prediction assessments, because they serve different purposes (Shmueli & Koppius, 2011). For instance, the best predictive model may not necessarily offer the highest in-sample explanatory power (i.e., highest R²) or the greatest number of statistically significant paths (Lo, Chernoff, Zheng, & Lo, 2015). It is also important to note that CVPAT does not represent an all-encompassing assessment of PLS results. Instead, researchers should carefully define the specific goal of their research and apply the metrics that support it. For example, when the focus is on explaining trends specific to the sample-at-hand, researchers should rely on the in-sample explanatory criteria, such as R2, but with the caveat that the inferences drawn will be tailored to the specific context being studied, with little or no justification for generalizability to other datasets (Ward, Greenhill, & Bakke, 2010). However, CVPAT should be preferred when the main analytic goal is prediction and theoretical generalization beyond the sample-at-hand, because cross-validation provides an assessment of the generalization error. Models selected for their out-of-sample predictive ability are more likely to apply well to other, similar contexts (Yarkoni & Westfall, 2017).
Statistically significant loss differences do not automatically imply predictive relevance
In large samples, even small loss differences can become statistically significant, whereas large loss differences may fail to reach statistical significance in small samples (Lin, Lucas, & Shmueli, 2013). This holds for null hypothesis testing in general, as well as for CVPAT, because the differences in the predictive power of models—while significant—can sometimes be marginal. Researchers can make more informed decisions regarding the relevance of loss differences by constructing confidence intervals that provide more information in the form of the range of actual values and the precision of the estimates (Gardner & Altman, 1986).
CONTRIBUTION AND FUTURE RESEARCH
The PLS method plays an important role in management studies and broader social sciences (e.g., Mateos-Aparicio, 2011) to develop robust theories that offer both explanation and prediction in parallel (Evermann & Tate, 2016; Shmueli et al., 2016). Researchers place great emphasis on in-sample explanatory power and model specifications, but ignore the out-of-sample predictive performance of PLS models. We address this imbalance and gap in research practice by introducing CVPAT as a means to conduct a pairwise comparison of models for their out-of-sample predictive abilities. Our complex simulation study shows that CVPAT is a reliable and practical tool for researchers. Applying CVPAT allows researchers and practitioners to compare EMs with theoretically motivated AMs to provide stronger evidence of theoretical progress. More specifically, by offering the means to compare competing PLS path models in terms of their out-of-sample predictive power, CVPAT contributes to management research and practice in the following respects:
Theory Validation and Development
Documenting the predictive superiority of one model over another is a crucial aspect of theory validation that offers direct evidence regarding whether the current theory development effort has been successful (Shmueli, 2010). When comparing the predictive abilities of two competing theories in such a manner, the focus should be less on assessing the statistical significance of the individual paths (or variables) in the models, and more on holistically assessing whether a model offers significantly better predictions than its rival model. This is because a statistically significant variable in a model does not automatically imply stronger prediction. In fact, a variable with strong predictive power can sometimes fail to be statistically significant (Shmueli & Koppius, 2011). Thus, relying on statistical significance at the individual path or variable level can result in the researcher overlooking highly predictive variables (Lo et al., 2015). CVPAT offers a means of statistically comparing predictive power at the model level, thereby aiding theory development via (relative) predictive power assessments and identification of variables with high predictive power.
Reduced Uncertainty in Model Selection
Researchers typically rely on out-of-sample error metrics, such as RMSE or MAE, to judge their models’ predictive accuracy. These metrics, however, do not have well-defined thresholds, which renders any relative judgments about the quality of model predictions arbitrary (Roy, Das, Ambure, & Aher, 2016). In addition, because out-of-sample prediction is a data-driven activity (Shmueli & Koppius, 2011), ruling out chance as an alternative explanation is a valuable and necessary step in theory confirmation (Lempert, 2009). Using CVPAT enables researchers to statistically compare the predictive strengths of models to judge whether model choice is reliable and not affected by chance or sampling error.
The Ability to Quantify Loss (Gain) in Predictive Accuracy
CVPAT enables researchers to quantify the loss in predictive accuracy associated with the models being compared, and to assess how far their predictions are from the observed value. Recall that loss represents the penalty for inaccurate predictions in that a model with higher associated loss has inferior predictive accuracy compared to a model associated with lower loss. Quantifying predictive accuracy via the loss functions has been the bread and butter of machine learning researchers. Research using the PLS method has lacked a mathematically rigorous and objective measure to indicate whether theoretical modeling has been successful in capturing information that will also apply beyond the sample-at-hand. For example, it is widely known that adding more variables (or paths) to the model will increase the model's ability to fit the observed data (e.g., R2). The use of CVPAT can provide complementary information regarding whether the inclusion of the variable(s) has resulted in improved out-of-sample predictive accuracy, and if so, by how much.
Improved Confidence in Decision-Making
Prediction is pivotal for making decisions under conditions of uncertainty, and in creating opportunities to compete for fresh business strategies (Agrawal, Gans, & Goldfarb, 2018). Decision makers regularly face binary choices while designing and reviewing crucial policies that require a decision on whether to take a specific course of action or not. They often wonder whether their policies will work well in other situations (Snow & Phillips, 2007). CVPAT makes such decisions less error-prone by reducing generalization error so that the policy decisions will be more likely to work in other settings (Markatou et al., 2005).
A Useful Tool to Avoid Overfitting
Overfitting occurs when a model confuses spurious patterns (sample-specific noise) in the data as signal. Sole reliance on the in-sample fit measures (e.g., R2) means that there is always an incentive to overfit the models by introducing more parameters than are needed, because R2 increases with model complexity by simultaneously tapping both noise and the signal (Sharma et al., 2019a). CVPAT helps guard against overfitting because the cross-validation procedure assists in recovering the signal in the data minus the noise (Yarkoni & Westfall, 2017). As researchers build their models by progressively adding more parameters, explanatory power will continue to rise, whereas predictive accuracy will taper off and decrease after peaking at the so-called “Ockham's hill” (Gauch, 1993). This point of divergence between the in-sample explanatory power and out-of-sample predictive accuracy reflects the regime of overfitting.
Future Research
CVPAT is certainly not a panacea for all PLS modeling efforts. Varoquaux (2018, p. 5) notes, however, that cross-validation (as implemented in CVPAT) “is the best tool available, because it is the only non-parametric method to test for model generalization.” In order to further improve the method's usefulness, future research should address our study's limitations. First, although CVPAT reduces uncertainty regarding predictive model selection, it does not focus on the accurate prediction for single cases. Future research can investigate predictive errors on the level of single observations when applying CVPAT. Second, CVPAT permits assessing whether an AM has a significantly higher predictive accuracy than the EM, when considering all constructs in the model simultaneously. However, the method can be readily extended to assess losses at the level of a specific construct to complement the single target construct-oriented model selection based on the BIC and GM criteria proposed by Sharma et al. (2019b). Such an assessment would enable researchers to identify constructs that have a diminishing effect on the model's predictive power, which would be particularly valuable as the statistical significance of path coefficients offers no guidance in this respect (Ward et al., 2010). Third, CVPAT might have the potential to identify misspecifications of measurement models. For example, an exogenous indicator could have a high cross loading with another exogenous construct. CVPAT could be used to show which construct the indicator should be assigned to when the main objective is the prediction of the endogenous latent variables. However, improving indicator allocation based on CVPAT must always be guided by theoretical reasoning. Future research should address this worthwhile CVPAT extension. Fourth, future research should fully address the statistical significance versus relevance question when comparing models for their predictive accuracy. For instance, predetermined levels of minimum loss differences could be established to guide researchers in deciding whether a small, but significant, loss difference is relevant to select an AM over a theoretically established model. Fifth, as with all simulation studies, the results depend on the manipulated factors and their levels. In line with prior publications on cross-validation in machine learning (e.g., Kim, Park, & Williams, 2019), we used 10-folds for the CVPAT. Future research could address the question whether 10-folds is an adequate parameter when running the CVPAT in detail. Also, it would be beneficial to investigate whether the complex models’ relatively low power is due to the mixture of low and high inner coefficients, or whether it is the consequence of model complexity. Studying the effect of other data distributions can offer further insight into CVPAT's performance in settings commonly encountered in management research (e.g., model complexity in relation to sample size and/or R² values required to ensure sufficient power). Similarly, future CVPAT simulation studies should analyze a broader range of AMs and their different forms of model misspecification. Sixth, our empirical illustration is limited to a prominent example from the literature. Future research should assess CVPAT on a broader range of empirical applications with different kinds of theoretically substantiated model alternatives. These results would be important to support the adequacy and relevance of CVPAT in practical applications. Also, the outcomes of these applications would allow comparison of the EM with potential alternatives and, based on the results, provide additional clarification for the model choice in subsequent applications. For example, the analysis of the UTAUT model in information systems research (e.g., Shiau & Chau, 2016) can be a particularly fruitful area for future CVPAT applications. Finally, we have assessed CVPAT's abilities for PLS analyses. However, the method is also amenable to alternative composite-based structural equation modeling methods such as generalized structured component analysis (GSCA) (Hwang & Takane, 2014; Hwang, Sarstedt, Cheah, & Ringle, 2020). Future research should expand the use of CVPAT to such related methods.
ACKNOWLEDGMENTS
The authors would like to thank Edward E. Rigdon, Georgia State University, and John D'Arcy and Kathryn Berkow, University of Delaware, for their helpful comments on earlier versions of the manuscript. This research uses the statistical software SmartPLS (http://www.smartpls.com). Ringle acknowledges a financial interest in SmartPLS.
Biographies
Benjamin Liengaard is a PhD fellow at the Department of Economics and Business Economics, Aarhus University. His main research interest is in partial least squares path modeling and quantitative analysis in the field of business analytics.
Pratyush Nidhi Sharma is an assistant professor in the Alfred Lerner College of Business & Economics, University of Delaware. Beginning August 2020, Dr. Sharma will be on the faculty of Information Systems, Statistics and Management Science in the University of Alabama's Culverhouse College of Business. He can be reached at [email protected]. He received his PhD from University of Pittsburgh in 2013. His research interests include online collaboration communities and networks, open source software development, and research methods used in information systems, particularly partial least squares path modeling. In addition, he is also interested in issues surrounding technology use and adoption and human computer interaction. His research has been published in highly acclaimed journals such as the Journal of the Association for Information Systems, Journal of Retailing, Journal of Information Systems, Journal of Business Research, Journal of International Marketing, and International Journal of Accounting Information Systems. In addition, he has published several book chapters, and presented his research at premier conferences such as the International Conference on Information Systems (ICIS), Americas Conference on Information Systems (AMCIS), INFORMS, and PLS.
G. Tomas M. Hult is Professor and Byington Endowed Chair in the Broad College of Business at Michigan State University and a researcher at the American Customer Satisfaction Index (ACSI). He is a member of the Expert Networks of the World Economic Forum and United Nations/UNCTAD's World Investment Forum. He is a fellow of the Academy of International Business and the 2016 Academy of Marketing Science/CUTCO-Vector Distinguished Marketing Educator. He is also a visiting professor in the international business groups at Leeds University, United Kingdom, and Uppsala University, Sweden. His most recent book is The Reign of the Customer: Customer-Centric Approaches to Improving Customer Satisfaction (released by Palgrave Macmillan in 2020).
Morten Berg Jensen is an associate professor of business statistics at the Department of Economics and Business, Aarhus University. He holds a doctoral degree from Aarhus University. He specializes in research involving quantitative analysis of problems related to business and market research, and health economics.
Marko Sarstedt is a chaired professor of marketing at the Otto-von-Guericke-University Magdeburg (Germany) and an adjunct professor at Monash University Malaysia. His main research interest is the advancement of research methods to further the understanding of consumer behavior. His research has been published in Nature Human Behavior, Journal of Marketing Research, Journal of the Academy of Marketing Science, Multivariate Behavioral Research, Organizational Research Methods, MIS Quarterly, and Psychometrika, among others. According to the 2019 F.A.Z. ranking, he is among the three most influential researchers in Germany, Austria, and Switzerland. Marko has been named member at Clarivate Analytics’ Highly Cited Researchers List, which includes the “world's most impactful scientific researchers.”
Joseph F. Hair, Jr. holds Cleverdon Chair of Business in the Mitchell College of Business, the University of South Alabama. In 2018 and 2019, he was recognized by Clarivate Analytics for being in the top 1% globally of all business and economics professors based on his citations and scholarly accomplishments. He has authored over 80 book editions, including Multivariate Data Analysis, Cengage Learning, U.K., 8th edition 2019; Essentials of Business Research Methods, Routledge, 4th edition 2020; Essentials of Marketing Research, McGraw-Hill, 5th edition 2020; and A Primer on Partial Least Squares Structural Equation Modeling, Sage, 2nd edition 2017. He also has published numerous articles in scholarly journals such as the Journal of Marketing Research, Journal of Academy of Marketing Science, Organizational Research Methods, Journal of Advertising Research, Journal of Business Research, Journal of Long Range Planning, Industrial Marketing Management, Journal of Retailing, and others. He is writing a new book on Marketing Analytics, forthcoming in 2020 (McGraw-Hill).
Christian M. Ringle is a chaired professor of management at the Hamburg University of Technology (TUHH), Germany, and an adjunct professor of the University of Waikato, New Zealand. His research addresses human resource management, organization, marketing, strategic management, and quantitative methods for business and market research. His articles have been published in journals such as International Journal of Human Resource Management, International Journal of Research in Marketing, Information Systems Research, Journal of the Academy of Marketing Science, Long Range Planning, Organizational Research Methods, and MIS Quarterly. Christian's works have been awarded with several citation and best paper awards. He has been included in the Clarivate Analytics’ Highly Cited Researchers list. More information: https://www.tuhh.de/hrmo/team/prof-dr-c-m-ringle.html
REFERENCES
- 1 Online Supplement OS.1 presents a detailed mathematical description of the PLS methodology.
- 2 Gregor (2006) distinguishes between scientific theories that are geared more toward explanation (e.g., evolutionary theory), prediction (e.g., the standard model of particle physics), or both explanation and prediction (e.g., Shannon's [1948] information theory). Management and social science theories typically seek to explain the underlying causal mechanisms, as well as to provide verifiable and generalizable predictions, to enhance the scope and practical utility of research.
- 3 The training set is the subset of data on which the predictive model is built. The model is then applied and tested on the holdout set to assess its generalization error (Shmueli & Koppius, 2011).
- 4 We provide evidence regarding the validity of our use of the t-distribution in the robustness checks section. Alternatively, bootstrapping can be used to derive the p-values and confidence intervals.
- 5 In practical CVPAT applications, researchers compare the EM against an AM, both of which have been established on theoretical grounds. However, we use a different more suitable terminology for the simulation study, and refer to the models being compared as PM and MM.
- 6 In the additional one-indicator composite simulation case, the loadings should be set to one in order to comply with composite data generation.
- 7 We also generated factor model data using the method recommended by Reinartz, Haenlein, and Henseler (2009) and Sarstedt, Hair, Ringle, Thiele, and Gudergan (2016). This alternative data generation approach leads to very similar results, findings, and conclusions. The only notable difference is related to the number of indicators per measurement model. In contrast to composites, a lower number of indicators does have a negative effect on the power levels when considering common factors.
- 8 The probability of making a Type I error is sometimes called the size of the test (Cameron & Trivedi, 2005, p. 246). Accordingly, by “well-sized” we mean that the true size of the test corresponds well to the nominal size of the test. That is, when the researcher uses a test on a significance level of 5% (nominal size) and the null hypothesis is true, s/he will also falsely reject the null hypothesis in approximately 5% of the cases.
- 9 To avoid this issue, the context chosen for comparison must respect the application domain and the specific boundary conditions of the models involved. For example, Mathieson (1991) compared the technology acceptance model (TAM) and the theory of planned behavior (TPB) for their ability to explain individuals’ intentions to use information technologies. Although TAM was designed to maximize applicability across different technologies and user populations, TPB is context specific and requires specific outcomes and referent groups. Mathieson (1991) provides a theoretical rationale as to why the empirical context chosen for the study is appropriate for both TAM and TPB to ensure a fair comparison.
- 10 The ACSI has become the favored performance indicator for companies and government agencies, as well as entire industries and sectors (Fornell, Morgeson, & Hult, 2016; Hult, Morgeson, Morgan, Mithas, & Fornell, 2017).
- 11 In accordance with prior research, we utilize a modified version of the original ACSI model without the customer complaint construct for which the measurement relies on a single dummy-coded item; in addition, CUSL only uses a single indicator, and indicator cuex3 has been dropped because of its low outer loading (e.g., Rigdon, Ringle, Sarstedt, & Gudergan, 2011; Ringle, Sarstedt, & Schlittgen, 2014).
- 12 Value equity is defined as the perceived ratio of what is received (e.g., the quality of a product or service) to what is sacrificed (e.g., price paid; Vogel, Evanschitzky, & Ramaseshan, 2008). PERV, however, is largely similar to value equity and also captures customers’ perceptions regarding the quality of products and services in relation to the price (Olsen & Johnson, 2003).
- 13 We would like to thank Claes Fornell and the ICPSR for making the ACSI data available.
- 14 Note: The findings of this example do not substantially change when using the full sample (i.e., including customers who did and did not complain).
- 15 The CVPAT code for the statistical software R and technical instructions for its application are available for download at the following webpage: https://github.com/ECONshare/CVPAT/.
- 16 It is also possible to carry out a two-sided test. In this case, the EM and the AM are considered equally suitable model alternatives a priori. A significant CVPAT result could provide evidence in favor of the one or the other model; if not, we cannot reject their having equal predictive accuracy.
- 17 In contrast to Olsen and Johnson (2003) results that favor CUSA as a predecessor, the CVPAT results support the original conceptualization of the ACSI model for the utilities industry. One possible explanation for this discrepancy is that Olsen and Johnson (2003) compare the models for their fit and R2, which are in-sample tests for model adequacy but are not geared for assessing their true out-of-sample predictive abilities (Shmueli & Koppius, 2011).




