Application of single-step genomic best linear unbiased prediction with a multiple-lactation random regression test-day model for Japanese Holsteins
Abstract
This study aimed to evaluate a validation reliability of single-step genomic best linear unbiased prediction (ssGBLUP) with a multiple-lactation random regression test-day model and investigate an effect of adding genotyped cows on the reliability. Two data sets for test-day records from the first three lactations were used: full data from February 1975 to December 2015 (60 850 534 records from 2 853 810 cows) and reduced data cut off in 2011 (53 091 066 records from 2 502 307 cows). We used marker genotypes of 4480 bulls and 608 cows. Genomic enhanced breeding values (GEBV) of 305-day milk yield in all the lactations were estimated for at least 535 young bulls using two marker data sets: bull genotypes only and both bulls and cows genotypes. The realized reliability (R2) from linear regression analysis was used as an indicator of validation reliability. Using only genotyped bulls, R2 was ranged from 0.41 to 0.46 and it was always higher than parent averages. The very similar R2 were observed when genotyped cows were added. An application of ssGBLUP to a multiple-lactation random regression model is feasible and adding a limited number of genotyped cows has no significant effect on reliability of GEBV for genotyped bulls.
Introduction
Genomic selection using single-nucleotide polymorphism (SNP) information is an important tool for the genetic improvement of dairy cattle. The implementation of genomic selection as a substitute for progeny testing is expected to shorten the generation interval and lead to high genetic gain because genomic prediction is more reliable than parent averages (PA) by the traditional evaluation (Schaeffer 2006). That implies the accuracy of genomic evaluation is an important factor in the efficiency of genomic selection. Reliability of genomic evaluation depends on the number of genotyped animals with estimated breeding values (EBV) (Hayes et al. 2009; VanRaden et al. 2009). Improvement of reliability in genomic prediction is the challenge when the population has a limited number of genotyped animals.
Genotyped bulls with high reliability of EBV were usually used for reference populations. In Japan, about 200 progeny-tested proven bulls can be added as a reference population every year. In countries with few progeny-tested bulls such as Japan, increasing the genotyped bulls in the short term is difficult. Adding genotyped cows with phenotype can provide more reliable genomic prediction in such situations. Many researchers have reported the improvement of genomic prediction by adding genotyped cows (Ding et al. 2013; Cooper et al. 2015; Su et al. 2016). According to Su et al. (2016), the accuracy of validation cows had improved 3.9 points on average by including about 4800 cows to the population of about 1250 Danish and 1150 US bulls. The effect of genotyped cows was small when having a sufficient number of genotyped bulls in the reference population (Cooper et al. 2015). Only when the number of genotyped bulls is relatively small, using genotyped cows apparently seems to improve genomic prediction. In Japanese genomic evaluation, about 4000 genotyped bulls used as a reference population (National Livestock Breeding Center 2015), and using genotyped cows can lead the improvement of genomic prediction.
The current genomic evaluation system adopted in many countries is a multi-step procedure. The procedure has three steps: (1) traditional genetic evaluation; (2) estimation of direct genomic values (DGV) by SNP-BLUP (best linear unbiased prediction) or genomic BLUP (GBLUP) using a reference population; and (3) combining PA, DGV and PA from pedigrees of genotyped animals by selection index (VanRaden et al. 2009). Whereas this method has an advantage without changing a traditional genetic evaluation, there are many disadvantages: a calculation of pseudo-phenotypes such as de-regressed EBV (dEBV) or daughter yield deviations and needs of many parameters and assumptions in its computational process (Misztal et al. 2009; Aguilar et al. 2010). In addition, the multi-step procedure can cause a biased prediction due to using small genotyped populations with EBV (Patry & Ducrocq 2011). Legarra et al. (2009) and Misztal et al. (2009) proposed single-step GBLUP (ssGBLUP), with phenotypes, pedigrees and genotype data, which can resolve the aforesaid issues on the multi-step procedure and provide more reliable predictions (Tsuruta et al. 2013; Lourenco et al. 2014a). The ssGBLUP is also feasible when adding genotyped cows since the pre-adjustment of cow phenotypes is not required (Tsuruta et al. 2013).
In Japan, a multiple lactation random regression test-day model has been implemented in the traditional genetic evaluation of milk production traits (National Livestock Breeding Center 2015). There are few reports on application of ssGBLUP to such a complicated evaluation model with very large data sets in dairy populations. The objectives of this study were to evaluate a validation reliability of ssGBLUP for milk yield estimated with a random regression test-day model and to investigate an effect of genotyped cows on the reliability for Holstein bulls in Japan.
Materials and Methods
Data
Test-day records in the first three lactations from February 1975 to December 2015, which were collected by Hokkaido Dairy Milk Recording and Testing Association, were used in this analysis. Data editing for contemporary groups and number of records per cow per lactation was followed by Yamaguchi et al. (2015), who applied a random regression model for somatic cell score of Japanese Holstein cows. The number of records with full data was 60 850 534 from 2 853 810 animals. To validate reliability, reduced data were cut-off in 2011. Genomic enhanced breeding values (GEBV) and PA were estimated with reduced data. The number of records with reduced data was 53 091 066 records from 2 502 307 animals. Pedigree records in this analysis were collected by Holstein Cattle Association of Japan, Hokkaido-Branch. Table 1 shows numbers of records and pedigree animals for reduced and full data sets.
| Item | Data | |
|---|---|---|
| Reduced | Full | |
| First lactation | 20 994 117 | 24 197 663 |
| Second lactation | 18 124 656 | 20 774 346 |
| Third lactation | 13 972 293 | 15 878 525 |
| Total animals with records | 2 502 307 | 2 853 810 |
| Total pedigree animals | 3 020 252 | 3 396 012 |
A total of 4480 bulls and 608 cows were genotyped using Illumina BovineSNP50 BeadChip (Illumina Inc., San Diego, CA, USA). Table 2 shows numbers of genotyped bulls and cows by birth year. Genotyped cows had phenotype records in reduced data sets. In this analysis, GEBV were estimated with two marker data sets; (1) bulls only and (2) bulls and cows. As quality control of SNP, we conducted a minor allele frequency > 0.05, call rate > 0.90, and departures from Hardy–Weinberg equilibrium < 0.15. The number of SNPs permitted by these conditions was 35 821 in bulls only and 35 814 in bulls and cows.
| Birth year | Bulls | Cows |
|---|---|---|
| ≦1990 | 366 | |
| 1991 | 109 | |
| 1992 | 175 | |
| 1993 | 173 | |
| 1994 | 204 | |
| 1995 | 225 | |
| 1996 | 229 | |
| 1997 | 110 | |
| 1998 | 133 | 2 |
| 1999 | 139 | |
| 2000 | 180 | 3 |
| 2001 | 195 | 4 |
| 2002 | 182 | 8 |
| 2003 | 139 | 15 |
| 2004 | 218 | 26 |
| 2005 | 203 | 36 |
| 2006 | 198 | 82 |
| 2007 | 207 | 96 |
| 2008 | 206 | 162 |
| 2009 | 285 | 174 |
| 2010 | 305 | |
| 2011 | 299 | |
| Total | 4480 | 608 |
Statistical Model
A single-trait multiple lactation random regression model was used in this analysis; its model was an analogous model with national genetic evaluation in Japan (National Livestock Breeding Center 2015). The model was developed for test-day records in Hokkaido and included same effects as with Yamaguchi et al. (2015), except for the number of orders for fixed and random regression: fixed effects for lactation curve within herd test-year group-parity, lactation curve within calving month and lactation curve within calving age groups, and random effects for herd-test day-milking frequency, lactation curve for additive genetic and lactation curve for permanent environment. Legendre polynomials of first order for herd test-year group-parity and calving age groups, fourth order for calving month, and third order for additive genetic and permanent environment were used to model lactation curves. In addition, fixed lactation curves for herd test-year group parity and calving month were the combined Wilmink exponential function (Wilmink 1987). We calculated the evaluations for 305-day milk yields from the first three lactations and combined evaluation which averaged their evaluations. Heritability estimates of 305-day milk yield from the first three lactations were 0.420, 0.338 and 0.303, respectively, and their combined heritability by the same weighting was 0.464.
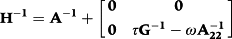
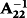is the inverse of the numerator relationship matrix for genotyped animals. The calculation of G was done by the first method proposed by VanRaden (2008). Then the allele frequency at each locus was calculated from current genotyped animals. The G can be singular and cannot be inverted. Therefore, G was blended as 0.95G + 0.05A22 to obtain a nonsingular matrix (VanRaden 2008). Subsequently, G was adjusted, that means of diagonals and off-diagonals for G were equal to those for A22 (Chen et al. 2011). The calculations of G, G−1 and
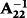were performed with LAPACK or BLAS using multi-threaded Intel Math Kernel Library (Aguilar et al. 2011). The τ and ω are the scaling factors for G−1 and
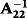, respectively (Tsuruta et al. 2011). The GEBV for animal i without phenotype records and progeny can be decomposed as shown in the following equation (VanRaden & Wiggans 1991):
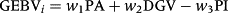
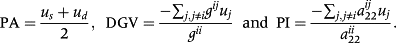
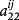are an element of G−1 and
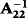for relationships between animal i and j, respectively (Aguilar et al. 2010; Lourenco et al. 2015). This means that τ and ω are the parameters to adjust contributions of DGV and PI, respectively. Appropriate weights of τ and ω can be different by the evaluated trait (Tsuruta et al. 2013; Koivula et al. 2015). The weights in this analysis were chosen from the result of our preliminary analysis by a lactation model, which investigated about 20 combinations of τ (1.0 or 1.5) and ω (from 0.1 to 1.0). In the preliminary analysis, a change of τ did not affect the reliability and inflation of GEBV as shown by Tsuruta et al. (2011). The smaller ω (less than 0.3) reduced prediction bias and had little effect on reliability. Based on this result, the weights of τ and ω in this analysis were set as 1.0 and 0.3, respectively.The MME in all the analyses were solved with iteration on data using preconditioned conjugate gradient (PCG) method (Tsuruta et al. 2001). The convergency criterion was set to 10−15 in all the analyses.
Validation of GEBV
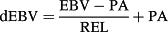
Results and Discussion
PCG rounds
Table 3 shows the number of PCG rounds for estimation of PA and GEBV from reduced data and EBV from full data. The ssGBLUP required additional rounds to converge, compared with traditional evaluation. These results were similar those of with Koivula et al. (2015) and Masuda et al. (2016). When adding genotyped cows, additional rounds were also required. The results of Masuda et al. (2016) reported that an increase of genotyped animals can cause lager computational rounds. A random regression model needs more computational rounds due to the complexity and large amount of records. To exclude old records may reduce computation costs, as Lourenco et al. (2014b) reported that the treatment did not affect the validation reliability for predictor animals.
| Data | Evaluation | Marker data | Convergence criterion | ||
|---|---|---|---|---|---|
| 10−13 | 10−14 | 10−15 | |||
| Reduced | PA | 2878 | 3706 | 4544 | |
| Reduced | GEBV | Only bulls | 3025 | 3694 | 4784 |
| Reduced | GEBV | Bulls and cows | 3112 | 3827 | 4879 |
| Full | EBV | 2826 | 4018 | 4353 | |
Validation reliability
Table 4 shows R2 and b obtained as the results of regression analysis for GEBV and PA from reduced data. The R2 from PA for first three and combined lactations ranged from 0.18 to 0.21. For GEBV, R2 ranged from 0.41 to 0.46 and were considerably higher than PA. The tendency of increasing R2 over lactations was observed. The regression coefficients of GEBV had much fewer biases than of PA. The values of R2 and b for GEBV when adding genotyped cows were similar with the results of only bulls.
| Lactation | No. of predictor animals | PA | GEBV | ||||
|---|---|---|---|---|---|---|---|
| Only bulls | Bulls and cows | ||||||
| R2 | b | R2 | b | R2 | b | ||
| First | 588 | 0.18 | 0.48 | 0.41 | 0.86 | 0.41 | 0.86 |
| Second | 574 | 0.18 | 0.50 | 0.43 | 0.92 | 0.43 | 0.92 |
| Third | 535 | 0.21 | 0.55 | 0.46 | 0.98 | 0.46 | 0.98 |
| Combined | 578 | 0.19 | 0.50 | 0.43 | 0.91 | 0.43 | 0.91 |
The ssGBLUP with the random regression model had higher R2, compared to traditional evaluations. Koivula et al. (2015) reported a similar result by applying the ssGBLUP to a multiple-trait (milk, fat, protein) random regression model. The weights of τ = 1.00 and ω = 0.30 in this analysis provided few biases (i.e. b was closer to 1), especially for GEBV from second, third and combined lactations. Koivula et al. (2015) investigated R2 and b by four combinations of τ and ω for milk traits, which had similar tendency in all the traits. Even only milk yield was validated in this analysis; putting same weights of τ and ω may lead to better results for the other milk traits. Tsuruta et al. (2011) concluded the use of common weight (τ = 1.00 and ω = 0.70) for all 18 linear type traits is suitable for US Holsteins. Further analysis is required to find the optimal weights for type traits of Japanese Holsteins. Since τ has a small effect on b (Koivula et al. 2015), the optimal ω should be investigated.
Increase of R2 in later lactations may be caused by the genetic evaluation model considered genetic correlation among lactations. Bauer et al. (2015) reported that the approximated reliability of GEBV for genotyped young bulls by ssGBLUP with multiple-trait test-day model between the first three lactations was highest in the second lactation. An implementation of the multiple-trait model improved R2 of the trait with a limited number of records (Guo et al. 2014; Bauer et al. 2015).
The validation reliability when adding genotyped cows was not different from using only genotyped bulls. There are several publications about the effect of using genotyped cows: Cooper et al. (2015) investigated contribution from 30 852 genotyped cows to the multi-step method for 28 US Holstein traits. The validation reliability for milk traits, which consists of milk yield, fat yield, protein yield, fat percentage and protein percentage, increased 0.4 points for validation bulls and 1.2 points for validation cows on average compared to the results from bulls only. The increase of all the traits was 0.4 points for validation bulls and 4.4 points for validation cows on average. When using only genotyped cows the validation reliability for all the traits improved 20 points to the traditional evaluation (PA) on average. Since the reliability for cows' EBV is lower than proven bulls, contribution from genotyped cows is small. Under the condition of a small number of genotyped bulls, the effect of genotyped cows was relatively large (Calus et al. 2013; Su et al. 2016). A further analysis with a larger number of genotyped cows may be required. Tsuruta et al. (2013) investigated the effect of adding genotyped cows by both the multi-step method and ssGBLUP for final scores. Although the small effect by using genotyped cows was found in either approach, the ssGBLUP had better predictions than the multi-step method. Tsuruta et al. (2013) indicated the possibility that cows with higher genetic merit were selectively genotyped and exposed to preferential treatment. In this study, 136 genotyped cows out of 608 were bull dams with high genetic merit. Therefore, the use of genotyped cows may lead to more biased GEBV. To resolve this problem, a pre-adjustment of cow phenotypes was implemented in the multi-step procedure (Wiggans et al. 2011, 2012). The ssGBLUP has an advantage of the simplicity of adding genotyped cows because the pre-adjustment of cow phenotypes is not required.
Genetic trends
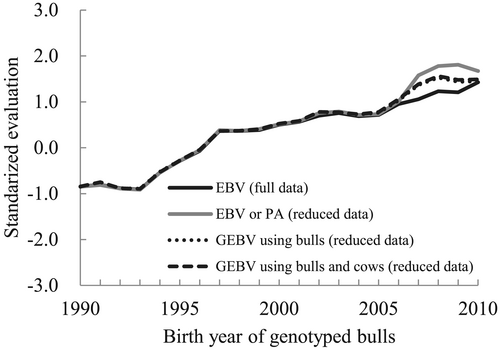
Figure 1 shows the genetic trends of genotyped bulls for EBV (PA) and GEBV from reduced data and EBV from full data for 305-day milk yield of combined lactations. These evaluations were standardized by subtracting the averaged EBV of cows born in 2005 and dividing by their standard deviation. The trend of PA during 2007 to 2010 from reduced data without marker information was overestimated, compared with EBV from full data. This overestimation of PA may have occurred due to the bull dams from Japan with overestimated EBV due to its lower reliability. In contrast, the bull dams from foreign countries did not apparently affect the overestimation of PA. However, their evaluations can also be biased predictions due to indirect estimation from only pedigree information (i.e. PA). Although the overestimated GEBV was found, the GEBV was less biased than PA and close to EBV. The trend of GEBV for genotyped bulls was not different from that for genotyped bulls and cows.
Conclusion
An application of ssGBLUP was feasible for a multiple-lactation random regression model. Adding a limited number of genotyped cows has no significant effect on reliability of genomic enhanced breeding values for genotyped bulls. In Japan, more than 20 000 females have been genotyped in the past few years. We need a further validation study with more genotyped cows.
Acknowledgments
The authors are grateful to Shogo Tsuruta (Department of Animal and Dairy Science, University of Georgia) for the helpful comments on this work.
