Bonding Heterogeneity and Nanoprecipitation on Substituting the Anionic Framework in Mg3Sb2 for p-Type Zintl Thermoelectrics
Abstract
Designing zintl compounds with complex crystal structures and large unit cells containing heavy elements may inherit bonding heterogeneity-induced lattice anharmonicity, leading to intrinsically low thermal conductivity. In this work, alloying-induced bonding heterogeneity in the extensively explored α-Mg3(Sb, Bi)2 phase due to local atomic ordering, site preferences, and prevailing heterogenous interfaces is evaluated in the p-type Mg3(Sb1−2xBixSnx)2-based polyanionic nanocomposites for different alloying concentrations. The inherent susceptibility for partial phase transition (trigonal → monoclinic) is observed upon alloying, which is driven by alterations in bonding patterns, localized distortion, and secondary phase formation. At low alloying content (x ≤ 0.05), a trigonal (Sb, Sn) phase is observed, while for higher alloying content (x ≥ 0.1), a cubic Mg2Sn nanophase emerges. A synergistic reduction in thermal conductivity and enhanced power factor maximize the zT ≈ 0.25(±0.05) at 673 K in the optimized p-type Mg3(Sb0.9Bi0.025Sn0.025)2 nanocomposites. The study highlights bonding heterogeneity-induced structural transitions as an inherent challenge, where the dominant role of anionic sites becomes pivotal for determining/deriving favorable structural and functional properties in Mg3(Sb, Bi)2-based zintl compounds.
1 Introduction
Low-grade waste heat recovery by thermoelectrics (TE) has garnered renewed attention in recent years, due to the outstanding n-type performance obtained in Mg3(Sb, Bi)2 solid solutions.[1-6] To complement this exceptional performance at the device level, ongoing efforts are aimed toward developing their low-cost and high-performance p-type counterpart, besides further optimization of their n-type TE figure of merit (zT) near room temperature.[7-9] Intrinsically, undoped Mg3Sb2 compound exhibits p-type conduction with a low hole concentration (n) ≈ 1017 cm−3 and a multivalley (Nv ≈ 6) conduction band behavior near the Fermi level.[10, 11] Upon heavy Bi alloying (≈25 at%) and subsequent doping by ≈1 at% with chalcogen group elements (i.e., Te, Se, S), a higher n ≈ 1019 cm−3 for n-type conduction was attained, leading to maximization of zT values ranging between 1.5 and 2 at ≈723 K for the optimized compositions.[1-4] Such high zT is comparable to, and even surpasses, many state-of-the-art n-type TE materials, leading to an impressive device performance with a conversion efficiency (η ≥ 7%) under a 300 K temperature difference (ΔT).[12, 13] Thus, the anionic framework constituting a covalently bonded network formed by complex anions or metalloids plays a vital role in sustaining the “electron–crystal” electronic structure in doped Mg3Sb2 crystals, which also exhibit an inherently low lattice thermal conductivity (κL) ≈1 Wm−1 K−1 near room temperature.[14-17]
As a prominent and widely explored zintl phase, Mg3Sb2 is part of the broader family of zintl antimonides, which encompasses diverse crystal structures and compositions, though only a small subset has been investigated for their TE properties.[18] On crystal structure basis, Mg3(Sb, Bi)2 and its mixed-anion derivatives are classified as 1–2–2 zintl family that exhibits CaAl2Si2-type structure (Space Group: Pm1, 164)[18-22] with an asymmetric unit cell having complicated bonds. Interestingly, Mg atoms reside in both the octahedrally coordinated interlayer Mg(I) site (i.e., the cation site) and the tetrahedrally coordinated intralayer Mg(II) site (i.e., within the anionic [Mg2Sb2]2− framework). The chemical bonding analysis of α-Mg3Sb2 indicates coordination flexibility of MgSb bonds having both ionic and covalent character, wherein covalent bonding in the [Mg2Sb2]2− anionic framework enables high carrier mobility, while the ionic Mg2+ cations offer better dopability for carrier concentration optimization.[10, 11] The site preference and occupancy patterns during the alloying/doping indicate that Mg(I) sites tend to be preferentially occupied by highly electropositive alkaline earth metals and lanthanides (such as Ca, Sr, Ba, La, and Yb), while Mg(II) sites exhibit a higher affinity for alloying with more electronegative metals like Zn, Mn, and Cd.[21]
Among its anionic solid solutions, Mg3Sb2−xBix and its derivatives exhibit an excellent bandgap tunability which has allowed optimization of n-type properties by reducing the bandgap to enable efficient doping efficiency with Te/Se/S as dopants.[1-4] However, for p-type conduction, anionic doping strategies (i.e., substituting dopants on the Sb/Bi sites) in Mg3(Sb, Bi)2 and its related solid solutions have remained largely ineffective,[23-26] primarily due to its weak valence band degeneracy (Nv = 1).[27] Nevertheless, codoping approaches (Zn, Na, Yb, Ag, and/or Cu)[28-32] primarily targeting the cationic Mg(I) and/or anionic Mg(II) sites have remained effective in regulating and optimizing holes concentration, reaching an optimal n ≈ 1019 cm−3 to attain a maximum zT ≈ 0.8 at around 773 K.[28-33] From a practical perspective, enhancing the TE performance of p-type Mg3(Sb, Bi)2 to match its n-type counterpart still remains critical and an ongoing challenge for realization of the α-Mg3Sb2-based device, with a maximum conversion efficiency (η) ≈5.5% at the hot-side temperature of 573 K, reported till date.[34]
Complex multinary zintl compounds constituting a polyanionic (ternary, quaternary, and higher) framework can offer new basis for deriving novel functionalities and understanding of the poor dopability of p-type Mg3(Sb, Bi)2. We report Mg3(Sb1−2xBixSnx)2-based polyanionic nanocomposites with bonding heterogeneity-induced locally distorted structures and nanoprecipitation, synthesized employing ball milling and spark plasma sintering. The preferences for specific site occupancies of (Bi, Sn) substitutions in Mg3Sb2 were assessed employing a (3 + 1) dimensional superspace approach, which provided critical insights into the atomic-scale interactions and local atomic ordering in the constituting α-Mg3Sb2 phase. Partial phase transition (trigonal → monoclinic), nanoprecipitation of trigonal (Sb, Sn, Bi) phase for low alloying content x ≈ 0.05, and Mg2Sn nanoprecipitation for increasing alloying content x > 0.05, was observed implying locally distorted structures. The present study highlights the inherent susceptibility of Mg3(Sb, Bi)2-based polyanionic solid solutions for bonding heterogeneity, structural transitions, and secondary phase formations and their implications on thermal and electrical transport properties. It also demonstrates how alloying strategies require vital consideration of structural and bonding modifications to effectively attain better dopability and targeted functionalization of transport properties of zintl compounds.
2 Results and Discussion
2.1 Phase Compositions, Phase Segregation, and Hierarchical Microstructure
The powder diffraction X-ray diffraction (PXRD) patterns of representative Mg3(Sb1−2xBixSnx)2 nanocomposite samples are shown in Figure 1a, which indicate major peaks corresponding to trigonal α-Mg3Sb2 phase (Space Group : Pm1, 164) in all the alloyed compositions. For low alloying content x ≈ 0.05, additional peaks corresponding to the trigonal (Sb, Sn, Bi) phase (Space Group: Rm, 166) were also indexed and indicated by star (*), while for higher alloying content x ≥ 0.1, peaks corresponding to cubic Mg2Sn phase (Space Group: , 225), as indicated by inverted triangle (
), appear, implying α-Mg3Sb2 phase instability and secondary phase precipitation process during synthesis. With increasing equiatomic (Sn, Bi) content, that is, x, the major and overlapping (101) and (011) PXRD peaks shift to lower angles (Figure 1b) when compared with synthesized Mg3Sb1.9Sn0.1, suggesting an expansion of the α-Mg3Sb2 lattice. In addition to lattice expansion, shifts in major overlapping peaks can be attributed to secondary-phase formation, potentially altering the Sb/Bi ratio in the synthesized nanocomposites. Beyond x ≥ 0.2, additional peaks corresponding to tetragonal Sn phase (Space Group: I41/amd 141) indicated by an empty inverted triangle (
) were also observed. Samples with higher alloying content are also more chemically stable, during unavoidable exposure to atmospheric conditions during XRD measurements, as indicated by absence of MgO impurity peaks, which is distinctively observed for x ≈ 0.05 and indicated by filled circles. The presence of extra peaks corresponding to secondary phases even in synthesized Mg3Sb1.9Sn0.1 is indicative of the discordant nature of Sn/Sb atoms in MgSbSn-based compositions, wherein secondary-phase precipitation was also observed.[35-37] Notably, the synthesized Mg3(Sb1−2xBixSnx)2 compositions lie well within the solid solubility limits of Bi (i.e., x ≈ 0.4)[23] for Mg3Sb2−xBix and agree well with the previous structural observations reported for Mg3Sb2−xSnx polycrystals.[36]
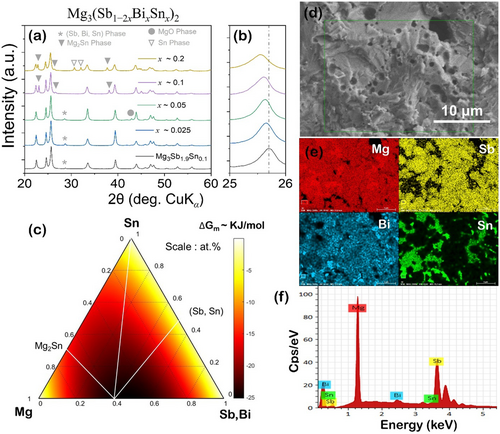
To understand phase stability, potential phase transformations, and optimal compositions in the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites, ternary phase diagram of MgSbSn at room temperature (an isothermal section)[35] is overlaid over the evaluated modified Gibbs free energy of mixing and is shown in Figure 1c. Previous investigation has revealed the observed difficulty in synthesizing ternary MgSbSn compounds,[35-38] wherein binary α-Mg3Sb2 compound was evaluated[35] to coexist with Mg2Sn, Sn, and SnSb in phase equilibria. The Gibbs free energy of mixing (ΔGm) landscape influences the extent of solid solution formation, where the lowest ΔGm implies thermodynamic stability, in regions corresponding to the synthesized compositions. The secondary-electron scanning electron microscopy images presented in Figure 1d display backscattered electron (BSE) micrograph of characteristic fracture surface morphology i a representative sample, indicative of transgranular fracture. This fracture mode is characterized by crack propagation occurring through the grains rather than along grain boundaries. The fracture surfaces reveal prominent cleavage facets with aligned lamellae patterns, which are characteristic of plastic deformation within individual grains. The nanoprecipitation promotes local ordering, contributing to the development of layered structures that accommodate anionic substructures. Consequently, the material's response to stress likely involves both grain-level plasticity and substructural adjustments, leading to the observed layered morphology.[39]
The presence of nanoinclusions within the microstructure can be attributed to localized compositional variations caused by the discordant Sn atoms, which nucleate and segregate from the supersaturated Mg3(Sb, Bi)2 solid solution as indicated by elemental mapping shown in Figure 1e. The energy-dispersive X-ray (EDX) spectrum shown in Figure 1f, confirms the existence of an extended solid solution comprising Mg2Sn, Bi, and SnSb within the Mg3Sb2 matrix, agreeing well with the previously reported phase equilibria studies in the MgSbSn system.[35] Thus, a complex interplay between the different phases in the heterogeneous microstructure with nanoscale features of the synthesized nanocomposites is indicative of the structural differences between Mg2Sn and Mg3Sb2 phases that preclude the formation of a complete solid solution agreeing well with previous observations.[37, 38]
2.2 Structural Parameters and Monoclinic Phase Transitions
Substitutions at the anionic framework in zintl phases are highly susceptible to causing structural distortions, which may result in lowering of symmetry, changes in bonding patterns, and formation of monoclinic variants.[18, 21, 22, 40] These distortions are often driven by electronic factors or size differences between substituted atoms.[26] In the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites, an extensive structural disorder with a partial loss of trigonal symmetry leading to monoclinic phase transitions (Space Group: C2/m, 12) was also indexed during refinement, implying a locally distorted configuration and chemical disordering in the synthesized polycrystals. It is noteworthy that the observance of monoclinic structure in the synthesized polycrystals as a highly distorted variant owes structural similarity to the high-pressure monoclinic structure for Mg3Sb2 and Mg3Bi2 reported previously at critical transition at above 7.8 and 4.0 GPa, respectively.[41] However, the synthesized polycrystals exhibit an irreversible and co-existing monoclinic phase as shown in Figure 2a, in contrast to the pressure-induced displacive and reversible (trigonal ↔ monoclinic) phase transition, reported previously.[41] The refinements of the PXRD evaluates the monoclinic C2/m unit cell (formula unit = 6) with a volume per formula unit of ≈500 Å3.
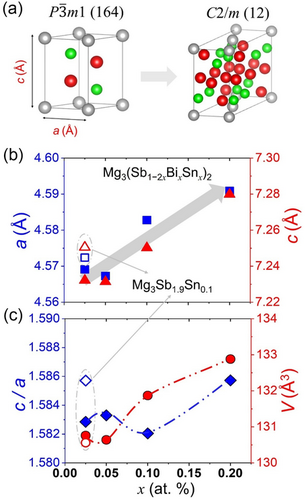
The refined lattice parameter of the α-Mg3Sb2 phases, as shown in Figure 2b, obtained by Le Bail refinement, reveals an initial decrease in lattice parameters a and c for lower alloying content, followed by a consistent increase with higher alloying levels. The refined XRD patterns are shown in Figure S1–S3, Supporting Information, which displays the observed, calculated, and difference profiles along with the Bragg peaks of the constituting phases and refinement parameters are tabulated in Table 1. The Sn, Bi dissolution into the Mg3Sb2 matrix, particularly of Bi atoms within the α-Mg3Sb2 phase, implies accordance with Vegard's Law. However, even for low alloying content, that is, x ≤ 0.05, complex coordination and trigonal (Sb, Sn, Bi) phase precipitation may result in α-Mg3Sb2 phase lattice contraction. For the higher alloyed compositions, that is, x ≥ 0.1, cubic Mg2Sn phase precipitation and larger elemental volume of Bi in comparison to Sb atoms led to larger and increasing lattice parameter a and c, implying dopant solubility in the constituting phases. When Sn is introduced at Sb site, it occupies specific anionic sites (causing Sb atoms precipitation), leading to alterations in the local lattice environment and symmetry of α-Mg3Sb2 phase. Thus, the average crystal structure of the synthesized Mg3(Sb1−2xBixSnx)2 polycrystals and stability of constituting phases are related to the amount of dopant, besides the differences in the atomic size and electronegativity of the host and substituted Sb anions. It is worth mentioning that the presence of excess Mg at cationic sites can stabilize or destabilize certain phases, potentially promoting or preventing the monoclinic phase transitions. In contrast to the anisotropic structural collapse with relative compression of the a and c-axes,[41] the monoclinic phase formation is accompanied by unit cell expansion of α-Mg3Sb2 unit cell. The alloying content dependence of the c/a ratio and unit cell volume of the major trigonal α-Mg3Sb2 phase, as shown in Figure 2c, reveals a more elongated unit cell for higher alloying content, with varying c/a ratio. When compared to doped Mg3Sb1.9Sn0.1, codoping Sn and Bi atoms causes a reduction in the c-axis length relative to the a-axis, which can be ascribed to instability and partial loss of symmetry of major α-Mg3Sb2 phase. As the volume increase is significant, it is indicative of dopant solubility and a growing potential for precipitation of secondary phases at higher alloying contents, discussed subsequently. The partial loss of trigonal symmetry in the synthesized Mg3(Sb1−2xBixSnx)2 by phase transition occurs at the anionic [Mg2Sb2]2− framework and can be ascribed to the discordant Sn atoms, preferentially occupying specific lattice sites in the alloyed polycrystal. The expanding unit cell volume for trigonal phase is indicative of a displacive phase transition wherein the distorted coordination polyhedral within the anionic framework may constitute bonding heterogeneity.
| Compositiona) | Space group | Lattice parameters | Volume | R-factorsb) | ||
|---|---|---|---|---|---|---|
| GOF | ||||||
| Mg3Sb1.9Sn0.1 | P m1 | a = b = 4.5724(1), c = 7.2505(2), α = β = 90°, γ = 120° | 130.56(1) | 1.59 | 3.76 | 5.12 |
| C2/m | a = 14.493(1), b = 4.396(1), c = 7.908(1), α = γ = 90°; β = 90.858(3) | 503.74(1) | ||||
| R m | a = b = 4.303(1), c = 11.335(1), α = β = 90°, γ = 120° | 181.80(1) | ||||
| x ≈ 0.025 | P m1 | a = b = 4.5691(1), c = 7.2322(2), α = β = 90°, γ = 120° | 130.76(1) | 1.63 | 3.65 | 5.05 |
| C2/m | a = 14.413(1), b = 4.348(1), c = 7.873(1), α = γ = 90°; β = 90.907(6) | 493.38(1) | ||||
| R m | a = b = 4.299(1), c = 11.300(3), α = β = 90°, γ = 120° | 180.92(1) | ||||
| x ≈ 0.05 | P m1 | a = b = 4.5673(1), c = 7.2314(1), α = β = 90°, γ = 120° | 130.64(1) | 1.55 | 3.38 | 4.80 |
| C2/m | a = 14.452(1), b = 4.340(1), c = 7.866(1), α = γ = 90°; β = 91.013(5) | 493.35(1) | ||||
| R m | a = b = 4.317(1), c = 11.307(2), α = β = 90°, γ = 120° | 182.51(1) | ||||
| x ≈ 0.1 | P m1 | a = b = 4.5828(1), c = 7.2502(2), α = β = 90°, γ = 120° | 131.87(1) | 1.72 | 4.02 | 5.30 |
| C2/m | a = 14.517(1), b = 4.463(1), c = 7.935(1), α = γ = 90°; β = 90.606(6) | 503.74(1) | ||||
| Fm m | a = b = c = 6.6795(2), α = β = γ = 90° | 298.01(1) | ||||
| x ≈ 0.2 | P m1 | a = b = 4.5909(1), c = 7.2799(3), α = β = 90°, γ = 120° | 132.88(1) | 1.34 | 3.00 | 3.91 |
| C2/m | a = 14.581(1), b = 4.496(1), c = 7.998(1), α = γ = 90°; β = 90.847(5) | 524.29(2) | ||||
| Fm m | a = b = c = 6.7477(2), α = β = γ = 90° | 307.24(1) | ||||
| I41/amd | a = b = 5.8287(2), c = 3.1798(2), α = β = γ = 90° | 108.03(1) | ||||
- a) Space group, lattice parameters, unit cell volume (Å2), and refinement parameters (weighted profile (Rwp); profile (Rp); and expected (Rexp) R-factor). Standard deviations are given in parentheses.
- b) .
2.3 Bonding Heterogeneity and Low Thermal Conductivity
Mixed-anion compounds, which contain polyanions as separate building blocks, may result in locally distorted structures where more than one anion bonds to a cation. The bonding environment in Mg defect complex, particularly the coordination and geometric arrangement of Mg and Sb atoms, contributes to its overall stability or functionality. In the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites, the formation of MgSb6 octahedra and MgSb4 tetrahedra as well as their interactions through shared corners and edges to prevailing nanoclusters was understood by evaluating bond lengths and occupancies in the trigonal α-Mg3Sb2 phase, a polar intermetallic phase. The Mg(I)Mg(II) distances in Mg3Sb2 are ≈3.736 Å, while the MgSb distances range from about 2.8 to 3.2 Å.[11] Particularly, Mg(I)Sb is slightly longer than Mg(II)Sb, suggesting that both MgMg and MgSb interactions are significant in α-Mg3Sb2. The Mg(I) atoms are coordinated by six Sb atoms in a trigonal prismatic arrangement, while Mg(II) atoms are tetrahedrally coordinated by four Sb atoms as shown in Figure 3a. The bonding in Mg3Sb2 is predominantly ionic with some covalent character in the MgSb interactions,[42] wherein the Mg(I)Mg(II) interactions, while present, are relatively weaker than the MgSb bonds.
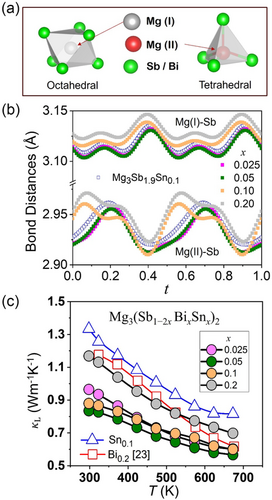
To evaluate bonding heterogeneity, positional modulation of the atomic sites was introduced, after several refinement cycles, considering isotropic displacement parameters up to the fourth order of the Fourier terms An and Bn (n = 1–4) using both cosine and sine components. The anion 4b Wyckoff site is occupied by the Sb and Mg(II) atoms whereas the cation 4a Wyckoff site is occupied by Mg(I) atoms, as shown in Figure 3b. The presence of three anions (i.e., Sb, Sn, and Bi) at the 4a Wyckoff site in (Mg2Sb2−2xBixSnx)2− motifs may result in an enhanced degree of anionic disorder in the trigonal α-Mg3Sb2 phase leading to locally distorted configurations with partially broken symmetry. The altering bonding distances of octahedral Mg(I) and tetrahedral Mg(II) environments, ranging from 2.87 to 3.02 Å, for lower (x ≤ 0.05) and higher (x ≥ 0.1) substitution, suggest compressibility and expansion, respectively. Softer and longer Mg(I)(Sb, Bi, Sn) bonds reveal an initial decrease and subsequent increase in bond length, corroborating well with the decreasing and increasing lattice parameter c, respectively. Remarkably, a similar trend for the shorter Mg(II)(Sb, Bi, Sn) bonds constituting the polyanionic framework was evaluated, wherein an altering bonding patterns was also evaluated for higher (x ≥ 0.1) substitution in the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites. Interestingly, atomic displacement evaluated for trigonal α-Mg3Sb2 and shown in Figure S7, Supporting Information, indicates a significant variation for Mg(II) and Sb atoms constituting the anionic framework for varying alloying content. Thus, synthesized Mg3(Sb1−2xBixSnx)2 constituting polyanionic framework is bound to have bonding heterogeneity-induced localized distortion and secondary phase formation with altered bonding lengths. A comprehensive understanding of bonding heterogeneity and structural transitions requires integrating advanced techniques such as atom probe tomography,[43-45] nuclear magnetic resonance,[43] X-ray photoelectron spectroscopy,[46] high-resolution transmission electron microscopy,[45-48] and Raman spectroscopy,[46, 47] which should be the focus of future research to explore local atomic and electronic environments. Moreover, interfacial lattice matching analysis[49] can be used in conjunction with crystal orbital Hamilton population evaluations[50] to study the compatibility and interactions between different phases at their interfaces.
The constituting locally distorted structures with a diverse bonding environment in mixed-anion Mg3(Sb1−2xBixSnx)2-based nanocomposites are anticipated to result in significant variations in interatomic force constants, splitting of phonon frequencies, and enhanced anharmonicity when compared to single-anion Mg3Sb2.[51] The locally distorted structures resulting from altered coordination numbers (CN) in mixed-anion materials introduce bonding heterogeneity, which effectively contributes to achieving low κL as indicated in Figure 3c. The Sn atoms preferentially occupy lattice sites with distorted square prismatic coordination (CN ≈ 8, Fm-3m), distinct from the monocapped trigonal prismatic sites (CN ≈ 7, P-3m1) typically occupied by the substituted host Sb atoms in the anionic framework, leading to bond heterogeneity. Moreover, higher dopant solubility at the polyanionic framework enhances scattering of phonons by mass/strain fluctuations particularly for lower substitution.
Despite Sn limited solubility, a pronounced phonon scattering was attained, thus lowering the κL to >30% in comparison to Bi-[23] and Sn-doped Mg3Sb2 counterparts in the measured temperature range. In Mg3(Sb1−2xBixSnx)2-based nanocomposites, κL decreases from ≈1.35 Wm−1 K−1 (Mg3Sb1.9Sn0.1) to ≈0.9 Wm−1 K−1 (x = 0.05) at 298 K, implying enhanced scattering of lower-frequency phonons. The limited dopant solubility and coexisting secondary phases in the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites have contrasting effects on κL: wherein heterogeneous interfaces (presumably Mg3Sb2Mg2Sn)[37, 38] instead of enhancing phonon scattering apparently decrease interfacial thermal resistance, resulting in higher κL. Furthermore, higher κL is evaluated for higher alloying content x ≈ 0.2, where undesirable (Sn/SnSb) phases evolve, violating the T−1 temperature-dependent κL more drastically, thereby compensating the phonon scattering occurring at heterogeneous interfaces.[17] Thus, thermal transport indicates critical role of structural inhomogeneity, bonding heterogeneity, and phase separation in increasing the lattice anharmonicity, which is effective in reducing κL of the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites.
2.4 Electronic Band Structure, Ionized Impurity Scattering Mechanism, and zT Enhancement
The Mg3(Sb, Bi)2-based zintl compounds exhibit a complex band structure with a challenging large and asymmetric unit cell.[11, 52] Similar to state-of-the-art (Sb, Bi)2Te3 alloys, electronic band structure of Mg3(Sb, Bi)2 constitutes low-symmetry conduction band minimum (CBM) with high band degeneracy (Nv ≈ 6). However, low band degeneracy (i.e., Nv ≈ 1) of valence band maximum (VBM) limits the optimization of power factor for p-type conduction.[27] Notably, transitioning from semiconductor-to-metallic behavior occurs on varying the Sb content Mg3Sb2−xBix with minimum κ measured for x ≈ 0.5.[14] To simulate and analyze the effects of disorder on the electronic band structure of the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites, Korringa-Kohn-Rostoker (KKR) -coherent potential approximation (CPA) approach is employed which replaces the actual disordered crystal structure with an effective medium Green's function and a self-energy.[53-55] Even at low doping levels, the KKR-CPA approach provides a realistic representation of the disordered doped system without necessitating large supercells,[56-59] making it particularly relevant for our evaluation of (Sn, Bi) codoped Mg3Sb2. The electronic band structure with estimated spectral weight variations corresponding to Bloch spectral functions (BSFs) in arbitrary units (a.u.) of Mg3Sb1.9Sn0.1 and Mg3Sb1.8Sn0.1Bi0.1 is shown in Figure 4a,b, respectively.
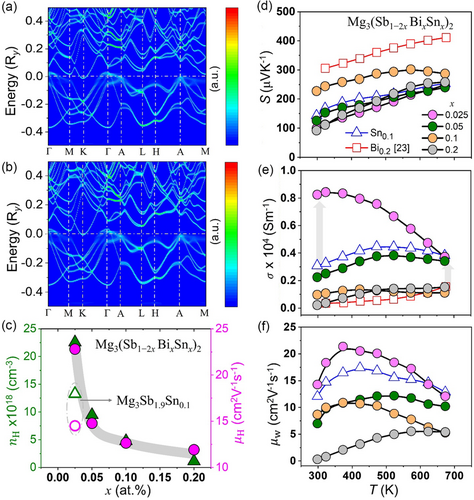
The band dispersion shows notable changes upon Sn doping, with the VBM at the Γ point and the CBM at the K point, agreeing well with the evaluation made previously employing supercell approach.[36] Since the VBM and CBM are located at different points in k-space (Γ and K, respectively) with coinciding energies, the resulting zero indirect bandgap allows carriers to undergo transition from the valence to the conduction band without a change in momentum, but via an intermediate state. Diffused spectral weight and overlapping bands at the Γ and A points in the valence band suggest that electronic states are spread over a range of energies implying disorder, impurities, or strong electron–electron interactions. The upward shift of the VBM points to an enhanced p-type conductivity, indicating metallic or semimetallic behaviour due to the zero indirect bandgap and band overlap. Previous calculations have also suggested the VBM of Mg3Sb2 at the Brillouin zone center (Γ) being dominated by the p orbitals of Sb anions that are composed of in-plane px,y and out-of-plane pz orbital.[2, 36, 60] Furthermore, the reduction in σ(T) upon Bi codoping could be well associated with a pronounced chemical disorder which enhances carrier scattering in the (Mg2Sb2−2xBixSnx)2− motifs. The negative bandgap, accompanied by an upward shift of the valence bands, indicates enhanced interactions between electronic states, while an increased orbital overlap may spatially confine electrons, reducing the density of free charge carriers in the system.
To understand carrier characteristics, Hall measurement results at room temperature are shown in Figure 4c. The Mg3(Sb1−2xBixSnx)2 nanocomposites for x ≈ 0.025 reveal a significant increase in both carrier mobility (μH) and carrier concentration (nH), in comparison to synthesized Mg3Sb1.9Sn0.1, which can be ascribed primarily to the upshift of VBM. However, with increasing substitution, decreasing nH and deteriorating μH were measured, attributed to an enhanced carrier scattering. The effects of Sn and Bi substitutions on temperature-dependent electrical transport behavior of the synthesized Mg3Sb1.9Sn0.1 and Mg3(Sb1−2xBixSnx)2 nanocomposites are shown in Figure 4d–f, alongside the previously reported Mg3Sb1.8Bi0.2 for comparison.[23] The temperature-dependent Seebeck coefficient S(T), shown in Figure 4d, implies p-type conduction, as also corroborated from the Hall measurement data. At room temperature, S for Mg3Sb1.9Sn0.1 (≈143 μV K−1) increases linearly with temperature, reaching a value of ≈253 μV K−1 at 673 K. As the cosubstitution of Sn and Bi increases, the Seebeck coefficient at room temperature shows a marginal decrease for x ≈ 0.25, likely due to changes in the carrier concentration or scattering mechanisms. However, for phase-separated sample x ≈ 0.1 having heterogeneous interfaces (presumably Mg3Sb2Mg2Sn), S increases to ≈227 μV K−1 at 300 K and decreases thereafter, which can be ascribed primarily to carrier filtering.
The temperature-dependent electrical conductivity σ(T) within the temperature range of 300–673 K shown in Figure 4e indicates a significant increase in σ(T) for x ≈ 0.25 to a measured value of ≈8.2 × 103 S m−1 at room temperature, corresponding to ≈1.6-fold enhancement over Mg3Sb1.9Sn0.1 (≈3.1 × 103 S m−1), which agrees well with the values reported previously.[36] This increase is primarily due to the introduction of additional charge carriers by Sn substitution. However, with (Sn, Bi) cosubstitution, σ(T) decreases as a result of additional scattering centers (reducing carrier mobility), primarily due to increasing phase fractions of secondary phases, which reduce carrier mobility. Additionally, modifications in the band structure by Bi substitution are likely contribute to this decline in electrical conductivity, as observed previously in Mg3Sb1−xBix.[23] The σ(T) of phase-separated nanocomposites at higher alloying content aligns with the σ(T) of Mg3Sb1−xSnx reported previously and implies the detrimental effects of phase separation on electrical conductivity.[36] This suggests that the presence of segregated phases leads to increased scattering and reduced μH ultimately compromising the electrical transport for higher substitutions.
The weighted mobility (μw)[61] derived S(T) and σ(T) measurements, that closely mirror μH, are also shown in Figure 4f as it reflects electron mobility weighted by the density of electronic states, providing insights into the electronic structure and scattering mechanisms. The observed increase in μw with temperature suggests ionized impurity scattering as the primary mechanism of carrier scattering. At lower temperatures, slower carriers allow more interactions with charged impurities, while as temperature rises, carriers move faster, reducing scattering from ionized impurities and thus increasing μw. However, at higher temperatures, mobility typically decreases due to increased lattice vibrations (phonon scattering), indicating the coexistence of multiple scattering mechanisms, each varying in influence with temperature and alloying content.
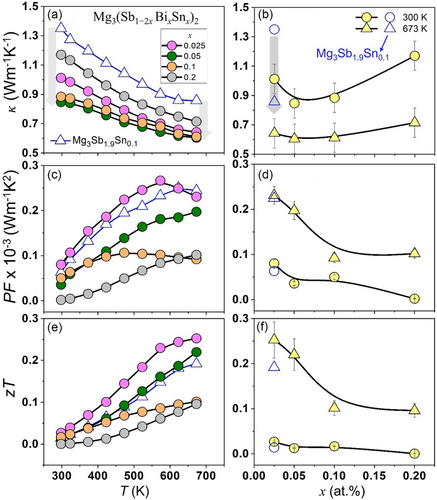
The temperature-dependent thermal conductivity κ(T) shown in Figure 5a also indicates significant reduction in Mg3(Sb1−2xBixSnx)2 nanocomposites, in comparison to Bi-[23] and Sn-doped Mg3Sb2 counterparts ascribed primarily to lattice anharmonicity, phase separation, and dynamic structural disorder. κ(T) is significantly lowered even for low alloying content as shown in Figure 5b, when compared to Mg3Sb1.9Sn0.1 both at low (≈300 K) and high (≈673 K) temperature. The increase in κL for x > 0.05 can be attributed to the higher κ of the Mg2Sn phase[62] and Sn segregation, which presumably enhances the phonon propagation by creating additional thermally conductive pathways. The power factor (Figure 5c,d) shows a marginal deterioration compared to Mg3Sb1.9Sn0.1 for low alloying content (x ≤ 0.05) and decreases significantly thereafter with increasing alloying content, primarily to reduction in both S(T) and σ(T) due to secondary phase formations. However, the enhancement is more significant in relation to Mg3Sb1.8Bi0.2,[23] for lower temperatures (<600 K), achieving a maximum power factor of ≈2.5 μW cm−1 K−2 at 573 K, thus, implying that the cosubstitution of Sn and Bi sustains the power factor for low alloying content (x ≤ 0.05) and remains detrimental for increasing substitution (x ≥ 0.1) due to Mg2Sn phase precipitation. The zT shown in Figure 5e for all the synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites increases with temperature, wherein Mg3Sb1.9Sn0.1 exhibits significantly higher zT ≈ 0.2 (± 0.05), which increases marginally for x ≈ 0.25–0.5 (as shown in Figure 5f), primarily due to a notable κ reduction, thus, demonstrating that (Sn, Bi) substitutions effectively improve the zT, but inherent distortion and phase separation prove detrimental to further enhance the zT, which optimizes only for lower content (x ≤ 0.05) in synthesized Mg3(Sb1−2xBixSnx)2 nanocomposites.
Thus, a limited understanding of structural changes that occur during doping or alloying hinders insights into their prominent effects on conduction/valence bands and defect chemistry. While challenges such as limited solubility and poor doping efficiency persist, improving carrier mobility and power factor in p-type Mg3Sb2 necessitates exploring codoping or alloying, especially within the anionic framework along with effective cationic dopants such as Na, Yb, Ag, Zn, and/or Cu.[28-32] Thus, complex multinary p-type Mg3(Sb,Bi)2-based zintl nanocomposites, with polyanionic frameworks, offer potential for realizing all-Mg3Sb2-based TE devices with enhanced TE conversion efficiency. However, addressing intrinsic monoclinic phase transition, nanoprecipitation susceptibility, and bonding heterogeneity remains critical for optimizing transport properties.
3 Conclusion
Anionic solid solutions constituting a polyanionic substructure can offer a versatile approach to favorably tune p-type conduction in Mg3(Sb, Bi)2 by regulating the composition of the anionic framework. The synthesized (Sn, Bi) cosubstituted Mg3Sb2-based polyanionic solid solutions exhibit bonding heterogeneity in dominant α-Mg3(Sb, Bi)2 phase, intrinsic partial monoclinic phase transitions, and nanoprecipitation susceptibility with varying alloying content. Coexistence of different crystal structures and phases relays poor dopability and limited solubility, highlighting the critical role of anionic framework for phase stability. Despite low content (x ≤ 0.05), structural changes induced by (Sn, Bi) substitution reduce κ and synergistically enhance carrier mobility and concentrations, leading to improved power factor and zT. Phase separation of cubic Mg2Sn for higher alloying content (x ≥ 0.1) enhances κL and deteriorates carrier transport, thereby drastically reducing the zT. Thus, alloying/substitution strategies must carefully account for structural and bonding modifications to enhance dopability and tailor the transport properties of zintl compounds.
Acknowledgements
This research was supported by JST Mirai Program, Japan (grant no. JPMJMI19A1).
Conflict of Interest
The authors declare no conflict of interest.
Author Contributions
Nagendra Singh Chauhan: conceptualization (equal); formal analysis (lead); investigation: (lead); methodology (lead); writing—original draft (lead). Takao Mori: conceptualization (equal); funding acquisition (lead); project administration (lead); resources (lead); supervision (lead); writing—review and editing (lead).
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
