Exceptional Hydrogen Diffusion Rate over Ru Nanoparticle-Doped Polar MgO(111) Surface
Abstract
Hydrogen (H) conductivity on oxide-based materials is crucially important in fuel cells and related catalysis. Here, this work measures the diffusion rate of H generated from Ru nanoparticles loaded on polar MgO(111) facet particles under H2 at elevated temperatures without moisture and compares it to conventional nonpolar MgO(110) for the first time by in situ quasielastic neutron scattering (QENS). The QENS reveals an exceptional diffusion rate on the polar facet via a proton (H+) hopping mechanism, which is an order of magnitude superior to that of typical H+-conducting oxides. This work attributes this to the unique atomic arrangement of alternate layers of Mg cations and O anions of the polar MgO(111) where the strong electrostatic field of terminal oxygen anions facilitates protonic migration with a lower degree of local covalency.
1 Introduction
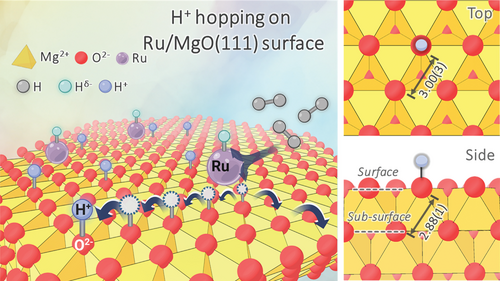
Diffusion of hydrogen (H) on solid surfaces at elevated temperature under gas phase hydrogen (H2) plays a key role in a broad range of chemical processes, especially in energy storage, fuel cells, and catalysis.[1-5] One of the most recognized phenomena is the so-called “H spillover” by which surface activated H atoms migrate from a H-rich metal cluster(s) to the surface of a catalyst support without homolytic dihydrogen dissociation.[1, 4, 6] Despite the fact that various researches on this mechanism have been published, its nature, catalytic functions, and even existence remain the subject of hot debate. This is due to a dearth of model catalysts capable of providing direct evidence of H spillover and simplifying catalytic interpretation. Given that each facet of a crystallite possesses distinctive intrinsic energy and atomic arrangement of a support, tailoring support particle physiochemical properties by exposing a particularly high energy polar oxide facet with the termination of entire oxygens or cations has recently attracted a significant attention.[7] Transition metal nanoparticle supported on polar MgO(111) is claimed to display higher hydrogenation activity than nonpolar facets and we also reported a substantial enhancement in ammonia production rate over Cs doped Ru/MgO catalyst from N2/H2 by replacing the polycrystalline MgO with electrostatically polar MgO (111) facet support.[2] From kinetic analysis, the polar MgO(111) support could mitigate the strongly adsorbed H on the overlying Ru nanoparticles (H poisoned metal surface) to uptake nitrogen at a higher rate by reversibly transferring the H to the support surface during catalysis. Recently, it is also evident that H2 is activated by the catalyst via a frustrated Lewis pair of Ruδ+-Oδ− at the Ru/MgO(111) interface to generate protonic H species on MgO(111) to facilitate their migration on the support material (Figure 1).[3] The interchangeable status of H, proton (H+), and hydride (H−) is rigorously described and presented. These observations can help us better understand H storage and catalytic reactions involving H. However, the dynamics of the H migration over the catalyst surfaces still remain unclear and extremely difficult to observe experimentally on atomic length scales. This is especially true for light molecules with a limited number of electrons, such as H. Thus, it is of importance to probe the diffusion of H over the surface of Ru-doped polar metal oxide materials using high-resolution equipment having the ability to detect the dynamics of such a light element under realistic conditions.
Among several dynamics probing techniques, quasielastic neutron scattering (QENS) enables the detection of molecule displacements in time and space, from pico- to tens of nanoseconds and from Ångströms to nanometers, respectively. The technique investigates dynamics ranging from fast vibrational modes down to slow diffusive motion. Each scattering experiment produces a dynamic structure factor S(Q,ω) or its spatial and temporal Fourier transform (van Hove correlation function G(r, t). This depicts where the atoms are and how they move. A key strength of QENS is its extreme sensitivity to H motions due to a significantly larger incoherent cross-section of the H atom (80.26 barns, where 1 barn = 10−24 cm2) compared to all other scattering cross-sections. This renders QENS to be one of the most powerful tools to study diffusion in which H is involved.
Herein, we investigate and compare the H mobility across the Ru-based MgO surfaces for the first time including Ru/MgO(111) and Ru/MgO(110) in the temperature range of 573–623 K and the H2 pressure of 1.0–5.0 bar by high-resolution QENS. Unlike the Ru/MgO(110), the significantly higher H diffusive motions are clearly observed in the Ru/MgO(111) within the instrument time window. QENS data analysis reveals that this diffusion follows the H+ hopping mechanism by which the H+ migrates over the surface oxides (O2−) of the polar MgO(111), with the jump distance (R) of ≈2.90–2.98 Å, nearly equivalent to the distance between oxide anion sites. A short characteristic residence time (τ) is calculated to be ≈8.86–15.26 ps. The results studied in current work strongly support our proposed fast H+ hopping mechanism and highlight the critical function of polar metal oxide support in promoting H mobility with a low degree of local covalency and hence contributing to excellent catalytic performance.
2 Results and Discussion
Dynamics of H species over the Ru/MgO(111) and Ru/MgO(110) surfaces was investigated using the QENS technique. QENS experiments were performed on the OSIRIS instrument via a high-flux backscattering, time-of-flight (TOF) spectrometer with an inverted geometry at the ISIS Pulsed Neutron and Muon Source, Rutherford Appleton Laboratory, allowing us to probe dynamics on the time scale of ≈1 to 65 ps.[8] In the QENS experiments, the recorded total scattering function S(Q, ω) consists of an elastic component occurring as a peak at energy transfer ℏω = 0 and a quasielastic component appearing as a broadening of the elastic peak. The elastic component represents immobile scattering species that can be modeled by a delta function convoluted with an instrument resolution function. On the other hand, the quasielastic component reflecting the moving species can involve one or more Lorentzian functions. As the incoherent scattering cross-section of H is significantly larger than all other elements, the observed broadening can be dominantly assigned to the uncorrelated motions of H atoms. Contribution of sample environments such as a coherent Bragg scattering from the Ru/MgO catalyst and the sample holder can be omitted by subtracting the QENS spectrum of the unloaded (postreduced) sample from that of the H2-loaded one (Figure S1, Supporting Information). Details of the QENS experiments and the surface characteristics of MgO are given in the Supporting Information and the recent work reported by Wu and coworkers,[2] respectively.
Figure 2a–d displays the temperature and pressure dependence of the quasielastic line shape at a momentum transfer (Q) of 0.89 Å−1, compared between the unloaded and H2-loaded samples. As can be seen, there is a substantial quasielastic broadening that changes with temperature and H2 pressure when measuring the Ru on polar MgO(111) sample (Figure 2a–c). This observation is in sharp contrast to the Ru on the conventional nonpolar MgO(110) sample where any H motion appeared to be miniscule within the spectroscopic window of the instrument, yielding little detectable broadening at all the measurement conditions (Figure 2d and Figure S2, Supporting Information). These results indicate that hydrogen motion is occurring on timescales visible to the OSIRIS spectrometer and that polar MgO(111) plays a key role in facilitating H mobility. For the Ru/MgO(110), we only performed data fitting analysis on the data acquired at 1.5 bar H2 and 573 K for comparison despite a high degree of error because the QENS signals at other conditions are also too low to provide significant quantitative fits.
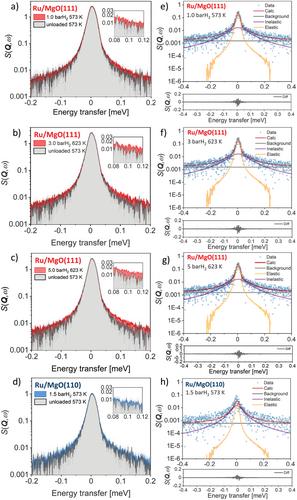
Data processing and fitting were carried out by using the Mantid data analysis suite developed at ISIS.[9, 10] Each of the subtracted QENS spectra was fitted with the model containing a delta function convoluted with the experimentally measured resolution function, a single Lorentzian function, and a flat background function. Further information on the QENS data analysis can be found in the Supporting Information. The convolution fits of the QENS spectra of Ru/MgO(111) at various temperatures and H2 pressures for Q = 0.89 Å−1 are presented in Figure 2e–g. The goodness of fit is determined by a chi-squared (χ2) test giving a value range of 0.70–0.74. It is worth noting that the data are fitted well with a delta function convoluted with the instrument resolution function, a flat background, and a single Lorentzian function, indicating one observable diffusive motion within the instrument window. The errors presented in the fitted spectra are computed based on least squares statistics.
It is challenging to relate the observable motion to specific H-containing species, such as H+, H−, or H2 on a particular substrate. We can clearly distinguish the diffusion of molecular and atomic hydrogen by considering the fact that H2 may exhibit both translational and rotational diffusion, which can be observed even at room temperature; whereas H+ and H− are expected to show mostly translational motion with only some limited degree of frustrated rotational modes.[5, 11-13] In this study, the broadening starts to be visible above 523 K and changes quantitatively at elevated temperature and pressure for Ru/MgO(111) and is nearly undetectable when using Ru/MgO(110). So, we can rule out the QENS signal from molecular H2 whose motions may not fit into the instrument time window. According to our previous analysis by nuclear magnetic resonance (NMR), Fourier transform infrared spectroscopy (FTIR), atmospheric pressure X-ray photoemission spectroscopy (AP-XPS), and density functional theory (DFT), the Ru/MgO(111) can be quickly covered with H, which is highly protonic in nature (as hydroxyl).[2, 3] As a consequence, we conclude that majority of the QENS signal is attributed to H+ diffusion.
The TW model, on the other hand, possesses discrete hops, where the jump lengths follow an exponential distribution with a diffusion coefficient D.
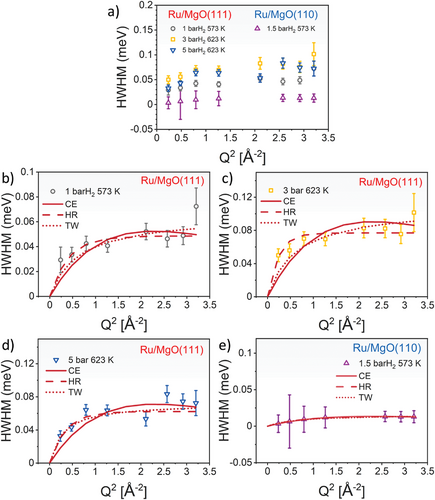
During data fitting for the Ru/MgO(111), the jump distance was initially restrained to 3.0 ± 0.4 Å to reflect the nearest-neighbouring O distances, including the hopping distance between two adjacent surface O2− sites according to the polar MgO(111) model (3.00 ± 0.03 Å). From Figure 3b–d and Table 1, all three models yield equally well fits to the observed data within error limit, making it less possible for us to explicitly choose one over the others to best describe the diffusion pathway. However, it is worth nothing that the correlation of the jump distance (R) and residence time (τ) with temperature and pressure is strongly consistent for the CE and HR models. The CE model apparently gives a better fit for a high Q (Q2 > 1.5 Å−2) region, whereas the HR model results in an inverse trend. The high Q data prominently depicts a short-range motion, making this observation sensible that there is a short-range order of O−O exists and becomes less pronounced in the long range. Under high temperature and pressure where surface reconstruction of MgO nanosheets enriched with Ru nanoparticles is possible, there is a possibility of distribution of the surface O−O distances responsible for the H+ jump rather than a fixed O−O distance demanded by CE model. Considering the whole Q range studied in this work, the HR model is slightly more suitable to best describe the observed H+ diffusion. The HR model provides average jump distances of 2.90–2.98 Å within experimental errors over the studied temperatures and H2 pressures. These results strongly demonstrate the existence of H+ hopping, constrained by the well-defined lattice O2− sites of the polar MgO(111) (Figure 1).
| Model | Temperature [K] | H2 pressure [bar] | Jump length R [Å] | Residence time τ [ps] | Reduced χ2 | D [10−5 cm2 s−1] | Eaa) [meV] | |
|---|---|---|---|---|---|---|---|---|
| Ru/MgO(111) | CE | 573 | 1.0 | 3.01 (0.20) | 15.26 (2.29) | 0.27 | 1.48 (0.45) | 333 (0.92) |
| CE | 623 | 3.0 | 3.00 (0.18) | 8.86 (1.21) | 0.53 | 2.54 (0.42) | ||
| CE | 623 | 5.0 | 2.96 (0.19) | 11.25 (1.70) | 0.52 | 1.94 (0.44) | ||
| HR | 573 | 1.0 | 2.98 (0.02) | 15.69 (0.94) | 0.19 | 1.41(0.25) | 341 (0.38) | |
| HR | 623 | 3.0 | 2.90 (0.75) | 8.55 (0.51) | 0.13 | 2.46 (0.72) | ||
| HR | 623 | 5.0 | 2.90 (0.97) | 11.02 (0.64) | 0.42 | 1.91 (0.82) | ||
| TW | 573 | 1.0 | 3.10 (1.06) | 10.11 (3.69) | 0.16 | 2.38 (0.88) | 315 (0.92) | |
| TW | 623 | 3.0 | 3.10 (0.81) | 6.05 (1.77) | 0.31 | 3.97 (0.77) | ||
| TW | 623 | 5.0 | 3.20 (1.14 | 10.25 (4.03) | 0.96 | 2.50 (0.90) | ||
| Ru/MgO(110) | CE | 573 | 1.5 | 3.00 (0.02) | 59.28 (0.84) | 0.04 | 0.38 (0.14) | NAb) |
| HR | 573 | 1.5 | 2.95 (1.76) | 56.92 (6.56) | 0.14 | 0.38 (1.09) | ||
| TW | 573 | 1.5 | 3.09 (0.49) | 40.97 (6.90) | 0.44 | 0.58 (0.60) |
- a) A rough activation energy, Ea is derived by using an Arrhenius law of the extracted mean residence time τ. Due to the measurement time constraint, data at two different temperatures (with a variation in pressure) were used in the estimation
- b) NA denotes as not applicable.
The τ values, which are in the range of 15.69 ± 0.94 – 8.55 ± 0.51 ps, decrease as a function of temperature but become longer as the H2 pressure rises (Table 1). The delay of τ with increasing H2 pressure could reflect slower mobility of H caused by higher surface coverage and hence reducing free space for the activated H+ to diffuse through. Full analysis of these pressure-dependent data may be possible with the aid of pressure-involved DFT calculations or molecular dynamics (MD) simulations, which will be reported in the near future.
Regarding the Ru/Mg(110), its HWHM profile can be best fitted with both the CE and HR models yielding an average jump length and a residence time of 3.00 ± 0.02 Å and 59.28 ± 0.84 ps for the CE model and 2.95± 1.76 Å and 56.92 ± 6.56 ps for the HR model, respectively, whereas the TW model gave marginally poorer fits (Figure 3e and Table 1). The obtained jump length is consistent with the distance of two adjacent surface O2−sites (2.98 ± 0.01 Å, see Figure 4), reflecting that similar H+ hopping exists in this material. The D value at 573 K and 1.5 bar H2 is calculated to be 0.38 ± 0.14 × 10−5 and 0.38 ± 1.09 × 10−5 cm2 s−1 for the CE and the HR models, respectively. Clearly, the Ru/Mg(110) gives a slower H+ diffusion rate compared to the polar Ru/MgO(111) counterpart, emphasizing a critical role of highly electrostatic oxide surface of MgO(111) in facilitating the H+ mobility.
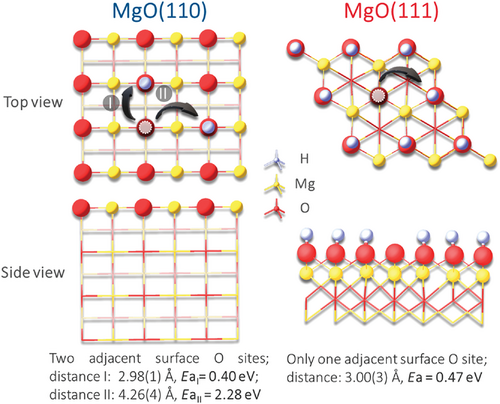
DFT calculations of the activation energies of H+ hopping over the MgO(110) and MgO(111) were carried out (Figure 4). The calculated hopping barriers of MgO(110) were found to depend critically on the distances of the adjacent O sites, namely the oxygen row with O–O distance of 2.98 ± 0.01 Å can give a lower hopping barrier of 0.40 eV but the longer distance of O–O of 4.26 ± 0.04 Å (interdispersed with Mg2+) gives a higher hopping barrier of 2.28 eV. Presumably, the closer distance in the former case allows H bonding between the oxygen sites during hopping as akin to the H+ conductivity by Grotthuss mechanism in water). However, the surface H migration at a long range could also be affected by geometric factors such as oxygen defect or cation interventions and electronic factor, i.e., local covalence to the hydrogenic species. In order to eliminate the effect of surface polarity of MgO(111) for comparison, a model of H+-saturated polar MgO(111) surface with only one H vacancy was used (increasing H+ coverage on MgO(111) facet was found to progressively reduce the surface polarity, see Figure S13 (Supporting Information), and FTIR and APXPS proved the high H+ coverage under experimental conditions as shown in Supporting Information[2]). Figure 4 shows that H+ hopping between the adjacent O sites with O–O distance of 3.00 ± 0.03 Å has a hopping barrier of 0.47 eV. This value is comparable to that of MgO(110) of one directional short O–O distance. Thus, the apparent higher H+ migration rate observed over MgO(111) than MgO(110) may reflect two contributions. First, the characteristic geometric factor where total oxygen terminated facet in polar MgO(111) enables H+ hopping in all different directions which is less disrupted by local interactions from oxygen defects/cations, in comparison to the MgO(110). Second and more importantly, the electronic factor of local surface polarity on H+ to give actually the lower experimental hopping barrier (∼0.3 eV) cannot be totally discounted.
As stated, significant research attention is being paid to the development of new H conducting solid-state materials for fuel cells, H storage materials, and related hydrogenation/dehydrogenation catalysis.[1, 2] Recently, there have been some significant advances in H+-conducting electrolytes, including polymers[18] and oxide ceramics.[19-21] In oxides, H usually incorporates as near proton character (Hδ+) that conduct by hopping from one lattice oxygen to another.[12, 13, 22] However, the covalency between Hδ+ and local lattice O2− offers a higher barrier for the diffusion. Hydride ion type (Hδ−) on oxide materials has also been considered for H conducting species, which shows a smaller degree of covalency but this time with neighboring cations, rather than simply occurring as a free H− ion.[4, 23, 24] While H+ ions are much smaller than H− ions, H− ions in oxide materials are often more mobile but the H− content is generally fairly low in oxide lattices. Their typical diffusion coefficients are higher for the oxide hydrides (≈6–10 × 10−5 cm2 s−1) than for typical H+ conductors (≈1–5 × 10−6 cm2 s−1) in the temperature range of ≈700–750 K, with the H+ conductor typically achieving similar diffusion coefficients in the range of 900–1000 K. So far, the research is to seek candidates with a compromise between hydride-like flow between sites that are partially covalently bonded to transition-metal cations, to proton-like move between sites attached to oxide anions to strike for high H conductivity. It is interesting to see that our obtained D values over Ru/MgO(111) exhibit at least one order of magnitude higher than most typical H+ conductors (1 × 10−6 cm2 s−1) at 700 K.[13, 25, 26] In addition, dimensionality of the diffusion pathways is equally important since it is inversely proportional to the D value as described in Equation (4). While H+ or H− travels in all three directions across the lattices of crystalline solid conductors, H migration over the energetically favourable O2− sites of the polar Ru/MgO(111) surfaces can yield a greater diffusion rate due to the diffusive directions being reduced to two. This surface H+ migration is strongly supported by an operando depth-profiling AP-XPS analysis, disclosing that H predominantly resides near the surface and travels horizontally across the oxygen surface.[2]
DFT calculations indicate that the H is indeed more protonic on MgO(111) than that of the nonpolar MgO(110).[2] Thus, the electrostatic polar MgO support at high H coverage clearly facilitates a more rapid protonic migration with lesser local covalence, reaching the same order of magnitude to LaSrCoO3H0.7 oxide hydride, as observed at 685 K.[27]
In addition, the activation energies derived from QENS data are similar to the oxide hydrides (≈200–230 meV) but significantly lower than typicalH+ conductors (≈400 meV). The above observations demonstrate that energetic interactions of the H+ dynamics in Ru/MgO(111) are in between those of H+-conducting oxide materials and oxyhydrides at high coverage of hydroxyl proton. Further exploring the use of polar oxide surfaces as media for H migration and reactions could be an interesting option in future.
3 Conclusion
In summary, H+ diffusion over the Ru-based MgO surfaces including Ru/MgO(111) and Ru/MgO(110) under H2 without moisture has been investigated by using an in situ QENS technique. Our QENS results indicate that the observable H+ hopping occurs across the surface oxides (O2−) of the MgO(111), with an average jump distance nearly equivalent to the distance between oxide anion sites. This degree of H+ mobility is drastically less detectable when using the Ru/MgO(110) material, suggesting a key role of polar metal oxide surface in facilitating the fast H+ transport. The H+ diffusion coefficients are in between 1.41 ± 0.25 and 2.46 ± 0.72 × 10−5 cm2 s−1 under the temperature of 573–623 K and the H2 pressure range of 1.0–5.0 bar. These values outperform those of H+-conducting oxides, reaching to a similar magnitude to oxyhydride materials. The calculated activation energy for this H+ hopping is ≈0.3 eV, also sensibly lower than H+-conducting oxides in which H+ is covalently bound to local O2− sites. We envisage that this finding of using polar oxide facets will provide insights into the rational design of efficient catalysts for H diffusion-involved reactions.
4 Experimental Section
Sample Preparation
The Ru/MgO(111) and Ru/MgO(110) materials investigated in the current study were prepared by following the procedure previously reported by the group.[2, 3] Since these samples were taken from the same batch, the comprehensive characterization of these materials can be found in the aforementioned paper.
QENS Experiments
QENS experiments were performed on the OSIRIS instrument, a high-flux backscattering, TOF spectrometer with an inverted geometry at the ISIS Pulsed Neutron and Muon Source, Rutherford Appleton Laboratory.[8] QENS technique was used to study the H mobility on the Ru-based MgO catalyst surface, as a function of temperature and H2 pressure. A polychromatic beam of neutrons first illuminated the sample. After scattering, the neutrons were Bragg reflected by the pyrolytic graphite 002 crystal analyzer to define a single final energy (1.845 meV). The scattered neutrons with fixed energy then travelled toward the 42-element 3He detectors. The scattered neutrons were detected over an angular range of 2θ = 11°–155°. The instrumental resolution and detector efficiencies were calibrated by fitting the spectrum of a vanadium standard. The elastic energy resolution was 24.5 µeV. The energy transfer (ΔE) range was ±0.4 meV and the momentum transfer (Q) range was 0.18–1.8 Å−1. Details of the QENS experiments as well as DFT calculations are given in the Supporting Information.
Acknowledgements
T.Y. and J.M. contributed equally to this work. ISIS Neutron and Muon Source (UK) is gratefully thanked for providing the QENS facility on the OSIRIS beamline (RB2010394). Gemma Draper, Adam Sears, and Paul Macintyre are sincerely appreciated for their technical help in gas handling and furnace. This project was financially supported by the National Natural Science Foundation of China (22003016 and 92145302).
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available in the supplementary material of this article.