Freshwater essential for civilization faces risk from untreated effluents discharged by industries, agriculture, urban areas, and other sources. Increasing demand and abstraction of freshwater deteriorate the pollution scenario more. Hence, water quality analysis (WQA) is an important task for researchers and policymakers to maintain sustainability and public health. This study aims to gather and discuss the methods used for WQA by the researchers, focusing on their advantages and limitations. Simultaneously, this study compares different WQA methods, discussing their trends and future directions. Publications from the past decade on WQA are reviewed, and insights are explored to aggregate them in particular categories. Three major approaches, namely—water quality indexing, water quality modeling (WQM) and artificial intelligence-based WQM, are recognized. Different methodologies adopted to execute these three approaches are presented in this study, which leads to formulate a comparative discussion. Using statistical operations and soft computing techniques have been done by researchers to combat the subjectivity error in indexing. To achieve better results, WQMs are being modified to incorporate the physical processes influencing water quality more robustly. The utilization of artificial intelligence was primarily restricted to conventional networks, but in the last 5 years, implications of deep learning have increased rapidly and exhibited good results with the hybridization of feature extracting and time series modeling. Overall, this study is a valuable resource for researchers dedicated to WQA.

1 INTRODUCTION

A river flows due to gravity, carrying water from precipitation, snowmelt, and partial aquifer storage as base flow towards the ocean or larger river as a tributary. Rivers have been vital for civilizations, providing water and major transport routes while supporting diverse ecosystems (Giri, 2021). Globally, river water is used for drinking, domestic, industrial, and agricultural purposes. The Earth's water reserve is mainly in oceans with ~96% as saltwater, only 1.1% being freshwater. Aquifers hold 99% of freshwater while rivers comprise just 0.0001% of total water reserves. Rivers, despite their low percentage, are crucial in human life and have been extensively studied in fields like hydrology, hydraulics, ecology, environment etc. (Syeed et al., 2023).

The population boom has increased water demand, putting pressure on all freshwater sources, including rivers. Anthropogenic influence quickened river pollution by affecting river water in two ways. Firstly, the over-extraction of water raised pollutant levels, and secondly, the anthropogenic activities add pollutants to water (Schwarzenbach et al., 2010). Industries in river catchments discharge harmful pollutants that contaminate the river. Agricultural runoff carries contaminants that negatively impact rivers. Domestic sources also contribute to river pollution. These combined effects have sparked global research interest in tackling river water quality (WQ) and pollution issues. Various researchers worldwide have aimed to identify pollutant sources, assess impacts, select key parameters, zone river pollution, predict and monitor river WQ, explore relationships between WQ and river conditions, and evaluate the ecological impact of river WQ (Schaffner et al., 2009). Significant literatures exist on assessing, monitoring, and modeling river WQ and pollution using diverse methods to address the challenge, with many researchers summarizing these efforts. Existing assessment techniques are improving with new modeling, data collection, and increased computational power. New methods are emerging, performing satisfactorily, and often outperforming traditional methods. Researchers are reviewing studies to explore the various methods used globally for WQA and modeling.

Gupta and Gupta (2021) reviewed papers published during 2010–2021 on water quality indexing (WQI) to assess river water status. The number of papers in SCOPUS and SCIE journals increased from around 750 to 2500 during this period. The WQI forms through four steps: selecting quality parameters, scaling them uniformly, assigning weights, and defining an aggregation function for the final result. These four steps can be executed in different manners (Sutadian et al., 2016). The selection of parameters is subdivided into three groups based on the number of parameters used: fixed, open, and mixed systems. Parameter selection involves reviewing literatures, data availability, parameter redundancy, and intended water use. In indexing systems, parameters are selected using expert judgment or statistical methods like principal component analysis (PCA) or correlation studies. The sub-indexing step can be divided into experts' opinions, standard WQ values, and statistical methods.

Delphi method, analytical hierarchy process (AHP), budget allocation procedure, and revised Simo's procedure are used in WQI models to determine parameter weights. In most WQI models, aggregation functions are created using additive or multiplicative functions. Researchers use modified functions and a combination of additive and geometric methods to address issues with raising eclipsing and uncertainty concerns. Gupta and Gupta (2021) classified the WQI into four groups: general, specific, designing/planning, and statistical indices. First one ignores the purpose of water utilization, while the second one specifies the quality level for a particular use. Third one formulates system design or planning, while the last relies solely on statistical methods.

The forms and formula of WQI have evolved since Horton (1965) first developed it. Total 13 indices such as National Sanitation Foundation WQI (NSFWQI) in 1970, Prati's index of pollution (IP) in 1971, McDuffie's river pollution index (McDuffie's RPI) in 1973, Bhargava's WQI (BWQI) in 1983, Oregon WQI (OWQI) developed in an updated form in 1995 after its first formation in late 1970s, Dinius WQI (DWQI) in 1987, Ved Prakash WQI (VWQI) in 1990, Aquatic toxicity index (ATI) in 1992, British Columbia WQI (BCWQI) in 1995, Canadian council of ministers of the environment WQI (CCMEWQI) in 1999, Overall index of pollution (OIP) in 2003, Universal WQI (UWQI) in 2007 and weighted arithmetic WQI (WAWQI) in 2011, represent the evolution of WQIs. Applying these indices is crucial for WQ research as they simplify the status for public understanding. The spatiotemporal extent of rigorously formulating WQ has sparked controversy among researchers, which is seen as a major limitation of the indexing method.

Uddin et al. (2021) outlined key issues in applying WQI. The model eclipsing problem arises from the aggregate function's nature used to calculate the final index score in many cases. By adjusting the sub-index ratings for dissolved oxygen (DO) and faecal coliform, the final index score changes concavely and linearly with a large interception for additive and multiplicative aggregation functions respectively. WQ may appear acceptable based on the final index score, despite individual parameters exceeding permissible limits. The minimum operator function has been used to address this issue. Uncertainty in WQI models arises from parameter selection, sub-indexing and weighting, contributing to inherent issues. Selection of WQ parameters (WQPs) is a key consideration in developing WQIs. Different WQI models have varying parameter numbers, from under five to around 30. The data availability is a concern for modelers using a specific WQI form. The parameters are commonly chosen based on expert opinion. Subjectivity error often arises in indexing. Statistical methods like Spearman's rank correlation coefficient, and PCA are used to exclude highly correlated parameters. In the mathematical part, there are issues with calculating sub-index values, parameter weighting and evaluating the aggregation function. These issues include confining parameter importance, subjectivity errors and issues of uncertainty and eclipsing.

Other than WQI, water quality modeling (WQM) involves mathematically simulating WQPs under certain pollutant loads, hydraulic scenarios and hydrological scenarios. WQM simplifies physical reality by focusing on a single or a few governing processes. Wang et al. (2013) outlined the historical evolution of WQM stages, categorizing them into primary (1925–1965), improving (1965–1995), and deepening (post-1995) stages. At first, bilinear BOD-DO models assumed industrial point loads as the primary factor influencing this relationship. External outputs like hydrodynamic factors, oxygen demand for sediment, and algal colonies were considered. The BOD was classified as carbonized and nitrifying, with added complexity from the concept of BOD reduction through sediment depositions. During the improvement stage, the models assessed six linear systems for predicting WQPs before moving to nonlinear systems development. The model development stage incorporated P and N cycles, nutrient-growth rate relationship, the use of finite difference method for solving nonlinear equations, hydrodynamic conditions, and sediment influences. During the deepening stage, air quality models were integrated into WQM to address atmospheric deposition considering tidal effects.

Sharma and Kansal (2013) categorized WQMs into simulation and optimization models. These two groups were further classified into physical and mathematical simulation models, and into linear, nonlinear, and dynamic optimization models. The mathematical models are subdivided into groups based on the assumed process, data type, solution type and geographic scale. The review included six models with their equations, application domains, and limitations. Gao and Li (2014) reviewed eight WQMs, discussing artificial intelligence (AI), integrating models and using remote sensing/GIS for large-scale spatial data, highlighting benefits, drawbacks, and future perspectives. Burigato Costa et al. (2019) found that SWAT (soil and water assessment tool) followed by QUAL models are widely used worldwide. Issues arise with non-standardized WQMs when applied outside their original conditions, leading to simulation errors. In these reviews, a key error in WQMs is using geography-specific rate constants, restricting its wide geographic application. To address this, many suggested calibration and uncertainty analysis.

AI models integrated into WQM offer various overviews (Tiyasha et al., 2020). The importance of AI models is clear because WQ data is complex, nonlinear, nonstationary, and connected to various factors. These AI models can be classified into five main groups: Artificial Neural Network (ANN), fuzzy logic-based, kernel-based, hybrid and complementary. The application of AI in WQM involves using various quality parameters as input to predict one or more output parameters. Different literatures consider the temporal resolution at daily, weekly, or monthly intervals. Hybrid and complimentary models generally outperform others, despite the advantages and disadvantages of individual models.

Rajaee et al. (2020) reviewed 51 literatures published during 2000–2016 regarding the use of AI models in WQM. DO and suspended sediment load are the most predicted variables globally using AI models. Daily and monthly predictions are common in literature, showcasing hybrid models' superiority over single-structure models. Ighalo et al. (2021) found that the most popular AI models during 2010–2020 were Adaptive Neuro Fuzzy Inference System (ANFIS), followed by ANN. Wavelet-ANN, wavelet-ANFIS, and ANFIS were successful in predicting the WQPs, with BOD being the most frequently used parameter in literatures.

Previous review studies reveal three major strategies used globally in WQ analysis (Figure 1): WQI utilization, mathematical modeling, and data-driven AI-based modeling. Previous reviews of WQM strategies mostly focused on certain sectors, leaving other sectors unexplored within a single study.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Major and sub-approaches preferred for water quality analysis.

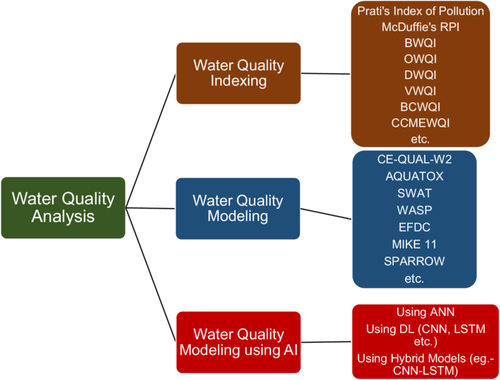
This study aims to achieve three main objectives: (i) present and summarize all the major approaches the scientific community adopts in WQ analysis, (ii) comparatively discuss three modeling strategies to find out the overall and strategy-specific gaps and outline application domains for each approach, (iii) profile the future directions for each strategy to make the step forward more robust and comprehensive. The novelty of this study is to present the latest developments in WQ analysis approaches and facilitates a comparative discussion among these approaches to benefit the research community.

2 WQA APPROACHES

2.1 WQI development

WQI is a well-researched topic worldwide in WQA. Due to the complex relationships among various parameters and the influence of the environment, conveying WQ accurately with numerical values is difficult. Horton (1965) pioneered the concept of WQI to simplify this by providing a single score. Since then, the scientific community has continued to develop and address various issues related to WQA.

The development of WQI involves four key steps: parameter selection, sub-index generation, weight assignment, and aggregation function design (Figure 2). These steps produce a value that indicates the WQ level. Subsequent sections detail researchers' methods, advantages, and limitations in carrying out these steps for WQI calculation.

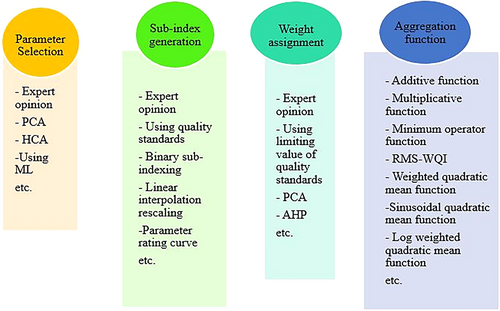
2.1.1 Parameter selection

Parameter selection in WQI development is highly subjective, influenced by varying geography leading to a lack of standardized parameter sets. Brown et al. (1970) used the Delphi method to involve experts in creating a comprehensive parameter list. Subsequently, various literatures also gathered expert opinions to compile parameter lists (Bordalo et al., 2006; Dojlido et al., 1994; Liou et al., 2004; Stambuk-Giljanovic, 1999; Swaroop Bhargava, 1983). In the past decade, PCA has been successfully used to generate multiple PCs with different loadings for each parameter. The significant components explain the majority of the data set's variance and are consequently chosen for developing WQI parameters (Dutta et al., 2018; Fathi et al., 2018; Tripathi & Singal, 2019; Ustaoğlu et al., 2020; Zeinalzadeh & Rezaei, 2017). Other statistical techniques provide valuable insights into WQP selection. Correlation study (Aydin et al., 2021; Shil et al., 2019) and hierarchical cluster analysis (Arora & Keshari, 2021; Njuguna et al., 2020) among different WQPs exhibit important relationships among them and help to make decisions about the parameter selection. A comprehensive literature survey is a useful method to achieve this objective where published literatures explain the significance of selected WQPs (Gani et al., 2023; Mishra et al., 2024). A multi-stepped technique was adopted to select the WQPs for developing West-Java WQI (WJWQI). Two screening procedures with reference to data availability followed by correlation studies to identify parameters expressing the same and omitting was done to reduce the dimensionality (Sutadian et al., 2018). Various studies select parameters focusing on specific water use sectors, with differences seen in the literature. Shil et al. (2019) assessed the WQI for irrigation water. The WQPs considered following FAO guidelines, which were sodium adsorption ratio, residual sodium carbonate, residual sodium bicarbonate, magnesium hazard, potential salinity, pH, chloride, electrical conductivity, and total dissolved solids (TDS). Multiple combinations of input parameters were used for WQI development using machine learning (ML) models. The combination produced the best values of performance indicators and was selected (Sakaa et al., 2022). This method is feasible only with the use of ML models for WQI development.

2.1.2 Sub-index generation

The WQPs are expressed in different units covering different ranges, preventing direct use of raw numerical values in WQI development. The parameter values are unified into a single scale called sub-index, simplifying the overall representation. Different methods of evaluating the sub-index have evolved with new WQI formations. Expert opinion is the primary method for sub-index evaluations. Horton (1965) and Brown et al. (1970) scaled parameters on a 0–100 scale based on their impacts on WQ. Pesce, (2000) provided a table of normalization factors for deriving sub-index values used in several studies (Koçer & Sevgili, 2014; Misaghi et al., 2017; Wu et al., 2021). House (1989) demonstrated using WQ standards to calculate sub-index values. Many studies used both standard and measured parameter values to calculate the sub-index (Ewaid & Abed, 2017; Goher et al., 2014; Oni & Fasakin, 2016; Sahoo et al., 2015; Tiwari et al., 2015).

The standard and ideal values are set based on local regulatory authorities, WHO, and FAO. Equations (1) and (2) present the mathematical formulation. Researchers often apply a binary sub-indexing system, using values of 0 and 100. A value within the permissible limit corresponds to a sub-index of 0, otherwise, it is 100 (Parween et al., 2022; Gani et al., 2023). Mishra et al. (2024) used a natural break algorithm on the measured data range to derive sub-index values.

Q_{i} = \frac{V_{i} - V_{0}}{S_{i} - V_{0}},

()

Q_{i} = 100 \times \frac{V_{i}}{S_{i}} .

()

Linear interpolation rescaling (Equations (3) and (4)) was conducted by Sutadian et al. (2018) and Ding et al. (2023). Shah and Joshi (2017) took the deviation from the maximum contamination level to derive sub-index. Sharma and Reddy (2013) prepared parameter rating curves to convert parameter values into sub-index values according to Indian effluent standards and literatures. These rating curves are used to derive sub-index values (Tiwari et al., 2018).

Q_{i} = C_{1} - (C_{1} - C_{2}) (\frac{V_{i} - V_{1}}{V_{2} - V_{1}}),

()

Q_{i} = C_{1} - (C_{1} - C_{2}) (\frac{V_{1} - V_{i}}{V_{1} - V_{2}}),

()

where Q_i represents sub-index value for ith parameter, V_i is measured value, S_i is standard permissible value, V₀ is ideal value, C₁ and C₂ are upper and lower class limits, and V₁ and V₂ are upper and lower allowed values for WQPs.

2.1.3 Calculation of weights

Weights are assigned to each WQP based on their relative importance in developing the WQI. When the WQI aggregation function is additive, it is compared with variable coefficients mathematically. Researchers provide this weight according to expert opinion. Some traditional WQI models (Horton's index, NSFWQI, CCMEWQI, Prati's index etc.) assign weights based on expert knowledge, leading to subjective errors and lacking reflection of geographical and environmental variations. Equal weights are used for some WQI models across all parameters (Cude, 2001; Dojlido et al., 1994; Thi Minh Hanh et al., 2011; Prati & Richardson, 1971; Wepener et al., 1992). The equal weighting of parameters in WQI does not eliminate subjectivity error as relative importance can differ under certain scenarios. To address this, many researchers explored the assumption that weight is inversely related to the standard limits of WQPs (Dutta et al., 2018; Ewaid & Abed, 2017; Goher et al., 2014; Kadam et al., 2019; Lkr et al., 2020). Equations (5a) and (5b) outline weight calculations in this objective method. While it minimizes subjectivity error, it is detached from the physical process of pollution, so parameters under limits can still affect pollution significantly. Even if the TSS of a river is below the limit, it can still impact pollution through the sorption of nutrients and pollutants.

W_{i} = K / S_{i},

()

K = \frac{1}{\sum_{i = 1}^{n} (1 / S_{i})},

()

where, W_i is weight assigned, S_i is recommended permissible value for n number of parameters, and K is proportionality constant.

Many have adopted the AHP method of multi-criteria decision-making to calculate weights (Mishra et al., 2024; Rajkumar et al., 2022; Sutadian et al., 2018). In this method, a consistency ratio is checked and has to be minimized under a threshold value to determine the WQP weights. Due to AHP's high uncertainty and lack of straightforward methods to manage it, researchers have turned to entropy-based approaches for calculating these weights (Niknam et al., 2024; Verma et al., 2022). A lower parameter entropy implies greater system influence and warrants a higher weight assignment. Equations (6a) and (6b) represent entropy and weight.

P_{i j} = \frac{y_{i j}}{\sum_{i = 1}^{m} y_{i j}},

()

e_{j} = - K \sum_{i = 1}^{m} P_{i j} \ln P_{i j},

()

where, P_ij represents parameter index amount, y_ij is normalized value of jth parameter for ith sample, e_j signifies the entropy, K = 1/ln(m) and m is sample count.

Several researchers use PCA for weight calculation, finding it a rational method (Naik et al., 2022; Roy et al., 2024; Sabinaya et al., 2024). The equation of the derived principal components gives the weight directly. PCA offers the crucial parameters and weights in one analysis. In contrast, Ding et al. (2023) blended subjective and objective weights using game theory to determine the final weight for each parameter.

2.1.4 Aggregation function

During the aggregation stage in WQI development, weighted index values are mathematically combined to derive the final quality score. In earlier stages, both additive and multiplicative aggregation functions are commonly used in several well-known WQI models. Equations (7a) and (7b) show the generic form of these functions.

W Q I = \sum_{i = 1}^{n} s_{i} W_{i},

()

W Q I = \prod_{i = 1}^{n} {s_{i}}^{W_{i}},

()

where, s stands for sub-index value.

Though Ott (1978) used “eclipsing” for errors from additive or multiplicative factors, which can arise during parameter weighting and sub-indexing processes. The issue occurs when some parameters exceed limits but are balanced by better conditions in other areas, resulting in a seemingly good overall WQ score. For example, if parameters A, B, and C are weighted equally at 0.33 and have sub-index values of 20, 30, and 90, the additive aggregation yields a good final quality score of 46.2. However, parameter C has exceeded its permissible limit, posing serious adverse effects on WQ which is being suppressed in the aggregated result.

Smith (1990) suggested using the minimum operator function to avoid the eclipsing problem. The minimum operator function calculates the final score using the sub-index value of the worst-conditioned parameter. However, it underuses available information on WQ and hence reduces efficiency. Few other formulated aggregation functions are the square root of harmonic mean (Gazzaz et al., 2015), non-equal weighted geometric method (Sutadian et al., 2018), RMS-WQI (Gani et al., 2023), weighted, log-weighted and sinusoidal quadratic mean function (Ding et al., 2023).

The mentioned four steps are core in many WQI models. Yet, some models deviate from performance. Here, we briefly explore two such models: fuzzy inference system (FIS) and CCMEWQI.

2.1.5 Fuzzy inference system

The FIS mainly includes membership functions, fuzzy set operations, fuzzy logic, inference rules and defuzzification process to determine the final quality score (Zadeh, 1965). The common membership functions used are trapezoidal and triangular in shape. These functions normalize the quality parameter values during set operations. The fuzzy logic mainly consists of If–then statements, conceived from expert knowledge in many cases. Centroid method is commonly used for defuzzification to get the final WQI value. Researchers use FIS mostly in the inference part, which parallels the four steps of WQI development (Uddin et al., 2021). Tiwari et al. (2018) used subtractive clustering and fuzzy c-means clustering adaptive neuro-fuzzy inference system (ANFIS) with expert opinions' weights and sub-indexes from transformation equations to achieve the final outcome. Sahoo et al. (2015) used PCA to reduce parameters and their weights before feeding the PCA-processed data into ANFIS network. Mourhir et al. (2014) used the minimum operator function on two WQIs to get the worst conditioned parameters and their weight. These two WQI models evaluated fuzzy membership function ranges and performed defuzzification using the centroid method.

2.1.6 CCMEWQI

The CCMEWQI (CCME, 2001; Nazeer et al., 2014) is such a model that does not require parameter sub-index calculation and evaluation of weights. This index needs at least four variables. The aggregation function is formulated by parameters F₁, F₂, and F₃ representing scope, frequency, and amplitude. F₁ exhibits the ratio of several variables which do not meet the objective at least once in the total study period and the total number of variables. F₂ is analogous to F₁, but with variables replaced by tests, and F3 measures the extent to which failed variables deviate from desired values. The CCMEWQI used worldwide to assess WQ, is theoretically defined by Equations (8a)–(8e).

WQI = 100 - [\frac{\sqrt{{F_{1}}^{2} + {F_{2}}^{2} + {F_{3}}^{2}}}{1.732}],

()

F_{1} = \frac{Number of variables not meeting the objective}{Total number of variables} \times 100,

()

F_{2} = \frac{Numberof tests not meeting the objective}{Total number of variables} \times 100,

()

F_{3} = \frac{n s e}{0.01 n s e + 0.01},

()

n s e = \frac{\sum_{i = 1}^{n} departure}{number of tests},

()

where nse is the normalized sum of excursions of the parameter values.

2.1.7 Limitations

Despite its simple model structure and benefits of depicting results spatially and numerically with minimal data, the WQI approach has significant limitations that require attention for future improvements. The framework for WQI development lacks a universally validated form. Parameters, sub-indexing, weights, and aggregation methods vary across locations due to environmental factors and prior local knowledge. Reducing generalizability and increasing subjectivity errors are consequences of this limitation in the model. Uncertainty in WQI models can arise in all four development steps, posing another issue. The impact of a contaminant on WQ status may vary by geography during parameter selection. The WQI framework does not consider this variation, causing uncertainty in the model. Weight assignment in WQI development is subjective and a significant source of uncertainty. In sub-index generation, the mathematical formulation (Equations (1)–(4)) adds uncertainty. When aggregating the function, ambiguity and eclipsing scenarios may arise. If the aggregated WQ appears worse than individual parameter sub-index values, it is termed ambiguity. The opposite, called eclipsing, occurs when individual values are poor but the overall index suggests otherwise. Both ambiguity and eclipsing increase model uncertainty (Syeed et al., 2023). Uncertainty levels vary with the standards for WQ classification. Seifi et al. (2020) found that incorporating BIS standards led to the least uncertainty in parameter weight assignments when developing WQI. Many studies estimated uncertainty and created frameworks to reduce it (Pak et al., 2021; Uddin, Nash, et al., 2023). Sensitivity analysis helps select parameters accurately, reducing uncertainties in the parameter selection step. The basic way to assess sensitivity is by removing a parameter and observing its impact on the result. Talukdar et al. (2024) tested the WQI of a lake and found that removing TDS and EC from the analysis could enhance result accuracy by reducing uncertainty. The study recommended closer monitoring of pH and turbidity due to their significant impact on WQ. Therefore, sensitivity analysis identifies unimportant or uncertain parameters, as well as crucial ones for determining WQ status. Sensitivity analysis methods for WQI models expand with the application of statistical, probabilistic, and ML techniques. Therefore, conducting uncertainty and sensitivity analysis in WQI modeling is crucial for making more reliable conclusions.

2.2 Water quality modeling

The WQ reflects the overall water condition, which is the result of interactions between biotic and abiotic constituents. Modeling these processes is complex due to many interrelationships and physical phenomena. Each WQM is defined by its conceptualization, simulated processes, required input data, strengths, limitations, and application domain. The pollutant concentration in rivers is linked to hydrodynamic, hydrologic, and ecological factors, making comprehensive WQM challenging, with model performance sensitive to environmental conditions. Previous reviews have described specific WQMs and their specifications mentioned in the introduction section. Various model components are highlighted here to discuss evolution and predict future trends.

2.2.1 Historical development of conceptualization of WQM

In the Streeter and Phelps (1925) model, DO and BOD are linearly related as the basic form of WQM. The study focused on stream point loads to predict DO patterns using a sag curve for longitudinal profiles. Oxygen depletion depends on microorganisms using DO to digest organic matter of water, linked to both microbe count and atmospheric reaeration. After developing this basic framework, various researchers added other factors and processes to express reality holistically. Thomas (1949) included sediment deposition and flocculation in studying DO and BOD dynamics. Dobbins (1964) added algal photosynthesis and respiration factors affecting DO levels, emphasizing shifts in BOD due to sediment release. Only advection was considered in these developments, leading to the execution of one-dimensional models. The initial step in WQM involves modeling the dispersion process to enhance the result dimensionality and predictive capabilities of the model. The quality parameters were predicted as a function of time and space. So, more advanced numerical techniques were used to solve the process equations of WQMs (Gough, 1969; Welander, 1968). Other processes were also started alongside these changes. The N and P cycles, biotic responses, sediment hydraulics, and hydrological integration were incorporated into WQMs to enhance performance (Riffat, 2012; Yih & Davidson, 1975). Recent complex additions to WQMs involve integrating air quality models to assess atmospheric depositions in waterbodies (Golomb et al., 1997; Morselli et al., 2003; Poor et al., 2001). Figure 3 illustrates the key features of each step of the historical development of WQM.

This study reviews seven popular WQMs, summarizing their development and research applications over the last decade. The reviewed models are CE-QUAL-W2, AQUATOX, SWAT, WASP and environmental fluid dynamics code (EFDC).

2.2.2 CE-QUAL-W2

This two-dimensional model was developed by the US Army Corps Engineers, simulating hydrodynamic and WQ properties while averaging such properties. Longitudinal and vertical profiles of output parameters were evaluated, which were most successfully applicable to narrow waterbodies with considerable length and depth. In 1975, CE-QUAL-W2, previously known as laterally averaged reservoir model, was initially developed for reservoir modeling. After that, the generalized longitudinal-vertical hydrodynamics and transport model was developed with enhancements to the original model. In 1986, CE-QUAL-W2 was again upgraded by integrating the WQM (Cole & Wells, 2006). This model solves the momentum equation in the longitudinal and vertical directions, assuming hydrostatic pressure distribution. Equations (9) and (10) show the governing equations for the hydrodynamic simulation model.

\begin{array}{l} \frac{\partial U B}{\partial t} + \frac{\partial (U U B)}{\partial x} + \frac{\partial (W U B)}{\partial z} \\ = g B \sin β - \frac{B}{ρ} \frac{\partial P}{\partial x} + \frac{1}{P} \frac{\partial B τ_{x x}}{\partial x} + \frac{1}{ρ} \frac{\partial B τ_{x z}}{\partial z}, \end{array}

()

\frac{1}{ρ} \frac{\partial P}{\partial z} = g \cos β,

()

where U and W denote velocity in x and z directions, B represents waterbody width, P stands for the hydrostatic pressure, ρ is density, τ_xx and τ_xz are shear stresses acting longitudinally, g is gravity acceleration, and β is longitudinal bed slope.

The WQM is done by evaluating 46 WQPs as state variables and more than 60 derived variables covering physical, chemical and biological types. The oxygen profile, constituent concentration profile, eutrophication, and bacteriological quantities are simulated in every grid and time step (Bai et al., 2022). In the past decade, researchers primarily used the CE-QUAL-W2 model in reservoirs and rivers to simulate WQ profiles. Modifications and additional processes were made for simulating WQPs. For example, Zhang et al. (2015) improved a model by adding a sediment diagenesis module to improve sediment oxygen demand (SOD) evaluation. The module considered carbon, nitrogen, and phosphorus cycles through 22 state variables, computing SOD as the sum of nitrogen, methane, and hydrogen sulfide SODs. Tested at the lower Minnesota River, the model showed satisfactory performance in predicting ammonia, nitrate, phosphate, and DO concentrations. Afshar et al. (2017) replaced conservative mass transport with volatilization for predicting the fate of volatile organic compounds. Their model also considers degradation, settling, and biological processes. The new module was calibrated by adjusting viscosity and diffusivity parameters. Shoaei et al. (2022) developed a modified heavy metal module for lead (Pb) in water, focusing on its transportation and transformation. The heavy metal phases included particulate and dissolved forms, changing through desorption and sorption processes. Adsorption and desorption rates depend on total metal concentrations and reaction rates. This study evaluated the reaction rate of Pb based on temperature, DO, TDS, and suspended solids. Genetic algorithm (GA) was used to optimize the reaction rate with the best results obtained using all parameters.

2.2.3 AQUATOX

AQUATOX is a simulation model that assesses pollutant fate and its impact on aquatic life and ecosystems. It uniquely evaluates risk factors for aquatic life from water pollution patterns. The model comprehensively represents stratified and well-mixed systems in various waterbodies like ponds, lakes, and streams. AQUATOX models biotic elements of water bodies like algae, macrophytes, and animals, representing biomass with ash-free dry weight and chlorophyll quantities (Moses et al., 2015). The AQUATOX model now includes sediment diagenesis in remineralization processes. The detritus, including nonliving organic materials and decomposers, splits into refractory and labile materials, with sub-categories like dissolved, suspended, deposited and buried. The DO is modeled as a function of reaeration, photosynthesis of aquatic plants, respiration of all living bodies, decomposition of organic materials and nitrification process. The system also models inorganic carbon, pH, calcium carbonate, phosphorus and nitrogen and the effect of toxic organic chemicals. Equations (11) and (12) describe the movement of state variables in AQUATOX (Park et al., 2008).

{Wash}_{in} = \sum_{upstream links} \frac{{Washout}_{us} \times {Vol}_{us} \times {FracWash}_{ThisLink}}{{Vol}_{ds}},

()

{Washin}_{ToxCarrier} = \sum_{upstreamlinks} \frac{{Washout}_{Carrier} \times {PPB}_{Carrier} \times {Vol}_{us} \times {FracWash}_{ThisLink}}{{Vol}_{ds}},

()

where, Wash_in = inflow load from upstream segment; Washout_us = washout from the upstream segment, Volume_Segment = volume of given segment; FracWash_ThisLink = fraction of upstream segment's outflow that goes to this particular downstream segment; Washin_ToxCarrier = inflow load of toxicant sorbed to a carrier from an upstream segment; Washout_Carrier = washout of toxicant carrier from upstream; PPB_Carrier = concentration of toxicant in carrier upstream.

Over the last decade, the AQUATOX model has been applied in WQM to assess how WQ affects ecological health. Case studies also explored hypothetical scenarios to devise improvement strategies. Akkoyunlu and Karaaslan (2015) applied AQUATOX in Mogan Lake to evaluate how a virtual wetland could enhance the trophic state. They projected a transition from hypertrophic to eutrophic, followed by a shift to a mesotrophic condition. The AQUATOX model integrated with WASP and SWAT predicts nutrient concentrations and WQ by adjusting the point and non-point source loadings (Elçi et al., 2018). Several studies examined the impact of some particular contaminants on waterbody health and ecological status. Lombardo et al. (2015) executed the risk assessment of Tricoslan and Alkylbenzene Sulfonate on the food web of a river ecosystem. The impact of polycyclic aromatic hydrocarbons on eutrophicated lake systems in China was studied using AQUATOX. Both the direct toxic impact and indirect ecological impact were assessed (Zhang et al., 2018). Ma et al. (2024) evaluated the potential risk of per-polyfluoroalkyl substances in aquatic ecosystems.

2.2.4 SWAT

SWAT is a physical-based, semi-distributed watershed model that simulates WQs in a continuous time scale in single or multiple sub-basins. Sub-basins are further divided into hydrological response units. This model evaluates nutrient generation with spatial and temporal variations (Arnold et al., 2012). SWAT needs topographical, soil, land-use land-cover and climatic data to simulate hydrological and WQ scenarios. Agricultural management practices in SWAT can model nutrient generation, nitrogen, phosphorus, pesticides, bacteria and carbon cycle in soil and its transportation. The algae growth, carbonaceous biological oxygen demand (CBOD), and DO are quantified as WQPs alongwith nutrient and pesticide concentrations. The exchange of pesticides between water column and sediment is done through solid-liquid partitioning, degradation, resuspension, diffusion and burial processes. SWAT model incorporates modules for bacteria and heavy metal routings (Arnold et al., 1998). The governing equation of SWAT is given in Equation (13).

S W_{t} = S W_{0} + \sum_{i = 1}^{t} (R_{day} - Q_{surf} - E_{a} - W_{seep} - Q_{g w}),

()

where SW_t is the soil water content at time t with SW₀ as initial moisture content, R_day as daily rainfall, Q_surf as surface runoff, E_a as evapotranspiration, W_seep as water content transmitted down to vadose zone, and Q_gw as base flow.

Over the past decade, the scientific community has extensively utilized SWAT for multiple purposes: estimating nutrient levels, analyzing the influence of land use on WQ, combining SWAT with machine learning, enhancing SWAT predictions through source code modifications, and pinpointing critical zones. Abbaspour et al. (2015) estimated nitrogen concentration in 14 Europe basins using catchment data, showing R² range of 0.28–0.65 during the calibration period. Epelde et al. (2015) assessed the nitrogen budget in the Alegria River outlet and showed a surplus of 114 and 65 kg.N.ha⁻¹.year⁻¹ through two decades from 1990 to 2011. The nitrate concentration in groundwater was assessed, including predicting future WQ under different land uses by Gong et al. (2019), rather than relying solely on basic estimations. The CA-Markov model was used to predict land use by analyzing nitrogen and phosphorus correlating with various land uses. They found a significant positive correlation between nitrogen levels and sediment concentration, agricultural land area, river discharge, and urban area. Total phosphorus was also correlated with river flow, sediment yield, agricultural and urban area, as well as rice cultivation. Using CA-Markov model, the future budget of total nitrogen and phosphorus was estimated with future land use. Lee et al. (2022) improved biomass modeling by replacing the SWAT module with the CE-QUAL-W2 module in the algal bloom source code. Fang et al. (2024) combined machine learning with the SWAT model to pinpoint critical non-point pollution sources. They used self-organizing maps and stepwise regression to model variable relationships. ROC analysis set a forest cover threshold affecting WQ responses.

2.2.5 WQA simulation program (WASP)

WASP is a model applicabis a model applicable for one, two and three-dimensional systems developed by the US Environmental Protection Agency. It comprises different interactive systems of different nutrients, DO, BOD and phytoplankton. It can be developed for rivers, lakes, reservoirs, estuaries and coastal zones and integrated with hydrodynamic and/or sediment transport models to determine flow, depth, velocity, sediment concentration, and more (Wool et al., 2006). It solves the continuity equations (Equation (14)) with two kinetic modules, TOXI and EUTRO. These modules are for toxicants and conventional pollution, respectively.

\frac{\partial C}{\partial t} = - \frac{\partial U_{x} C}{\partial x} + \frac{\partial}{\partial x} (E_{x} \frac{\partial C}{\partial x}) - \frac{\partial U_{y} C}{\partial y} + \frac{\partial}{\partial y} (E_{y} \frac{\partial C}{\partial y}) - \frac{\partial U_{z} C}{\partial z} + \frac{\partial}{\partial z} (E_{z} \frac{\partial C}{\partial z}) + S_{L} + S_{B} + S_{K},

()

where C represents concentration, U is advective velocity, E is diffusion coefficient, S stands for loading rate, whereas suffixes L, B and K stand for direct or diffusive loading rate, boundary loading rate and loading rate from a source or sink, respectively.

The model considers pollutant transport through advection-dispersion processes, point and diffuse sources, boundary exchange, and sediment diagenesis in its latest version for accurate assessment (Martin & Wool, 2017). WASP was used to estimate the total maximum daily loads by addressing various pollutants. It was used to assess concentration profiles and analyzed Akkulam-Veli Lake for 15 months, estimating nitrate, phosphate, DO, BOD, and chlorophyll-a daily variations. WASP has several limitations, including isolating lake segments and overlooking their interactions. Bouchard et al. (2017) modified the WASP by incorporating particle collision rate and particle attachment efficiency to simulate the transport of carbon nanotubes (CNTs) in surface water. CNT concentration was evaluated in both the water and sediments. Mbuh et al. (2019) used WASP to conduct a sensitivity analysis revealing high sensitivity of phosphorus and DO concentrations during summer in terms of errors and model utility. They modeled chromium-III dispersion in the Bogota River, highlighting processes affecting WQPs (Ramos-Ramírez et al., 2020). Notably, the model indicated phosphorus as a phytoplankton limiter, CBOD decay reducing DO, and SOD as key in causing river hypoxia (Cashel et al., 2024).

2.2.6 Environmental fluid dynamics code

This model is capable of simulating hydrodynamics, sediment and contaminant transport and WQ components in one to three dimensions. It applies to rivers, reservoirs, lakes, estuaries, wetlands and coastal zones. The basic modeling framework consists of sigma or stretched vertical and Cartesian, orthogonal horizontal coordinates. The governing equation for pollutants consists of physical transport, advective-diffusive and kinetic processes. The model simulates concentrations of algae, organic carbon, phosphorus, nitrogen, silicon, COD, DO, total active metal and faecal coliform (Hamrick, 1996). Equation 15 is the governing equation used by the EFDC to evaluate the concentration profile of constituents.

\begin{array}{l} \frac{\partial}{\partial t} (m_{x} m_{y} H C) + \frac{\partial}{\partial x} (m_{y} H u C) + \frac{\partial}{\partial y} (m_{x} H v C) \\ + \frac{\partial}{\partial z} (m_{x} m_{y} w C) = \frac{\partial}{\partial x} \{\frac{(m_{y} H A_{x})}{m_{x}} \frac{\partial C}{\partial x}\} \\ + \frac{\partial}{\partial y} \{\frac{(m_{x} H A_{y})}{m_{y}} \frac{\partial C}{\partial y}\} + \frac{\partial}{\partial z} \{\frac{(m_{x} m_{y} A_{z})}{H} \frac{\partial C}{\partial z}\} + m_{x} m_{y} H S_{C}, \end{array}

()

where u, v and w are the velocity components, A represents the turbulent diffusivities with the directions in the suffix, S_c is the source and sink term calculated as per unit volume, H is the water column depth and m_x and m_y stand for the horizontal curvilinear coordinate scale factor.

The EFDC model mainly predicts waterbody WQPs under specific scenarios. Gong et al. (2016) used it to assess how rainfall and sewage leaks affect DO and various nutrient levels. Rainfall notably boosted total nitrogen and phosphorus concentrations. Sewage leaks led to increases in total nitrogen and phosphorus levels over time. The impact on chlorophyll-a was shorter in duration compared to the other parameters. In EFDC, eutrophication modeling, with sediment diagenesis, has been vital. Chen et al. (2016) studied this using different scenarios. The sediment diagenesis model mainly consists of three parts particulate organic matter (POM) deposition, diagenesis of POM and the resulting sediment fluxes returning inorganic nutrients to the water column. As algal blooms in reservoirs and other waterbodies are a major concern, EFDC is used to assess the relationship among hydrodynamics, WQ and algal blooms (Gao et al., 2018). Their study showed that water temperature and water age are influential factors in algal bloom. Integrating AI with the EFDC model boosts capabilities more. The multi-layered perceptron (MLP) was used to generate daily time series data from regular and daily monitored data. That generated data was fed into the EFDC model, which improved the model performance upstream (Kim et al., 2021). Shin et al. (2023) observed that WQ is primarily influenced by temperature, total phosphorus levels in inflow, discharge in the outlet, and wind speed for internal hydrodynamics. Across 19 stations, temperature was key in 8, while total phosphorus, solar radiation, outflow, total nitrogen, and TSS were influential in varying degrees at the other stations.

2.2.7 Limitations

Before applying WQM or making future modifications, it is important to note its limitations. First of all, WQM requires top-level skills and expertise in WQA. Physical system models typically include measurement error and structural uncertainties arising from lacking understanding of the physical mechanism. Performing uncertainty analysis enhances model result applicability accuracy. Uncertainty in WQMs arises from data quality and model structure. For example, Zhang et al. (2014) demonstrated that the resolution of the digital elevation model (DEM) affects SWAT model uncertainty. Higher DEM resolution leads to increased uncertainty in DO estimation. Lee et al. (2024) utilized input remotely sensed data from various sources to reduce uncertainty in SWAT. Masoumi et al. (2021) used the SUFI-2 algorithm to calibrate the CE-QUAL-W2 model by adjusting parameters related to water temperature and elevation. Xu et al. (2022) used generalized likelihood uncertainty estimation and regional sensitivity analysis (RSA) for the EFDC model implemented in the Three Gorges Reservoir. They identified sensitive parameters corresponding to the model variables. These examples highlight the importance of uncertainty estimation and sensitivity analysis for improving model results.

These research highlights the uncertainty in WQMs, serving as a limitation. Uncertainty varies in different environments and fluctuates with diverse input data. WQ model structures follow physical laws but use empirical equations for intermittent process evaluation involving parameters. This structure brings uncertainty since the empirical equation may deviate from the actual mathematics of the physical process. That is why calibration of sensitive parameters is done to make the model result more robust and closer to reality. In the domain of WQM, many developing countries lack standardization policies, posing an issue in ensuring consistency. Standardization of WQ models means evaluation of consistent guidelines for model development strategies because different models can produce different results while being applied on the same waterbody. This can occur due to considering different structures for empirical equations, incorporating additional processes or eliminating one with the assumption of non-significance, differences in governing equations are also a potential reason for the variations in model results. Therefore, the selection of a model without a standardized framework relies on data availability, computational effort, model accessibility, waterbody characteristics and simulation capabilities of WQPs.

2.3 WQM using AI

This study simultaneously focuses on deep learning (DL) applications in WQA, as DL has been used more frequently in the last 5 years compared to traditional ML methods mentioned in past reviews. The DL implications in forecasting and estimation of WQ variables have reached their peak in these years. This modeling foundation involves feature extraction, and analyzing temporal dependencies in time series data. Recent trends include hybridization and ensemble modeling. Figure 4 highlights key AI features in WQM applications.

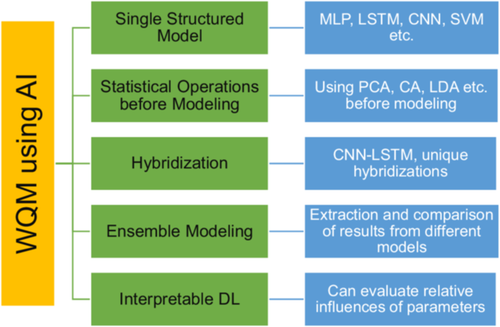
Solanki et al. (2015) applied DL in WQ forecasting using the deep belief network (DBN) and stacked denoising autoencoder (SdA) to predict lake parameters like DO, pH, and turbidity. In the DBN layer, adjacent layers are interconnected while units within each layer remain isolated. In the SdA network, data denoising is achieved by minimizing reconstruction errors in autoencoders. The network performance was compared with multilayer perceptron (MLP) and linear regression, which shows that the DL model efficiently handles data variability, underfitting issues and mitigates overfitting. The WQ research community is now using advanced models for predicting WQPs due to improved modeling abilities and new model introductions. Baek et al. (2020) used a long-short-term memory network (LSTM) to predict total nitrogen, phosphorus and organic carbon. LSTM, an upgraded recurrent neural network (RNN), is advantageous because it rectifies the vanishing gradient error inherent in RNN structure. Hence, LSTM is the optimal model for time-series data and is used in WQPs time-series modeling.

Blue-green algae Chl-a, fluorescent dissolved organic matter, DO, specific conductance and turbidity were estimated by progressively decreasing deep neural network (DNN). Results were compared with SVR, MLR and extreme learning machine regression. The input to the models was 20 spectral features from image processing and spatial operations. The DNN performed the best with a mean R² of 0.89. Zhi et al. (2021) fed sparse DO data and daily hydro-meteorological data into the LSTM model. Here, 74% of the study area showed Nash–Sutcliffe efficiency above 0.4. The model excelled in low DO variability zones but struggled with peaks and troughs. Preprocessing data using statistical operations to extract key features or manage missing data has also been applied in multiple studies. Dilmi and Ladjal (2021) applied principal component, linear discriminant and independent component analyses for feature extraction from WQ data. Then, the LSTM and SVM were used as WQ classifiers for qualitative decision-making of WQ condition. Zhou (2020) used a multivariate Bayesian uncertainty processor to link ANN-simulated and observed WQ data. The output provided a probabilistic forecast using a Monte Carlo simulation, indicating uncertainty.

Along with this, LSTM and transfer learning LSTM (TL-LSTM) were implemented to address the missing data issue of rate 0.5. The TL-LSTM transferred the knowledge from the reference temporal sequence. Bi et al. (2024) used the Savitzky-Golay filter to eliminate noise from the WQ data set and then fed it into LSTM-based encoder-decoder generative NN to predict the DO and COD. Mokarram et al. (2024) used geostatistical methods to prepare WQ maps and develop fuzzy membership functions for qualitative analysis of spatial distribution. Different models like LSTM, MLP, SVR, and RBF were used to predict EC, turbidity, Chl-a, TSS, Mg, and Na. Hybrid models, introduced in the last half-decade, are now widely used in various studies. Barzegar et al. (2020) used a convolutional neural network (CNN), LSTM and a hybrid CNN-LSTM to predict DO and Chl-a from time series data of EC, oxidation–reduction potential, pH and temperature. Time-lagged input data was used in DL and hybrid models. CNN can extract features from data series, while LSTM models temporal dependencies. By combining CNN and LSTM, this study reduced the root mean absolute error for predicting DO and Chl-a.

Prasad et al. (2022) found that the CNN-LSTM hybrid outperforms stand-alone CNN and LSTM models in their comparison study. Khullar and Singh (2022) used free ammonia, DO, coliform, pH, nitrogen, and temperature in a hybrid CNN and BiLSTM model to predict BOD and COD. In BiLSTM, an extra LSTM layer changes the time-series data flow direction compared to LSTM. This CNN-BiLSTM hybrid excelled in WQP prediction over ANN, SVM, CNN and LSTM. Rasheed Abdul Haq and Harigovindan (2022) compared CNN-LSTM and CNN-GRU hybrid models to forecast salinity, pH, DO, and temperature, favoring CNN-LSTM. They tuned hyperparameters using two separate WQ datasets. Wan et al. (2022) used a hybridization approach, simulation observation difference-visual geometry-LSTM to model WQPs by extracting the multidimensional spatial features of a watershed. The SOD modular using Equation (13) was used to simulate the concentrations of nutrients. LSTM was fed with hydro-meteorological and spatial time series features to predict errors. This error model, incorporating spatial and environmental conditions, outperformed ARIMA, SVR, and RNN models in accuracy. Yu et al. (2022) used another hybrid model processing combining data decomposition, fuzzy c-means clustering and bidirectional gated recurrent unit (BiGRU). They decomposed WQ data into subseries with empirical wavelet transform, recombined using fuzzy c-means clustering, and employed BiGRU to predict DO and NH₃-N. Han et al. (2023) introduced CRn-BEATS, a hybrid model for pH, turbidity, and temperature prediction. Compared to LSTM, LSTnet, GNN, ConvLSTM, and N-BEATS, CRn-BEATS demonstrated the best performance. The model comprised three blocks with fully connected LSTM layers. Ensemble modeling merged results from various models to enhance accuracy. Zamani et al. (2023) used ensemble learning, combining RNN, LSTM, GRU, and temporal convolutional network DL models to predict Chl-a. They utilized genetic algorithms for weighted averaging. Predictors included pH, oxidation–reduction potential, temperature, EC, and DO. While GRU excelled individually, ensemble modeling outperformed by leveraging diverse models. Notably, interpretable DL marks a significant advancement in WQM. Zheng et al. (2023) used the Shapley additive explanations (SHAP) method to interpret the prediction results of WQPs. Meteorological, land-use and socioeconomic parameters were used in a five-layered feed-forward network. NH₃-N, DO, and TN, air temperature, forest area, grain production, population density and urban area were the influencing factors in predicting COD. This interpretation technique may calculate prediction changes with and without input parameters.

2.3.1 Limitations

DL methods aimed at model WQPs offer ample potential for uncovering hidden patterns in natural systems. DL models excel at capturing nonlinear variable relationships, offering modelers increased flexibility in their modeling approach. The limitations of DL modeling lie in the training processes. DL model training requires vast data to optimize weights and biases across network layers effectively. The more complex the model, the higher the number of trainable parameters. DL models require adjustments to their hyper-parameters for optimal results. DL models suffer from the inability to generalize the input-output relationship due to the complexity of the internal mathematical operations. That is why the scientific communities in various fields are including physical laws in DL models like physics-informed neural networks (PINNs) to decrease data and computational needs and improve the generalization for datasets outside the training range. SHAP-like frameworks are also executed to interpret the relative impacts of different factors on WQPs. The results of DL models are uncertain due to input data quality and model structure.

Rahat et al. (2023) used the Monte Carlo dropout method for model uncertainty estimation, finding it boosts LSTM network generalization in WQM. Sensitivity analysis is key for DL models in WQM. A flawed selection of parameters can mislead the model, affecting results. Yu et al. (2024) used Sobol's and hierarchical sensitivity analyses to determine key parameters and processes influencing redox zonations in riparian areas. The study highlighted the significance of sensitivity analysis in DL models for reliable WQ status predictions. Hence, DL models lack generalization ability and do not have a built-in strategy to identify parameters and estimate uncertainty, which is a significant limitation of this approach.

3 COMPARATIVE DISCUSSION

This study discusses three methods for expressing WQ conditions - WQ indexing, WQM, and WQM using AI with a focus on DL with corresponding applications. Each method involves specific inputs and outcome derivation processes, each evaluated differently based on performance.

In WQ indexing, WQPs serve as primary inputs. As mentioned in earlier sections, the process of parameter selection has progressed to develop a better index model. The WQM requires hydrologic, hydrodynamic, and climatic parameters as input with the initial concentration of several pollutants and parameters. In WQM with AI, input includes direct parameter values mainly, but also considers various types such as spectral features with the potential for other types. So, it can be said that the WQM requires the most versatile data set. It is probably the most expensive one in the practical field but very specific in terms of the requirement which is not the case for the other two types as the issues of subjectivity come because of using presumptions.

The processing methods differ in each approach. WQ indexing involves a series of mathematical operations to get to the final result. Sub-index generation, weight assignment and aggregation are the steps for evaluating the final index value. WQM uses numerical schemes to solve equations related to the physical processes of water bodies, yielding the final results. In WQM using AI, steps include choosing a model, inputting data, and evaluating performance with indicators. In all three methods, outcomes include determining an index value, evaluating a concentration map, and obtaining a direct parameter value. Each of these represents a unique expression of the WQ status. Through indexing, no prediction can be done using variant environmental conditions unless the index is related to parameters non-related to WQ. For WQM using AI to produce the same results as WQPs, their inputs must match. Measurement of parameters is essential for running these two methods. Once calibrated and validated, the WQM model can repetitively operate in various scenarios. The analysis of water pollution susceptibility using these three methods is also scattered. Indexing reveals the key WQPs that affect the WQ index value significantly during susceptibility analysis. AI-driven WQM continues evolving with emerging applications to interpret DL results as addressed in earlier sections. In WQM, both parameters and dominant processes driving WQ changes can be accurately identified.

Performance evaluation is crucial for assessing WQM and WQM with AI using statistical measures to analyze their explicit parameter values. However, evaluating WQ indexing is challenging as the index value is not a physical parameter, requiring expert opinions and domain knowledge for assessment. Therefore, it is important to choose the most efficient WQ analysis method based on objectives. WQ indexing can be used for overall quality and pollution assessment, identifying key parameters. WQM is a useful strategy for addressing WQ changes and pollution. It can also aid in predicting unexperienced conditions for the waterbody. WQM using AI is a developing sector, finding applications in new domains with progress. This method excels when predicting specific parameters based on observed values or environmental variables. Table 1 summarizes the three WQA strategies in a comparative discussion.

TABLE 1. Comparative discussion of WQA strategies.

WQA technique

Input data requirement

Processing

Advantages

Limitations

WQI

−
Concentrations of WQPs.

−
Sub-index generation (by expert knowledge or statistical analysis).
−
Weight assignment (by expert knowledge or statistical analysis).
−
Aggregation (by statistical or ML-based methods).

−
Low computational effort is required.
−
Input data requirement is limited to WQPs.
−
Good for comparative assessments among parts of river stretches.

−
Prone to subjectivity errors.
−
Nonlinearity between parameter concentration and index values is not considered in most of the cases.
−
Ca not exhibit the dynamic nature of quality alterations.

WQM

−
Initial state of WQP concentrations.
−
Flow of the river (volume in case of static waterbody).
−
Hydrodynamic data (velocity, depth).
−
Climatic parameters (temperature, wind speed, solar radiation, humidity etc.).

−
By solving series of physically and empirically based equations in lumped or discretized framework.

−
Based on physical equations expressing the natural system.
−
Dynamic features are included.
−
Robust expression of quality distribution along a river stretch.

−
Vast amount of input data is required.
−
Computational skill requirement is high.

WQM using AI

−
Mainly WQP concentration data.
−
Other hydrologic or hydrodynamic property-related data according to the modeling strategy adopted.

−
Preparation of the modeling scheme.
−
Development of model architecture.
−
Model training.

−
Nonlinearity between quality parameters is introduced.
−
High degrees of freedom in modeling scheme determination
−
Multi-dimensional input can be incorporated easily.

−
“Black box” model not exhibiting physical insights about the system.
−
May be subjected to overfitting and modeling unrealistic relationships.

3.1 Performance metrics

Performance assessment is crucial in all modeling. Model performances are mainly evaluated using statistical measures of modeled and observed variables. The three WQA approaches examined in this study have unique methods and performance assessments. In WQI modeling, it is crucial to note that the model's output is a numerical value, not a physical measurement. WQI values for waterbodies are often categorized into classes like “excellent,” “good,” “fair,” and “bad.” There is no universally accepted scheme for this classification because different WQI models use varying stratifications.

In literature, scholars discussed the “metaphoring problem,” where the same quality properties can have various interpretations. The scientific community mainly uses two strategies to establish accurate values for WQI. One approach involves comparing new model results with established WQI models using metrics like coefficient of determination (R²), mean squared error (MSE), root MSE, and mean absolute error to evaluate accuracy. These performance metrics are utilized solely for WQI development in a regression context. Secondly, the WQ is classified based on the number of quality parameters that surpass the acceptable level mentioned earlier.

Uddin, Jackson, et al. (2023) proposed a universal scheme for WQA. This scheme categorizes WQ as “excellent” when no parameters fail and “bad” when all parameters fail, with two intermediate classes in between. This approach transforms WQI development into a classification task. Evaluation metrics used in this classification context include ROC curve, binary cross-entropy, kappa index, and accuracy, precision, and specificity from the confusion matrix. A modeler must understand the data framework of the study area to decide if WQI development should be approached as a regression or classification problem. The challenge in evaluating WQI model performance lies in determining accurate “true values,” as using a previous model result can introduce subjectivity due to inherent error structures. Uddin et al. (2022) and Uddin, Nash, et al. (2023) validated a new ML-based WQI models against conventional models, with a focus on an extreme gradient boosting (XGB) model. Results of root MSE (~3) and R² (~0.9) indicated a good performance. Uddin, Rahman, et al. (2023) found that the weighted quadratic mean and unweighted RMS-WQI models exhibit a greater resemblance to the newly developed XGB model.

Uncertainty analysis is implemented for the performance assessment of WQI. In WQM, assessment is more straightforward using regression metrics. Given the global widespread use of WQMs, we highlight performance in key studies across diverse locations to inform future modelers. For example, Abbaspour et al. (2015) used the SWAT across Europe, simulating nitrate levels only at 14 Danube basin stations due to limited data availability. R² for nitrate ranged from 0.2 to 0.65, influenced by unknowns like fertilizer usage which was the main reason for nitrate leaching beyond the root zone. The SWAT simulation of fertilizer application, while accurate for requirements, underestimates channel nitrate concentrations due to overlooking overuse. Woo et al. (2021) applied the SWAT WQM in an interbasin water transfer scenario, achieving R² values above 0.6 for all cases, demonstrating good simulation capabilities in this specific context.

Zhang et al. (2013) applied SWAT in different regulated basins in China, finding that WQ simulation is more effective in reservoirs compared to sluice gates due to the absence of pollutant transport mechanisms under sluice gates in SWAT. Saravanan et al. (2023) successfully modeled ammoniacal and nitrate nitrogen in India with good calibration results. However, performance declined in validation, indicating reality was not captured. This mirrors the European case, where the SWAT model underestimates channel nutrient levels due to unknown fertilizer applications. Also in USA, Zeiger and Hubbart (2016) revealed SWAT model shortcomings in nutrient loading estimation, emphasizing the significance of knowing fertilizer quantities for accurate predictions.

The SWAT model overlooks baseflow temporal quality changes, leading to errors in pollution loading estimates. To improve accuracy, efforts have been made to integrate SWAT with groundwater and contaminant transport models. The CE-QUAL-W2 model, more commonly used in reservoirs than rivers and other channels, is now being integrated with models like SWAT and SWMM to incorporate flow patterns for quality modeling in rivers. Its performance in reservoirs is influenced by various factors. Benicio et al. (2024) found high accuracy (R² > 0.9) for water temperature and level simulations, but nutrient and DO predictions vary due to organic matter, algal properties, and data quality. Studies show CE-QUAL-W2 performs better forecasting phosphorus in dry seasons than in summer. Therefore, climatic factors significantly impact the modeling process.

Burigato Costa et al. (2019) reviewed six WQMs, noting the prevalence of CE-QUAL-W2 in the USA, Iran, and China. It is critiqued in South Korea but performs well in India. Modelers should consider process complexities and if the model addresses them. AQUATOX assesses contaminants' impact on ecosystems in rivers and lakes, requiring biomass quantification for calibration and validation. In River Thames, Lombardo et al. (2015) found a 1.6% and 2.3% biomass variation when using the AQUATOX model to evaluate triclosan and linear alkyl benzene sulfonate impact. Zhang et al. (2018) and Zhang and Liu (2014) used the model in two Chinese lakes, yielding satisfactory results.

However, it is important to note that the database needed for developing and calibrating the model is unique and often unavailable in developing countries, limiting its global applicability. For the WASP model, literatures suggest that a sufficiently long observed data set obtained from the field enhances simulation accuracy. The model performance in Shenandoah River was fluctuating when predicting DO, Chl-a, N, and P due to data unavailability (Mbuh et al., 2019). The WASP model for Lushui River was calibrated with observed data over 12 months, showing a good fit (Obin et al., 2021). Properly calibrating model parameters using observed data is important for the success of the WASP model.

The EFDC model is commonly used to predict Chl-a levels along with other quality parameters in water bodies. Gong et al. (2016) observed a 33.3% relative RMSE for predictions of Chl-a, DO, temperature, and total phosphorous, indicating the model's accuracy in simulations. Kim et al. (2017) found EFDC model predicts better in low Chl-a areas. They emphasized growth characteristics of different algal groups to enhance simulation accuracy in high-concentration zones.

The versatility of DL techniques of WQM stems from diverse model structures, input-output frameworks, and hyper-parameter adjustments. Therefore, discussing the performance metrics of different networks in various scenarios is crucial for the research community. Li et al. (2019) preferred time-series WQM using RNN with improved Dempster-Shafer evidence theory to predict the WQPs in two setups. Single and multiple time-step predictions showed decreasing accuracy with longer time lags, regardless of the complexity of the RNN structure. Prasad et al. (2022) used 12 WQPs with CNN, LSTM, and AutoDL to predict WQ status in an Indian lake. They structured the input-output model in binary and multiple classes, with CNN displaying superior feature extraction compared to LSTM and AutoDL. However, if approached as a regression task, CNN's advantage might not hold. Additionally, DL effectively predicted WQ in chemically ungauged rivers. Zhi et al. (2023) used LSTM to predict DO for 580 rivers in the USA with input from temperature, light, and flow. They chemically gauged 480 rivers and left 100 rivers ungauged within specific regions. The LSTM model achieved NSE between 0.5 and 0.72 for ungauged rivers in the western and north-eastern regions, indicating prediction accuracy in data-scarce zones with varying performance metrics and uncertainties.

3.2 WQA practices across different countries

It is important to test how different WQA methods perform under various environmental and climatic conditions to understand their effectiveness. Factors like government regulations, data availability, and public attitude also influence the methodological choice of the scientific community. Here, we have explored the SCOPUS database to get insights into research article counts published in the aspect of different countries on all WQA approaches. Figures 5-7 show the detailed geographic variations.

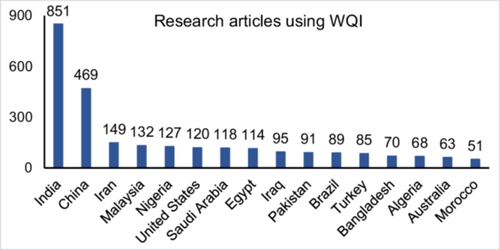
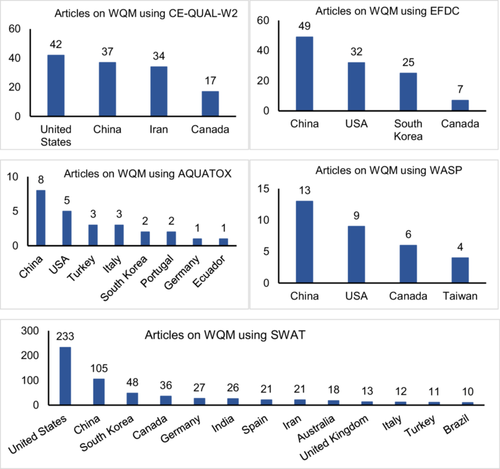
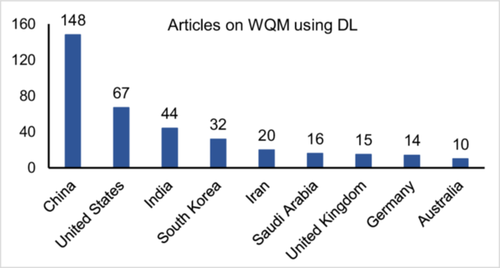
The total number of documents is evaluated by providing suitable keywords in the search engine. The keywords used are water quality index, CE QUAL W2, Aquatox, EFDC, WASP and water quality, SWAT and water quality, deep learning, and WQM. The total number of articles found is 1825, 115, 25, 135, 37, 521, and 374, respectively. This figure displays articles published by countries with significant numbers in the domain from 2014 to 2024. It can be seen that the WQI being the most applied WQA strategy is hugely executed in the developing countries even much more than the developed countries. Chidiac et al. (2023) stated a similar statement describing the intent of the developing nations in analyzing the WQ using WQI, which indicates how the WQ status of rivers and lakes is crucial to the socioeconomic development. For example, Botle et al. (2023) found significant heavy metals polluted 21 Indian rivers, posing carcinogenic risks to children and adults. The toxicity was also increasing due to high levels of heavy metals exceeding acceptable limits.

In case of WQM using various models, China and the USA have the most number of articles. Only in the case of SWAT, the execution is higher than in other WQMs. The possible reason behind this disparity may be the availability of data. As the WQMs require a huge and versatile data set for model development and calibration, it has not been adopted by many in the developing world (though China is a developing country), where data availability and data collection are big challenges for infrastructural and financial issues. For example, by exploring the SCOPUS database it can be found that in USA a total of 835 studies have utilized SWAT and among them, 233 are with the objective of WQA and other 602 studies have been done for hydrological modeling (quantitative analysis of river flow) indicating almost 28% of studies using SWAT are for WQ study. The same SWAT model when comes to India, only 7.56% of studies are with the objective of WQA. Only 26 studies among 344 utilizations of SWAT approached for WQ.

Hence, it can be said that even with satisfying knowledge and technical expertise resources, the developing countries are unable to apply the WQM because of lacking data availability and infrastructure. Along with this, WQM using AI is being started to develop as a viable methodology for the whole world. But as discussed earlier, the results of WQI or even WQM using AI have certain limitations, which do not depict the physical processes and are prone to many kinds of error, and the data requirement for DL models is also high because of the complex model training processes. This issue can reduce its implications in developing countries. For example, Nishat et al. (2025) implemented 14 ML models in four rivers of Bangladesh and obtained satisfactory model results, but BOD and COD were not considered as input parameters of the models because of the unavailability of data, which reduces the model application substantially. Hence, the countries that are focusing on developing research on WQA should focus on an increase in WQM applications.

4 FUTURE TRENDS

The future of WQA lies in exploring the distinct trends of its three approaches: WQI, WQM, and WQM using AI. The WQI development has been extensively focused on drinking purposes. However, water consumption today includes multiple areas such as irrigation, aquaculture, industrial requirements, and recreational uses. A comprehensive WQI framework for these diverse purposes will enhance its practicality. New parameters and standard permissible values shall be adjusted based on water consumption needs. One upcoming challenge is assessing the relationship between water ecosystems and characteristics like hydrological, hydrodynamic, and chemical for quality maintenance. Exploring this relationship can integrate the role of microalgae in developing WQI.

Another key research goal is to create a globally accepted classification system that categorizes WQ effectively. Developing WQI requires labor-intensive raw data collection, consuming significant time and economic resources. Most studies collect data daily within a specific time range. However, the quality variables show notable diurnal changes that can impact the overall WQ. For example, the DO changes with temperature, impacting nutrient and organic matter concentrations. Therefore, a real-time data system for WQI assessment can improve quality by capturing temporal variations effectively. The future WQ indexes should prioritize inclusivity and robustness concerning waterbody health. For habitat suitability, the depth and velocity of rivers play a crucial role as specific species need certain conditions for growth. These hydrodynamic factors should be considered in the WQI framework alongside WQPs.

In the context of WQMs, there is a clear gap in literature on the future development directions. WQMs, rooted in mathematical equations, advance through discoveries of relationships among natural elements. For example, the atmospheric deposition module of present WQMs has been incorporated only after the physics behind this process has been explored by the scientific community. That is why, a future need rather than a future direction can be stated for WQMs. The matter of pollution stress on waterbodies is driven by anthropogenic and climatic factors together. The segmentation of this joint impact is one of the key understandings that the scientific community and the policymakers want to develop.

Adding a pollutant without increasing the pollution load, but with reduced discharge, can change a river from clean to contaminated. The decline in discharge can result from both climatic and/or anthropogenic factors. So, future WQ management needs to consider both these factors together. While climate variables are commonly included in WQMs, anthropogenic factors such as water withdrawal from rivers and aquifers should also be incorporated in modeling structures. Including more ecological state variables in the WQM framework can show how WQ affects the habitat suitability of various species. Sediment diagenesis in WQ models is mainly unaffected by waterbody hydrodynamics, as it is a significant issue in static environments like lakes and reservoirs. However, recent studies show this process occurs significantly in dynamic waterbodies, affecting sediment transport and diagenesis even with hydrodynamic influences. Therefore, the inclusion of hydrodynamic state variables in the diagenesis equation is necessary and should be addressed in future.

The future directions in WQM with AI should distinguish themselves from general ML model progress. Many previous literatures have focused on smart hyper-parameter tuning, the development of globally acceptable generic network architecture, and the utilization of different optimization algorithms as future directions of WQM using AI. These improvements enhance ML models across all domains where they perform well. In the future, AI can enhance WQM by refining WQA, often by utilizing ML models to link WQPs. Before applying the ML model, it should be understood whether the parameters have any relationship according to the available knowledge of chemistry. If the parameters are not related, then a wide range of data must be tested in different geographical locations to increase the dependability of ML models in WQM. Incorporating physical laws in ML models can also yield good results without requiring a large amount of data. PINNs can be used for even parameter estimation, as they consider the governing differential equations as the loss function of the ML model.

5 CONCLUSIONS

This study elaborates on three methodologies adopted by the scientific community for WQ analysis. The three methods are WQ indexing, WQM, and WQM using AI. The description of the model development procedures, initial requirements, drawbacks and advantages, field of application, and future trends of each method have been highlighted in this study. A comparative discussion among the aforementioned three methods has also been included, which is a novel attempt till now as per our knowledge.

This study highlights the problems one may face while adopting any of these three methods of WQ analysis. The set of parameters to be selected is one of the major problems in WQI development, which is addressed by statistical schemes like-PCA by many across the globe. The use of a FIS has provided the opportunity to get optimized values of weights and sub-indices in WQI development. The use of ML models is also paving the way for nonlinear aggregations of WQPs to evaluate WQI. On the other hand, the WQM is becoming more sophisticated by integrating other environmental process models and incorporating various processes occurring inside waterbodies, which influence the WQ. Attempt to develop the concept regarding the process of sediment diagenesis by exploring the role of many water parameters affecting the process has been attempted by many. The hydrodynamic part and surface water-groundwater interaction have the opportunity to be focused more for better predictions of WQ. Lastly, the WQM using AI is still an emerging field to predict a single or a set of WQPs. In most of the studies in the last 5 years, time-series data of WQPs have been used to predict the same or other WQPs using AI. Few studies of taking socioeconomic factors and other environmental variables as input have also been done to draw novel relationships and optimized management plans. The use of CNN-LSTM hybrid has emerged as a successful modeling scheme while being experimented on around the world.

This study concludes another important point to lead researchers and practitioners regarding the choice of methodologies for WQ analysis. As the comparative discussion suggests, the WQI, WQM and modeling using AI have a very distinct domain of application. These three methods can be adopted with an objective of assessment of status, process understanding, and single or a set of parameter predictions respectively. So, the objective of the study can lead to the choice of the methodology to be adopted.

ACKNOWLEDGMENTS

The Science and Engineering Research Board, Government of India is acknowledged for funding this study under the State University Research Excellence (SURE) Project (SUR/2022/001557).

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

ETHICS STATEMENT

None declared.

Open Research

DATA AVAILABILITY STATEMENT

The data used for the research are described in the article.

REFERENCES

Abbaspour, K. C., Rouholahnejad, E., Vaghefi, S., Srinivasan, R., Yang, H., & Kløve, B. (2015). A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. Journal of Hydrology, 524, 733–752.
10.1016/j.jhydrol.2015.03.027
Web of Science® Google Scholar
Afshar, A., Feizi, F., Moghadam, A. Y., & Saadatpour, M. (2017). Enhanced CE-QUAL-W2 model to predict the fate and transport of volatile organic compounds in water body: Gheshlagh reservoir as case study. Environmental Earth Sciences, 76, 803.
10.1007/s12665-017-7108-5
Web of Science® Google Scholar
Akkoyunlu, A., & Karaaslan, Y. (2015). Assessment of improvement scenario for water quality in Mogan Lake by using the AQUATOX model. Environmental Science and Pollution Research, 22(18), 14349–14357.
10.1007/s11356-015-5027-0
CAS PubMed Web of Science® Google Scholar
Arnold, J. G., Moriasi, D. N., Gassman, P. W., Abbaspour, K. C., White, M. J., Srinivasan, R., Santhi, C., Harmel, R. D., van Griensven, A., Van Liew, M. W., Kannan, N., & Jha, M. K. (2012). SWAT: Model use, calibration, and validation. Transactions of the ASABE, 55(4), 1491–1508.
10.13031/2013.42256
Web of Science® Google Scholar
Arnold, J. G., Srinivasan, R., Muttiah, R. S., & Williams, J. R. (1998). Large area hydrologic modeling and assessment part I: Model development 1. JAWRA Journal of the American Water Resources Association, 34(1), 73–89.
10.1111/j.1752-1688.1998.tb05961.x
CAS Web of Science® Google Scholar
Arora, S., & Keshari, A. K. (2021). Pattern recognition of water quality variance in Yamuna River (India) using hierarchical agglomerative cluster and principal component analyses. Environmental Monitoring and Assessment, 193(8), 494.
10.1007/s10661-021-09318-1
CAS PubMed Web of Science® Google Scholar
Aydin, H., Ustaoğlu, F., Tepe, Y., & Soylu, E. N. (2021). Assessment of water quality of streams in northeast Turkey by water quality index and multiple statistical methods. Environmental Forensics, 22(1–2), 270–287.
10.1080/15275922.2020.1836074
CAS Web of Science® Google Scholar
Baek, S. S., Pyo, J., & Chun, J. A. (2020). Prediction of water level and water quality using a CNN-LSTM combined deep learning approach. Water, 12(12), 3399.
10.3390/w12123399
CAS Web of Science® Google Scholar
Bai, J., Zhao, J., Zhang, Z., & Tian, Z. (2022). Assessment and a review of research on surface water quality modeling. Ecological Modelling, 466, 109888.
10.1016/j.ecolmodel.2022.109888
CAS Web of Science® Google Scholar
Barzegar, R., Aalami, M. T., & Adamowski, J. (2020). Short-term water quality variable prediction using a hybrid CNN–LSTM deep learning model. Stochastic Environmental Research and Risk Assessment, 34(2), 415–433.
10.1007/s00477-020-01776-2
Web of Science® Google Scholar
Benicio, S. H. M., Basso, R. E., & Formiga, K. T. M. (2024). Global applications of the CE-QUAL-W2 model in reservoir eutrophication: A systematic review and perspectives for Brazil. Water, 16(24), 3556.
10.3390/w16243556
CAS Web of Science® Google Scholar
Bi, J., Yuan, H., Li, S., Zhang, K., Zhang, J., & Zhou, M. (2024). Arima-based and multiapplication workload prediction with wavelet decomposition and Savitzky–Golay filter in clouds. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 54(4), 2495–2506.
10.1109/TSMC.2023.3343925
Web of Science® Google Scholar
Bordalo, A. A., Teixeira, R., & Wiebe, W. J. (2006). A water quality index applied to an international shared river basin: The case of the Douro River. Environmental Management, 38, 910–920.
10.1007/s00267-004-0037-6
PubMed Web of Science® Google Scholar
Botle, A., Salgaonkar, S., Tiwari, R., Ambadekar, S., & Barabde, G. R. (2023). Brief status of contamination in surface water of rivers of India by heavy metals: A review with pollution indices and health risk assessment. Environmental Geochemistry and Health, 45(6), 2779–2801.
10.1007/s10653-022-01463-x
CAS PubMed Web of Science® Google Scholar
Bouchard, D., Knightes, C., Chang, X., & Avant, B. (2017). Simulating multiwalled carbon nanotube transport in surface water systems using the Water Quality Analysis Simulation Program (WASP). Environmental Science & Technology, 51(19), 11174–11184.
10.1021/acs.est.7b01477
CAS PubMed Web of Science® Google Scholar
Brown, R. M., McClelland, N. I., Deininger, R. A., & Tozer, R. G. (1970). A water quality index-do we dare. Water and Sewage Works, 117(10), 339–343.
Google Scholar
Burigato Costa, C. M. S., da Silva Marques, L., Almeida, A. K., Leite, I. R., & De Almeida, I. K. (2019). Applicability of water quality models around the world—a review. Environmental Science and Pollution Research, 26, 36141–36162.
10.1007/s11356-019-06637-2
PubMed Google Scholar
Cashel, F. S., Knightes, C. D., Lupo, C., Iott, T., Streich, K., Conville, C. J., Bridges, T. W., & Dombroski, I. (2024). Using monitoring and mechanistic modeling to improve understanding of eutrophication in a shallow New England estuary. Journal of Environmental Management, 355, 120478.
10.1016/j.jenvman.2024.120478
CAS PubMed Web of Science® Google Scholar
CCME. (2001). Canadian water quality guidelines for the protection of aquatic life: CCME Water Quality Index 1.0 (Technical Report). Canadian environmental quality guidelines, 1999, Canadian Council of Ministers of the Environment.
Google Scholar
Chen, L., Yang, Z., & Liu, H. (2016). Assessing the eutrophication risk of the Danjiangkou Reservoir based on the EFDC model. Ecological Engineering, 96, 117–127.
10.1016/j.ecoleng.2016.02.021
Web of Science® Google Scholar
Chidiac, S., El Najjar, P., Ouaini, N., El Rayess, Y., & El Azzi, D. (2023). A comprehensive review of water quality indices (WQIs): History, models, attempts and perspectives. Reviews in Environmental Science and Bio/Technology, 22(2), 349–395.
10.1007/s11157-023-09650-7
CAS PubMed Web of Science® Google Scholar
Cole, T. M., & Wells, S. A. (2006). CE-QUAL-W2: A two-dimensional, laterally averaged, hydrodynamic and water quality model, version 3.5 (Instruction Report EL-06-1). US Army Engineering and Research Development Center.
Google Scholar
Cude, C. G. (2001). Oregon water quality index a tool for evaluating water quality management effectiveness. JAWRA Journal of the American Water Resources Association, 37(1), 125–137.
10.1111/j.1752-1688.2001.tb05480.x
CAS Web of Science® Google Scholar
Dilmi, S., & Ladjal, M. (2021). A novel approach for water quality classification based on the integration of deep learning and feature extraction techniques. Chemometrics and Intelligent Laboratory Systems, 214, 104329.
10.1016/j.chemolab.2021.104329
CAS Web of Science® Google Scholar
Ding, F., Zhang, W., Cao, S., Hao, S., Chen, L., Xie, X., Li, W., & Jiang, M. (2023). Optimization of water quality index models using machine learning approaches. Water Research, 243, 120337.
10.1016/j.watres.2023.120337
CAS PubMed Web of Science® Google Scholar
Dobbins, W. E. (1964). BOD and oxygen relationships in streams. Journal of the Sanitary Engineering Division, 90(3), 53–78.
10.1061/JSEDAI.0000495
Google Scholar
Dojlido, J., Raniszewski, J., & Woyciechowska, J. (1994). Water quality index applied to rivers in the Vistula river basin in Poland. Environmental Monitoring and Assessment, 33, 33–42.
10.1007/BF00546659
CAS PubMed Web of Science® Google Scholar
Dutta, S., Dwivedi, A., & Suresh Kumar, M. (2018). Use of water quality index and multivariate statistical techniques for the assessment of spatial variations in water quality of a small river. Environmental Monitoring and Assessment, 190(12), 718.
10.1007/s10661-018-7100-x
PubMed Web of Science® Google Scholar
Elçi, A., Ayaz, S., & Aynur, Ş. (2018). Simulating the impact of water quality improvement measures for nutrient-sensitive river basins with the Aquatox model. EPiC Series in Engineering, 3, 651–658.
10.29007/5q94
Google Scholar
Epelde, A. M., Cerro, I., Sánchez-Pérez, J. M., Sauvage, S., Srinivasan, R., & Antigüedad, I. (2015). Application of the SWAT model to assess the impact of changes in agricultural management practices on water quality. Hydrological Sciences Journal, 60(5), 1–19.
10.1080/02626667.2014.967692
Google Scholar
Ewaid, S. H., & Abed, S. A. (2017). Water quality index for Al-Gharraf River, Southern Iraq. Egyptian Journal of Aquatic Research, 43(2), 117–122.
10.1016/j.ejar.2017.03.001
Google Scholar
Fang, S., Deitch, M. J., Gebremicael, T. G., Angelini, C., & Ortals, C. J. (2024). Identifying critical source areas of non-point source pollution to enhance water quality: Integrated SWAT modeling and multi-variable statistical analysis to reveal key variables and thresholds. Water Research, 253, 121286.
10.1016/j.watres.2024.121286
CAS PubMed Web of Science® Google Scholar
Fathi, E., Zamani-Ahmadmahmoodi, R., & Zare-Bidaki, R. (2018). Water quality evaluation using water quality index and multivariate methods, Beheshtabad river, Iran. Applied Water Science, 8(7), 210.
10.1007/s13201-018-0859-7
Web of Science® Google Scholar
Gani, M. A., Sajib, A. M., Siddik, M. A., & Md Moniruzzaman, M. (2023). Assessing the impact of land use and land cover on river water quality using water quality index and remote sensing techniques. Environmental Monitoring and Assessment, 195(4), 449.
10.1007/s10661-023-10989-1
CAS PubMed Web of Science® Google Scholar
Gao, L., & Li, D. (2014). A review of hydrological/water-quality models. Frontiers of Agricultural Science and Engineering, 1(4), 267.
10.15302/J-FASE-2014041
Google Scholar
Gao, Q., He, G., Fang, H., Bai, S., & Huang, L. (2018). Numerical simulation of water age and its potential effects on the water quality in Xiangxi Bay of Three Gorges Reservoir. Journal of Hydrology, 566, 484–499.
10.1016/j.jhydrol.2018.09.033
CAS Web of Science® Google Scholar
Gazzaz, N. M., Yusoff, M. K., Ramli, M. F., Juahir, H., & Aris, A. Z. (2015). Artificial neural network modeling of the water quality index using land use areas as predictors. Water Environment Research, 87(2), 99–112.
10.2175/106143014X14062131179276
CAS PubMed Web of Science® Google Scholar
Giri, S. (2021). Water quality prospective in twenty first century: Status of water quality in major river basins, contemporary strategies and impediments: A review. Environmental Pollution, 271, 116332.
10.1016/j.envpol.2020.116332
CAS PubMed Web of Science® Google Scholar
Goher, M. E., Hassan, A. M., Abdel-Moniem, I. A., Fahmy, A. H., & El-Sayed, S. M. (2014). Evaluation of surface water quality and heavy metal indices of Ismailia Canal, Nile River, Egypt. Egyptian Journal of Aquatic Research, 40(3), 225–233.
10.1016/j.ejar.2014.09.001
Google Scholar
Golomb, D., Ryan, D., Underhill, J., Wade, T., & Zembar, S. (1997). Atmospheric deposition of toxics onto Massachusetts Bay—II. Polycyclic aromatic hydrocarbons. Atmospheric Environment, 31(9), 1361–1368.
10.1016/S1352-2310(96)00277-4
CAS Web of Science® Google Scholar
Gong, R., Xu, L., Wang, D., Li, H., & Xu, J. (2016). Water quality modeling for a typical urban lake based on the EFDC model. Environmental Modeling & Assessment, 21, 643–655.
10.1007/s10666-016-9519-1
Web of Science® Google Scholar
Gong, X., Bian, J., Wang, Y., Jia, Z., & Wan, H. (2019). Evaluating and predicting the effects of land use changes on water quality using SWAT and CA–Markov models. Water Resources Management, 33, 4923–4938.
10.1007/s11269-019-02427-0
Web of Science® Google Scholar
Gough, D. I. (1969). Incremental stress under a two-dimensional artificial lake. Canadian Journal of Earth Sciences, 6(5), 1067–1075.
10.1139/e69-109
Google Scholar
Gupta, S., & Gupta, S. K. (2021). A critical review on water quality index tool: Genesis, evolution and future directions. Ecological Informatics, 63, 101299.
10.1016/j.ecoinf.2021.101299
Web of Science® Google Scholar
Hamrick, J. M. (1996). User's manual for the environmental fluid dynamics computer code. (Special Reports in Applied Marine Science and Ocean Engineering [SRAMSOE] No. 331). Virginia Institute of Marine Science, College of William and Mary. https://doi.org/10.21220/V5M74W
10.21220/V5M74W
Google Scholar
Han, M., Su, Z., & Na, X. (2023). Predict water quality using an improved deep learning method based on spatiotemporal feature correlated: A case study of the Tanghe Reservoir in China. Stochastic Environmental Research and Risk Assessment, 37(7), 2563–2575.
10.1007/s00477-023-02405-4
Web of Science® Google Scholar
Horton, R. K. (1965). An index number system for rating water quality. Journal of the Water Pollution Control Federation, 37(3), 300–306.
Google Scholar
House, M. A. (1989). A water quality index for river management. Water and Environment Journal, 3(4), 336–344.
10.1111/j.1747-6593.1989.tb01538.x
CAS Google Scholar
Ighalo, J. O., Adeniyi, A. G., & Marques, G. (2021). Artificial intelligence for surface water quality monitoring and assessment: A systematic literature analysis. Modeling Earth Systems and Environment, 7(2), 669–681.
10.1007/s40808-020-01041-z
Web of Science® Google Scholar
Kadam, A. K., Wagh, V. M., Muley, A. A., Umrikar, B. N., & Sankhua, R. N. (2019). Prediction of water quality index using artificial neural network and multiple linear regression modelling approach in Shivganga River basin, India. Modeling Earth Systems and Environment, 5, 951–962.
10.1007/s40808-019-00581-3
Google Scholar
Khullar, S., & Singh, N. (2022). Water quality assessment of a river using deep learning Bi-LSTM methodology: Forecasting and validation. Environmental Science and Pollution Research, 29(9), 12875–12889.
10.1007/s11356-021-13875-w
CAS PubMed Web of Science® Google Scholar
Kim, J., Lee, T., & Seo, D. (2017). Algal bloom prediction of the lower Han River, Korea using the EFDC hydrodynamic and water quality model. Ecological Modelling, 366, 27–36.
10.1016/j.ecolmodel.2017.10.015
Web of Science® Google Scholar
Kim, J., Seo, D., Jang, M., & Kim, J. (2021). Augmentation of limited input data using an artificial neural network method to improve the accuracy of water quality modeling in a large lake. Journal of Hydrology, 602, 126817.
10.1016/j.jhydrol.2021.126817
CAS Web of Science® Google Scholar
Koçer, M. A. T., & Sevgili, H. (2014). Parameters selection for water quality index in the assessment of the environmental impacts of land-based trout farms. Ecological Indicators, 36, 672–681.
10.1016/j.ecolind.2013.09.034
CAS Web of Science® Google Scholar
Lee, J., Woo, S. Y., Kim, Y. W., Kim, S. J., Pyo, J., & Cho, K. H. (2022). Dynamic calibration of phytoplankton blooms using the modified SWAT model. Journal of Cleaner Production, 343, 131005.
10.1016/j.jclepro.2022.131005
CAS Web of Science® Google Scholar
Lee, S., Kim, D., McCarty, G. W., Anderson, M., Gao, F., Lei, F., Moglen, G. E., Zhang, X., Yen, H., Qi, J., Crow, W., Yeo, I. Y., & Sun, L. (2024). Spatial calibration and uncertainty reduction of the SWAT model using multiple remotely sensed data. Heliyon, 10(10), e30923.
10.1016/j.heliyon.2024.e30923
PubMed Web of Science® Google Scholar
Li, L., Jiang, P., Xu, H., Lin, G., Guo, D., & Wu, H. (2019). Water quality prediction based on recurrent neural network and improved evidence theory: A case study of Qiantang River, China. Environmental Science and Pollution Research, 26, 19879–19896.
10.1007/s11356-019-05116-y
PubMed Web of Science® Google Scholar
Liou, S. M., Lo, S. L., & Wang, S. H. (2004). A generalized water quality index for Taiwan. Environmental Monitoring and Assessment, 96, 35–52.
10.1023/B:EMAS.0000031715.83752.a1
CAS PubMed Web of Science® Google Scholar
Lkr, A., Singh, M. R., & Puro, N. (2020). Assessment of water quality status of Doyang river, Nagaland, India, using water quality index. Applied Water Science, 10(1), 46.
10.1007/s13201-019-1133-3
CAS Web of Science® Google Scholar
Lombardo, A., Franco, A., Pivato, A., & Barausse, A. (2015). Food web modeling of a river ecosystem for risk assessment of down-the-drain chemicals: A case study with AQUATOX. Science of the Total Environment, 508, 214–227.
10.1016/j.scitotenv.2014.11.038
CAS PubMed Web of Science® Google Scholar
Ma, K., Lu, Y., Zhang, Y., & Zhang, Y. (2024). Trend of PFAS concentrations and prediction of potential risks in Taihu Lake of China by AQUATOX. Environmental Research, 251, 118707.
10.1016/j.envres.2024.118707
CAS PubMed Web of Science® Google Scholar
Martin, J. L., & Wool, T. A. (2017). Supplement to Water Analysis Simulation Program User Documentation, Wasp Sediment Diagenesis Routines: Model Theory and User's Guide. U.S. EPA, Region 4 Water Management Division.
Google Scholar
Masoumi, F., Najjar-Ghabel, S., & Salimi, N. (2021). Automatic calibration of the two-dimensional hydrodynamic and water quality model using sequential uncertainty fitting approach. Environmental Monitoring and Assessment, 193, 67.
10.1007/s10661-020-08831-z
CAS PubMed Web of Science® Google Scholar
Mbuh, M. J., Mbih, R., & Wendi, C. (2019). Water quality modeling and sensitivity analysis using Water Quality Analysis Simulation Program (WASP) in the Shenandoah River watershed. Physical Geography, 40(2), 127–148.
10.1080/02723646.2018.1507339
Web of Science® Google Scholar
Misaghi, F., Delgosha, F., Razzaghmanesh, M., & Myers, B. (2017). Introducing a water quality index for assessing water for irrigation purposes: A case study of the Ghezel Ozan River. Science of the Total Environment, 589, 107–116.
10.1016/j.scitotenv.2017.02.226
CAS PubMed Web of Science® Google Scholar
Mishra, A. P., Singh, S., Jani, M., Singh, K. A., Pande, C. B., & Varade, A. M. (2024). Assessment of water quality index using Analytic Hierarchy Process (AHP) and GIS: A case study of a struggling Asan River. International Journal of Environmental Analytical Chemistry, 104(5), 1159–1171.
10.1080/03067319.2022.2032015
CAS Web of Science® Google Scholar
Mokarram, M., Pourghasemi, H. R., & Pham, T. M. (2024). Enhancing water quality monitoring through the integration of deep learning neural networks and fuzzy method. Marine Pollution Bulletin, 206, 116698.
10.1016/j.marpolbul.2024.116698
CAS PubMed Web of Science® Google Scholar
Morselli, L., Olivieri, P., Brusori, B., & Passarini, F. (2003). Soluble and insoluble fractions of heavy metals in wet and dry atmospheric depositions in Bologna, Italy. Environmental Pollution, 124(3), 457–469.
10.1016/S0269-7491(03)00013-7
CAS PubMed Web of Science® Google Scholar
Moses, S. A., Janaki, L., Joseph, S., & Joseph, J. (2015). Water quality prediction capabilities of WASP model for a tropical lake system. Lakes & Reservoirs: Research & Management, 20(4), 285–299.
10.1111/lre.12110
CAS Google Scholar
Mourhir, A., Rachidi, T., & Karim, M. (2014). River water quality index for Morocco using a fuzzy inference system. Environmental Systems Research, 3, 21.
10.1186/s40068-014-0021-y
Google Scholar
Naik, M. R., Mahanty, B., Sahoo, S. K., Jha, V. N., & Sahoo, N. K. (2022). Assessment of groundwater geochemistry using multivariate water quality index and potential health risk in industrial belt of central Odisha, India. Environmental Pollution, 303, 119161.
10.1016/j.envpol.2022.119161
CAS PubMed Web of Science® Google Scholar
Nath Roy, B., Roy, H., Rahman, K. S., Mahmud, F., Bhuiyan, M. M. K., Hasan, M., Bhuiyan, A. A. K., Hasan, M., Mahbub, M. S., Jahedi, R. M., & Islam, M. S. (2024). Principal component analysis incorporated water quality index modeling for Dhaka-based rivers. City and Environment Interactions, 23, 100150.
10.1016/j.cacint.2024.100150
Google Scholar
Nazeer, S., Hashmi, M. Z., & Malik, R. N. (2014). Heavy metals distribution, risk assessment and water quality characterization by water quality index of the River Soan, Pakistan. Ecological Indicators, 43, 262–270.
10.1016/j.ecolind.2014.03.010
CAS Web of Science® Google Scholar
Niknam, A. R. R., Sabaghzadeh, M., Barzkar, A., & Shishebori, D. (2024). Comparing ARIMA and various deep learning models for long-term water quality index forecasting in Dez River, Iran. Environmental Science and Pollution Research, 32, 10206–10222. https://doi.org/10.1007/s11356-024-32228-x
10.1007/s11356-024-32228-x
PubMed Web of Science® Google Scholar
Nishat, M. H., Khan, M. H. R. B., Ahmed, T., Hossain, S. N., Ahsan, A., El-Sergany, M. M., Shafiquzzaman, M., Imteaz, M. A., & Alresheedi, M. T. (2025). Comparative analysis of machine learning models for predicting water quality index in Dhaka's rivers of Bangladesh. Environmental Sciences Europe, 37(1), 31.
10.1186/s12302-025-01078-w
Web of Science® Google Scholar
Njuguna, S. M., Onyango, J. A., Githaiga, K. B., Gituru, R. W., & Yan, X. (2020). Application of multivariate statistical analysis and water quality index in health risk assessment by domestic use of river water. Case study of Tana River in Kenya. Process Safety and Environmental Protection, 133, 149–158.
10.1016/j.psep.2019.11.006
CAS Web of Science® Google Scholar
Obin, N., Tao, H., Ge, F., & Liu, X. (2021). Research on water quality simulation and water environmental capacity in Lushui River based on WASP model. Water, 13(20), 2819.
10.3390/w13202819
CAS Web of Science® Google Scholar
Oni, O., & Fasakin, O. (2016). The use of water quality index method to determine the potability of surface water and groundwater in the vicinity of a municipal solid waste dumpsite in Nigeria. American Journal of Engineering Research, 5(10), 96–101.
Google Scholar
Ott, W. R. (1978). Water Quality Indices: A Survey of Indices Used in the United States. Environmental Protection Agency, Office of Research and Development, Office of Monitoring and Technical Support.
Google Scholar
Pak, H. Y., Chuah, C. J., Tan, M. L., Yong, E. L., & Snyder, S. A. (2021). A framework for assessing the adequacy of Water Quality Index–Quantifying parameter sensitivity and uncertainties in missing values distribution. Science of the Total Environment, 751, 141982.
10.1016/j.scitotenv.2020.141982
CAS PubMed Web of Science® Google Scholar
Park, R. A., Clough, J. S., & Wellman, M. C. (2008). AQUATOX: Modeling environmental fate and ecological effects in aquatic ecosystems. Ecological Modelling, 213(1), 1–15.
10.1016/j.ecolmodel.2008.01.015
CAS Web of Science® Google Scholar
Parween, S., Siddique, N. A., Mahammad Diganta, M. T., Olbert, A. I., & Uddin, M. G. (2022). Assessment of urban river water quality using modified NSF water quality index model at Siliguri city, West Bengal, India. Environmental and Sustainability Indicators, 16, 100202.
10.1016/j.indic.2022.100202
Web of Science® Google Scholar
Pesce, S. (2000). Use of water quality indices to verify the impact of Córdoba City (Argentina) on Suquı́a River. Water Research, 34(11), 2915–2926.
10.1016/S0043-1354(00)00036-1
CAS Web of Science® Google Scholar
Poor, N., Pribble, R., & Greening, H. (2001). Direct wet and dry deposition of ammonia, nitric acid, ammonium and nitrate to the Tampa Bay Estuary, FL, USA. Atmospheric Environment, 35(23), 3947–3955.
10.1016/S1352-2310(01)00180-7
CAS Web of Science® Google Scholar
Prasad, D. V. V., Venkataramana, L. Y., Kumar, P. S., Prasannamedha, G., Harshana, S., Srividya, S. J., Harrinei, K., & Indraganti, S. (2022). Analysis and prediction of water quality using deep learning and auto deep learning techniques. Science of the Total Environment, 821, 153311.
10.1016/j.scitotenv.2022.153311
CAS PubMed Web of Science® Google Scholar
Prati, L., & Richardson, Q. B. (1971). Water pollution and self-purification study on the Po River below ferrara. Water Research, 5(5), 203–212.
10.1016/0043-1354(71)90053-4
CAS Google Scholar
Rahat, S. H., Steissberg, T., Chang, W., Chen, X., Mandavya, G., Tracy, J., Wasti, A., Atreya, G., Saki, S., Bhuiyan, M. A. E., & Ray, P. (2023). Remote sensing-enabled machine learning for river water quality modeling under multidimensional uncertainty. Science of the Total Environment, 898, 165504.
10.1016/j.scitotenv.2023.165504
CAS PubMed Web of Science® Google Scholar
Rajaee, T., Khani, S., & Ravansalar, M. (2020). Artificial intelligence-based single and hybrid models for prediction of water quality in rivers: A review. Chemometrics and Intelligent Laboratory Systems, 200, 103978.
10.1016/j.chemolab.2020.103978
CAS Web of Science® Google Scholar
Rajkumar, H., Naik, P. K., & Rishi, M. S. (2022). A comprehensive water quality index based on analytical hierarchy process. Ecological Indicators, 145, 109582.
10.1016/j.ecolind.2022.109582
CAS Web of Science® Google Scholar
Ramos-Ramírez, L. Á., Guevara-Luna, M. A., Chiriví-Salomón, J. S., & Muñoz-Nieto, D. M. (2020). Simulation of Cr-III dispersion in the High Bogotá River Basin using the WASP model. Revista Facultad de Ingeniería Universidad de Antioquia, 97, 30–40.
CAS Google Scholar
Rasheed Abdul Haq, K. P., & Harigovindan, V. P. (2022). Water quality prediction for smart aquaculture using hybrid deep learning models. IEEE Access, 10, 60078–60098.
10.1109/ACCESS.2022.3180482
Web of Science® Google Scholar
Riffat, R. (2012). Fundamentals of Wastewater Treatment and Engineering. CRC Press.
Google Scholar
Sabinaya, S., Mahanty, B., Rout, P. R., Raut, S., Sahoo, S. K., Jha, V., & Sahoo, N. K. (2024). Multi-model exploration of groundwater quality and potential health risk assessment in Jajpur district, Eastern India. Environmental Geochemistry and Health, 46(2), 57.
10.1007/s10653-024-01855-1
CAS PubMed Web of Science® Google Scholar
Sahoo, M. M., Patra, K. C., & Khatua, K. K. (2015). Inference of water quality index using ANFIA and PCA. Aquatic Procedia, 4, 1099–1106.
10.1016/j.aqpro.2015.02.139
Google Scholar
Sakaa, B., Elbeltagi, A., Boudibi, S., Chaffaï, H., Islam, A. R. M. T., Kulimushi, L. C., Choudhari, P., Hani, A., Brouziyne, Y., & Wong, Y. J. (2022). Water quality index modeling using random forest and improved SMO algorithm for support vector machine in Saf-Saf river basin. Environmental Science and Pollution Research, 29(32), 48491–48508.
10.1007/s11356-022-18644-x
CAS PubMed Web of Science® Google Scholar
Saravanan, S., Singh, L., Sathiyamurthi, S., Sivakumar, V., Velusamy, S., & Shanmugamoorthy, M. (2023). Predicting phosphorus and nitrate loads by using SWAT model in Vamanapuram River Basin, Kerala, India. Environmental Monitoring and Assessment, 195(1), 186.
10.1007/s10661-022-10786-2
CAS Web of Science® Google Scholar
Schaffner, M., Bader, H. P., & Scheidegger, R. (2009). Modeling the contribution of point sources and non-point sources to Thachin River water pollution. Science of the Total Environment, 407(17), 4902–4915.
10.1016/j.scitotenv.2009.05.007
CAS PubMed Web of Science® Google Scholar
Schwarzenbach, R. P., Egli, T., Hofstetter, T. B., Von Gunten, U., & Wehrli, B. (2010). Global water pollution and human health. Annual Review of Environment and Resources, 35(1), 109–136.
10.1146/annurev-environ-100809-125342
Web of Science® Google Scholar
Seifi, A., Dehghani, M., & Singh, V. P. (2020). Uncertainty analysis of water quality index (WQI) for groundwater quality evaluation: Application of Monte-Carlo method for weight allocation. Ecological Indicators, 117, 106653.
10.1016/j.ecolind.2020.106653
CAS Web of Science® Google Scholar
Shah, K. A., & Joshi, G. S. (2017). Evaluation of water quality index for River Sabarmati, Gujarat, India. Applied Water Science, 7, 1349–1358.
10.1007/s13201-015-0318-7
CAS Google Scholar
Sharma, D., & Kansal, A. (2013). Assessment of river quality models: A review. Reviews in Environmental Science and Bio/Technology, 12, 285–311.
10.1007/s11157-012-9285-8
Web of Science® Google Scholar
Sharma, S., & Reddy, A. S. (2013). Development of water quality indices for designated best uses of surface water body. International Journal of Engineering Science and Innovative Technology, 2(5), 82–93.
Google Scholar
Shil, S., Singh, U. K., & Mehta, P. (2019). Water quality assessment of a tropical river using water quality index (WQI), multivariate statistical techniques and GIS. Applied Water Science, 9, 168.
10.1007/s13201-019-1045-2
Web of Science® Google Scholar
Shin, S., Her, Y., Muñoz-Carpena, R., & Yu, X. (2023). Quantifying the contribution of external loadings and internal hydrodynamic processes to the water quality of Lake Okeechobee. Science of the Total Environment, 883, 163713.
10.1016/j.scitotenv.2023.163713
CAS PubMed Web of Science® Google Scholar
Shoaei, S. M., Arjmandi, S. A., & Mirbagheri, S. A. (2022). Enhancing the CE-QUAL-W2 to model dissolved lead transport and transformation in dam reservoirs: A case study of Shahid Rajaei Dam reservoir, north part of Iran. Environmental Science and Pollution Research, 29(38), 57860–57872.
10.1007/s11356-022-19889-2
CAS PubMed Web of Science® Google Scholar
Smith, D. G. (1990). A better water quality indexing system for rivers and streams. Water Research, 24(10), 1237–1244.
10.1016/0043-1354(90)90047-A
CAS Web of Science® Google Scholar
Solanki, A., Agrawal, H., & Khare, K. (2015). Predictive analysis of water quality parameters using deep learning. International Journal of Computer Applications, 125(9), 29–34.
10.5120/ijca2015905874
Google Scholar
Stambuk-Giljanovic, N. (1999). Water quality evaluation by index in Dalmatia. Water Research, 33(16), 3423–3440.
10.1016/S0043-1354(99)00063-9
CAS Web of Science® Google Scholar
Streeter, H. W., & Phelps, E. B. (1925). A study of the pollution and natural purification of the Ohio River (No. 146). United States Public Health Service.
Google Scholar
Sutadian, A. D., Muttil, N., Yilmaz, A. G., & Perera, B. J. C. (2016). Development of river water quality indices—a review. Environmental Monitoring and Assessment, 188, 58.
10.1007/s10661-015-5050-0
PubMed Web of Science® Google Scholar
Sutadian, A. D., Muttil, N., Yilmaz, A. G., & Perera, B. J. C. (2018). Development of a water quality index for rivers in West Java Province, Indonesia. Ecological Indicators, 85, 966–982.
10.1016/j.ecolind.2017.11.049
CAS Web of Science® Google Scholar
Swaroop Bhargava, D. (1983). Use of water quality index for river classification and zoning of Ganga River. Environmental Pollution Series B, Chemical and Physical, 6(1), 51–67.
10.1016/0143-148X(83)90029-0
Google Scholar
Syeed, M. M. M., Hossain, M. S., Karim, M. R., Uddin, M. F., Hasan, M., & Khan, R. H. (2023). Surface water quality profiling using the water quality index, pollution index and statistical methods: A critical review. Environmental and Sustainability Indicators, 18, 100247.
10.1016/j.indic.2023.100247
Web of Science® Google Scholar
Talukdar, S., Shahfahad, S., Bera, S., Naikoo, M. W., Ramana, G. V., Mallik, S., Kumar, P. A., & Rahman, A. (2024). Optimisation and interpretation of machine and deep learning models for improved water quality management in Lake Loktak. Journal of Environmental Management, 351, 119866.
10.1016/j.jenvman.2023.119866
CAS PubMed Web of Science® Google Scholar
Thi Minh Hanh, P., Sthiannopkao, S., The Ba, D., & Kim, K. W. (2011). Development of water quality indexes to identify pollutants in Vietnam's surface water. Journal of Environmental Engineering, 137(4), 273–283.
10.1061/(ASCE)EE.1943-7870.0000314
Google Scholar
Thomas Jr., H. A. 1949). Pollution load capacity of streams. Water & Sewage Works, 96(7), 264–266.
Google Scholar
Tiwari, A. K., De Maio, M., Singh, P. K., & Mahato, M. K. (2015). Evaluation of surface water quality by using GIS and a heavy metal pollution index (HPI) model in a coal mining area, India. Bulletin of Environmental Contamination and Toxicology, 95, 304–310.
10.1007/s00128-015-1558-9
CAS PubMed Web of Science® Google Scholar
Tiwari, S., Babbar, R., & Kaur, G. (2018). Performance evaluation of two ANFIS models for predicting water quality index of River Satluj (India). Advances in Civil Engineering, 2018(1), 8971079.
10.1155/2018/8971079
Google Scholar
Tiyasha, T. M., Tung, T. M., & Yaseen, Z. M. (2020). A survey on river water quality modelling using artificial intelligence models: 2000–2020. Journal of Hydrology, 585, 124670.
10.1016/j.jhydrol.2020.124670
CAS Web of Science® Google Scholar
Tripathi, M., & Singal, S. K. (2019). Use of principal component analysis for parameter selection for development of a novel water quality index: A case study of river Ganga India. Ecological Indicators, 96, 430–436.
10.1016/j.ecolind.2018.09.025
CAS Web of Science® Google Scholar
Uddin, M. G., Jackson, A., Nash, S., Rahman, A., & Olbert, A. I. (2023). Comparison between the WFD approaches and newly developed water quality model for monitoring transitional and coastal water quality in Northern Ireland. Science of the Total Environment, 901, 165960.
10.1016/j.scitotenv.2023.165960
CAS PubMed Web of Science® Google Scholar
Uddin, M. G., Nash, S., Mahammad Diganta, M. T., Rahman, A., & Olbert, A. I. (2022). Robust machine learning algorithms for predicting coastal water quality index. Journal of Environmental Management, 321, 115923.
10.1016/j.jenvman.2022.115923
PubMed Web of Science® Google Scholar
Uddin, M. G., Nash, S., & Olbert, A. I. (2021). A review of water quality index models and their use for assessing surface water quality. Ecological Indicators, 122, 107218.
10.1016/j.ecolind.2020.107218
CAS Web of Science® Google Scholar
Uddin, M. G., Nash, S., Rahman, A., & Olbert, A. I. (2023). A sophisticated model for rating water quality. Science of the Total Environment, 868, 161614.
10.1016/j.scitotenv.2023.161614
CAS PubMed Web of Science® Google Scholar
Uddin, M. G., Rahman, A., Nash, S., Diganta, M. T. M., Sajib, A. M., Moniruzzaman, M., & Olbert, A. I. (2023). Marine waters assessment using improved water quality model incorporating machine learning approaches. Journal of Environmental Management, 344, 118368.
10.1016/j.jenvman.2023.118368
CAS PubMed Web of Science® Google Scholar
Ustaoğlu, F., Tepe, Y., & Taş, B. (2020). Assessment of stream quality and health risk in a subtropical Turkey river system: A combined approach using statistical analysis and water quality index. Ecological Indicators, 113, 105815.
10.1016/j.ecolind.2019.105815
CAS Web of Science® Google Scholar
Verma, M., Loganathan, V. A., & Bhatt, V. K. (2022). Development of entropy and deviation-based water quality index: Case of River Ganga, India. Ecological Indicators, 143, 109319.
10.1016/j.ecolind.2022.109319
CAS Web of Science® Google Scholar
Wan, H., Xu, R., Zhang, M., Cai, Y., Li, J., & Shen, X. (2022). A novel model for water quality prediction caused by non-point sources pollution based on deep learning and feature extraction methods. Journal of Hydrology, 612, 128081.
10.1016/j.jhydrol.2022.128081
CAS Web of Science® Google Scholar
Wang, Q., Li, S., Jia, P., Qi, C., & Ding, F. (2013). A review of surface water quality models. The Scientific World Journal, 2013(1), 231768.
10.1155/2013/231768
PubMed Google Scholar
Welander, P. (1968). Wind-driven circulation in one-and two-layer oceans of variable depth. Tellus, 20(1), 1–16.
10.1111/j.2153-3490.1968.tb00347.x
Google Scholar
Wepener, V., Euler, N., Van Vuren, J. H. J., Du Preez, H. H., & Kohler, A. (1992). The development of an aquatic toxicity index as a tool in the operational management of water quality in the Olifants River (Knsger National Park). Koedoe, 35(2), a400.
10.4102/koedoe.v35i2.400
Google Scholar
Woo, S. Y., Kim, S. J., Lee, J. W., Kim, S. H., & Kim, Y. W. (2021). Evaluating the impact of interbasin water transfer on water quality in the recipient river basin with SWAT. Science of the Total Environment, 776, 145984.
10.1016/j.scitotenv.2021.145984
CAS PubMed Web of Science® Google Scholar
Wool, T. A., Ambrose, R. B., Martin, J. L., Comer, E. A., & Tech, T. (2006). Water quality analysis simulation program (WASP). User's Manual. Version, 6. US EPA.
Google Scholar
Wu, Z., Lai, X., & Li, K. (2021). Water quality assessment of rivers in Lake Chaohu Basin (China) using water quality index. Ecological Indicators, 121, 107021.
10.1016/j.ecolind.2020.107021
CAS Web of Science® Google Scholar
Xu, S., He, G., Fang, H., Bai, S., & Wu, X. (2022). Parameter uncertainty and sensitivity analysis of the three Gorges Reservoir and Xiangxi River EFDC model. Journal of Hydrology, 610, 127881.
10.1016/j.jhydrol.2022.127881
CAS Web of Science® Google Scholar
Yih, S. M., & Davidson, B. (1975). Identification in nonlinear, distributed parameter water quality models. Water Resources Research, 11(5), 693–704.
10.1029/WR011i005p00693
Web of Science® Google Scholar
Yu, J. W., Kim, J. S., Li, X., Jong, Y. C., Kim, K. H., & Ryang, G. I. (2022). Water quality forecasting based on data decomposition, fuzzy clustering and deep learning neural network. Environmental Pollution, 303, 119136.
10.1016/j.envpol.2022.119136
CAS PubMed Web of Science® Google Scholar
Yu, Z., Dai, H., Yang, J., Zhu, Y., & Yuan, S. (2024). Global sensitivity analysis with deep learning-based surrogate models for unraveling key parameters and processes governing redox zonation in Riparian zone. Journal of Hydrology, 638, 131442.
10.1016/j.jhydrol.2024.131442
CAS Web of Science® Google Scholar
Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8, 338–353.
10.1016/S0019-9958(65)90241-X
CAS Web of Science® Google Scholar
Zamani, M. G., Nikoo, M. R., Jahanshahi, S., Barzegar, R., & Meydani, A. (2023). Forecasting water quality variable using deep learning and weighted averaging ensemble models. Environmental Science and Pollution Research, 30(59), 124316–124340.
10.1007/s11356-023-30774-4
PubMed Web of Science® Google Scholar
Zeiger, S. J., & Hubbart, J. A. (2016). A SWAT model validation of nested-scale contemporaneous stream flow, suspended sediment and nutrients from a multiple-land-use watershed of the central USA. Science of the Total Environment, 572, 232–243.
10.1016/j.scitotenv.2016.07.178
CAS PubMed Web of Science® Google Scholar
Zeinalzadeh, K., & Rezaei, E. (2017). Determining spatial and temporal changes of surface water quality using principal component analysis. Journal of Hydrology: Regional Studies, 13, 1–10.
10.1016/j.ejrh.2017.07.002
Web of Science® Google Scholar
Zhang, L., Cui, J., Song, T., & Liu, Y. (2018). Application of an AQUATOX model for direct toxic effects and indirect ecological effects assessment of polycyclic aromatic hydrocarbons (PAHs) in a plateau eutrophication lake, China. Ecological Modelling, 388, 31–44.
10.1016/j.ecolmodel.2018.09.019
CAS Web of Science® Google Scholar
Zhang, L., & Liu, J. (2014). AQUATOX coupled foodweb model for ecosystem risk assessment of polybrominated diphenyl ethers (PBDEs) in lake ecosystems. Environmental Pollution, 191, 80–92.
10.1016/j.envpol.2014.04.013
CAS PubMed Web of Science® Google Scholar
Zhang, P., Liu, R., Bao, Y., Wang, J., Yu, W., & Shen, Z. (2014). Uncertainty of SWAT model At different DEM resolutions In a large mountainous watershed. Water Research, 53, 132–144.
10.1016/j.watres.2014.01.018
CAS PubMed Web of Science® Google Scholar
Zhang, Y., Xia, J., Shao, Q., & Zhai, X. (2013). Water quantity and quality simulation by improved SWAT in highly regulated Huai River Basin of China. Stochastic Environmental Research and Risk Assessment, 27, 11–27.
10.1007/s00477-011-0546-9
CAS Web of Science® Google Scholar
Zhang, Z., Sun, B., & Johnson, B. E. (2015). Integration of a benthic sediment diagenesis module into the two dimensional hydrodynamic and water quality model–CE-QUAL-W2. Ecological Modelling, 297, 213–231.
10.1016/j.ecolmodel.2014.10.025
CAS Web of Science® Google Scholar
Zheng, H., Liu, Y., Wan, W., Zhao, J., & Xie, G. (2023). Large-scale prediction of stream water quality using an interpretable deep learning approach. Journal of Environmental Management, 331, 117309.
10.1016/j.jenvman.2023.117309
CAS PubMed Web of Science® Google Scholar
Zhi, W., Feng, D., Tsai, W. P., Sterle, G., Harpold, A., Shen, C., & Li, L. (2021). From hydrometeorology to river water quality: Can a deep learning model predict dissolved oxygen at the continental scale? Environmental Science & Technology, 55(4), 2357–2368.
10.1021/acs.est.0c06783
CAS PubMed Google Scholar
Zhi, W., Ouyang, W., Shen, C., & Li, L. (2023). Temperature outweighs light and flow as the predominant driver of dissolved oxygen in US Rivers. Nature Water, 1(3), 249–260.
10.1038/s44221-023-00038-z
CAS Web of Science® Google Scholar
Zhou, Y. (2020). Real-time probabilistic forecasting of river water quality under data missing situation: Deep learning plus post-processing techniques. Journal of Hydrology, 589, 125164.
10.1016/j.jhydrol.2020.125164
Web of Science® Google Scholar

Volume4, Issue2

May 2025

Pages 265-286

Perspectives on water quality analysis emphasizing indexing, modeling, and application of artificial intelligence for comparison and trend forecasting

Abstract

1 INTRODUCTION